露天矿爆破时砖混结构房屋振动响应的模态参数识别与爆破减振方法❋

张国胜 郭 斌 刘永亮 张云鹏 杨 曦

①河北钢铁集团矿业有限公司(河北唐山，063000)

②华北理工大学河北省矿业开发与安全技术重点实验室(河北唐山，063000)

引言

近些年来，随着矿山行业的发展，矿石开采过程中的爆破振动对周围环境的影响也逐渐被社会关注。尤其是爆破过程中产生的爆破地震波，会引起矿山周围建筑物的振动，如果其强度超过一定阈值，就会造成矿山周围建筑物不同程度的破坏[1-3]。对爆破地震波产生的振动效应进行系统研究的工作一直在进行，研究对象众多[4-8]。但是，矿区周围村镇较多，建筑主体多以单层砖混结构房屋为主，而目前针对单层砖混结构房屋地基与墙壁振动响应的研究还相对较少，急需开展相应的研究。

爆破振动信号为非常典型的非平稳信号[9]。朱权洁等[10]充分利用小波包技术，分析了矿山生产产生的爆破信号，并与岩石破裂产生的信号进行了对比，确定了其各自的能量频带分布特征。龚敏等[11]对隧道开采过程中的爆破振动信号进行了采集，运用希尔伯特黄变换(Hilbert Huang transform，HHT)和经验模态分解(empirical mode decomposition，EMD)对不同雷管延期时间的瞬时能量进行了分析。赵国彦等[12]采用频率切片小波变换(frequency slice wavelet transform，FSWT)对岩体微振和爆破振动信号在不同频域的能量比例进行了研究。Triviño等[13]对不同爆破条件下的爆破地震波进行分析，确定了其能量和频率的变化规律。

针对矿区周边的单层砖混结构房屋的地基与墙壁，根据运筹模态分析(operational modal analysis，OMA)理论，对采集到的爆破地震波信号，运用HHT和小波包分解的方法，获取其模态参数，分析爆破地震波不同频段的贡献率，并确定其频域能量特征。提出了爆破减振方法，并进行了数值模拟验证。

1 工程概况与监测方法

某矿露天生产爆破时，对采场附近单层砖混结构房屋进行监测，获取振动响应信号数据。监测点距离爆区820 m。

露天生产爆破采用逐孔起爆技术。台阶高度14.0～15.5 m；炮孔直径310 mm；孔深16.0～17.5 m(超深2.0 m，填塞长度7.0～7.5 m)；矿石孔网参数(7～8)m×(6～7)m；岩石孔网参数(5～9)m×(4～8)m；使用的炸药为铵油、乳化炸药；矿石炸药单耗为0.45～1.00 kg/m3；岩石炸药单耗为0.40～0.45 kg/m3。

使用中科院TC-4850型爆破测振仪，主要监测单层砖混结构房屋的墙壁与地基的爆破振动情况。地基测点为B6。墙壁各测点分别为B2、B3和B4，各个测点之间的距离为80 cm，如图1所示。

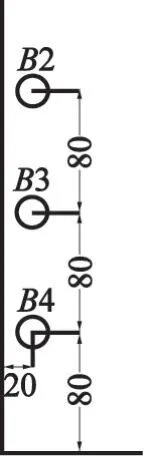
图1 墙壁测点(单位:cm)Fig.1 Measuring points on the wall(unit:cm)

2 爆破振动信号分析

2.1 爆破振动影响下地基模态参数计算

根据现场爆破振动监测结果，得到房屋地基X、Y、Z3个方向的振速时程信号。分别对这3个方向的振速时程信号进行EMD处理，就可以得到不同的数据序列，每个序列称为固有模态函数(instrinsic mode function，IMF)，然后分别对IMF进行HHT处理，得到相应信号在11阶固有模态下的分解信号。以地基在Y方向的爆破振动信号为例，结果见图2。

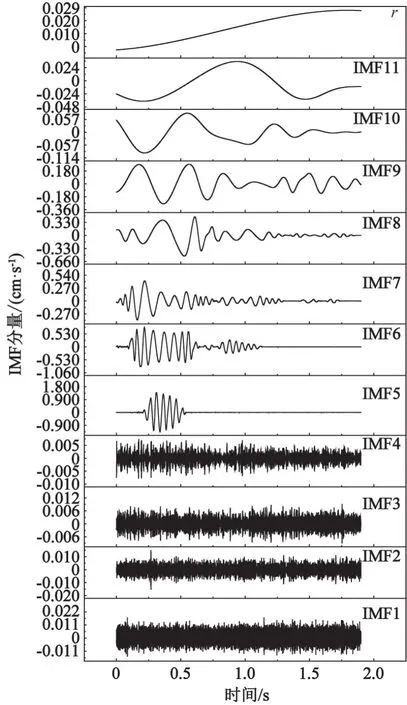
图2 地基测点Y方向爆破振动信号的IMF分量和剩余分量rFig.2 IMF component and residual component r of blasting vibration signal in Y direction of measuring point on ground foundation

然后，进行方差贡献率分析，得到房屋地基X、Y、Z3个方向的IMF贡献率，如图3所示。观察可知:3个方向的信号在5、6阶的IMF贡献率均较高；其中，第5阶的IMF贡献率略高；7、8、9阶次之；其他序列IMF贡献率过低，可忽略不计。

图3 地基测点IMF分量的贡献率Fig.3 Contribution rate of IMF component of measuring point on ground foundation

对Y方向各个序列的振速时程信号分别进行10层小波包分解，得到其归一化能量谱图，分析后可得其各阶固有频率，如图4所示。由此可知，3个方向的信号在54.67 Hz的IMF贡献率较高。

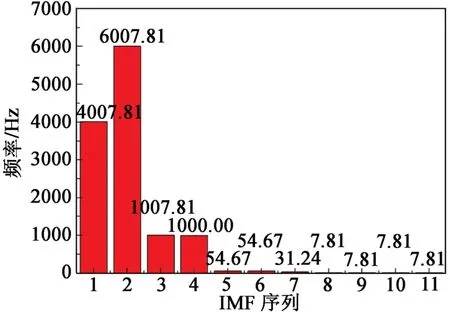
图4 IMF1～IMF11各阶的固有频率Fig.4 Natural frequencies of IMF1-IMF11

2.2 爆破振动影响下墙壁模态参数计算

在开展地基爆破振动信号监测的同时，在墙壁进行钻孔，安装膨胀螺栓，再用固定架套住探头，并将其固定在膨胀螺栓上，对墙壁各个测点也开展相应的监测工作。得到单层砖混结构房屋墙壁各个测点X、Y、Z3个方向的振速时程信号。分别对3个方向的振速时程信号进行EMD处理，就可以得到相应信号在10阶固有模态下的分解信号。B2测点在Y方向的爆破振动信号处理结果如图5所示。

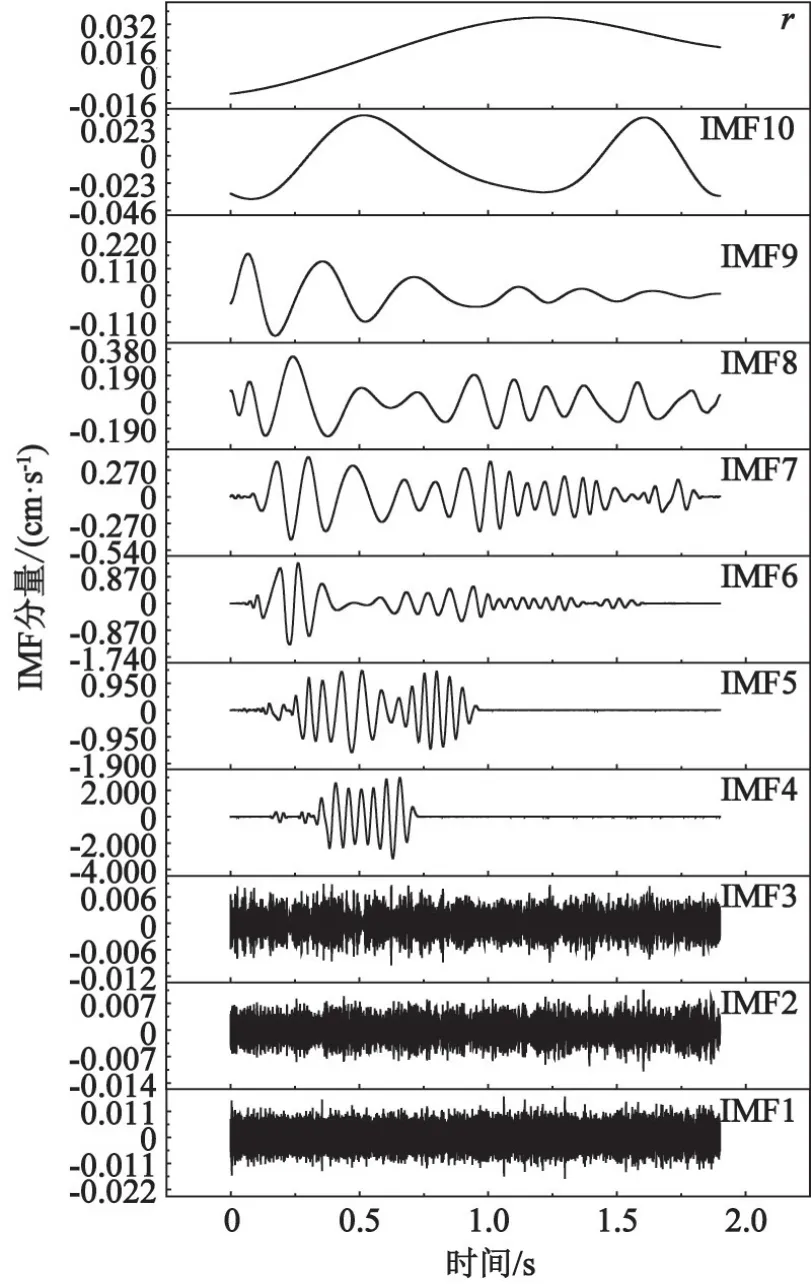
图5 墙壁B2测点Y方向的爆破振动信号的IMF分量和剩余分量rFig.5 IMF component and residual component r of blasting vibration signal in Y direction of Measuring Point B2 on the wall

根据现场爆破振动监测与上述计算结果，进行方差贡献率分析，得到单层砖混结构房屋墙壁B2测点X、Y、Z3个方向的IMF贡献率，如图6所示。观察可知，3个方向信号的主导IMF贡献率并不相同。X方向，6阶IMF贡献率最高；Y方向，4阶IMF贡献率最高；Z方向，5阶IMF贡献率最高。与地基各阶IMF贡献率相比，存在明显差异。这说明单层砖混结构房屋墙壁的动力响应与地基的动力响应相比，其起主导作用的振动频率并不相同。

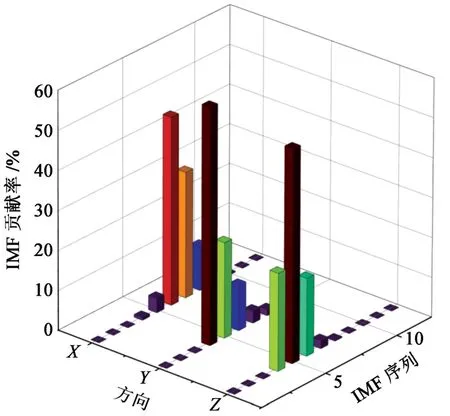
图6 墙壁B2测点IMF分量的贡献率Fig.6 Contribution rate of IMF component of Measuring Point B2 on the wall

对单层砖混结构房屋墙壁B2测点Y方向各个序列的振速时程信号分别进行10层小波包分解，得到其归一化能量谱图，分析后可得其各阶固有频率，如图7所示。X方向，在23.43 Hz的IMF贡献率最高；Y方向，在54.67 Hz的IMF贡献率最高；Z方向，在23.43 Hz的IMF贡献率最高。

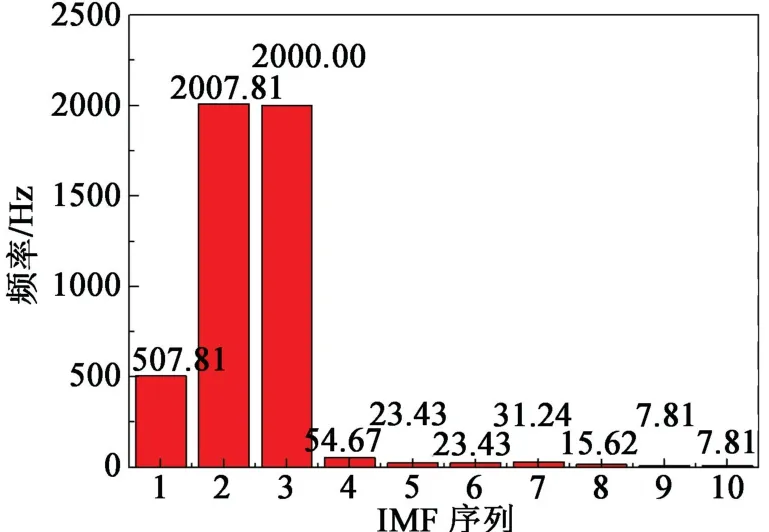
图7 IMF1～IMF10各阶的固有频率Fig.7 Natural frequencies of IMF1-IMF10

2.3 爆破振动作用下频域能量分析

为进一步分析不同位置的频域能量变化规律，对各个测点Y方向的爆破振动信号进行降噪处理后，进行db8小波包分解，得到其归一化能量分布图，如图8所示。每个频段的大小为7.81 Hz。

观察图8可知，各个测点的能量分布主要集中7.81～31.24 Hz(低)、46.86～62.48 Hz(高)两个频段范围内，其中，各个测点受高频成分影响较大。其中，低频段以15.62～23.43 Hz为主；高频段以54.67～62.48 Hz为主。观察B2、B3、B4测点可知:随着墙壁高度的增加，在低频段，低频能量逐渐减小；在高频段，高频能量逐渐增加。

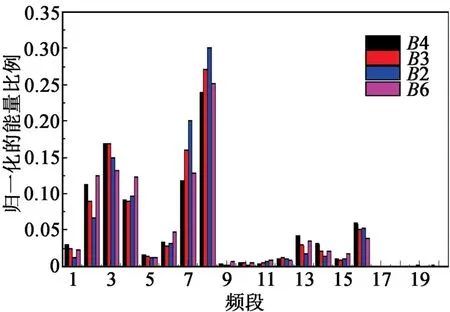
图8 地基与墙壁各测点在不同频段的归一化能量分布Fig.8 Normalized energy distribution of measuring points on foundation and wall

目前，国内多以GB6722—2014《爆破安全规程》为依据，对爆破地震波是否对房屋安全产生不利影响进行判定。其中，采用保护对象所在地质点峰值振动速度和主振频率为主要依据。但是，从上述分析结果中可以看出:随着高度的增加，墙壁上测点高频段能量逐渐增大，并超过地基高频段的能量；低频段的能量逐渐减小。当墙壁测点高、低频段能量均高于地基在高、低频段的能量，或其总和高于地基在高、低频段的能量的总和，那么，只以所在地质点的振速和主频为依据，判别房屋的稳定性，可能会产生一定的误差。同时，房屋是由不同结构组成的，由于其固有频率的影响，对爆破地震波中的不同频率成分的敏感性也不相同。故不同结构对爆破地震波会产生不同的响应，并带来不同的损伤，这还需要作进一步的研究。

3 爆破减振技术

应用数码电子雷管可以利用合理的延期起爆时间和装药结构，使不同的爆破地震波波形峰谷叠加，进而达到减小爆破振动效应的目的。

应用Ls-DYNA建立数值模型，如图9所示。模型长100 m、高24 m。模拟时间50 000μs。炸药与岩石采用的材料模型分别为Mat＿High＿Explosive＿Burn和Mat＿Plastic＿Kinematic。采用JWL状态方程。根据矿山实际，并参考前人经验，确定状态方程参数如表1所示；岩石材料的力学参数见表2。

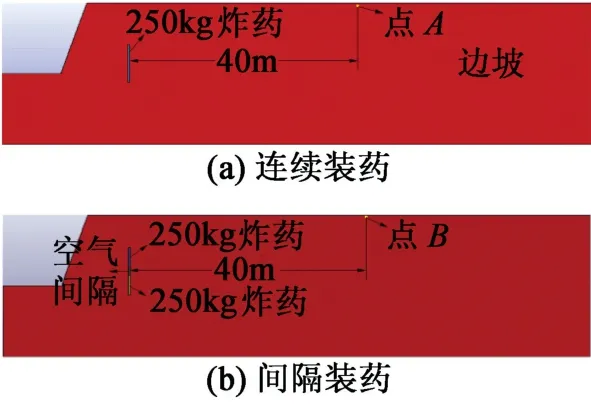
图9 装药模型Fig.9 Charge model

表1 状态方程参数Tab.1 State equation parameters

提取A点的爆破振速(图10)，最大值达到100 cm/s。但是，如果采用如图9(b)所示的间隔装药方式，通过合理控制延期起爆时间，使两个药包间隔半个周期(400μs)起爆，就可以使两个药包附近位置的波形产生峰谷叠加效应(图11)，进而达到减小爆破振动效应的目的。同时，起爆的总药量没有改变，但在相同距离上，B点的质点振速峰值为90 cm/s(图12)，较原来减小了10%。

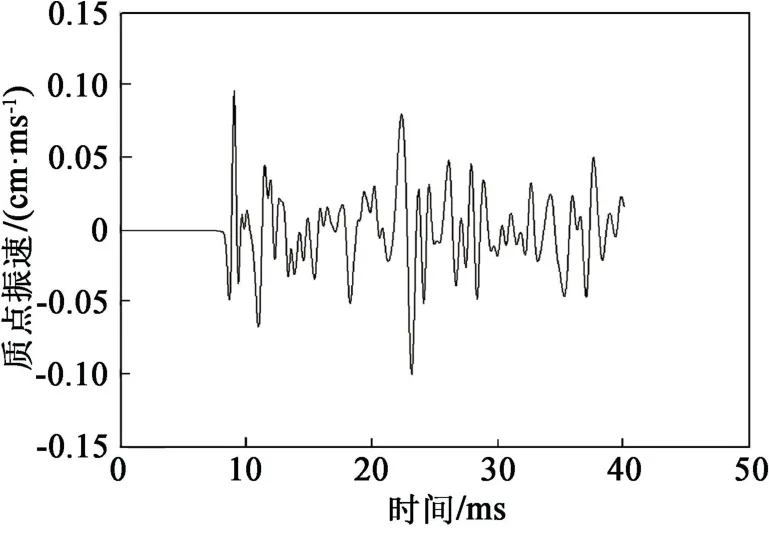
图10 连续装药A点的质点振速Fig.10 Particle vibration velocity of Point A in continuous charge

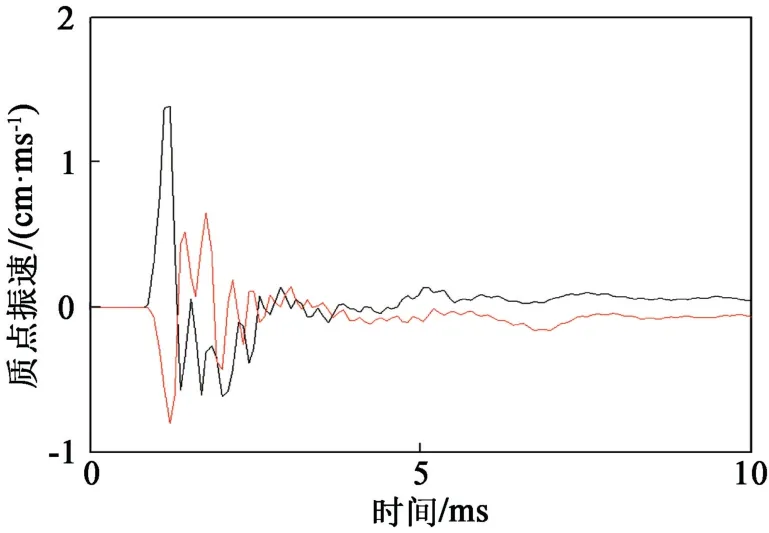
图11 峰谷叠加效应Fig.11 Peak-valley superposition effect

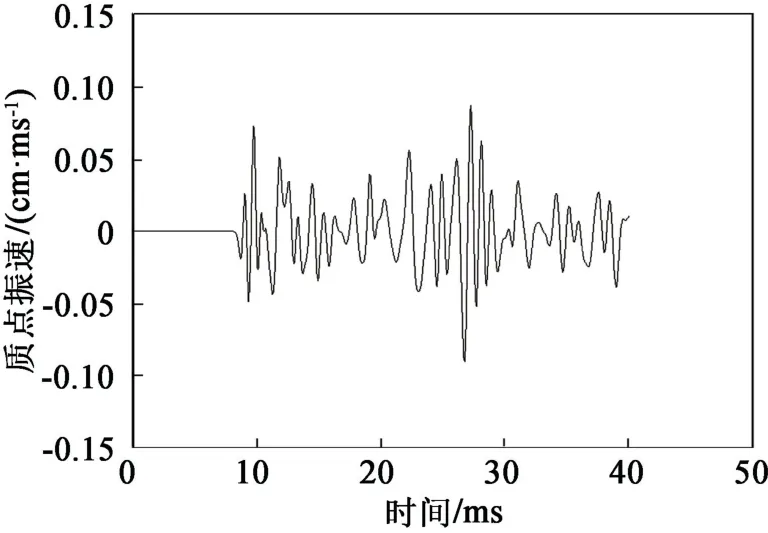
图12 叠加后B点的质点振速Fig.12 Particle vibration velocity of Point B after superposition

为进一步验证方法的可行性，建立单层砖混结构房屋数值模型(图13)。首先，将采集到的地震波施加于模型底面，并采集房屋地表与墙壁振动数据。然后，在模型底面分区域间隔半个周期，分别施加地震波，并采集房屋地表与墙壁振动数据。结果如表3所示。叠加后振速明显小于叠加前振速，进一步确定了模拟的准确性。

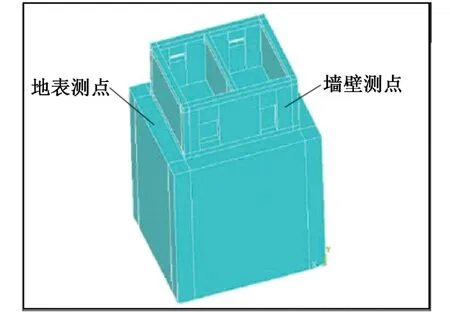
图13 单层砖混结构房屋数值模型Fig.13 Numerical model of the single-layer brick-concrete building

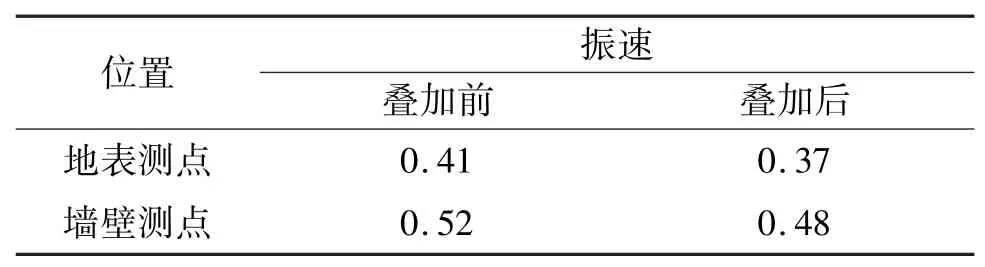
表3 叠加前、后不同位置的振速Tab.3 Vibration velocity of different points before and after superposition cm/s

4 结论

通过对矿区周围单层砖混结构房屋爆破振动信号的采集，根据OMA方法相关理论，对采集到的爆破地震波信号，运用HHT和小波包分解的方法对其进行分析，得出以下结论:

1)确定了单层砖混结构房屋地基与墙壁爆破振动信号的各阶固有频率和不同振动方向各阶的IMF贡献率，地基与墙壁的IMF贡献率存在明显差异，地基高频序列(54.67 Hz)的IMF贡献率较高，墙壁低频序列(23.43 Hz)的IMF贡献率较高。

2)墙壁各个测点的能量分布主要集中7.81～31.24 Hz(低)、46.86～62.48 Hz(高)两个频段范围内，各个测点受高频成分影响较大。其中，低频段以15.62～23.43 Hz为主，高频段以54.67～62.48 Hz为主。随着墙壁高度的增加，在低频段，低频能量逐渐减小；在高频段，高频能量逐渐增加。不同位置处的能量并不相同。

3)通过分段装药与半周期延时起爆，使爆破地震波出现峰谷叠加现象，可以减小爆破振动效应，降低质点振速。