CEEMDAN-小波包联合降噪的优化方法❋
2021-07-14王海龙王晟华
王海龙 李 帅 赵 岩 王晟华
①河北建筑工程学院土木工程学院(河北张家口,075000)
②中国矿业大学(北京)力学与建筑工程学院(北京,100083)
③北旺集团有限公司(河北承德,067400)
引言
隧道爆破振动信号降噪处理是对后续信号分析所做的重要准备工作。爆破现场工况复杂,爆破振动信号受工况影响含噪严重;因此,需要一种精确、高效的信号降噪算法。国内外学者对信号降噪的研究已经开展许久,目前,较常见的信号降噪方法有小波变换(wavelet transform,WT)[1]、经验模态分解(empirical mode decomposition,EMD)[2]、集合经验模态分解(ensemble empirical mode decomposition,EEMD)[3]、互补集合经验模态分解(complete ensemble empirical mode decomposition,CEEMD)[4]和基于自适应噪声的完备经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)[5]等。其中,EMD方法会导致部分模态混叠;EEMD和CEEMD方法通过加入高斯白噪声,使原始信号时频空间分割成不同尺度成分,但分解结果难免受到残余噪声的影响;CEEMDAN方法通过自适应加入白噪声,克服了重构误差发生的问题,但仍无法避免残余噪声的影响[6-7]。因为小波变换在处理信号高频部分时效果较差,所以在小波变换的基础上衍生出了小波包变换[8],既可以对低频部分进行分解,又能更好地处理信号的高频部分。虽然小波包变换提高了信号的时频分辨率,但无法改善信号边缘模糊等失真现象。
本文中,针对CEEMDAN-小波包联合降噪方法存在的不足,引入多尺度排列熵(MPE)概念,筛选经CEEMDAN处理得到的噪声明显的本征模态分量,通过小波包对筛选的模态分量进行降噪处理;再对未处理的分量和处理后的信号进行重构,利用SG(savitzky-golay)平滑滤波方法进一步降低残余噪声;通过仿真信号验证并应用于太锡铁路太崇段崇礼隧道3#斜井监测得到的爆破信号降噪分析中。
1 基本理论
1.1 CEEMDAN-小波包联合降噪原理
CEEMDAN方法基于EMD分解,通过添加自适应白噪声和计算唯一的余量信号来执行;小波包方法基于小波变换,对小波变换处理不好的高频部分进行细化分解。二者联合算法既可以提高CEEMDAN算法的分解精度,更好地保存原信号中的特征信息,又能够降低残余高斯白噪声的影响,同时具有两者的优点。
联合算法将爆破振动信号进行不同尺度的分解,通过计算分解所得本征模态分量的相关系数,筛选出噪声明显的本征模态分量;最后,使用小波包方法对筛选出的本征模态分量进一步分解降噪。经上述过程处理过的信号被视为纯净信号,具体计算步骤如下[9-10]。
1)定义E k(·)为EMD分解生成的第k个模态分量,由CEEMDAN分解得到的第k个模态分量记为为满足标准正态分布的高斯白噪声,ε为高斯白噪声的标准差。
2)对信号x(t)+ε0vi(t)进行I次实验,通过EMD分解获取第1个模态分量
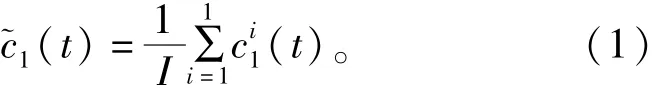
3)在第一阶段(k=1),计算第1个唯一的余量信号
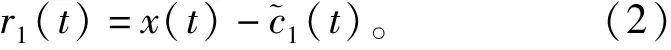
4)进行第i次实验(i=1,2,3,…,I),每次实验中,对信号r i(t)=ε1E1[v i(t)]进行分解,直到获得第1个模态分量为止,开始计算第2个模态分量

5)其余各个阶段(即k=2,3,4,…,K),与式(2)、式(3)计算过程一致,首先计算第k个余量信号,再计算第k+1个模态分量。
6)重复进行式(4)、式(5)的计算过程,直到余量信号的极点少于2。此时,所有模态函数的数量为K,最终余量满足
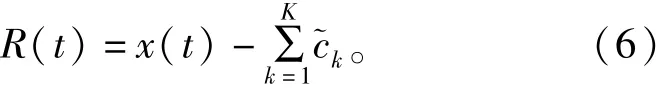
原信号序列x(t)被分解为
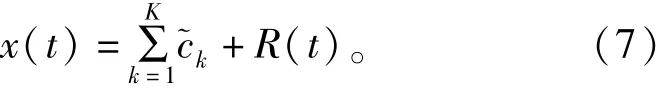
7)计算每个分量与原始信号的相关系数,并计算方差贡献率(MMSE)来校核上述选择的合理性。
8)通过步骤(7)筛选出来的含有噪声的模态分量进行小波包降噪。
9)重构经过处理和未经处理的本征模态分量,视为纯净信号。
1.2 多尺度排列熵和SG平滑滤波原理
多尺度排列熵定义为时间序列进行多尺度粒化后的排列熵,可以用来衡量时间序列在不同尺度下的复杂性和随机性,其过程是对原始时间序列进行粗粒化处理,构造出多尺度时间序列,然后计算各尺度下的排列熵。排列熵越小,时间序列越规则;排列熵越大,时间序列越复杂。从而精确筛选出含噪分量。对于某一时间序列X={x(i),i=1,2,3,…,n}(n为采样点个数),其具体步骤如下[9,11-12]。
1)对时间序列X={x(i),i=1,2,3,…,n}进行粗粒化处理,得到处理后的粗粒化序列

式中:s为尺度因子;y s(j)为不同尺度因子下的时间序列。
2)对时间序列y s(j)进行重构,
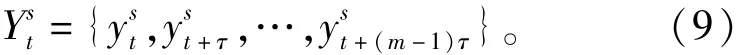
式中:m为嵌入维数;t为延迟时间。
3)计算尺度因子s下该时间序列的排列熵
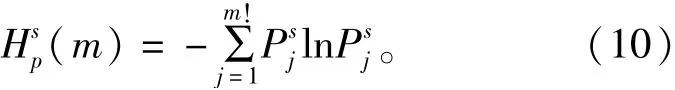
式中:P j为第j次符号序列出现的概率。
SG平滑滤波基于曲线局部特征的多项式拟合,是应用最小二乘法确定加权系数进行移动窗口加权平均的滤波方法,重构的数据能够较好地保留局部特征[13]。
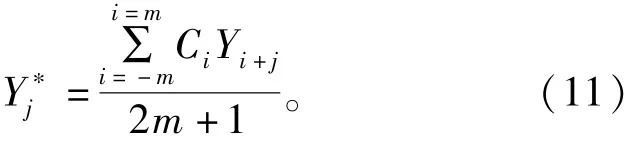
式中:Y是原始时间序列;Y∗是新得到的时间序列;C i是该滑动窗口的第i个时间序列的相关系数;2m+1为滑动窗口的大小。
1.3 CEEMDAN-小波包联合算法的优化
随机检测分解后的各本征模态分量的多尺度排列熵,经多次实验,将熵大于0.5的分量重组并进行小波包降噪处理,虽然可以去除大多数噪声,但仍不可避免残余噪声的影响;因此,将降噪后的分量与剩余分量重组,并对重组后的信号进行SG平滑滤波处理,将局部强干扰剔除。经过优化后的CEEMDAN-小波包联合算法不但排除了CEEMDAN分解方法中残余噪声的影响,而且进一步增强了小波包降噪的精度。
2 仿真信号分析
为进一步验证CEEMDAN-小波包联合降噪方法的有效性,使用仿真信号进行模拟。
构筑仿真信号如下:
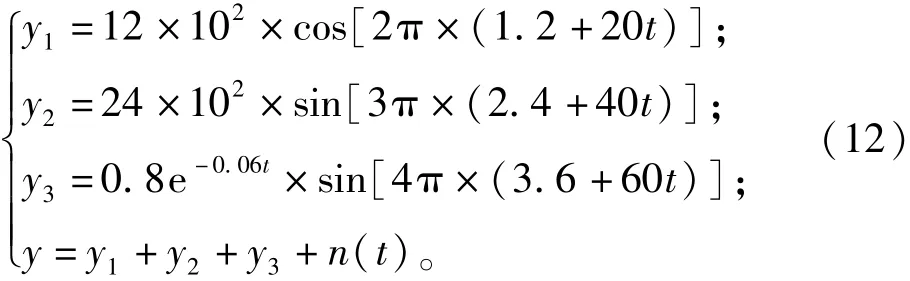
式中:t=[0,2],时间步长0.001 s,n(t)为添加周期噪声信号。
仿真信号模态分量分解结果如图1。
对每一个本征模态分量进行多尺度排列熵计算,结果见表1。对于不同信号、不同信噪比,存在一个降噪效果最好的分解尺度。如果分解尺度过大,将造成信号信息丢失严重,降噪后信噪比反而会下降;分解尺度过小的话,信噪比提高不明显,降噪效果差。经多次试错,将熵大于0.5对应的本征模态分量重构,然后通过小波包进行4层分解,选择具有良好的紧支撑性、光滑性以及近似对称性的db8小波基[14],通过小波包方法降噪,将降噪后的分量与剩余本征模态分量重组,使用SG平滑滤波进一步处理,得到降噪后的信号,如图2所示。
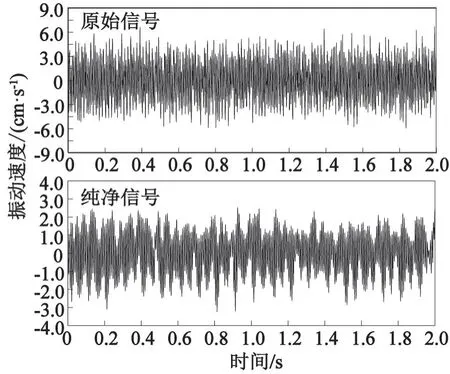
图2 原始信号及降噪后的信号Fig.2 Original signal and signal after noise reduction
对比可知,纯净信号在剔除噪声信号的基础上最大限度地保留了原始信号的特征信息,且进一步减少了信号中的毛刺和不平滑现象。
用EMD-小波包、EEMD-小波包、CEEMD-小波包、CEEMDAN-小波包4种常见的联合降噪方法对仿真信号进行处理,计算降噪后的纯净信号和原始信号的相关系数,结合降噪信号的信噪比(SNR)和均方根差(RMSE)进行综合比较。信噪比越大,均方根差越小,则表示降噪效果越好。
比较结果见表2。
比较结果显示,本优化方法的降噪效果优于其他几种与小波包联合的降噪方法。
3 实测爆破振动信号分析
3.1 工程背景
本文中,以新建太锡铁路太崇段崇礼隧道3#斜井正洞爆破为例,对实测爆破振动信号去噪并分析。3#斜井正洞洞身主要穿越早远古代变质岩系红旗营子群斜长片麻岩,弱风化,节理裂隙发育,岩体较完整,围岩稳定性为一般~较差。爆破振动信号采集于3#斜井正洞小里程钻爆法施工。
3.2 爆破振动信号采集
本次爆破振动信号采集使用中科测控公司研发的TC-4850N爆破测振仪,所采集爆破振动数据使用4850N Software分析软件进行初步分析。用不锈钢夹片将振动传感器固定于隧道内线路行进方向右侧约1.5 m的高度处,如图3。

图3 测点布置Fig.3 Layout of measuring points
图4为隧道内某次爆破施工采集到的爆破振动信号Z轴上的波形图。由于施工现场存在各种噪声源,波形图中夹杂着与爆破振动无关的噪声干扰信号。
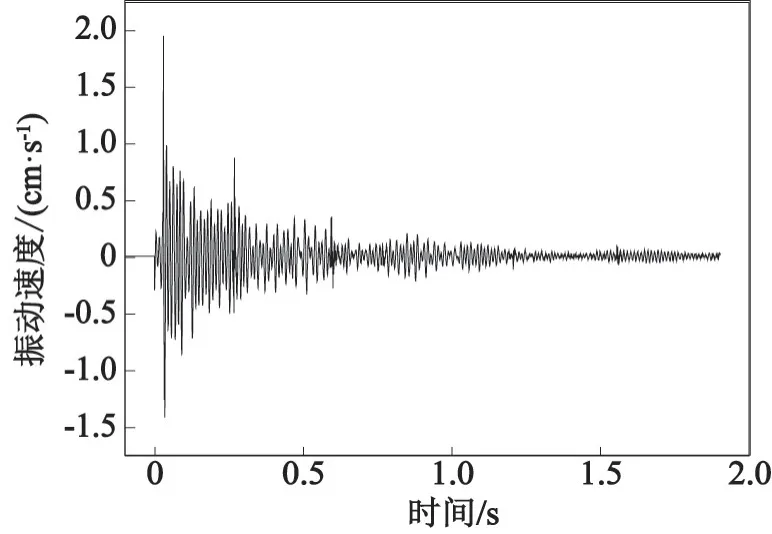
图4 隧道爆破振动信号波形Fig.4 Waveform of vibration signal in tunnel blasting
3.3 使用优化方法降噪
分别计算原始爆破信号分解出的15个本征模态分量的多尺度排列熵(表3)。表3中,将C1~C6、C11~C13、C15这10个熵大于0.5的分量重构进行小波包降噪,把降噪后的信号C16与C7~C10、C14重构后,进行SG平滑滤波处理,得到降噪后的信号,如图5所示。
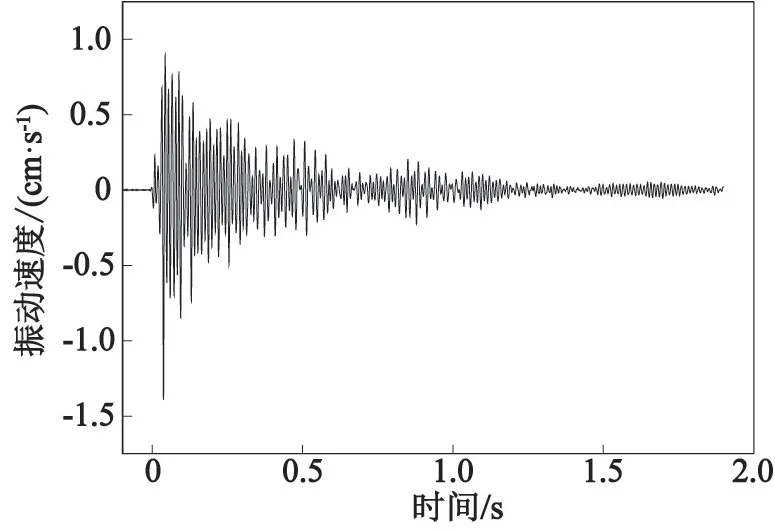
图5 降噪处理后的实测信号Fig.5 Measured signal after noise reduction

表3 实测信号模态分量熵Tab.3 Modal component entropy of measured signal
3.4 优化方法的降噪效果评价
图6为用的其他4种方法对本文中的实测信号降噪处理后的波形图。同时,对比这4种方法与本文中优化方法的客观降噪指标。考虑到实测信号先验知识未知,不能采用信噪比和均方误差来定量比较不同方法的降噪效果。信号都有一定的相关性,而噪声不相关,因此,信号的自相关函数远大于噪声[11]。如表4所示,新的优化方法降噪后的信号自相关系数大于其他方法,从而进一步体现了新的优化方法降噪的优越性。

表4 实测信号降噪效果对比Tab.4 Comparison of noise reduction outcomes of measured signal
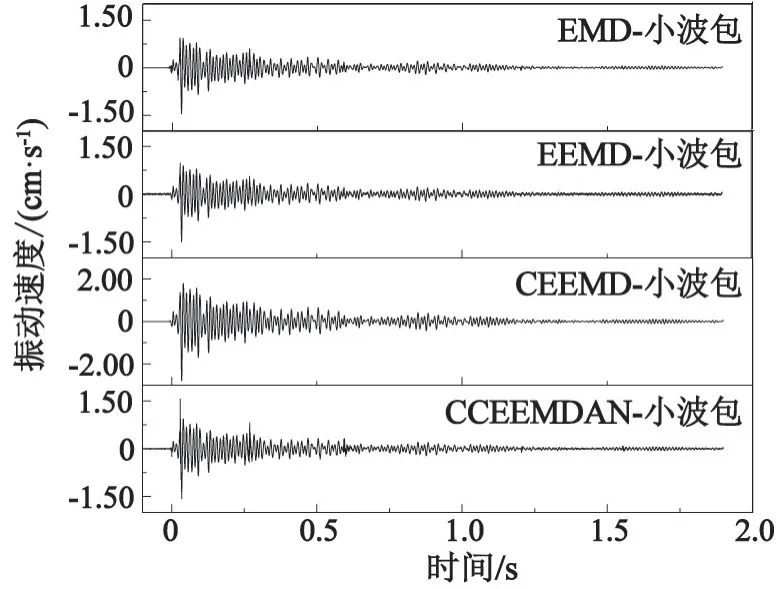
图6 降噪效果对比Fig.6 Comparison of noise reduction outcomes
4 结论
针对CEEMDAN-小波包联合降噪方法存在的不足,以新建太锡铁路太崇段隧道3#斜井正洞爆破施工为例,通过仿真测试和对实测爆破振动信号处理,提出了CEEMDAN-小波包联合降噪的优化方法,并得到以下结论:
1)CEEMDAN-小波包联合降噪方法利用多尺度排列熵和SG平滑滤波算法进行优化,进一步提高了爆破振动信号的降噪效果,且有效保留了原始信号中的特征信息。
2)与4种常见的与小波包联合算法进行对比,新的优化方法降噪后的各项指标均优于其他算法,且有较好的自相关性,降噪效果最好,为爆破信号精确分析提供了一种有效的优化方案。
