一种权衡性能与隐私保护的推荐算法

马黛露丝,朱海萍,田锋,冯沛,陈妍,计湘婷,李玉杰

(1.西安交通大学电子与信息学部,710049,西安;2.西安交通大学陕西省天地网技术重点实验室,710049,西安;3.百度时代网络技术(北京)有限公司,100085,北京;4.南京理工大学计算机科学与工程学院,210094,南京)

推荐算法在电商系统、学习平台等的应用为用户高效、便捷的使用提供了有力保障。但是,由于推荐的结果建立在用户各类数据之上,推荐系统也存在隐私泄露的风险。以在线学习为例,根据推荐系统提供的推荐列表,攻击者可以推测出不同学习者的偏好,再结合学习日志等辅助信息,甚至可以反向推测出特定偏好对应的学习者,从而获取其姓名、学校、专业、学号、客户端IP地址等真实身份信息[1]。虽然用户的姓名、电话等信息往往不作为推荐系统使用的特征,不影响推荐精度,但是若攻击者反推得到用户偏好,进而反推得到对应该偏好的用户,便会造成用户真实身份信息及偏好数据的隐私泄露,相比于电商系统中的虚拟账户信息,此类包含真实身份的信息需要的隐私保护程度更高,因此在线学习平台的隐私保护越来越受到公众的关注。在线学习平台大多缺少显式评分,存在数据不平衡问题,并且大多使用基于隐式反馈的推荐系统,此类系统相比于显式系统,在数据处理、用户偏好建模等阶段更为复杂,实施代价更大[2-4],因此如何在隐私保护程度与推荐精度之间均衡十分重要。

针对推荐系统的隐私保护安全问题,国内外学者的研究主要分为数据加密技术、基于数据模糊技术和差分隐私保护技术[5-6]。差分隐私保护技术在保证算法对特定统计结果的输出概率不发生显著变化的前提下,利用算法对数据集的统计结果随机化处理,保护原始数据信息,其差分隐私保护参数能够描述使用的随机算法给出的最高隐私保护水平[7]。差分隐私已被应用到矩阵分解推荐模型中,评估隐私保护和推荐效率的权衡效果[8]。之后的研究将差分隐私技术与贝叶斯后验采样融合,能够得到推荐准确率更高的差分隐私推荐框架[9]。Meng等通过在敏感和非敏感数据的训练集中引入不同的噪声强度,保护了社交推荐系统的隐私[10]。现有的针对在线学习平台的基于邻域的差分隐私保护推荐算法[11],在计算用户或项目相似度矩阵时,会因稠密的矩阵临时存储表而占用相当的内存,而矩阵分解的推荐算法在训练过程中不需要存储与维护相关表,节省内存,如在包括4多万用户的Netflix Prize数据集中,使用基于邻域的推荐方法,大约需要30 GB内存,而矩阵分解推荐方法只需要4 GB内存。

本文针对在线学习资源推荐平台隐式反馈的性质,提出基于资源热度负采样算法,解决隐式反馈系统中数据不平衡的问题,使用差分隐私保护参数ε描述隐私保护程度分级,提出性能与隐私保护均衡的推荐算法,研究矩阵分解的差分隐私保护算法中隐私保护参数与推荐精度的关系。

1 基于矩阵分解推荐模型的隐私泄露风险分析

在推理攻击与重构攻击[12]两种攻击模型的攻击下,矩阵分解模型存在隐私泄露的风险。其中,推理攻击通常被用于推断某个模型的训练集中是否包含某个体的评级;重构攻击是根据目标受害者的一些背景信息,预测其敏感特征的准确值。当两种攻击结合起来[13],在基于矩阵分解的推荐过程中,攻击者首先借助推理攻击推断数据集中是否包括目标攻击用户的评级,其次通过重构攻击,利用已知的部分评级反向预测受害用户的潜在特征,便能发现用户的偏好信息以及其他潜在敏感信息[14]。

矩阵分解推荐模型中攻击者的反向预测过程如文献[15]所述,受害者用户u1与攻击者共享更新后的项目因子V,若攻击者掌握的背景信息为受害者非敏感的偏好评级R12,则可以通过u1=v2R12-1反推出受害者向量u1,从而进一步根据R1i=u1V获取受害者的其余敏感的偏好评级,造成用户向量、偏好向量等隐私泄露。

2 性能与隐私保护均衡的推荐算法

根据上述对推荐中矩阵分解模型隐私泄露风险的分析,本文在所提出的性能与隐私保护均衡的推荐算法中,使用基于矩阵分解的差分隐私保护推荐算法[6]作为基础推荐模型,分析其中隐私保护参数与推荐精度的关系,以在线学习资源推荐平台为例,研究框图如图1所示。因矩阵分解的目标优化函数为非凸函数,对求解结果的敏感度较高,在输出模块引入噪声会使预测结果的可用性大大降低,因此本文只分析矩阵分解模型中分别在数据输入和模型训练模块引入差分隐私保护方法的结果。在数据准备部分,本文针对在线学习用户数据的隐式反馈特点,提出基于资源热度负采样算法,对推荐模型的输入数据进行样本平衡处理。

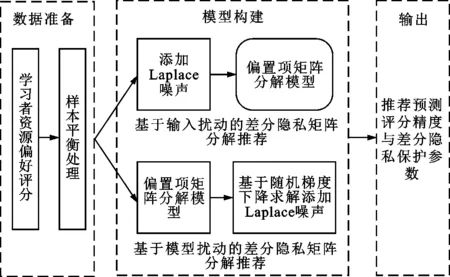
图1 性能与隐私保护均衡的推荐算法研究框架

2.1 基于输入扰动的差分隐私矩阵分解推荐算法

基于输入扰动的差分隐私矩阵分解推荐算法是基于差分隐私保护的原理,在推荐模型训练之前对构建的隐式反馈评分引入噪声,之后再构建矩阵分解模型。对于样本平衡处理后得到的用户项目偏好评分矩阵R使用下式引入噪声,即

(1)

式中:Δf表示敏感度。根据差分隐私保护的性质,最终得到的偏好评分矩阵Λ(R)满足ε差分隐私保护。

2.2 基于模型扰动的差分隐私矩阵分解推荐算法

基于模型扰动的差分隐私矩阵分解保护推荐算法在梯度下降的每一步迭代中,对误差函数进行Laplace噪声的添加,此过程也称梯度加扰[16]。同时,每一次迭代算法都满足ε/e差分隐私,根据差分隐私保护的组合性质,则在e次迭代计算后,最终整个偏置项矩阵分解满足ε=eε/e差分隐私保护。

2.3 基于资源热度负采样算法

隐式反馈推荐系统中只有用户的操作历史行为,缺少用户的负反馈样本,导致的样本不平衡问题会影响到推荐精度,为此参考已有的引入负样本的4种策略[13],结合汤普森采样算法[17]在推荐系统中的应用,针对在线学习资源推荐系统,提出基于资源热度负采样算法,其中资源热度与资源item出现的次数成正比,热门资源是指资源热度大于所设阈值的资源。使用基于资源热度负采样算法使得负采样后的平衡数据满足以下3点特征:

(1)对于每个学习者,负采样后保证正负样本的数目均衡;

(2)对于每个学习者,进行负样本的选择时,负样本取自同一课程下的资源库中;

(3)在进行负采样的时候,在学习者没有操作的热门资源中,利用β分布随机选取资源。

基于资源热度负采样算法的具体步骤如算法1所述,在同类课程下,item_list_all是所有视频资源的列表,item_list则是代表学习者已经有过操作行为的资源视频的集合。

算法1基于资源热度负采样算法:

输入学习者编号user_id,学习者有操作行为的某课程视频资源列表item_list,某课程所有视频资源列表item_list_all

输出正负样本均衡的样本数据sample

1: sample={}

2: for item in item_list do

3: sample[item]=user_item_rating

4: end for

5: candidate_list=Thompson(item_list_all)

∥在热门资源中使用汤普森采样获得资源列表

6: for item in candidate_list do ∥负采样

7: if item in sample then

8: continue

9: end if

针对旅游英语专业学生跨文化交际能力这一测试主体，笔者对我校旅游英语专业的80名学生进行了调查，并根据调查结果进行了定量分析。

10: sample[item]=0 ∥负样本评分置零

11:n+=1

12: ifn=len(item_list) then

13: break ∥保证正负样本数均衡

14: end if

15: end for

16: return sample

3 实验与结果分析

3.1 实验设计

3.1.1 实验数据集 本文主要依托西安交通大学网络学院学习平台(以下简称网络学院),选取网络学院计算机专业第4学期的《操作系统原理》《计算机网络原理》《数据结构》《计算机组成原理》《编译原理》和《Java语言》6门课程,分析在线学习者与视频学习资源的交互行为,将其总结为学习者的视频学习次数偏好、视频学习时长偏好、视频学习暂停拖动次数偏好3种操作行为,以三者的算数加权作为学习者对课程视频的评分,具体表示如下

(2)

式中:α=1;β=5;γ=4[11];pf(ui,vk)∈[0,1]为视频学习次数偏好,由学习者ui观看视频vk的累计次数f(ui,vk)计算得到;pd(ui,vk)∈[0,1]为视频学习时长偏好;d(ui,vk)为累计时长;dvk为原始时长;ppd(ui,vk)∈[0,1]为视频学习暂停拖动次数偏好[18];p(ui,vk)为ui暂停vk的累计次数;g(ui,vk)为ui拖动vk的累计次数。对于给定的学习者与给定课程,可以得到基于学习行为偏好的评分,从而得到基于学习者学习行为偏好的学习者课程视频评分矩阵,以下统称为学习者学习资源评分矩阵,并以此作为后续实验的基础。

3.1.2 实验结果评价指标 依据所选取的网络学院的99 732条视频资源日志作为原始数据,计算得到学习者对资源的偏好评分矩阵,使用五折交叉验证方法选取测试集与训练集,实验应用百度飞桨深度学习框架平台完成。

本文实验首先选取不同的隐私保护参数,计算最终算法得到的推荐精度,探讨隐私保护参数与推荐精度的关系;其次,比较是否使用基于资源热度负采样算法进行数据处理的推荐精度,分析样本平衡性对模型的影响。实验采用的算法性能评测指标为均方根误差r,这类指标常被用于评估推荐算法的预测评分精度(以下简称推荐精度)。r越小,预测的评分越准确,计算式如下

(3)

3.2 输入扰动差分隐私推荐算法实验与结果分析

3.2.1 实验设计 为验证在输入扰动模型下所提资源热度负采样算法的有效性,以及探讨隐私保护参数与推荐精度的关系,采用的对比实验有不添加噪声的基于随机梯度下降法求解的基本矩阵分解推荐算法(Clean MF)、不添加噪声的偏置项矩阵分解推荐算法(Clean Biased MF),以及添加噪声的基本矩阵分解推荐算法(INR MF)。其中,Clean MF用来对比偏置优化后的矩阵分解推荐算法与Clean Biased MF的推荐精度,INR MF用来与INR Biased MF对比在不同隐私保护参数下的推荐精度损失程度。

3.2.2 实验结果分析 选取不同的隐私保护参数,根据Laplace噪声的生成方法可视化其噪声分布发现,当ε的取值越小,所添加的噪声分布越分散且噪声值大,此时算法的隐私保护程度比较高;反之,当ε取值越大,所添加的噪声趋于0,此时算法所损失的效用性最小,但相应的隐私保护程度也降低。

(1)算法推荐精度与隐私保护参数的关系分析。分析在不同的隐私保护参数下推荐算法的推荐精度,其中参数设置如下:隐式分解维度为3,正则化参数为0.1,迭代次数为30,梯度下降学习速率为0.02。

实验结果如图2所示,其中红色曲线明显低于绿色曲线,表示在无噪声添加的情况下,考虑用户以及项目的偏置因素会使得推荐精度更高。在进行噪声的添加后,如蓝色与橘色曲线所示,在基于输入扰动的情况下,偏置项矩阵分解对噪声的敏感度更低。橘色曲线表示随着ε的增加,带偏置项矩阵分解的推荐r逐渐降低,并在ε=15时趋近于无噪声的推荐精度,这与我们的理论分析也相符合,即r∝1/ε,因此针对不同的推荐系统隐私保护程度需求以及推荐精度要求,可以选取对应的ε。

图2 平衡样本中输入扰动时不同算法的推荐精度比较

(2)样本的平衡性对于算法推荐精度的影响。在未经过样本平衡处理的原始评分矩阵上进行相同的推荐实验,结果如图3所示,与图2所得均方根误差曲线趋势相同。

图3 非平衡样本中输入扰动时不同算法的推荐精度比较

输入扰动下平衡样本与非平衡样本上的实验结果如图4所示。由图可知,无论是否添加噪声扰动,平衡样本下的推荐r都低于非平衡样本下的,并且ε取值越大影响越明显,说明在隐式反馈的矩阵分解推荐中进行样本平衡处理是必要的。

图4 输入扰动下样本平衡性对推荐精度的影响

3.3 模型扰动差分隐私推荐算法实验与结果分析

3.3.1 实验设计 为验证在模型扰动算法下的结果,采用的对比实验有Clean MF、clean Biased MF、添加噪声的基本矩阵分解算法(MNR MF)、带偏置项矩阵分解算法(MNR Biased MF)以及文献[20]中的差分隐私保护全局平均值(Global average)和差分隐私保护项目平均值(Item average)两种方法。

3.3.2 实验结果分析

(1)算法推荐精度与隐私保护参数的关系分析。不同ε下推荐算法精度的比较如图5所示。实验中相关参数的设置如下:隐式分解维度为3,正则化参数为0.05,梯度下降学习速率为0.01。由图5可知,当ε≥5时,本文所使用的MNR Biased MF推荐精度高于Global average和Item average的推荐精度。观察图5中MNR MF与MNR Biased MF的推荐精度与隐私保护参数的关系发现:ε=1时,推荐精度相近;ε<1时,即隐私保护程度比较高的时候,MNR MF算法推荐精度更高;ε>1时,MNR Biased MF算法推荐精度更高。这表示MNR Biased MF的矩阵分解对过高的噪声引入敏感性较高,但在隐私保护程度适中(ε≥5)的情况下,推荐精度在不损失过多时远高于MNR MF。

图5 平衡样本中模型扰动时不同算法的推荐精度比较

(2)样本的平衡性对于算法推荐精度的影响。在未经过样本平衡处理的原始评分矩阵上进行相同的推荐实验,结果如图6所示,与图5所得均方根误差曲线趋势相同。

图6 非平衡样本下模型扰动时不同算法的推荐精度比较

样本平衡与非平衡下的实验结果如图7所示。无论是MNR MF还是 MNR Biased MF,样本平衡后的推荐精度都更高。对于MNR Biased MF,当ε≤4时样本平衡处理的效果更加明显,而对于MNR MF,ε≤2时样本平衡处理的效果更加明显。这表明样本平衡性对于MNR MF的影响更显著,因此实际中采用本节提出的MNR Biased MF能更好地均衡推荐精度与隐私保护程度。

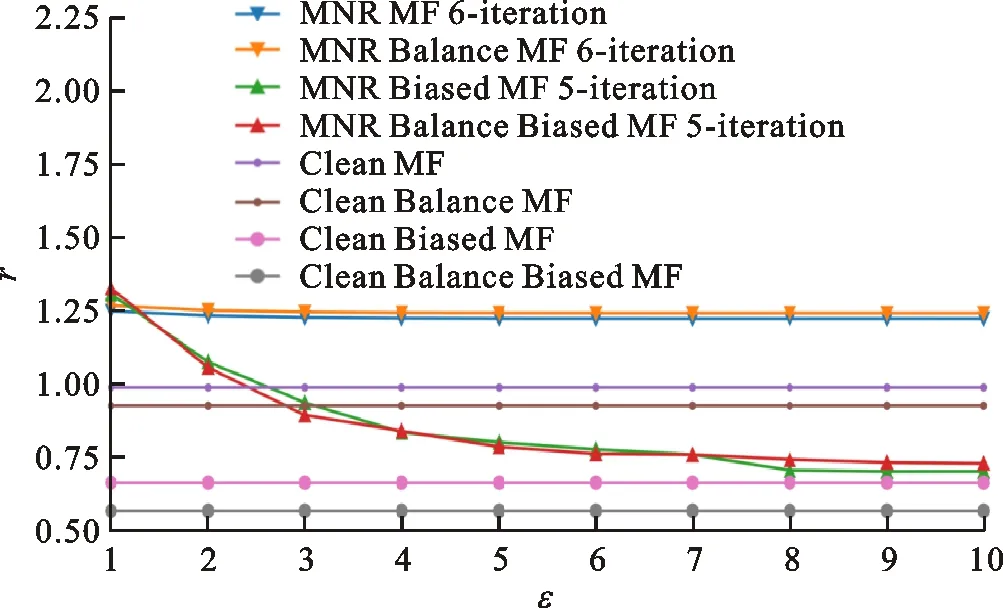
图7 模型扰动下样本平衡性对推荐精度的影响

3.4 均衡优化与对比分析

根据上述实验中发现的ε越小隐私保护程度越高,r越小推荐精度越好,以及r与1/ε正相关的关系,可对min-max标准化后的两个变量构造优化目标如下

min(w1r+w2ε),w1+w2=1

(4)

经实验发现,当w1<0.6时,r精度差,ε倾向取最小值;当w1=0.6,输入扰动下在ε=7时,模型扰动下在ε=3时,平衡样本与样本非平衡实验场景下的推荐精度与隐私保护程度达到均衡最优。

同时对比分析发现:在不同的ε下,如表1所示,相同隐私保护程度下无论样本平衡与否,在ε取值较小时,基于模型扰动的推荐精度优于基于输入扰动的,但当ε取较大值(ε>5)时,基于输入扰动的推荐精度优于基于模型扰动的。

表1 模型扰动算法与输入扰动算法推荐预测评分精度比较

4 结论及展望

根据本文实验结果可知,矩阵分解的差分隐私保护推荐方案中,无论是输入扰动还是模型扰动,样本平衡处理后推荐精度会提高,其对应的推荐精度与差分隐私保护参数的倒数均呈正比关系,特别地,输入扰动与模型扰动分别在ε取值7和3时,推荐精度与隐私保护程度达到均衡。当隐私保护程度较高,即ε≤5时,基于模型扰动的差分隐私矩阵分解推荐在相同的隐私保护程度下,优于基于输入扰动的;当隐私保护程度较低,即ε>5时,基于输入扰动的差分隐私矩阵分解推荐在相同的隐私保护程度下,优于基于模型扰动的。根据模型扰动算法对系统模型维护有更高要求的特点可得,对于隐私保护程度要求很高的推荐系统,建议采用基于模型扰动的矩阵分解差分隐私推荐,对于隐私保护程度要求适中的推荐系统,建议采用维护成本较低的基于输入扰动的矩阵分解差分隐私推荐算法。

目前,差分隐私保护与在线学习资源推荐相结合的研究还相对较少,本文所提出的方案是一次很有意义的尝试,有较强的实际应用价值,但仍有优化和完善的空间,下一步的工作将研究在增量隐式反馈数据下推荐算法的隐私保护问题。