采用强化学习的多轴运动系统时间最优轨迹优化
2021-07-13张铁廖才磊邹焱飚康中强
张铁,廖才磊,邹焱飚,康中强
(华南理工大学机械与汽车工程学院,510641,广州)
在多轴运动系统的自动化装配、搬运等生产过程中,往往要求系统能够高速运动以提高生产效率,但是系统的高速运动可能会导致电机动载荷过载的问题,这一现象在重载运动时尤为明显,不仅对电机产生损害,还降低了生产质量。
为实现多轴运动系统的高速运动,需要以时间最优为目标对轨迹进行优化[1-3]。为了进一步解决高速运动过程中的电机动载荷过载问题,需要将电机动态载荷视为约束条件引入到时间最优轨迹优化数学模型中,如文献[4]通过对系统建立动力学模型,并在轨迹优化时增加电机动态载荷约束,从而得到理论计算力矩,满足电机动载荷约束的时间最优轨迹。但是,由于电机动子电流和定子磁场畸变以及机械参数变化等扰动,所建立的动力学模型和实际模型无法完全匹配,最终实际测量力矩仍会超出电机动载荷限制。因此,文献[5]在动力学模型中增加补偿项并利用迭代学习方法来更新补偿项,以此提高动力学模型精度。虽然能够在一定程度上减小模型不匹配度,但其仍是对理论计算力矩进行约束,无法从根本上解决高速运动中电机动载荷过载的问题。
近年来,强化学习[6]在控制领域已经有了广泛的研究应用,例如移动路径规划[7-8]、步态生成[9-10]、避障[11-12]和装配[13-14]等。这些研究用马尔可夫决策过程来描述实际物理问题,然后利用强化学习方法进行学习求解。本文也基于马尔可夫决策过程对时间最优轨迹优化问题进行研究,利用强化学习中智能体与环境进行交互学习的特性,提出了一种采用强化学习的时间最优轨迹优化方法:首先,将时间最优轨迹优化问题描述为马尔可夫决策问题;其次,对经典的状态-动作-奖励-状态-动作(SARSA)算法[15]进行改进,使其能适用于时间最优轨迹优化;最后,通过迭代交互法与真实环境交互学习,从而获得满足运动学约束和动力学约束的时间最优轨迹。本文方法无需建立动力学模型,而是直接对电机实际力矩进行约束,避免了动力学模型和实际模型不匹配的问题,从根本上解决了多轴运动系统在高速运动中电机动载荷过载的问题。
1 时间最优轨迹优化的强化学习环境
时间最优轨迹优化问题实质上是寻找满足约束条件的电机运动轨迹,使其以尽可能大的速度工作,从而达到时间最优。为了采用强化学习方法解决时间最优轨迹优化问题,首先需要基于运动学约束条件来构造强化学习环境,动力学约束的引入需要通过与真实环境的迭代交互来完成,具体将在2.2小节研究。
1.1 时间最优轨迹优化的运动学约束
多轴运动系统包括串联结构和并联结构,本文主要研究串联结构,如数控机床、串联工业机器人等。图1是多轴运动系统示意,可以看出,轴的运动方式主要分为转动和移动两种,前3轴为转动轴,第4轴为移动轴。结构的选用及组合需要根据应用场景来设计,本文暂不考虑具体结构,只针对电机进行描述,记电机转角关于时间t的函数为q(t)=[q1(t)q2(t)…]T。

图1 多轴运动系统示意
为了减少优化过程中的变量,轨迹优化往往在相平面上进行[16]。假设路径标量s∈[0,1][17]与时间t存在函数映射关系s(t),则有
q(t)=q(s)
(1)
进一步地,可得到电机角速度和角加速度关于标量s的表达式

(2)
(3)

(4)
(5)
(6)
(7)


(8)
1.2 基于运动学约束的强化学习环境
对任一条运行时间为tf的完整电机轨迹,不失一般性地,假设
s(0)=0≤s(t)≤1=s(tf)
(9)
(10)
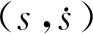
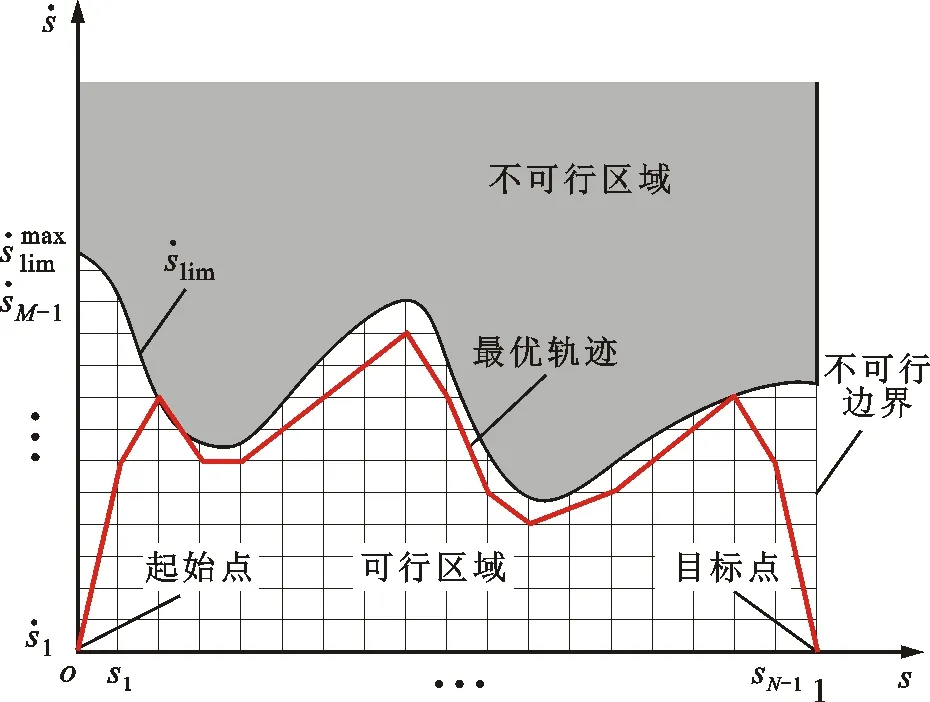
图2 时间最优强化学习环境示意
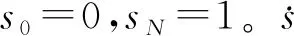
2 时间最优轨迹优化的强化学习算法
2.1 改进SARSA算法
SARSA算法[19]是一种经典的强化学习算法,其中,状态是智能体在环境中的位置,动作是智能体从一个状态转移到另一个状态所采取的行动,奖励是环境对智能体的一个反馈。记Q(Sk,Ak)为智能体在状态Sk采取动作Ak时获得的平均奖励,则用于时间最优轨迹优化的SARSA算法的学习过程如图3所示。智能体从状态S0开始,在状态Sk根据Q(Sk,Ak)采取一个动作Ak,之后从环境中获得奖励Rk+1,更新Q(Sk,Ak)并到达下一个状态Sk+1,这一连串状态动作的组合称为一个情节。
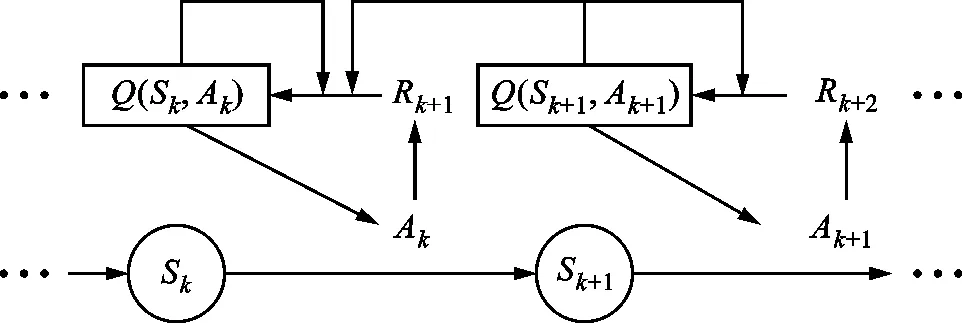
图3 SARSA学习过程
2.1.1 动作 SARSA算法中,动作的选择采用ε贪心法,公式为
(11)
式中λ为随机数。
ε贪心法基于概率ε(0≤ε<1)对探索和利用进行折中:每次学习时,以ε的概率进行探索,即以均匀概率随机选择一个动作,以发现可以获得更大奖励的动作;以1-ε的概率进行利用,即选择当前状态下最大的Q所对应的动作,以尽可能多地获得奖励。此外,当处于倒数第二个状态时,如果通过计算发现终止目标状态点(1,0)刚好在可选择的动作范围内,那么这个终止目标状态为唯一可选的动作。

(12)
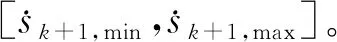
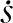
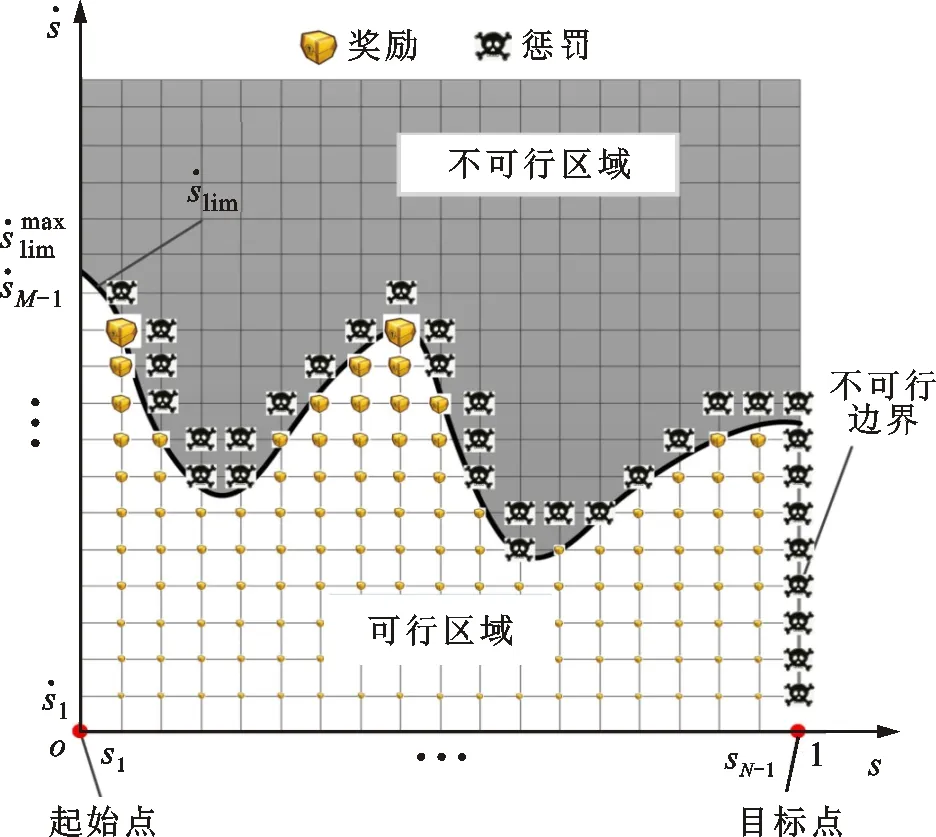
图4 时间最优轨迹优化问题的奖励和惩罚示意
(13)
2.1.3Q表 在经典的SARSA算法中,状态动作函数为
Q(Sk,Ak)←Q(Sk,Ak)+α(Rk+1+
γQ(Sk+1,Ak+1)-Q(Sk,Ak))
(14)
式中:α为学习系数,0≤α<1,α越大则表示靠后的积累奖励越重要;γ表示折扣因子,0≤γ<1。
由于SARSA算法是一个单步更新的强化学习算法,当智能体到达一个不可行状态点并受到惩罚时,它只能通过单步更新,将惩罚往前回溯到前一步。因此,需要相当多的时间去更新Q才能使不可行状态点的Q小于0,以保证智能体不再经过这些状态点。为了加速这个惩罚的传导过程,应该在智能体经历过一段失败的情节时,便对该段情节上的所有动作进行惩罚,使该段情节上的所有动作都能从这次失败的情节中学到经验。改进的状态动作函数通过在状态动作后面增加一个惩罚项用来加速惩罚,公式为
Q(Sk,Ak)←Q(Sk,Ak)+α(Rk+1+
γQ(Sk+1,Ak+1)-Q(Sk,Ak))+ρK-kRK+1
(15)
式中:K表示这段失败的情节一共经历的状态数,0≤k≤K;RK+1表示智能体在到达第一个不可行状态点时受到的惩罚;ρ表示惩罚折扣因子,0<ρ<1,ρ使越靠近不可行区域的动作受到的惩罚越大。
至此,得到改进SARSA算法的学习框架,如图5所示。初始化Q表,利用改进SARSA算法进行情节学习,在经历过一段成功的情节之后,将贪婪策略的贪婪因子ε设置为0,用于对学习到的经验进行开采以获得最优策略,并保存这段最优策略轨迹;重新设置一个在0~1之间的贪婪因子用于探索,并在获得另一个成功的情节之后,重新将贪婪因子ε设置为0进行开采,获得新的最优策略轨迹;如果新获得的最优策略轨迹和保存的最优策略轨迹一样,则表明智能体可能已经遍历了所有可能的情况,并且算法收敛于最优策略。

图5 改进SARSA算法的框架
2.2 迭代交互法
根据3.1小节中的改进SARSA算法,可以学习到一条满足运动学约束的初始策略轨迹,但是由于算法并未考虑动力学约束,因此当执行这条轨迹时,电机实际测量力矩可能超限。所以,需要通过与真实环境进行迭代交互来引入动力学约束,并对初始策略轨迹进行修正,使电机实际测量力矩最终能够满足动载荷约束。时间最优轨迹优化问题的迭代交互法框架如图6所示,主要包括以下3步。

图6 迭代交互法框架
第1步 将时间最优轨迹优化的运动学约束条件构建成强化学习环境,将时间最优轨迹优化问题构建成强化学习模型。
第2步 使用改进SARSA算法学习得到策略轨迹。
第3步 在真实环境中运行获得策略轨迹,并采集真实的测量力矩,判断是否超限,如果超限则将那些超限部分的状态点都设置为不可行状态点,从而将动力学约束更新到强化学习环境中。
重复第2、3步,直到测量力矩不再超限,便可获得一条同时满足运动学和动力学约束的时间最优轨迹。
3 仿真与实验
3.1 改进SARSA算法仿真
为了验证改进SARSA算法的有效性,在MATLAB R2018b对改进SARSA算法进行仿真验证。考虑到实际工况中路径的曲率多变性,本文用NURBS曲线插补器[20]生成一条曲率多变的星形曲线轨迹,并对其进行优化。星形曲线的参数中,次数k=2,节点矢量U=[0,0,0,1/9,2/9,3/9,4/9,5/9,6/9,7/9,8/9,1,1,1],顶点参数如表1所示。插补生成的轨迹如图7所示。
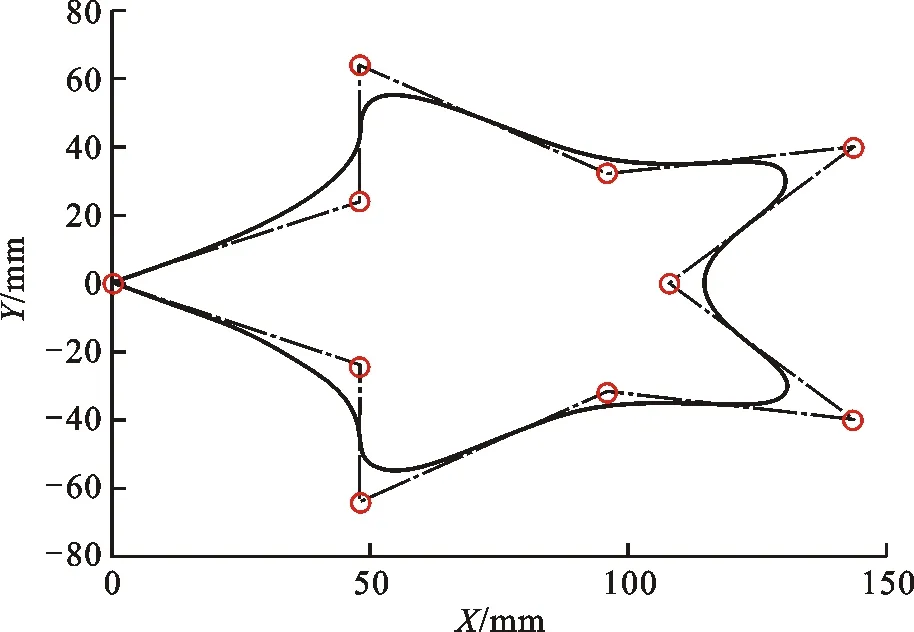
图7 星形曲线轨迹

表1 星形曲线顶点参数
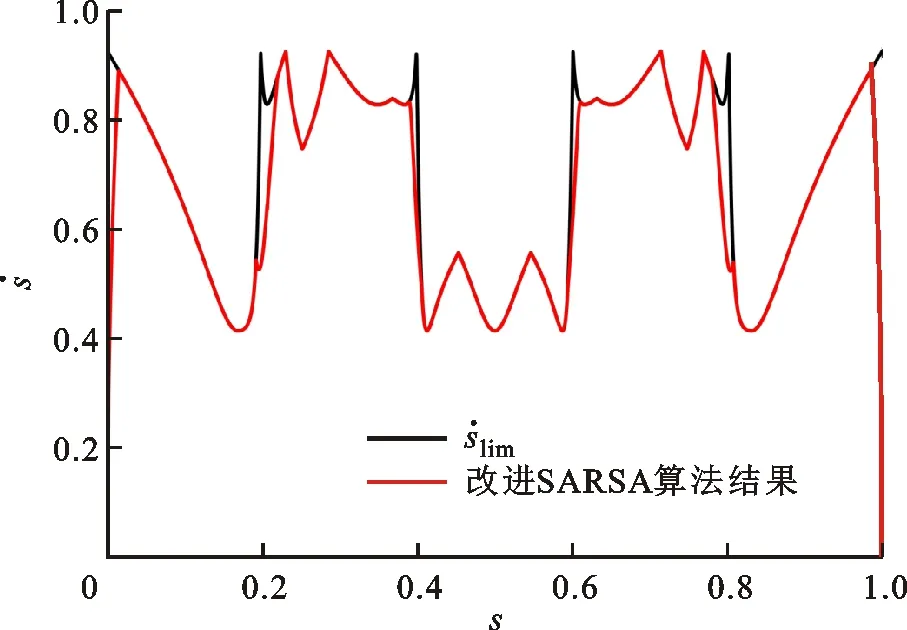
图8 相平面轨迹优化结果
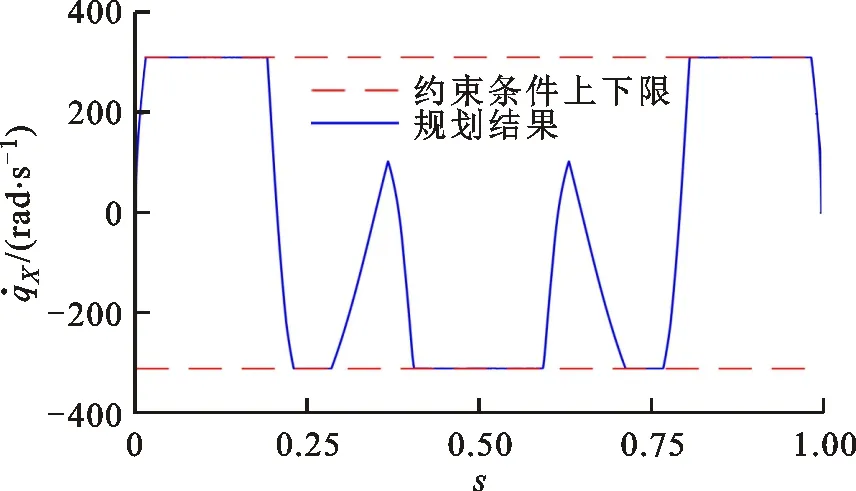
(a)X轴速度曲线
3.2 迭代交互实验
时间最优轨迹优化的迭代交互实验平台如图10所示,平台由做独立运动的X、Z两轴串联组成。两轴的电机的型号均为Delta ECMA-CA0604RS,由Delta ASD-A2-0421-E交流伺服驱动器进行驱动,再经过滚珠丝杠将旋转运动转换成工作台的直线运动。平台的控制系统搭建于Windows7 64-bit系统,并使用EtherCAT工业以太网进行通信,控制周期和采样周期均为1 ms。作为主站的工控机型号为DT-610P-ZQ170MA,CPU为Intel Core i7-4770,最高主频为3.40 GHz,运行内存为8 GB。

图10 实验平台
利用3.1小节中改进SARSA算法优化得到的策略轨迹与真实环境进行迭代交互实验,结果如图11所示。可以看出,动载荷过载点的数量随着迭代的进行逐渐减少,且经过10次迭代之后,动载荷过载点的数量减少为0。

图11 电机动载荷过载点数
迭代前和经过10次迭代后的实际测量力矩曲线如图12所示。可以看出,迭代前X轴的部分实际测量力矩曲线超过了动载荷限制,而经过10次迭代后,X轴和Z轴的实际力矩曲线均在动载荷限制内。这是因为改进SARSA算法并未考虑动力学约束,在运行迭代前的策略轨迹时,部分点的电机动载荷过载。与真实环境进行迭代交互后,动力学约束被引入,策略轨迹逐渐得到修正,最终轨迹的实际测量力矩满足动载荷限制。由此,迭代交互法的有效性得到了验证。

(a)X轴力矩曲线
4 结 论
为实现多轴运动系统高速运动并解决电机动载荷过载的问题,本文将时间最优轨迹优化问题描述为马尔可夫决策问题,提出了一种采用强化学习的时间最优轨迹优化方法。该方法无需建立动力学模型,而是通过与现实环境的交互学习来直接对实际力矩进行约束,避免了动力学模型和实际模型不匹配的问题,从根本上解决了多轴运动系统在高速运动中动载荷过载的问题。
采用强化学习的时间最优轨迹优化方法根据时间最优轨迹优化问题的特性对经典SARSA算法进行改进,通过与基于运动学模型建立的强化学习环境进行交互学习,找到满足运动学约束的初始策略轨迹。通过迭代交互法与真实环境进行交互学习,从而将动力学约束引入到强化学习环境中并对策略轨迹进行修正。最终,获得同时满足运动学约束和动力学约束的时间最优轨迹。
实验结果显示,改进SARSA算法优化得到的策略轨迹的速度和加速度曲线均在约束内,且经过10次迭代后的轨迹实际测量力矩曲线也均在动载荷约束内,提出的采用强化学习的时间最优轨迹优化方法有效。
