电子轰击式离子推力器放电腔结构对等离子体特性影响的全粒子仿真研究

2021-07-13孙安邦闫涵李昊霖

西安交通大学学报 2021年7期

孙安邦,闫涵,李昊霖

(西安交通大学电气工程学院,710049,西安)

电推力器主要应用于深空探测器、通信卫星及空间科学实验等方面[1],其中离子推力器因比冲高、寿命长、控制精度高等优点受到重视,被广泛应用于航天工程中。放电腔是电子轰击式离子推力器产生并引出等离子体的关键部件,其结构是决定离子生成效率、均匀性、单一性的关键,并对推力器的推力、比冲、效率和寿命有着重要影响[2]。放电腔内产生等离子体的过程是:空心阴极发射高能初始电子与推进剂中性粒子发生碰撞电离,生成等离子体,等离子体中的离子通过电场加速向放电腔出口运动并被引出到栅极,其结构如图1所示。在放电腔设计中需要考虑到工质气体进气口位置以及空心阴极位置这些结构参数。调整进气口位置可以改变工质气体在腔内的运动路程,进而改变主要发生碰撞电离的区域,影响电离率;空心阴极的长度会影响腔内电子分布以及离子的回流程度,改变引出离子的分布以及效率。离子光学系统的运行对等离子体密度有着一定的要求,离子均匀性会显著影响栅极寿命[3]。因此,需要进一步开展相关研究来分析不同因素对放电腔等离子体特性的影响。

图1 电子轰击式离子推力器放电腔结构示意图

由于放电腔体的封闭结构给实验测量带来了一定的局限性和困难,为了研究放电腔内的电离过程和引出机理,近年来科研人员开展了大量的数值模拟工作。Brophy等基于能量守恒方程建立了离子推力器放电腔数值模型,确定了产生等离子体所需的能量,研究了改善推力器性能的方法[4]。Goebel等建立了自洽等离子体放电模型,计算了放电腔内的等离子体密度、能量和电势,发现磁场对壁面附近的等离子体密度影响较大[5]。Wirz等建立了二维轴对称混合模型,对二次电子和离子采用流体描述,模拟得到了腔内磁场、密度分布和电流密度等参数[6]。Mahalingam等开发了二维粒子模拟结合蒙特卡罗的全粒子模型[7]。该模型考虑了放电腔内的初始电子、二次电子、单价和双价离子以及中性粒子5种主要粒子,并采用人为增大介电常数的方法加速计算[8],主要研究了粒子权重、时间步长和磁场大小等因素对等离子体分布的影响。Stueber建立了放电腔三维粒子模型,主要研究了磁场对初始电子的影响[9]。兰州空间技术物理研究所陈娟娟等采用网格粒子和蒙特卡罗碰撞(PIC/MCC)方法对LIPS-200离子推力器放电腔原初电子动力学行为进行了模拟,研究了电磁场对原初电子的影响以及等离子体的运动特性[10]。

目前,对于离子推力器放电腔的研究,主要采用的是混合模拟和全粒子模拟。混合模拟相比全粒子模拟计算量较小,但是由于对部分粒子做了流体近似,因此不能得到局部粒子的微观特性。对于大多数采用全粒子模拟的研究,主要是对放电腔内工作特性进行描述,或只针对仿真中的计算参数如粒子权重、时间和空间步长对等离子体特性的影响,以及磁极结构对推力器某一特性的影响[5-10],而进气口位置和空心阴极长度对离子推力器放电腔的优化设计有着重要的参考意义,且相关研究不充分,有必要进行深入讨论。因此,本文基于PIC/MCC方法,采用全粒子的二维轴对称模型,仿真研究了不同工质气体进气口位置以及阴极位置对放电腔等离子体特性的影响,并对仿真结果进行分析。

1 仿真模型及参数设置

1.1 放电腔模型

鉴于放电腔的轴对称性,可以在二维柱坐标下对其进行模拟,本文的仿真区域长10 cm,半径5 cm,栅极半径为4.5 cm,放电腔外包围着3个环状钐钴永磁体,如图2所示。

图2 放电腔计算结构示意图

本文仿真采用静电模型,通过泊松方程求解电势

(1)

式中:φ为电势;ε0为真空介电常数;e为元电荷;ni和ne分别表示离子和电子密度。在二维轴对称柱坐标下,式(1)可展开为

(2)

式中z和r分别表示轴向和径向坐标。

本文采用超松弛迭代法来求解式(2),放电腔内电场通过电势梯度得到,即

E=-φ

(3)

带电粒子的运动遵循牛顿运动定律[11]

(4)

式中m、q、v分别为带电粒子的质量、电荷以及速度。本文采用Boris算法[12]求v和x。Boris算法首先通过半个时间步长的电场加速,速度由vn-1/2更新为v-;接着在一个时间步长内,粒子的旋转速度由v-更新为v+;最后再经过半个时间步长的电场加速,速度更新为vn+1/2。具体计算公式如下

(5)

式中:上标n表示当前时刻;t′和s′分别定义为

(6)

(7)

根据求解的速度,粒子位置可更新为

xn+1=xn+vn+1/2Δt

(8)

仿真中主要考虑了电子与中性粒子之间的弹性、激发和电离碰撞,以及离子与中性粒子之间的弹性碰撞和电荷交换碰撞。工质气体选择氙气,并在仿真的最开始通过直接蒙特卡罗碰撞(DSMC)的方法进行模拟,得到其空间密度和速度分布特征,并在之后带电粒子的计算中设置为背景气体。

为了简化计算,本模型采用空碰撞的方法[11]使总碰撞率恒定。最大碰撞频率为

Ri=max(nneu)max(σiv)

(9)

式中:nneu为背景粒子数密度;σi为目标粒子与背景粒子的碰撞截面;v为目标粒子速度。带电粒子与氙气的碰撞截面数据取自Lxcat网站[13]。

在Δt时间内,目标粒子与背景粒子发生空碰撞的概率可以表示为

P=1-exp(RiΔt)

(10)

则每个时间步长内发生碰撞的最大次数Ncoll=NtotalP,其中Ntotal为模拟中的总粒子数。

通过空碰撞可以避免对每个粒子都进行碰撞的判断和处理,从而减小了计算开销。对于可能发生碰撞的粒子,结合蒙特卡罗方法判断其碰撞类型[14]。

由于全粒子模拟受德拜长度的限制,网格数多且时间步长小,需要采取一定的加速方法来减少计算量。本模型采用了Taccogna提出并已验证可行性的相似设计方法[15],核心思想是人为将放电腔尺寸乘以ξ-1,其中ξ是缩比系数且大于1,同时遵循相似原理,保持主要特征量不变,从而减小计算域中的网格数。缩放后各参数变化情况如表1所示。

表1 相似设计方法参数变化

此外,随着时间的增加,计算域内粒子数急剧增多,为了保证计算效率,引入宏粒子的概念,宏粒子权重表示真实粒子数。由于权重过大或过小都会影响仿真,所以模型中采用粒子自适应权重(APM)的方法来动态调整粒子权重[16-17],实现流程如下。

(1)通过定义每个网格内的理想粒子数Nppc获得第i个网格内粒子的理想权重

(11)

式中:ni为第i个网格粒子数密度;Vcell为网格体积。

(2)当权重小于(2/3)w时粒子被合并以增大权重,当大于1.5w时粒子被分裂。

(3)对于需要合并的粒子,选择与其距离最近的粒子合并。粒子间的距离d为

d2=(xi-xj)2+η2|vi-vj|2

(12)

式中η为距离与速度的比例因子,模拟中设置为1 ps。新形成的粒子速度与原始粒子有一个随机的偏移量,权重为两个原始粒子权重之和,位置可由下式得到

(13)

(4)需要分裂的粒子将被分裂为两个新粒子,它们的速度和位置与原始粒子相同,权重为原始粒子的一半。整体仿真流程如图3所示。

图3 PIC/MCC仿真流程图

1.2 参数设置

本模型的具体参数设置如表2所示。放电腔外加电势一般为上千伏,但为了便于分析,将所有电势均减去阴极电势1 200 V,从而保证阴极电位为0。实验中测得空心阴极发射的初始电子能量大约在2～3 eV[18],仿真中取2 eV;中性粒子的栅极透过率设置为0.3,离子的栅极透过率为0.86。

表2 仿真参数设置

2 仿真结果分析

2.1 进气口位置对等离子体特性的影响

本文选择了图4所示的4种进气口位置,其中双进气口由阴极进气口和主进气口构成。

(a)位置1

因为工质气体是背景气体,所以在运行等离子体程序前,需要采用DSMC方法预先模拟4种工况下中性粒子的运动情况。

中性粒子数密度分布如图5所示:进气口处的粒子数密度最大,单进气口约为2.1×1019m-3,双进气口在1×1020～4×1020m-3范围内,高出单进气口一个数量级;双进气口工况下放电腔出口处中性粒子数密度最小,在2.3×1019～3×1019m-3区间内,单进气口工况下侧壁面中性粒子数密度最小,为1.2×1018m-3。

(a)位置1

以上述中性粒子分布为背景,计算得到离子数密度在放电腔内的分布,如图6所示。阳极壁面的离子数密度最低,约为1×1012m-3,这是由于磁场对电子的约束作用减少了电子对阳极壁面的撞击,碰撞电离主要发生在腔体中部,因此离子也主要聚集在此区域。由图5a知,进气口位置1对应的腔体上游中性粒子密度低,因此电离产生的离子主要集中在放电腔下游,随着主进气口位置靠近下游,离子高密度区也逐渐向下游出口处移动。

放电腔出口处离子数密度分布如图7所示。由图可以看到:双进气口的离子数密度峰值较单进气口偏离了对称轴,这是双进气口工况的中性粒子高密度区偏向阳极壁面所导致的;进气口位置4整体离子数密度最高,进气口位置2和3的密度相差不大,进气口位置1最小;4种工况下最大离子数密度为7.9×1017m-3,平均离子数密度在2.6×1017～4.1×1017m-3之间,与兰州空间技术物理研究所结果的数量级相吻合[19];在径向位置增大至4.5 cm左右时,由于阳极后壁面的存在,离子数密度趋近于0,出口处离子密度变化趋势与文献[3]基本一致。

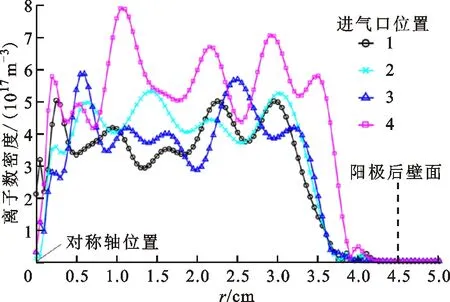
图7 不同进气口位置下腔体出口处离子数密度随径向位置的变化

为了保证离子推力器引出束流的稳定性和准直性,需要保证腔体内尤其是栅极附近等离子体参数的均匀性。用一个区域网格点上的密度与平均密度比值的标准差来衡量该区域粒子分布的均匀度,如下式所示

(14)

通过计算得到腔内的平均电离率和出口处离子均匀度,如图8所示。双进气口工况的平均电离率高于单进气口,进气口位置1的电离率为9.67×1023m-3,进气口位置2最大,为1.1×1024m-3;双进气口工况的离子均匀性差于单进气口,进气口位置1的S=0.65,进气口位置3的离子均匀性最差,S=0.81。

图8 不同进气口位置的平均电离率和离子均匀度

表3对比了推力器的宏观性能,发现双进气口工况的性能优于单进气口,其中进气口位置4最优。4种工况下计算的推力在0.094～0.112 N之间,在文献[20]中所报道的实验数据范围内。

表3 不同进气口位置下推力器的宏观性能

综合来看,进气口位置4既能保证较高的电离率1.07×1024m-3,得到较均匀的离子分布,S=0.69,又能拥有最优的推力器宏观性能。

2.2 阴极位置对等离子体特性的影响

放电腔内的初始电势可以空心阴极前端为界分为两部分,一部分是由于阴极低电势使电场指向阴极,另一部分是由于屏栅低电势使电场指向屏栅,这就可能导致电离产生的离子回流到阴极并被还原为中性粒子,影响推力器效率,因此在设计推力器时就需要考虑阴极位置对等离子体特性的影响。

基于2.1小节的结果,将进气口位置4设定为本节背景气体初始条件,并选择阴极长度lc为3、4、5、6和7 cm这5个工况进行研究。

不同的阴极位置会直接影响电子分布,进而影响出口离子均匀性以及电离率,电子数密度分布如图9所示。由图可以看出:在磁场的约束作用下,只有少数电子撞击到永磁体附近的阳极壁面,从而减弱了对壁面的腐蚀,电子数密度在3.5×1014～1.9×1015m-3之间;随着阴极长度的增加,放电腔上游电子数密度逐渐减小,下游电子数密度逐渐增大。

(a)lc=3 cm

表4为不同阴极位置下腔内的平均电子密度和均匀度。增加阴极长度会降低平均电子密度,极长度过短,又会影响电子在腔内的均匀性,lc在4～6 cm之间是相对较合适的选择。

表4 不同阴极位置下腔内平均电子密度和均匀度

但阴

图10为不同阴极长度下腔内离子数密度分布。由于离子分布主要由电子分布决定,因此其随阴极长度的变化趋势与电子基本一致。由图可以看到,阴极长度为3、4和5 cm的工况中阴极上方区域、阳极前壁面、上游侧壁面离子数密度较高,回流现象较明显。

(a)lc=3 cm

为了对回流现象进行更精确的研究,选取阴极上方区域的离子数密度进行分析,如图11所示。由于阴极长度不同,对轴向坐标进行归一化处理,即

(15)

式中:z*为相对轴向坐标;z为实际轴向坐标。

从图11可以看出,随着轴向位置的增加,阴极上方区域离子数密度整体呈上升趋势,而阴极长度的增加会减小阴极上方区域的离子数密度,但当lc增加到6 cm之后,离子数密度下降趋势不再明显。

图11 不同阴极位置下阴极上方区域离子数密度随轴向位置的变化

图12为放电腔出口处离子数密度分布,可以看到:随着径向位置的增加,出口处离子密度先保持在一定的范围上下波动,而后当径向坐标接近4.5 cm时,离子数密度逐渐减小并趋近于0;5种工况下离子平均密度在2.9×1017～8.9×1017m-3范围内,与文献[19]的数据基本吻合;随着阴极长度的增加,出口处离子数密度逐渐增大,同样当lc增加到6 cm之后,离子数密度基本不再增大。

图12 不同阴极位置下腔体出口处离子数密度随径向位置的变化

图13为5种工况下腔内平均电离率和出口处离子均匀度,可知lc=7 cm的平均电离率最小,为8.74×1023m-3,lc=3 cm的平均电离率最大,为2.54×1024m-3;lc=5 cm的离子均匀性最好,S=0.63,lc=3 cm的离子均匀性最差,S=0.8。

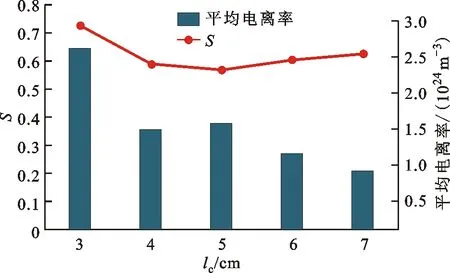
图13 不同阴极位置的平均电离率和离子均匀度

通过对比表5给出的推力器宏观性能,发现阴极长度的增大可以提升推力器的宏观性能。

表5 不同阴极位置下推力器的宏观性能

综合来看:虽然lc=3 cm工况的电离率高出其他工况近1倍,但是回流现象最严重,出口处离子均匀性最差,推力器宏观性能最差;lc=7 cm工况的推力器宏观性能最优,但是其电离率最小,离子分布均匀性较差;lc=4～5 cm的工况内,在保证较好离子均匀性的同时,平均电离率相对较高,且回流现象不严重,推力器宏观性能较好。