具有恐惧效应的Leslie-Gower捕食模型的稳定性
2021-07-13刘俊利
吕 潘,刘俊利
(西安工程大学 理学院, 陕西 西安 710048)
0 引 言
在生态学中,捕食者-食饵的驱动机制是一个重要的研究课题。有2种不同的方法得到捕食者与食饵之间的相互作用对食饵的影响[1]:第1种是捕食者通过直接捕食食饵而影响食饵种群[2];第2种观点是捕食者的存在以及间接行为也会影响食饵的种群。1998年,理论生物学家LIMA认为捕食者的存在会引起食饵的恐惧,而且会改变食饵的一些行为和生理特征,从而影响食饵的种群数量,并且这种影响在一定情况下远远大于直接捕食造成的影响[3]。在恐惧效应下,食饵的很多行为都发生了改变,包括栖息地、觅食、繁殖等的改变[4-9]。虽然食饵对于捕食者的恐惧造成的反捕食行为增加了成年食饵生存的概率,但是从长期来看,这种反捕食行为会影响食饵的物种数量[7]。对于恐惧效应是否可以对食饵的物种数量造成影响,ZANETTE等对其进行实验研究,表明歌雀对捕食者的恐惧导致其繁殖率减少了40%,证明了食饵对捕食者的恐惧会产生一定的反捕食行为,从而使食饵的出生率和存活率减少[6]。
尽管捕食者与食饵之间的动力学行为可以用不同的功能反应函数描述,但是把这些功能反应纳入到捕食者-食饵系统中,也不能反映出恐惧对食饵的种群数量的影响。早期研究认为,捕食者的功能反应为捕食者每单位时间消耗的食饵数量,功能反应仅是食饵密度的函数。最常见的功能反应函数是HOLLING在1965年提出的Holling II型功能反应函数[10]。ARDITI等生物学家认为,功能反应在更大的时间和空间尺度上也可以依赖于捕食者,即捕食模型的功能反应函数与食饵和捕食者的密度有关,提出了比率依赖的功能反应函数[11]。目前,有很多文献研究了具有比率依赖功能反应的捕食者-食饵模型[12-13]。1960年,LESLIE给出了Leslie-Gower捕食者-食饵模型,认为捕食者的生长功能反应不同于捕食者的捕食功能反应,而是取决于捕食者与食饵的比率[14]。文献[15-17]介绍了一类具有Holling及Crowley-Martin型功能反应的Leslie-Gower捕食者-食饵模型,并分析了平衡点以及平衡点的稳定性。
考虑到恐惧效应对食饵种群的影响,WANG等在2016年首次提出了具有恐惧效应的数学模型,建立了具有恐惧效应的线性和Holling II型功能反应的捕食者-食饵模型,并分析了平衡点的稳定性以及Hopf分岔的存在性和Hopf分岔的方向[18]。研究结果表明,恐惧效应对具有线性功能反应的模型的动力学行为没有影响。但是,对于具有Holling II型功能性反应的模型,恐惧效应会以多种方式影响捕食者与食饵之间的相互作用。WANG等假设功能反应仅与食饵的密度有关[18],然而在有的情况下,功能反应与食饵和捕食者的密度都有关系。本文中模型的功能反应为比率依赖型,假设捕食者的增长函数不同于捕食者的捕获项,且假定捕食者的增长依赖于捕食者与食饵的比率。
1 模型的建立
Leslie和Gower[14]提出了如下Leslie-Gower捕食者-食饵模型:
(1)


(2)
式中:k为食饵对捕食者的恐惧因子;p为捕食者的攻击率;m表示半饱和常数。
2 平衡点分析

定理1系统(2)在初始条件x(0)>0,y(0)≥0下存在唯一的解,且解是最终有界的。
证明由系统(2)的第一式可得
x(r-d-bx)
考虑辅助系统
(3)
则有
根据微分方程比较定理可得
故对于任意小的ε1>0,∃T1>0,使得
(4)
由式(4)可得
考虑辅助系统
有
由比较定理可得
因此,对于任意小的ε2>0,∃T2≥T1,使得
综上可得,系统(2)的解是最终有界的。

证明系统(2)的平衡点满足方程
(5)
显然,当r>d时边界平衡点E1存在,下面考虑E2的存在性。由式(5)中第二式得
x=hy
(6)
将式(6)代入(5)中的第一式可得
a2y2+a1y+a0=0
(7)
其中
a2=bkh

3 稳定性分析
定理3系统(2)的边界平衡点E1是不稳定的。

JE1的特征值λ1=d-r<0,λ2=s>0。因此,E1是不稳定的。

证明正平衡点E2对应的雅克比矩阵为
JE2的特征方程为
λ2+B1λ+B0=0
(8)
式中:

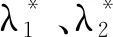


证明对系统作替换,令dt=(x+my)dτ,则系统(2)变为
(9)
因此,系统(2)在第一象限没有正周期解。在定理条件下,平衡点E1不稳定,正平衡点E2局部渐近稳定,因此E2是全局渐近稳定的。
4 Hopf分岔
把系统(2)中的恐惧因子k作为分岔参数,研究在正平衡点E2处出现Hopf分支的可能性。
设λ(k)=λr(k)+iλi(k)为特征方程(8)的特征值,代入方程(8)得
(λr+iλi)2+B1(λr+iλi)+B0=0
将实部与虚部分离得
(10)
在Hopf分岔处应有λr(k)=0。假设k=kH时λr(kH)=0,则由式(10)可得

定理6当k=kH时,若λr(kH)=0,
则系统(2)在平衡点E2处发生Hopf分岔。
下面的定理给出分支周期解的方向和稳定性。
定理7定义L为
gxyfyfx-gyyfx2-
如果L<0,则Hopf分岔为超临界的; 如果L>0,则Hopf分岔为亚临界。其中

考虑系统在(u,v)=(0,0)处的三阶泰勒展开,则有

式中:
其中在(0,0)点处的偏导数分别为
综上可得
式中:
F=(f1(u,v),g1(u,v))T


则
令U=QZ,其中Z=(z1,z2)T,则Z=Q-1U,
式中:
计算第一Lyapunov系数:
将(u,v)替换为(x,y),经计算可得L与定理7中的L相同。由文献[19]可得,若L<0,则在正平衡点E2处发生的Hopf分岔是超临界的;若L>0,则该Hopf分岔是亚临界的。
5 数值模拟
为了分析恐惧效应和Leslie-Gower项在模型(2)中的作用,分别利用参数k、h对系统进行数值模拟。
5.1 系统(2)的全局渐近稳定
考虑参数值(Ⅰ):r=0.13,d=0.003,b=0.02,p=0.01,m=0.54,s=0.19,k=0.43,h=0.06。
在参数值(Ⅰ)下,通过定理5可以得到系统(2)是全局渐近稳定的,如图1所示。
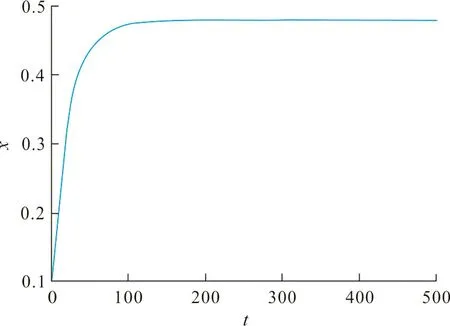
(a) 食饵与时间的关系

(b) 捕食者与时间的关系 图 1 系统(2)达到稳定的状态Fig.1 The graph of system (2) reaching a steady state
5.2 参数k对系统(2)的影响
设定参数(Ⅱ):r=0.8,d=0.003,b=0.02,p=0.46,m=0.54,s=0.19,h=0.49。
在参数值(Ⅱ)下:当k=0.16时,由定理4可知正平衡点是稳定的(见图2);在图3中,参数k=0.43,此时系统(2)的正平衡点不稳定, 系统(2)出现周期震荡。
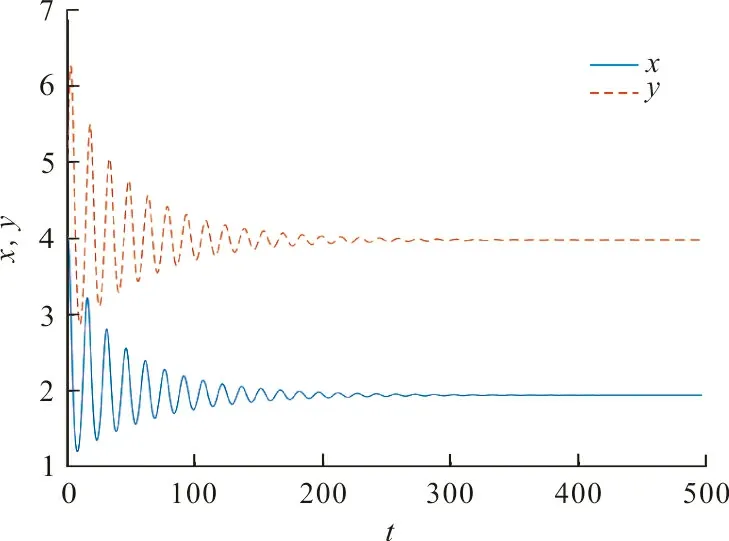
(a) 食饵、捕食者与时间的关系

(b) 食饵与捕食者的关系图 2 k=0.16时,系统(2)的正平衡点是稳定的Fig.2 When k=0.16,the positive equilibria of system (2) is stable

(a) 食饵、捕食者与时间的关系

(b) 食饵与捕食者的关系图 3 k=4.3时,系统(2)在正平衡点周围周期震荡Fig.3 When k=4.3,the system (2) periodically oscillates around the positive equilibria
5.3 系统(2)关于分岔参数k、h的图形

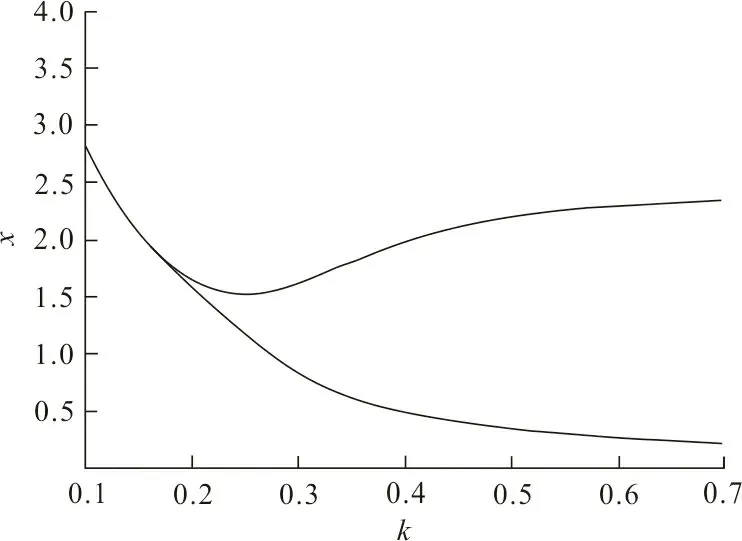
(a) 食饵关于参数k的分岔图

(b) 捕食者关于参数k的分岔图图 4 系统(2)关于参数k的分岔图Fig.4 The bifurcation diagram of the parameter k in system (2)
在数值模拟过程中还发现,参数h对系统的稳定性有一定的影响。利用参数(Ⅱ),得出关于参数h的分岔图形,见图5。通过增加h的值,至h1=0.234时,内部平衡点失去其稳定性,系统(2)出现周期解;当h增加至h2=0.69时,系统(2)又变得稳定;当食饵提供的食物量转化为捕食者的出生量小于0.234时,系统(2)是稳定的,此时食饵与捕食者的数量趋近于某一正常数;当食饵提供的食物量转化为捕食者的出生量为0.234到0.69之间时,系统(2)出现周期解,捕食者与食饵都不是稳定存在的;当食饵提供的食物量转化为捕食者的出生量超过0.69时,食饵与捕食者的数量又趋于稳定水平。

(a) 食饵关于参数h的分岔图

(b) 捕食者关于参数h的分岔图图 5 系统(2)关于参数h的分岔图Fig.5 The bifurcation diagram of the parameter h in system (2)
6 结 语
本文研究了一类具有恐惧效应和比率依赖功能反应的Leslie-Gower捕食者-食饵模型。模型(2)总存在一个不稳定的边界平衡点,在一定条件下,模型(2)还存在一个全局渐近稳定的正平衡点。理论分析表明,恐惧效应对模型(2)的动力学行为有很大的影响:随着恐惧程度的变化,稳定的正平衡点可能变得不稳定,在正平衡点处出现正周期解。数值分析表明:当恐惧程度较小时,系统(2)是稳定的;当恐惧程度超过某一临界值kH时系统又变得不稳定;食饵能量到捕食者能量的转化程度也会影响系统(2)的稳定性。
