基于改进神经网络的降低锭子转速波动控制算法

王延年，宋功庆

(西安工程大学 电子信息学院，陕西 西安 710048)

0 引 言

细纱卷绕作为成纱的最后一道关键工序，细纱的产量和质量都极大影响着纺织厂的效益[1]。通常纱线在卷绕过程中，锭子无刷直流电机转速波动较大，会出现成纱捻度差异较大，捻度不均匀率高，纱线易断头等问题[2]。

针对以上问题，在不升级电锭细纱机设备的前提下，近年来一些学者采取经典PID控制算法让锭子在设定的转速内运行[3-4]。但纱线卷绕过程受细纱张力波动、电机参数变化等因素影响[5-6]，该算法中PID参数不能去实时调整而造成锭子转速波动较大。很多文献都在研究如何准确检测细纱断头[7-8]，并没有深入探讨如何减少细纱断头现象。为此，本文将BP神经网络算法与PID控制器结合，在锭子无刷直流电机运行的过程中，神经网络会对锭子反馈的信息进行学习，从而实时调整PID参数，让电机尽可能地维持在设定的转速运行。但神经网络算法有收敛速度较慢和最优初始权值难以确定等问题，引入搜索空间内PSO算法对这些问题进行优化，克服了BP神经网络的缺陷。让锭子运行过程中转速、转矩波动更小，使纱线成纱捻度差异小，纱线断头减少[9-10]。

1 基于BP神经网络优化PID控制器算法

1.1 经典PID控制器算法

首先计算出系统给定量与反馈量的偏差，再将该偏差进行比例、积分、微分等线性运算，最后得到下一时刻系统所需对应的控制量[11]，增量式的数字PID控制算法表达式为

u(k)=u(k-1)+kp[e(k)-e(k-1)]+

kie(k)+kd[e(k)-2e(k-1)+e(k-2)]

(1)

式中：kp、ki、kd分别为PID控制器的比例、积分、微分系数；u(k)为系统控制量；e(k)为系统误差。

1.2 BP神经网络的PID控制器算法

经典PID控制算法中3个参数值kp、ki、kd在系统运行前就已经设定好，不会随着细纱张力波动、电机参数发生变化而作出相应改变，从而导致电机转速有较大的波动。根据在控制系统中采集到的电机转速、转矩、电流等值，通过BP神经网络学习对PID的3个参数实时调节,以达到减小电机转速波动的目的，进而减少纱线断头的次数，则式(1)可描述为

u(k)=f[u(k-1),kp,ki,kd,
e(k),e(k-1),e(k-2)]

(2)

式(2)可利用神经网络算法进行逼近。

搭建3层结构的神经网络。输入层为电机定子三相电流、转速、转矩等给定的样本值，输出层3个节点的输出值分别对应为PID控制器的3个参数。采用系统设定的转速值与神经网络输出PID的3个参数对应下的电机转速值之间的均方根误差(root-mean-square error，RMSE)，作为评判网络预测性能好坏的指标。首先设置整个网络RMSE期望值，接着进行RMSE计算，最后进行更新权值、阈值等运算。

输出层的输入值ck可表示为

(3)

式中：k=1，2，3；yj为隐含层第j个节点的输出值；wjk为隐含层第j个节点与输出层第k个节点之间的连接权值；bk为输出层第k个节点对应的阈值。

由于在该锭子无刷直流电机控制系统中kp、ki、kd的值都为正值，所以输出层的激励函数取非负的Sigmoid函数，表示为

g(x)=1/(1+e-x)

(4)

得到输出层的输出值dk为

dk=g(ck)

(5)

取RMSE，可表示为

(6)

式中：r(k)为电机控制系统设定转速值；y(k)为电机的实际转速值；m为输入层测试样本的个数。

当该函数值大于设定的RMSE期望值时，神经网络就通过基于梯度下降法的误差反向传播算法进行反向传播[12]，并根据网络中传播误差的实时值不断的调整各个神经元和更新相邻层之间的权值与阈值[13]，更新权值与阈值，得

(7)

wjk=wjk+ηyjek

(8)

式中：wij为输入层与隐含层之间的权值；wjk为隐含层与输出层之间的权值；η为学习速率。

(9)

bk=bk+ek

(10)

式中：aj为隐含层对应节点的阈值；bk为输出层对应节点的阈值；ek为神经网络预测误差。

2 基于PSO算法优化的BP神经网络

2.1 PSO算法

PSO算法中各个粒子均代表极值优化问题一个潜在的解，每个粒子依据自身和群体中其他粒子的历史最优解，不断调整自身的位置和移动速度去寻找最优解。粒子调整自身的速度和位置依据的公式如式(11)和式(12)所示，最终在整个空间中寻找到具有最优解的粒子[14]。

(11)

(12)

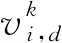
2.2 PSO算法优化BP神经网络

在BP神经网络运算过程中，通过随机函数产生相邻层之间的初始权值，但该初始权值不是最优的，导致网络不能精确预测出电机当前时刻所需对应的PID参数，从而输出的PID参数与实际所需的PID参数有一定的差距，导致电机转速的波动较大。为了降低锭子无刷直流电机转速波动，采用了PSO算法对神经网络算法进行优化，PSO算法能在搜索空间内快速的寻找到具有最优解的粒子[15-16]，PSO算法优化BP神经网络算法的流程图如图1所示。

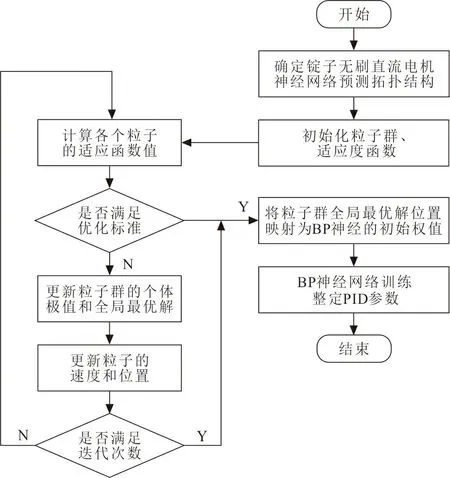
图 1 PSO算法优化的BP神经网络算法流程Fig.1 Back propagation neural network algorithm flow optimized by PSO algorithm

该算法实现步骤：

1) 确定锭子无刷直流电机神经网络预测拓扑结构以及神经网络的学习规则，并初始化粒子群，设定粒子数目和搜索空间维度。

2) 选用BP神经网络相邻层的初始权值和各层阈值映射为粒子群算法中各个粒子的特征量，群体中粒子的适应度函数选用BP神经网络的性能函数均方误差[15]。

3) 当BP神经网络运算输出PID控制器的3个参数时，将这3个参数作为PSO算法中粒子的适应度值，并根据该适应度值不断更新粒子个体和群体的极值。

4) 随着各个粒子的不断迭代进化，粒子的适应度值不断减小，当适应度值变化到设定精度范围内或迭代次数与设定次数相等时终止迭代，此时将粒子群中具有全局最优解粒子的位置向量映射为神经网络的初始权值与阈值。

3 锭子无刷直流电机控制器设计

锭子无刷直流电机速度电流双闭环控制系统框图如图2所示。

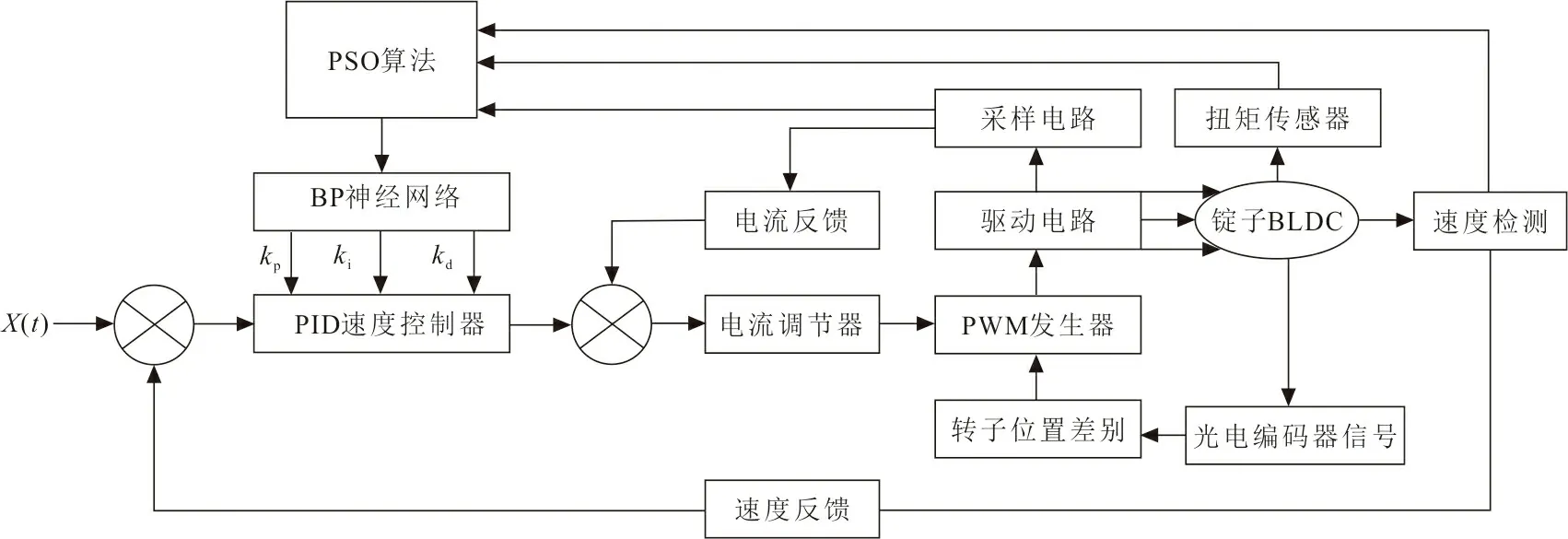
图 2 锭子无刷直流电机双闭环控制系统框图Fig.2 Block diagram of double closed-loop control system for spindle brushless DC motor

图2中，通过光电编码器来获取电机精确的转速及转子位置信息，采样电路采集电机驱动电路的母线电压、电流，定子三相电流、电压等信息，扭矩传感器采集电机的实时转矩值[17-18]。将系统转速设定值与反馈值之间的差值作为PID速度控制器的输入，速度环根据该差值计算出电流环的给定值，电流环将该给定值与当前电机反馈电流值的差值输入到电流调节器中，经过调节后将对应值传给PWM发生器[19-21]。整个控制器在运行的过程中，会根据实时采集到的速度、电流、转矩等信息传递给PSO算法，该算法中各个粒子经过多次迭代不断调整自身位置等操作，最终寻找出在全局搜索范围内具有最优解的粒子，并将该粒子的位置向量映射为神经网络的初始权值和阈值，随后神经网络算法快速拟合电机的非线性控制函数曲线从而获得PID控制器实时最佳的3个参数值[22-23]。

4 结果及分析

4.1 实验平台搭建

该平台由TMS320F28335作为主控芯片的电机控制驱动平台和运行PSO_BP神经网络算法的计算机组成的上位机构成[24-25]。

电机控制驱动平台，其主要功能为根据光电编码器反馈回来的转子位置信号驱动对应开关管，让转子持续转动，接收上位机发送的PID的3个参数，电机驱动板将采集到的信号发送给PSO_BP神经网络。由于该电机的主控芯片计算能力有限，为了更快速实时地计算出不同时刻的PID的3个参数，采用了计算机作为上位机运行PSO_BP神经网络算法，并将运算输出的PID 的3个参数值传送给电机控制驱动平台，这样就实现了对不同时刻PID参数的实时调节。

4.2 实验方法

PSO算法中，初始种群数目选为80，迭代次数选为120，粒子维数选为搭建的神经网络的所有初始权值与阈值之和为128，惯性权重初始值Wstart选为0.8，迭代结束时惯性权重选为Wend为0.3，学习因子c1=c2=2，粒子的速度范围设定在[-4,4]之间。随着粒子的不断迭代，惯性权重值不断减小，起初惯性权重值减小速度慢，此时PSO算法全局搜索能力强，有利于找到具有全局最优解的粒子，当找到具有全局最优解的粒子时，惯性权重值减小速度变快，有利于加快PSO算法的收敛速度。

4.3 实验结果分析

为了验证无刷直流电机用经典PID控制器和PSO_BP控制器控制效果的差异。实验中用经典PID控制器和PSO_BP控制器分别控制无刷直流电机在设定转速2 700 r/min时运行。图3为电机在控制系统设定转速下2种控制器对应的启动状态和稳定运行状态下的转速响应曲线。

(a) 电机启动过程转速响应曲线

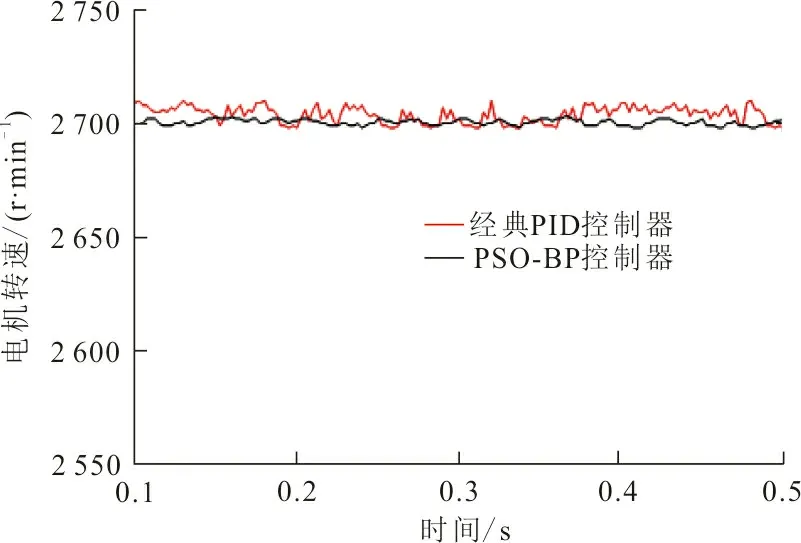
(b) 电机稳定运行转速响应曲线图 3 电机在设定转速下2种控制器对应的转速响应曲线Fig.3 The speed response curve of the two controllers under the set speed of the motor

从图3(a)可知，经典PID控制器相较于PSO_BP控制器控制下电机启动过程转速波动较大，且收敛速度较慢，最大超调量分别为0.26%和0.11%。从图3(b)可知，经典PID控制器控制下电机转速稳定在2 702 r/min，波动范围为2 698～2 707 r/min，平均转速波动为2.73%，PSO_BP控制器控制下电机转速波动范围为2 699～2 703 r/min，稳定在2 700 r/min运行，平均转速波动为0.65%。图4为在电机稳定运行卷绕细纱过程中突遇某处纱线张力较大时，2种控制器对应的转速响应曲线。

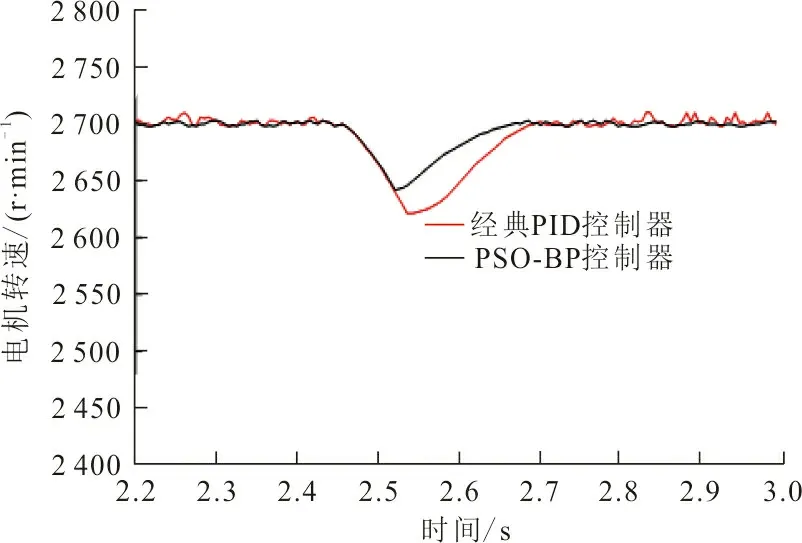
图 4 2种控制器下电机突遇扰动转速响应曲线Fig.4 The speed response curve when the motor encounters disturbance under two controllers

从图4知，电机卷绕细纱过程中突遇一个扰动，PSO_BP控制器相较于经典PID控制器控制下电机响应速度更快，且降低的转速值更小，转速分别下降到2 642 r/min、2 620 r/min，电机从受扰动到恢复到稳定转速所用时间分别为0.19 s、0.23 s。图5为电机在2种控制器下稳定运行时的转矩输出。

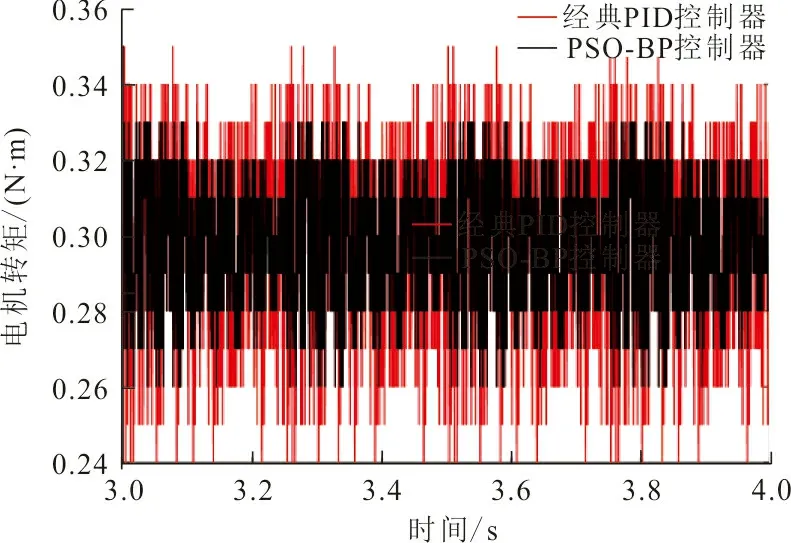
图 5 电机在2种控制器下稳定运行时转矩输出Fig.5 Torque output when the motor runs stably under the control of two controllers

从图5可知，经典PID控制器相较于PSO_BP控制器控制下电机稳定运行过程中转矩波动较大，经典PID控制器控制下电机转矩波动范围为0.24～0.35 N·m，PSO_BP控制器控制下电机转矩波动范围为0.26～0.33 N·m。

5 结 语

为了提高纺织厂细纱产量和质量，从降低电锭细纱机锭子无刷直流电机转速波动角度入手。通过改进神经网络在线实时整定PID参数，采用PSO算法对神经网络进行优化，改善了神经网络在反向传播过程中的缺陷，最终达到了让锭子无刷直流电机在运行过程中转速、转矩波动更小，应对突发扰动响应速度更快。减少了细纱在卷绕过程中的断头次数，纱线的捻度更好，可改善细纱的产量和质量。