静态推靠式旋转导向钻具静力学特性分析*
2021-07-12毕研涛柳贡慧马清明杨宁宁朱杰然刘建勋
毕研涛 柳贡慧 马清明 杨宁宁 朱杰然 刘建勋
(1.中国石油大学(北京)石油工程学院 2.中石化胜利石油工程有限公司 3.北京工业大学 4.中石化胜利石油工程有限公司随钻测控技术中心 5.重庆科技学院机械与动力工程学院 6.重庆科技学院石油天然气装备研究院)
0 引 言
传统滑动导向钻井技术在复杂结构井中作业面临摩阻扭矩大、钻压传递困难及井眼轨迹控制难度大等问题。为此,国内外石油钻井公司自20世纪80年代便开展了旋转导向钻井系统(RSS)研究,并逐步形成了以Schlumberger公司PowerDrive钻井系统、Baker Huges公司AtuoTrak钻井系统及Halliburton公司Geo-Pilot钻井系统为代表的商业化产品[1-3]。
自RSS问世以来,旋转导向钻井系统底部钻具组合(RSBHA)的受力变形分析一直是业内学者研究的热点。赵金海等[4]运用加权余量法建立了RSBHA静力学模型,分析了偏置式RSBHA的力学行为。唐雪平等[5-7]采用纵横弯曲梁法,从静力学角度对变刚度变截面RSBHA的受力问题进行了分析。洪迪峰等[8]以纵横弯曲梁法和有限元法为基础,提出了一种广义纵横弯曲法,建立了RSBHA有限元模型,分析了RSBHA的力学特性。WANG J.等[9]运用有限元法研究了推靠式RSBHA的动力学特性,分析了柔性短节长度和直径对造斜力的影响。冯长青等[10]利用ANSYS有限元软件计算了RSBHA受力与变形特征,着重分析了造斜力的主要影响因素。
以上研究均将RSS导向机构以集中力等效,对心轴-外筒-井壁之间运动约束并未在建模过程中详细考虑。为此,本文根据AutoTrak Curve静态推靠式RSS系统的结构和工作原理,考虑钻柱与井壁接触,引入心轴-外筒-井壁相互作用模型,建立了静态推靠式旋转导向系统底部钻具组合(RSBHA)有限元模型,分析了井眼曲率、导向力和钻压等参数对RSBHA静力学特性的影响,以期为RSBHA系统的井眼轨迹控制预测和力学特性分析提供参考。
1 RSBHA有限元模型建立
为便于分析计算,做如下假设:
(1)井壁轴线为三维光滑曲线,井壁为刚性,其截面为圆形;
(2)忽略钻柱结构和螺纹等局部特征;
(3)初始时刻钻柱与井眼轴线重合;
(4)忽略温度和沉砂影响;
(5)钻井液的黏滞作用与瑞利阻尼等效[11]。
1.1 钻柱单元模型
RSBHA长度通常小于200 m,具有较小的长细比,可视为短梁,其横向剪切应力的影响不可忽略[12]。鉴于此,本文依据Timoshenko梁理论,将RSBHA沿轴向方向离散为一系列具有圆环形截面的弹性均质梁单元,每个单元有2个节点,每个节点具有6个自由度:3个平动自由度和3个转动自由度。梁单元的节点广义位移为[13]:
(1)
式中:u为轴向位移,m;v、w为横向位移,m;θ为角位移,rad;i∈(1,2),为节点编号。
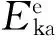
(2)
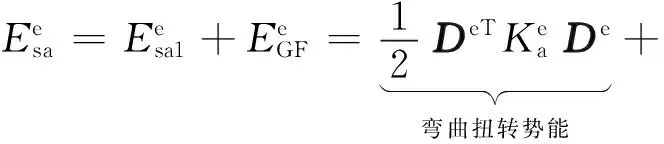

(3)
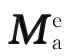
1.2 RSBHA与井壁相互作用模型描述
RSBHA在复杂载荷作用下与井壁发生随机多向接触碰撞,接触位置与接触状态事先无法确定。因此,建立准确有效的模型描述接触行为具有重要意义。处理RSBHA与井壁接触碰撞问题的要点在于接触位置的判断和接触力/摩擦力的计算。为此,将RSBHA与井壁分别视为潜在的“管中管”接触对[14-15],创建接触单元和目标单元并依附于RSBHA的外表面和井壁的内表面上,接触单元与所附着的梁单元满足变形协调条件。
基于RSBHA与井壁的空间构型,判断二者之间的位置关系,求出距离最近的节点位置,可计算出它们之间的距离d:
d=‖xmn-xsn‖
(4)
式中:xmn为井壁轴线上节点的位置矢量,m;xsn为RSBHA轴线上节点的位置矢量,m。
理论上,RSBHA与井壁存在侵入-分离两种状态,而实际上侵入状态不存在。为消除这种可能,引入间隙函数δ来判定二者之间的接触状态。当RSBHA外半径为rb、井筒半径为rpo时,则有:
δ=|rb-rpo|-d
(5)
(6)
(7)
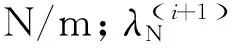
1.3 导向机构有限元模型建立
RSS导向过程中,外筒相对井壁静止,支撑块伸出并与井壁接触,依靠井壁产生的法向反作用力使钻头产生侧切力,进而实现导向(见图1a)。在这一过程中,心轴与外筒、外筒与井壁均构成随机接触,且彼此接触行为相互耦合。为此,本文以Timoshenko梁单元描述心轴、外筒和井壁,将外筒按变截面梁处理为支撑块和非支撑块两部分,于是,心轴、外筒和井壁由三体细化为四体,它们之间构成心轴-外筒、外筒部分-井壁、外筒非支撑块-井壁三层接触。故采用四体三层接触分析模型处理各体之间相互作用(见图1b)。它们之间的随机接触仍采用“管中管”接触单元加以描述。与1.2节类似,首先需要计算各接触对之间的间隙函数:
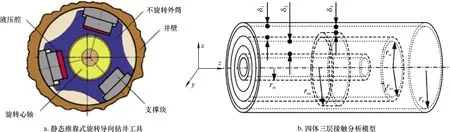
图1 静态推靠式旋转导向钻井工具与四体三层接触分析模型
(8)
式中:rm为心轴外半径,m;rsi为外筒内半径,m;rso为外筒非支撑块部分的外半径,m;rsw为外筒支撑块部分的外半径,m;d1为外筒非支撑块部分的轴线与井眼轴线之间的最小距离,m;d2为心轴轴线与外筒轴线之间的最小距离,m;d3为外筒支撑块部分的轴线与井眼轴线之间的最小距离,m。
然后,根据间隙函数判定各体之间是否发生接触,并计算相应的接触力和摩擦力。
若假设外筒为等截面梁,则本文四体三层接触模型退化为三体二层接触模型。关于三体二层接触退化模型的验证可参考文献[16]进行,这里不再赘述。
1.4 边界条件及模型求解
将RSBHA下端(即钻头处)简化为滑动铰支,并施加钻压,上端视作球铰。将导向力的合力视为横向力,均匀施加在支撑块上。由于外筒相对井壁静止,故仅约束其绕自身轴线的转动自由度和平动自由度,释放其余自由度。依据汉密尔顿原理,通过弹性体Lagrange方程,得出钻柱系统动力学平衡方程:
(9)
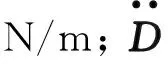
对于非线性方程,本文采用Newmark-HHT法求解[17-18]。若忽略以上模型的动力学效应,施加所有恒载,则可完成静力学特性求解。
(4)慢性肝衰竭 在肝硬化基础上,缓慢出现肝功能进行性减退和失代偿:①血清TBil升高,常<10×ULN;②白蛋白(Alb)明显降低;③血小板明显下降,PTA≤40%(或 INR≥1.5),并排除其他原因者;③有顽固性腹水或门静脉高压等表现;⑤肝性脑病。
2 算例验证
为验证本文提出的RSBHA模型的正确性,分别以纵横弯曲梁法和本文模型分析双扶正器静态推靠式RSBHA的力学特性。RSBHA结构为:ø215.9 mm PDC钻头+ø192.0 mm旋转导向工具×3.17 m+ø214.0 mm扶正器+ø122.0 mm柔性短节×3.17 m+ø178.0 mm钻铤+ø203.0 mm扶正器+ø178.0 mm钻铤若干(为减小扶正器处挠度的影响,近钻头扶正器和上扶正器均取为满眼扶正器)。
其他基本计算参数为:井斜角30°,方位角0°,钻井液密度1.2 g/cm3,导向力合力10 kN,指向高边方向,钻压100 kN。两种方法计算的造斜力和节点位移分别如图2和图3所示。对比可知,两种计算方法得到的结果非常接近,验证了本文所建模型的正确性。
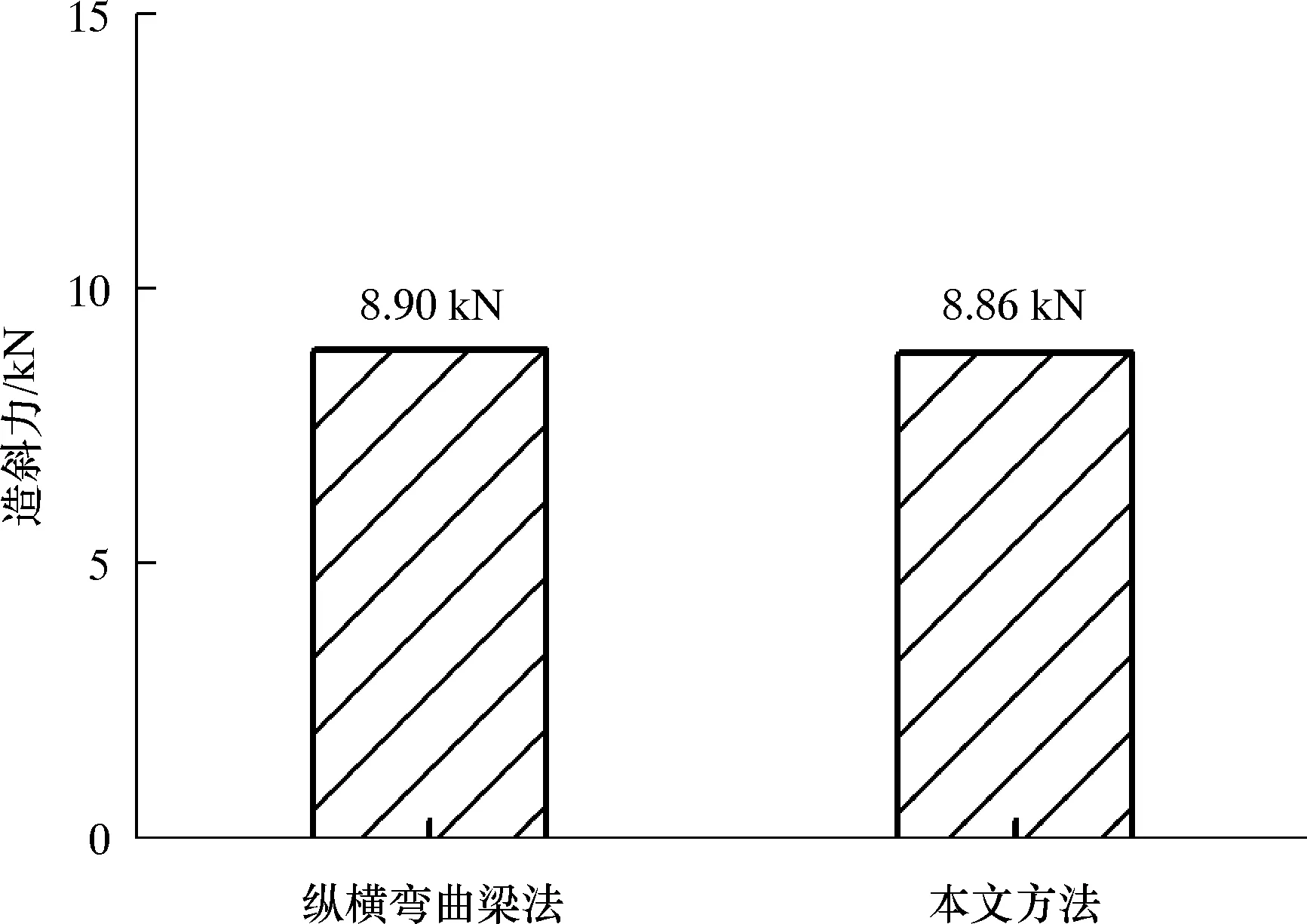
图2 两种方法计算的造斜力比较
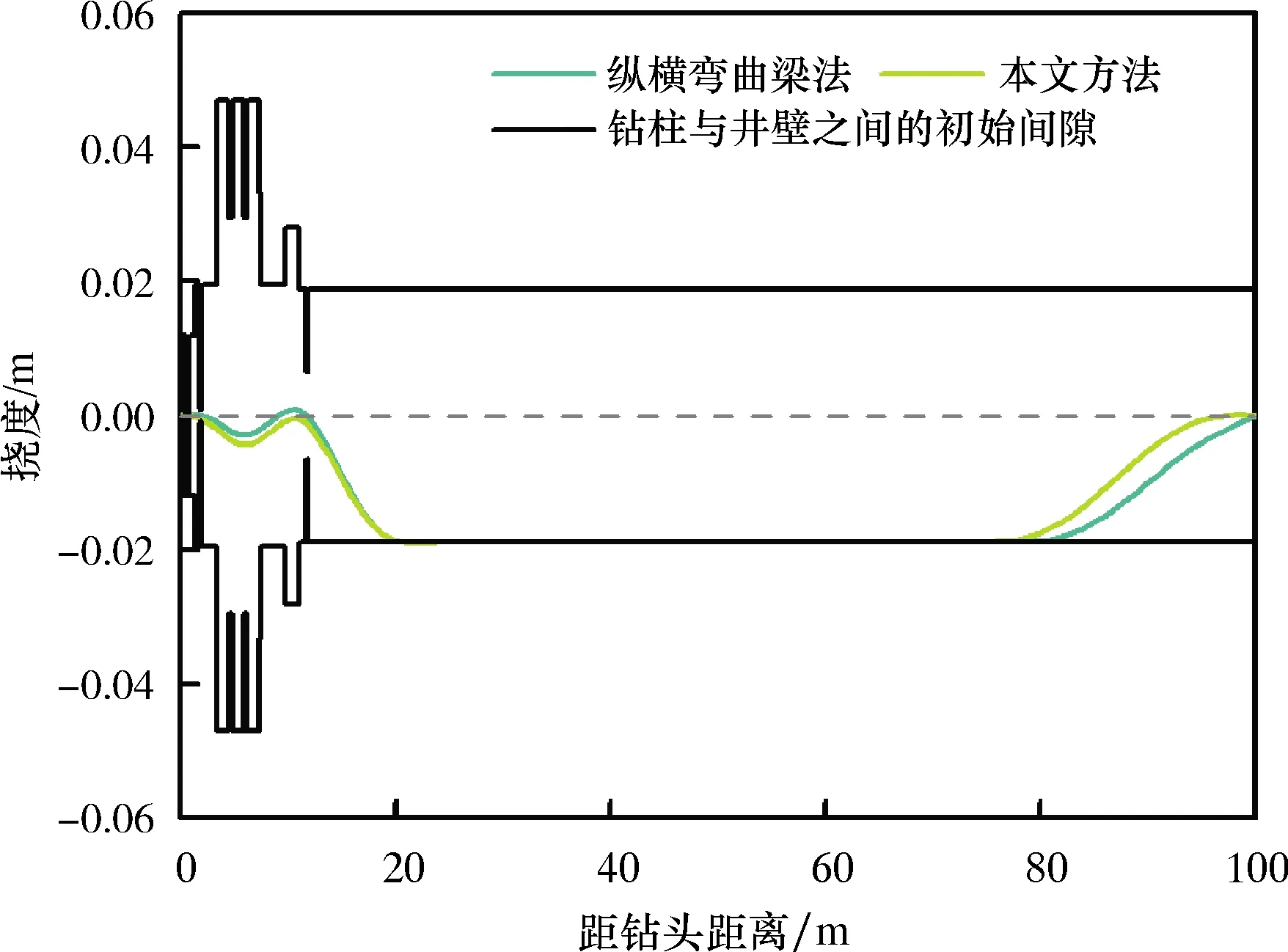
图3 两种方法计算的位移比较
3 应用实例与分析
以双扶正器静态推靠式RSBHA为例,研究井眼曲率、井斜角、导向力和钻压等参数对造斜力等静力学特性的影响。RSBHA结构为:ø215.9 mm PDC钻头+ø192.0 mm旋转导向工具×3.17 m+ø214.0 mm扶正器+ø122.0 mm柔性短节×3.17 m+ø178.0 mm钻铤+ø203.0 mm扶正器+ø178.0 mm钻铤若干。其他基本计算参数为:钻井液密度1.2 g/cm3,导向合力指向高边方向。
3.1 钻压的影响
当每30 m井段井眼曲率为9°、导向力为10 kN时,不同钻压下钻头处造斜力的变化规律如图4所示。
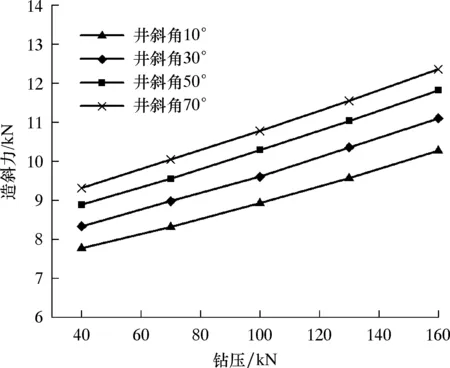
图4 钻压对造斜力的影响
从图4可以看出,当井斜角一定时,钻头处造斜力随着钻压的增大而不断增大,二者之间变化近似呈线性关系。此规律与参考文献[19]中结论一致。例如,在井斜角30°的条件下,钻压由40 kN增大至160 kN时,造斜力由8.33 kN增大至11.10 kN,增幅为2.77 kN,即钻压增大3倍,造斜力仅增大0.33倍。
以上规律表明,实际钻进过程中,虽然增大钻压可以在一定程度上提高造斜力,但增幅并不明显。相反,由于钻压过大会增加钻头因黏滑振动而过早失效的风险,故钻压选择应以减小钻头黏滑振动为宜。
3.2 井眼轨迹参数的影响
当导向力为10 kN、钻压为100 kN时,不同井眼曲率和井斜角下钻头处造斜力的变化曲线如图5所示。
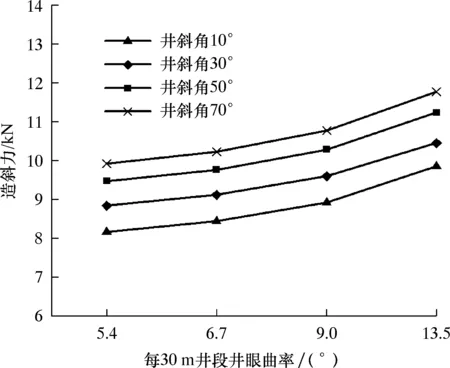
图5 井眼轨迹参数对造斜力的影响
由图5可知:当井斜角一定时,钻头处造斜力随着井眼曲率的增加而逐渐增大,且增大的速率逐渐增大,即井眼曲率越大,静态推靠式RSBHA工具越易增斜,造斜能力越强;当井眼曲率一定时,井斜角越大,钻头处的造斜力越大,这意味着井斜角越大,钻头处造斜力也应越大,如此才能保证按照预设的井眼曲率钻进,这是RSBHA产生的降斜钟摆力随井斜角逐渐增加所造成的。
3.3 导向力的影响
当每30 m井段井眼曲率为9°、钻压为100 kN时,导向力对钻头处造斜力的影响如图6所示。由图6可知,钻头处造斜力随导向力的增大而逐渐增大,二者之间呈线性关系。例如,当井斜角为10°、导向力由10 kN增大至40 kN时,钻头处造斜力由8.92 kN增大至31.01 kN,增幅为22.09 kN,即导向力增大3倍,钻头处造斜力增大2.48倍。
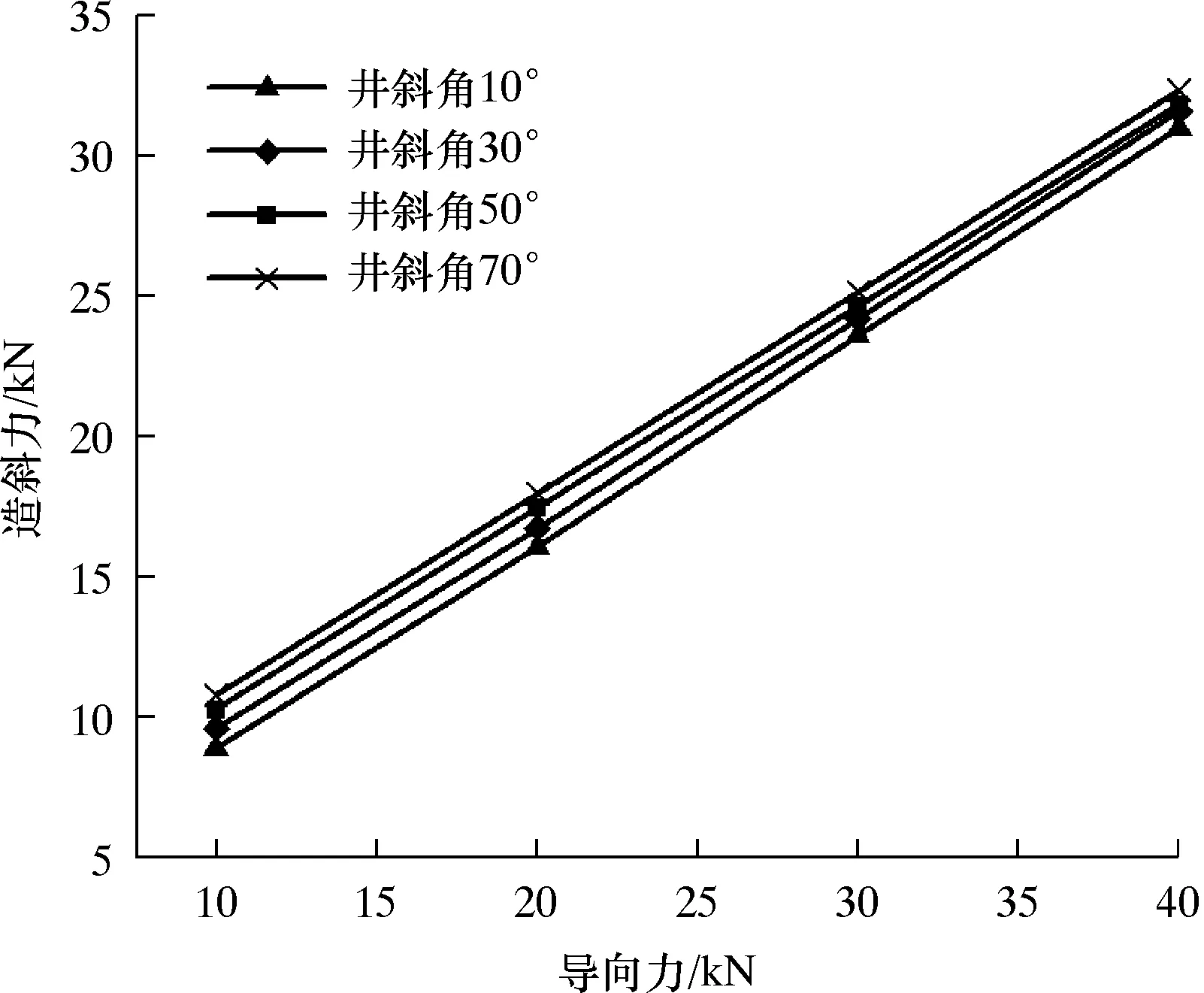
图6 导向力对造斜力的影响
以上分析表明,与钻压和井眼轨迹参数相比,导向力对钻头处造斜力的影响最显著。因此,实际钻进过程中,应优先考虑调整导向力的大小来实现造斜力的控制。
3.4 不同井斜角下钻柱横向位移分布
当每30 m井段井眼曲率为9°、钻压为100 kN时,不同井斜角下钻柱横向位移分布曲线如图7所示(由于导向力与重力均位于井斜平面内,故钻柱变形主要发生在井斜平面内)。由图7可知,随着井斜角的增大,钻柱横向位移也逐渐增大,且井斜角越大,钻柱与井壁之间的接触区域逐渐扩大。上切点随着井斜角的增大逐渐下移,其位置距离钻头22~23 m。这表明选取钻柱长度100 m足以消除上部钻柱对钻头受力的影响。
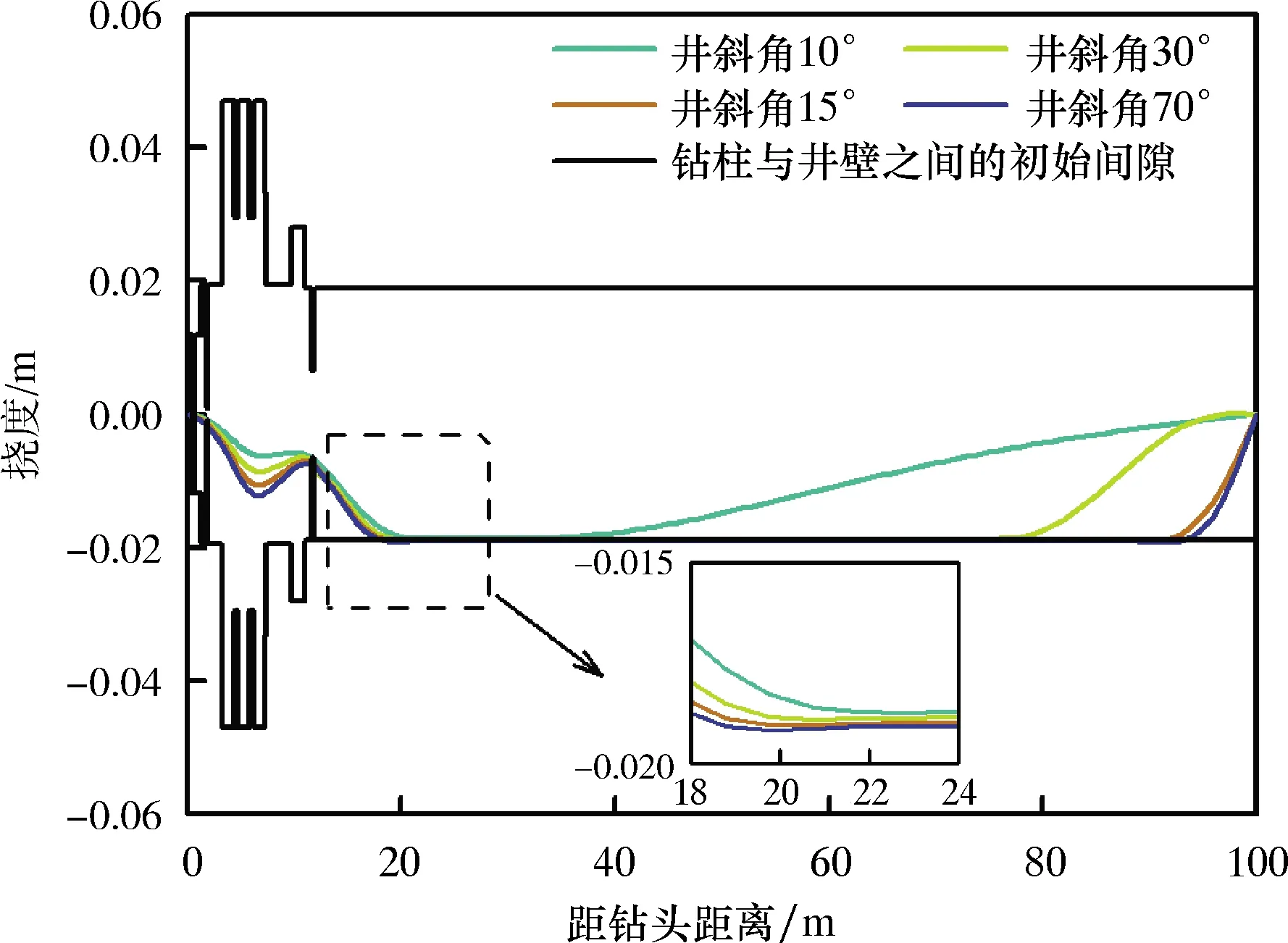
图7 不同井斜角下钻柱横向位移分布(井斜平面)
3.5 不同井斜角下RSBHA与井壁之间接触力分布
RSBHA与井壁间的接触力与摩擦力和磨损量等直接相关,可作为定性评价RSBHA磨损的参考依据。当每30 m井段井眼曲率为9°、钻压为100 kN时,不同井斜角下RSBHA与井壁之间接触力分布曲线如图8所示。由图8a可知,随着井斜角的增大,RSBHA与井壁之间的接触力整体呈增大趋势。接触区域主要集中在支撑块、近钻头扶正器、上扶正器及上部钻铤处,且井斜越大,接触力的幅值越大,接触区域相应增大。进一步分析发现,当井斜角较小时,最大接触力位于支撑块处;随着井斜角的逐渐增加,最大接触力位置逐渐向RSBHA上部转移(见图8b)。
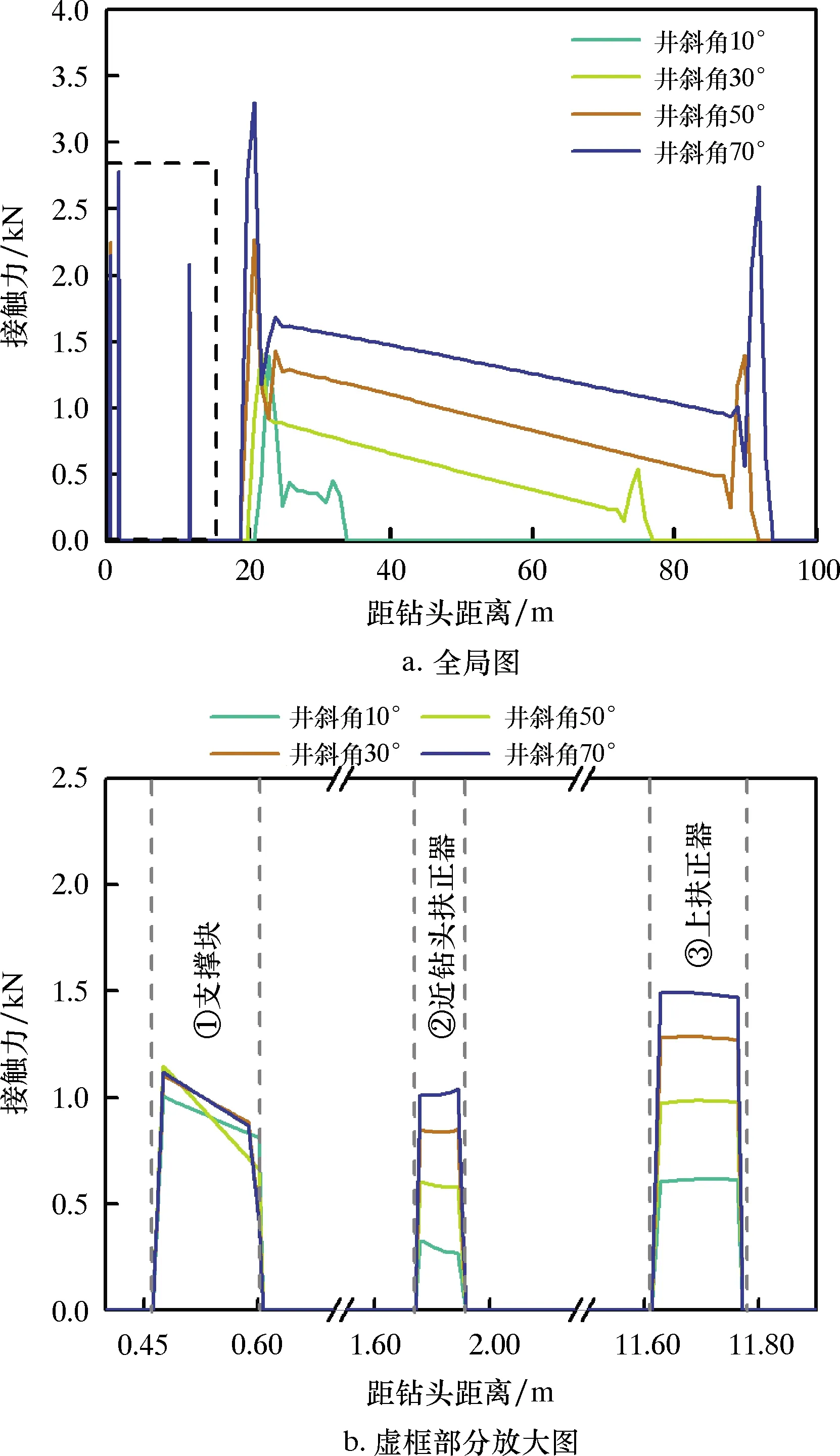
图8 不同井斜角下RSBHA与井壁之间的接触力分布
以上分析结果揭示了造斜过程中接触力随井斜角的变化规律,为判定不同井斜角下RSBHA主要磨损失效区域提供了依据。但由于导向过程中支撑块伸出并与井壁接触,产生较大的接触力,故支撑块在横向方向内并非自由运动,而是受到井壁约束(横向位移近乎为0)。因此在RSBHA力学分析中将支撑块视为扶正器更为合适。
4 结 论
(1)考虑RSBHA-井壁非线性接触及心轴-外筒-井壁的运动约束形式,将Timoshenko梁单元和接触单元相结合,建立了静态推靠式旋转导向系统底部钻具组合有限元模型,给出了数值计算方法。
(2)通过算例对比,纵横弯曲梁法的造斜力与数值解很接近,验证了所建模型的正确性。
(3)井斜角、钻压、井眼曲率、导向力增大均使得RSBHA产生的造斜力增大,其中导向力的影响最为显著。随着井斜角增大,RSBHA横向位移也相应增大,上切点的位置则相应下移,RSBHA与井壁之间的接触力逐渐增大、接触区域逐渐扩大,RSBHA磨损最严重区域由下端向上端逐渐转移。
