高压管汇冲蚀速率数值模拟新方法研究*

2021-07-12李建亭

石油机械 2021年7期

李建亭曾云李宁

(1.中石化中原石油工程有限公司工程服务管理中心 2.长江大学机械工程学院)

0 引言

目前在石油工程领域，致密油和页岩气等非常规油气资源的勘探与开发正愈发受到关注[1-2]。随着非常规油气田开发技术的日益发展，对钻完井压裂领域所需求的装备性能要求也越来越高。压裂液的输送需要高压、长寿命的高压管汇，现有的高压管汇受工作环境的制约[3]，寿命不长成为影响油气开发经济效益的关键因素。影响高压管汇服役寿命的主要因素是冲蚀磨损。国内外学者对管汇冲蚀失效因素进行了多方面分析，压裂液固相物理特性和运动特性是主要因素，管壁材料、内部流场结构、温度及压力等是次要因素[4-5]。

在考虑不同因素影响的情况下，目前关于冲蚀速率的计算还是以半经验计算模型为主，各模型预测的结果都不是很精确[6-11]。数值模拟方法给冲蚀速率的计算提供了新的思路，尤其是计算流体力学离散单元法(CFD-DEM)的发展。以有限元和离散单元法为基础，A.UZI等[12]提出了一维侵蚀模型(ODEM)的概念，描述了粒子壁面碰撞特性的一维流动和统计分布。使用单向耦合DPM模型进行侵蚀预测，忽略了粒子间碰撞的影响[13-15]。对颗粒体积分数较小的流体非常有效，但随着粒子体积分数的增大，其准确性受到了质疑。离散元法(DEM)可以作为欧拉-拉格朗日模型的替代，能够模拟粒子间的相互作用，但计算成本较高。在石油天然气领域中，由于实际流场模拟尺度过大，采用离散元法(DEM)求解时计算工作量巨大，不太适合对流场进行模拟。文献[16]基于Eulerian-Eulerian方法提出了混合颗粒流CFD模型，在侵蚀发生的位置使用拉格朗日模型来准确地跟踪粒子并避免Eulerian-Eulerian方法的不确定性。这种模拟颗粒流的方法是欧拉-欧拉-拉格朗日方法，即DDPM模型，该模型介于DEM和欧拉-欧拉方法之间。目前，随着超深井的开采，对压裂液的要求逐渐上升，普通水基压裂液的含砂体积分数一般在10%左右，而瓜胶压裂液的携砂性能好，含砂体积分数达到20%左右。文献[17]已证实DDPM方法考虑四相耦合，其计算精确度优于DPM模型。

本文基于DDPM模型，考虑颗粒的不同物理特性，对高压管汇不同结构弯头进行冲蚀速率数值模拟分析，以评估高压管汇的服役寿命。所得结论对高压管汇的结构改进以及剩余寿命评估具有理论和工程应用意义。

1 数值模型

1.1 稠密离散相(DDPM)模型

基于标准欧拉多相流模型，本文研究的固相和液相没有温度传递，为非牛顿流体且流体不可压缩流。连续性方程和动量方程如下[18]：

(1)

(2)

式中：α、ρ、v和p分别表示体积分数、密度、速度和压力，下标f表示流体相。

体积分数和速度场根据拉格朗日方法求取，该方法通过将力平衡积分到每个颗粒上来计算每个颗粒的轨迹。颗粒运动轨迹控制方程如下：

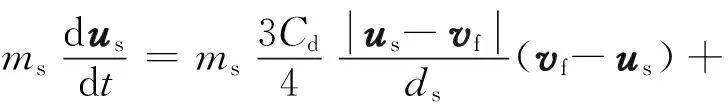
(3)

式中：m为质量，u为速度，Cd为阻力系数，d为直径，FKTGF为颗粒间碰撞和平移产生的力，下标s表示固体颗粒。

式(3)右侧的前3项分别代表阻力、浮力和压力梯度力。传统的DPM方法也考虑了这些力。与DPM模型不同的是，该方法使用颗粒流动力学理论(KTGF)考虑粒子间碰撞和平移的影响。

为了进一步对阻力系数进行定量研究，本文设压裂液支撑剂中存在球形和非球形颗粒，分别采用两种阻力系数经验模型进行分析。针对球形颗粒采用D.GIDASPOW[19]提出的模型，阻力系数Cd的表达式如下：

(4)

式中：Res为颗粒的雷诺数。

(5)

式中：μ为流体的黏度。

对于非球形粒子，采用A.HAIDER等[20]提出的模型，表达式如下：

(6)

式(6)中，各类系数如下：

b1=exp(2.328 8-6.458 1φ+2.448 6φ2)

(7)

b2=0.096 4+0.556 5φ

(8)

b3=exp(4.905-13.894 4φ+

18.422 2φ2-10.259 9φ3)

(9)

b4=exp(1.4681-12.258 4φ-

20.732 2φ2+15.885 5φ3)

(10)

形状系数φ由等效球形颗粒表面积s与非球形颗粒表面积S之比进行求解。与DPM模型不同，DDPM模型考虑了颗粒之间的碰撞力。式(3)中的KTGF模型用于预测颗粒与颗粒间碰撞或者球形颗粒平移产生的应力，表达式如下：

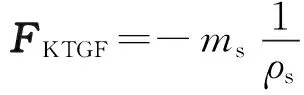
(11)

(12)

μs=μs,col+μs,kin+μs,fr

(13)

(14)

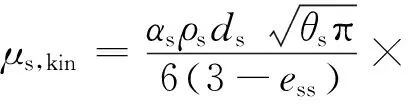
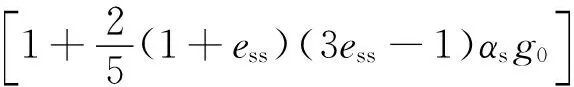
(15)

式中：μs,col、μs,kin及μs,fr分别表示碰撞、运动和摩擦而产生的剪切黏度，ess为粒子碰撞产生的恢复系数，θs为颗粒温度，g0为径向分布函数。

本文研究对象中高压管汇中的颗粒体积分数小于堆积极限，因此忽略摩擦黏度，且计算非球形颗粒时直接等效为颗粒粒径ds。体积黏度λs表达式如下[21]：

(16)

1.2 颗粒之间碰撞受力计算模型

根据文献[22]，颗粒受压力计算的表达式如下：

(17)

颗粒温度的概念基于颗粒的随机平移运动产生的动能，恢复系数默认为0.9。本文主要研究颗粒之间碰撞对冲蚀的影响，其径向分布函数是修正因子，当颗粒变得稠密也就是占比升高时，颗粒之间的碰撞会发生变化，其径向分布函数与颗粒体积占比之间的关系如图1所示。图1中αs,max为颗粒体积分数极限值，取0.63。

图1 径向分布函数与颗粒体积分数之间的关系曲线

2 冲蚀计算模型

2.1 General模型

在冲蚀模型中，本文采用最为普遍的冲蚀速率模型，表达式如下：

(18)

2.2 DDPM冲蚀模型

稠密颗粒流动中，由于近壁面固体颗粒层的屏蔽作用，颗粒间的相互作用可能会影响冲蚀速率，且离散相颗粒即便是几乎平行壁面也同样会导致冲蚀磨损，这样更接近工程实际。本文研究中总冲蚀率Etotal计算式如下：

Etotal=Eabrasive+Eimp

(19)

式中：Eabrasive为固相颗粒对壁面造成的冲蚀，Eimp为考虑屏蔽效应下的颗粒对壁面的冲蚀。

在稠密颗粒流动中，接近壁面的颗粒可能会减速，或者被附近与壁面几乎平行运动的其他固体颗粒反弹。这种屏蔽作用会降低颗粒撞击固体壁面造成的冲蚀率，为考虑这种影响，引入屏蔽因子fshield,计算式如下：

(20)

当局部固相体积分数接近堆积极限(αs,max=0.63)时，壁面将受到保护，不受任何颗粒的冲击，即冲蚀率为0。

3 数值模拟结果分析与讨论

3.1 几何模型和网格划分

结合压裂现场实际工况，高压管汇的内径D=76 mm，进口长度L1=7D、出口长度L2=10D。弯径比一共设置4组(R/D=1.0、1.5、2.0及2.5)，目的是研究不同结构下颗粒轨迹。边界条件选择速度进口和压力出口。

图2为高压管汇几何模型及网格划分图。图2中所有网格采用六面体结构网格，网格尺寸已经过无关性验证。

图2 高压管汇几何模型及网格划分图

本文结合压裂工况不同排量计算，设置支撑剂颗粒密度为2 750 kg/m3，连续相流体选择不可压缩流体，并结合不同工况选用DPM模型和DDPM模型分别进行数值模拟，以便对比分析。表1为不同工况下的参数取值。

表1 不同工况下的参数取值

3.2 不同模型下流场特性分析

在冲蚀磨损研究中，影响因素主要有以下5个方面：①粒子的物理特性和轨迹，②局部的流场和湍流，③固体壁面条件，④多相流的影响，⑤材料磨损造成局部的空穴。在本文的研究中，因素③和因素④在冲蚀模型中已经进行了定义。因此，结合不同工况下定义的参数，主要针对高压管汇的流场特性和颗粒轨迹进行分析。

流场分析中发现，高压管汇的冲蚀失效主要发生在弯头处，因此本研究针对弯头不同偏转角(0°、15°、30°、45°、60°、90°)下弯头截面速度展开分析。在流速12 m/s、质量流量5.14 kg/s、R/D=1.5的工况下，高压管汇弯头处截面云图如图3所示。

由图3可知，在弯头偏转角0°～60°区域可以明显看到流动分层现象，结合伯努利方程可知，弯头内侧压力小于弯头外侧压力，从而形成高速流动区域。在弯头偏转角60°～75°区域可以发现一个现象，即弯头靠近内侧出现了局部流速较小区域，这是一种二次流动现象，随着角度继续增大接近90°，明显出现了低速区域，然后在90°截面后出口直管段，速度在内壁与外壁发生了明显变化。出口直管端靠近外侧的流速明显大于内侧流速，这也说明从弯头区域开始，整个高压管汇以外侧出现冲蚀为主。从湍动能和湍流耗散率的角度来看，在不同的偏转角截面中，靠近弯头内壁的湍动能逐渐增强，湍流耗散率也逐渐增大。这也充分反映在这个区域流动出现了拐点，形成了二次流动。

图3 高压管汇弯头处截面云图

3.3 不同模型下的冲蚀速率对比分析

采用DPM模型和DDPM模型对高压管汇4种工况、4种结构设计开展正交试验，共16组，其数值仿真结果如图4所示。

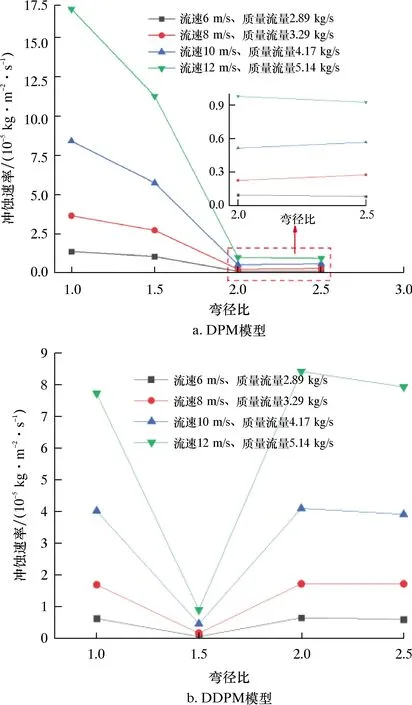
图4 不同模型下高压管汇冲蚀速率模拟曲线

由图4a可知：随着弯径比的增大，冲蚀速率呈递减趋势，弯径比在1.5～2.0时冲蚀速率出现一个相差数量级的下跌，这可能是因为DPM模型计算颗粒运动时主要围绕流体的运动轨迹；随着弯径比的增大，在弯头区域流动比较充分，颗粒在一定程度上接近弯头外侧壁面区域时不会由于速度过快而汇聚集中冲击壁面，这也表明DPM计算方法存在一定缺陷，并未考虑颗粒与颗粒之间的碰撞。由图4b可知，采用DDPM模型时，弯径比在1.0～2.5时，冲蚀速率先减小后上升，R/D=1.5时最小，与DPM模型稍有不同，结合引言中DPM模型的劣势，说明DPM模型在模拟固相体积分数较高的液固两相流时存在一定的偏差。

选择4组工况中流速和颗粒质量流量最小的一组冲蚀云图进行分析，如图5所示。由图5可知：不论是DPM模型还是DDPM模型，在弯径比为1.5和2.0时冲蚀集中位置没有另外几种弯径比明显，且造成的冲蚀面积没有弯径比为1.0和2.5时大，这是因为弯径比较小时，压裂液流经弯头处，其流动方向由于结构变化急促，粒子更容易冲出液相，冲击内壁，造成更为严重的冲蚀磨损；弯径比变大时，在弯头处运动方向改变较为平缓，惯性相对较小，对壁面的冲击较轻，但由于DDPM模型考虑颗粒之间的碰撞，在弯径比过大的区域，汇聚的颗粒增多，颗粒之间的碰撞导致冲蚀速率反而会上升，但随着弯径比继续增大，冲蚀速率呈递减趋势。

图5 不同模型下管汇冲蚀云图对比

3.4 颗粒形状系数对冲蚀速率和冲蚀区域的影响

在高压管汇的弯头处容易形成冲蚀的区域主要为弯头处的外壁和出口直管端的侧壁。图6为4种不同结构下颗粒轨迹图。图6中的流速为12 m/s，质量流量为5.14 kg/s。4种不同结构的颗粒轨迹图皆表明两处区域(弯头外壁和出口直管端侧壁)是颗粒轨迹汇集之处。产生这种现象的原因是：流体从直管进入弯头时存在局部阻力，导致水力动能减小，且3.2节分析过弯头处外壁压力大于内壁压力，内侧壁形成高速流动区域，外侧壁流速相对较低，但外壁区域固相颗粒所受离心力大，导致冲蚀磨损明显增大；在弯头出口直管端由于固相颗粒撞击壁面反弹增多，再加上二次流的牵引作用，导致出口直管侧壁也容易形成冲蚀严重区域。

图6 4种不同结构下颗粒轨迹图

为了进一步研究固相颗粒的物理特性，分别设置0.9、0.7、0.5和0.3共4种不同的形状系数来分析颗粒形状系数对冲蚀速率和冲蚀区域的影响，结果如图7所示。由图7可知，随着颗粒形状系数的减小(颗粒逐渐变得尖锐)，弯头部分的最大冲蚀速率呈递增趋势，本工况速度10 m/s，质量流量4.17 kg/s，弯径比1.5。颗粒的形状系数从1.0减小至0.3时，最大冲蚀速率从5.726×10-5kg/(m2·s)增大到7.79×10-5kg/(m2·s)。由图7可以发现，在弯头截面偏转角为86°～88°时，也就是靠近弯头和出口端直管的交汇处冲蚀速率最大。由图7可以发现一个现象，当固相颗粒形状系数大于0.5时，冲蚀速率随着弯头截面偏转角的增大而增大，但当固相颗粒形状系数小于0.5时，在偏转角15°～45°之间，冲蚀速率呈现递减的趋势。其原因可能是偏转角15°～45°这段区域的外壁内压大，且由于形状系数小固相颗粒的拖曳力系数大，颗粒与流体的跟随性很好，颗粒被流体带着绕过障碍物，而不是撞击壁面，颗粒与壁面的碰撞概率减小，产生了一定的撞击迟缓效应。

图7 颗粒形状系数对冲蚀速率和冲蚀区域的影响

3.5 颗粒斯托克斯系数对冲蚀速率的影响

高压管汇输送的压裂液具有高密度和高黏度(曳力系数考虑黏度的影响)等特性，可对固相颗粒的运动以及冲蚀产生一定影响。与颗粒气流相比，当颗粒体积分数较高时，颗粒载荷对流场的影响通常变得很重要，为此引入一个无因次量——颗粒斯托克斯系数(St)来研究固相颗粒对高压管汇的冲蚀行为，以探索流场与固相颗粒特性之间的复杂耦合效应。St定义为颗粒响应时间与流体流动时间的比值，表示如下：

(21)

当St>1，粒子对时间的响应远不及流体传播对时间的响应，因此有足够的时间来存储粒子以响应流场的变化，并且它们可以紧随流体的流动；当St<1时，情况恰恰相反，粒子将独立于流体而运动。为了研究颗粒的斯托克斯系数对冲蚀的影响，设置固相颗粒为单一直径(0.25 mm)，质量流量为0.7 kg/s，流速为3、6、9和12 m/s。根据式(21)计算得St分别为0.413 7、0.827 4、1.241 1和1.654 8。图8为不同St下冲蚀率云图。

图8 不同颗粒斯托克斯系数下冲蚀率云图

由图8可知：当St<1时，主要冲蚀区域在弯头靠近出口直管端两处侧壁，这是因为一部分颗粒随二次流作用对侧壁造成了冲击磨损；当St>1，二次流对颗粒的影响作用逐渐减弱，固相颗粒主要受惯性力，颗粒动量能克服湍流涡团的影响，流场对颗粒的作用减弱，所以主要冲蚀区域集中在弯头外壁。图9为不同St下颗粒轨迹、流场轨迹及速度矢量对比图。从图9可以看到，当固相颗粒斯托克斯系数小于1时，颗粒轨迹和流场轨迹明显不同，固相颗粒在弯头出口靠近侧壁区域随着二次流形成了复杂的冲击和反弹轨迹，这也是弯头出口直管端两处侧壁区域形成主要冲蚀的根本原因。