路堤下高强度桩复合地基失稳破坏模式判别方法

陆清元

（中铁二十三局集团有限公司 四川成都 610072）

1 引言

高强度桩复合地基是指以具有较高抗压抗弯强度的黏结材料桩作为竖向增强体的复合地基。由于其能显著提高地基承载力、减小沉降变形、增强地基稳定性，在路基工程软基处理中得到了广泛应用[1－2]。然而，即使采用高强度桩加固软弱地基，路堤地基失稳工程事故也时有发生[3]96，主要是由于当前对高强度桩复合地基失稳破坏特性认识尚不成熟，尤其是国内外相关规范中缺乏高强度桩复合地基破坏模式判别方法。因此，建立适用于路堤下高强度桩复合地基失稳破坏模式的合理判别方法尤为必要[4]。

目前，国内外关于路堤下高强度桩复合地基破坏模式的研究具有代表性的是天津大学郑刚课题组[5－7]及日本 Kitazume 团队[8－9]。通过数值分析和离心模型试验等手段，研究了路堤荷载、地基条件、桩身材料特性、桩端锚固深度等影响因素对高强度桩复合地基破坏模式的影响，得到了较为一致的结论，即路堤下桩体复合地基发生失稳破坏与桩体抗弯能力有关，当桩体抗弯强度较高时，桩体易发生整体倾斜破坏；当桩体抗弯强度较低时，桩体易发生弯折破坏。另外，对于极弱土中短桩，若滑动面位于桩端之下，桩体的抗滑贡献得不到发挥，表现为桩端下土体发生剪切破坏。

上述研究成果对于认识路堤下高强度桩复合地基破坏模式具有重要意义，但由于高强度桩复合地基破坏模式影响因素较多，目前还没有相关破坏模式的判别方法。为此，本文综合考虑地基条件、桩身材料抗弯能力、滑面下锚固深度等复合地基稳定因素，基于滑动面上桩身材料抗弯能力与滑动面下桩前土体抗滑力矩间的大小关系，建立高强度桩复合地基桩端滑移、桩体倾斜和桩体弯折破坏模式的判别准则和控制条件，以期为路堤下高强度桩复合地基稳定设计提供依据。

2 路堤下高强度桩复合地基典型破坏模式

（1）桩端滑移破坏

若桩身长度小于滑动面深度，失稳滑面位于桩端之下时，此时桩体全部位于滑面之内，桩体发生水平向滑移破坏，其破坏模式表现为图1中滑面内桩与桩间土沿水平面发生整体移动。

图1 路堤下高强度桩复合地基典型破坏模式

（2）桩体倾斜破坏

当桩体强度及抗弯刚度较高时，桩身极限抗弯能力足以抵抗桩后土体产生的滑动力，桩体将发生侧向倾斜破坏，具体表现为桩与桩间土沿某一方向同时发生侧向倾斜，破坏模式如图1所示。

（3）桩体弯折破坏

若桩身长度大于滑面深度时，滑面下地基土对桩体提供抗滑锚固力，当桩体强度及抗弯刚度较低时，桩后土体产生的滑动力矩大于桩身极限抗弯能力，桩体易发生如图1所示的桩体脆性弯折破坏。

3 高强度桩复合地基破坏模式分析及判别方法

3．1 滑动面上桩后土体产生的滑动力矩

地基失稳时桩后土体对桩体施加主动土压力，从而引起桩身被动受力。对于具有较高材料结构强度的素混凝土桩、CFG桩等高强度桩，桩身材料极限弯矩MU可以抵抗侧向土压力产生的滑动力矩MD。取极限稳定状态分析，即路堤发生整体失稳的一瞬间，所有桩体均沿最危险滑动面发生弯曲破坏，此时桩后侧向土压力产生的下滑力矩达到桩身材料极限弯矩，即MD＝MU。桩身极限抗弯强度MU可根据《混凝土结构设计规范（2015版）》（GB 50010—2010）[10]按式（1）进行确定。

式中：γ为桩截面抵抗矩塑性影响系数；ftk为混凝土轴心抗拉强度标准值。W为桩弯曲截面系数，矩形W＝lb2／6，b为沿弯矩作用方向的边长，一般b为长边，l为短边，圆形 W ＝πd3／32。h 为截面高度（mm），当 h＜400时，取 h＝400，当 h＞1 600时，取 h＝1 600；对圆形、环形截面，取h＝2r，其中r为圆形截面半径或环形截面外环半径。γm为桩截面抵抗矩塑性影响系数基本值，矩形截面取1.55，圆形或环形截面取1.6～0.24r1／r，其中r1为环形截面的内环半径，圆形截面取r1＝0。

3．2 滑动面下桩前土体提供的抗滑力矩

为保证桩体复合地基稳定承载，设计时不仅要保证桩体结构安全稳定，还要保证桩周土体不发生剪切破坏，地基横向容许承载力不应低于桩前被动土压力和桩后主动土压力之差。当地面无横坡或横坡较小时，地基y点的横向容许承载力按式（2）进行计算。

式中：[σH]为地基横向容许承载力；σa、σb分别为桩后主动和桩前被动土压应力；γ、c、φ分别为滑动面下土体的重度、黏聚力和内摩擦角；L为滑动面与桩身交点距地基平面间的距离；y为滑动面至计算点的距离。

对于滑动面以下的桩体部分，对桩底求矩可得到如式（3）所列的滑动面下桩前土体横向抗滑力矩MS，计算模式如图2所示。

图2 滑动面下桩前土体横向抗滑力矩计算模式

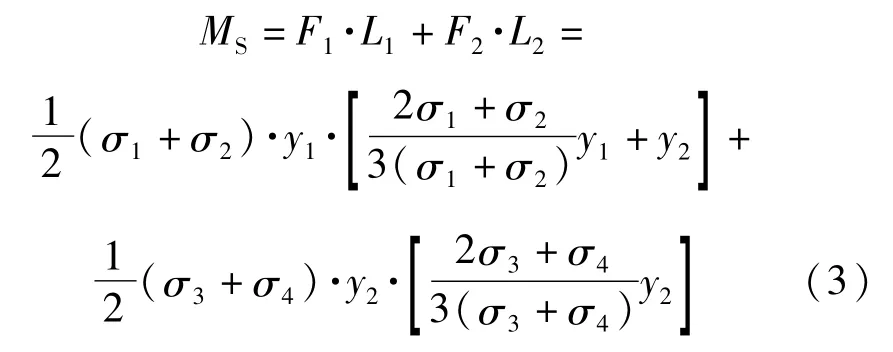
式中：σ1、σ2、σ3、σ4分别为深度 L、y1（桩间土参数）、y1（持力层参数）、y2处桩前土体的横向容许承载力，可按式（4）～式（7）进行计算。

考虑到桩体与桩周土之间存在一定的间隙，因此在计算桩前土体横向抗滑力矩MS时，横向承载力取容许横向承载力的 1／3，即 σ1＝ [σH]1／3、σ2＝[σH]2／3、σ3＝[σH]3／3 和 σ4＝[σH]4／3。

将式（4）～式（7）代入式（3）即可得到滑动面下桩前土体横向抗滑力矩MS。

3．3 高强度桩复合地基破坏模式判别方法

路堤下高强度桩复合地基失稳破坏模式受地基条件、桩身材料抗弯能力、滑面下桩体锚固深度等因素的影响。通过对比滑动面上桩身材料抗弯强度提供的滑动力矩与滑动面下桩前土压力提供的抗滑力矩大小，构建了路堤下高强度桩复合地基桩端滑移破坏、桩体倾斜破坏和桩体弯折破坏的判别准则和控制条件，即：

（1）当桩身总长度小于或等于滑面深度，即h≤L时，路堤下高强度桩复合地基失稳破坏模式为桩端滑移破坏。

（2）当桩前土体横向抗滑力矩MS大于桩身极限抗弯强度MU（MS＞MU），路堤下高强度桩复合地基破坏模式为桩体倾斜破坏。

（3）当桩前土体横向抗滑力矩MS不大于桩身极限抗弯强度MU（MS≤MU），路堤下高强度桩复合地基破坏模式为桩体弯折破坏。

4 工程案例分析

4．1 CFG桩复合地基失稳工程案例

东南沿海某高速铁路DKXX＋673.82～DKXX＋810路基段处两座山体边缘，基底为斜坡状态，采用C15强度CFG桩进行软基加固，加固宽度为路堤坡脚外1.5 m。复合地基设计参数为桩径0.5 m，桩间距1.6 m，正方形布置，桩长9.5～13.5 m，桩顶铺设0.6 m厚碎石垫层，垫层内铺设一层土工格室。

路基设计填土高度9.5 m，实际填土高度约5.9 m（含工作垫层）时，路基顶面发现细小裂缝转而右侧发生坍塌。坍塌从路基中心开始，右半幅向线路外侧整体滑移坍塌，事后开挖调查发现，该CFG桩复合地基承载力检算符合规范要求，失稳破坏由桩体弯折破坏所致，如图3所示[3]96－102。

图3 DK XX＋790段路堤坍塌及开挖现场

4．2 计算模型及参数

基于工点案例，建立了相应的稳定分析模型，模型剖面如图4所示。计算模型中路堤高度5 m，路基面宽度24.6 m，各土层厚度、土体重度、土体抗剪强度指标c、φ取现场勘察参数。需要说明的是1＃、2＃和3＃桩嵌入强风化凝灰岩深度很小，对地基整体稳定性影响可以不计，计算时忽略了该土层所提供的抗滑效应。

图4 计算模型剖面（单位：m）

4．3 结果分析及验证

基于建立的计算模型，采用二维极限平衡瑞典条分法进行路堤下CFG桩复合地基稳定性计算，计算结果合理性在于滑动面的确定。为得到真实的CFG桩复合地基失稳破坏危险滑动面，首先以无桩天然地基危险滑动面为基础，根据滑动面确定滑动面上部各桩初始桩体长度L，进而将滑面上部桩体抗弯强度转化为滑动面上桩体等效抗剪强度；然后将各桩等效抗剪强度赋值再进行第二次计算，即可得到新的滑动面及各桩新的等效抗剪强度。以此类推，直至前后两次得到的路堤稳定安全系数基本一致时即可得到真实的滑动面。通过计算发现，第3次和第4次得到的稳定安全系数均为0.617，取第3次计算得到的滑动面来进行复合地基破坏模式的判断，结果如表1所示。

表1 CFG桩复合地基破坏模式判别计算结果

从表1可以看出，1＃～12＃桩桩前土体横向抗滑力矩MS均远大于桩身极限抗弯强度MU，根据本文提出的高强度桩复合地基失稳破坏判别方法，该复合地基失稳为桩体发生弯折破坏所致，这与工程案例现场开挖桩体弯折破坏结果相一致，表明本文提出的路堤下高强度桩复合地基失稳破坏判别方法的合理性。

5 结束语

基于高强度桩复合地基易发生的桩端滑移、桩体倾斜和桩体弯折破坏等三种典型破坏模式，提出路堤下高强度桩复合地基失稳破坏模式判别方法，并形成以下结论：

（1）根据地基条件、桩身抗弯能力、滑面下锚固深度等因素对复合地基稳定性影响机制，实现了路堤下高强度桩复合地基桩端滑移、桩体倾斜和桩体弯折等三种典型破坏模式的划分。

（2）基于滑动面上桩身材料抗弯能力与滑动面下桩前土体抗滑力矩间的大小关系，建立了路堤下高强度桩复合地基桩端滑移破坏、桩体倾斜破坏和桩体弯折破坏模式的判别准则和控制条件。

（3）基于某高速铁路CFG桩复合地基失稳破坏工程案例，验证了提出的路堤下高强度桩复合地基破坏模式判别方法的合理性，可为路堤下高强度桩复合地基稳定设计提供依据。