盾构隧道施工地表沉降监测与Peck公式变形预测分析

宋新海

（中铁十九局集团第五工程有限公司 辽宁大连 116000）

1 引言

城市地下综合管廊将通水管道、通信管道、供热管道、天然气管道等[1]工程管道集成至地下的隧道之中，并设置专门的检查通道以方便检修，可以保证在不影响交通的情况下对不同的管线管道进行维修，为生活及交通提供了极大便利。地下综合管廊采用盾构法施工具有掘进速度快、使用方便等特点，但盾构法施工对岩土体形成扰动，尤其对于周围土体的沉降影响较大。目前国内外通常使用经验公式法[2－3]、数值分析法[4]、模型试验法[5－6]及神经网络法[7－8]对盾构施工沉降进行预测[9]。段绍伟等[10]利用修正后的Peck公式，对长沙地铁隧道施工过程中产生的地表沉降值进行预测研究，取得了较好的效果。郭二新[11]利用Peck公式对常州市地铁隧道施工引起的地表沉降进行了相关研究。Mair等[12]通过对隧道开挖造成的沉降槽进行分析研究，得出了沉降槽满足高斯分布的结论，并提出黏土地基沉降槽的计算方法。

本文基于某城市地下综合管廊项目D1-D2区间盾构隧道的现场监测数据，对Peck公式运用最小二乘法进行拟合，得出适用于该地区盾构施工的地表沉降槽宽度系数i和地表沉降最大值Smax的取值范围，为该地区相同地质条件下盾构施工进行地表沉降预测提供参考。

2 对Peck公式回归分析

2．1 Peck经验公式

隧道掘进过程中引起的断面沉降，Peck公式认为其近似符合正态分布曲线[9]（见图1），且假定地层损失量Vs与沉降槽体积VL相等。

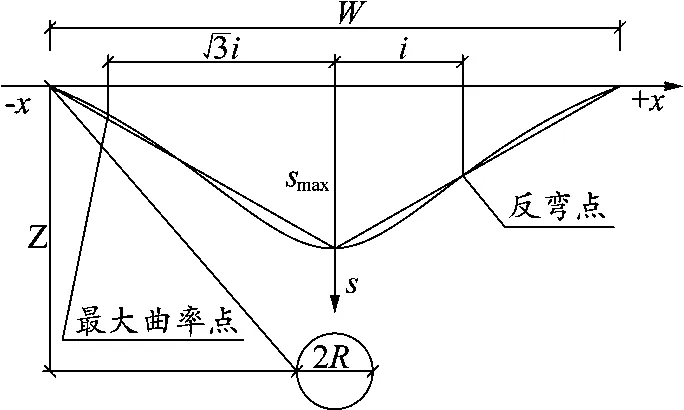
图1 隧道地表横向沉降曲线

横向地表沉降量预估公式及最大沉降量计算公式：

式中：S（x）为距隧道中心轴线x处的地面沉降；Smax为隧道正上方地表最大沉降量；Vs为盾构隧道单位长度的地层损失量；i为地表沉降槽宽度；φ为土体内摩擦角。

2．2 曲线拟合最小二乘法原理

在对数据进行分析时，常会对数据（xi，yi）（i＝0，1，…，m）的关系进行相关性研究，即对给定的自变量 x及因变量 y进行函数关系 y＝s（x，a0，…，an）（n＜m）的拟合，则此时ai为相关因子。因数据之间误差的存在，且相关因子ai的个数少于数据个数（n＜m），其与差值问题不同。该类问题的解决，往往不需要所有的数据点通过 y ＝s（x）＝s（x，a0，…，an），只需给定的点 xi误差值 δi＝ s（xi）－ yi（i＝0，1，…，m）的平方和最小，当 s（x）∈span｛φ ，φ ，…，01φx｝时，则有：

此时，φ0（x），φ1（x），…，φx（x）∈C[a，b]为线性无关函数群，假设[a，b]上存在对应的数组｛（xi，yi），i＝0，1，…，m｝，a≤xi≤b，和对应权值，其中 ρi＞0 为权系数，为求得使 I（an，a1，…，an）最小的函数 s（x）＝span｛φ0，φ1，…，φn｝，则有：

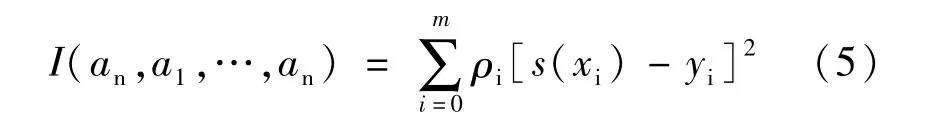
则该方法为最小二乘逼近法，由该方法得到拟合曲线y＝s（x），该方法被称为曲线拟合最小二乘法。式中 I（an，a1，…，an）为 an，a1，…，an的多元函数，若求取I最小值，只需对多元函数I求取极值，则有：

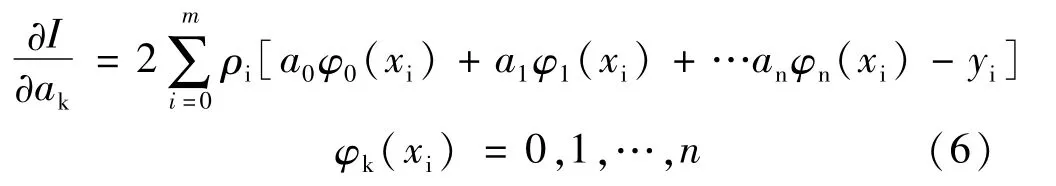
依据内积定理，引入带权内积记号，则有：

则公式（6）可表示为：

公式（8）中关于 a0，a1…an的线性方程组，也可表示为矩阵：

当｛φj（x） j＝0，1，…，n｝为线性不相关时，且点集 X ＝ ｛x0，x1，…，xn｝（m≥n）上则最多存在 n 个不同零点，此时 φ0，φ1，…，φn在 X 上满足 Haar条件，故此矩阵（9）存在唯一解。记为：

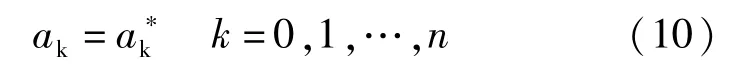
则最小二乘法拟合曲线（11）：

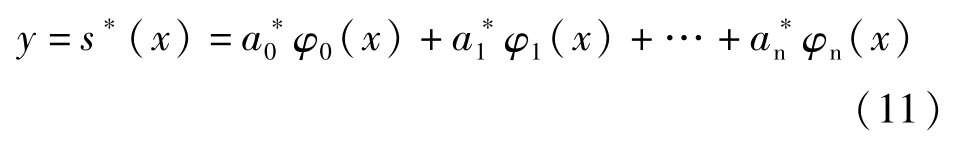
2．3 监测数据线性回归分析

对Peck曲线进行最小二乘法线性回归分析，可得：

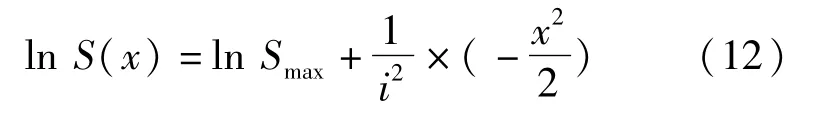
最终得到线性回归方程：

由式（13）～式（18）可以得到回归后的 Smax和i，即：

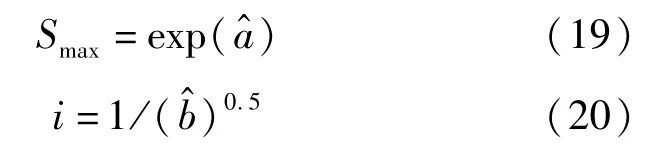
设R为线性回归方程的线性相关系数，则：

当Peck曲线具有较高拟合度时，其线性相关系数｜R｜＞0．8，即可用 Peck曲线预测地表沉降；当Peck曲线拟合度较低时，其线性相关系数｜R｜＜0.3，即该地区的沉降不适用Peck曲线进行预测；其他情况则为中度相关。

3 地下综合管廊盾构区监测点布置

该城市地下综合管廊工程，起于和平区南运河文体西路，止于大东区善邻路。管廊设计采用平行双洞式建筑结构，盾构法施工，管廊内径为5.4 m，盾构开挖直径为6.2 m，平均地下埋深为20 m。管廊沿南运河附近的道路沿线分布。该工程区间场地土层主要为中密实砂土层，地下水条件为第四系孔隙潜水，没有连续的厚层隔水带。

根据监测设计规范要求，需在初始段100 m范围内和吊出井端部100 m范围内，每间隔20 m设置一个监测断面，其他段每间隔30 m设置一个监测断面，监测点布置如图2所示。监测点依据《城市轨道交通工程监测技术规范》（GB 50911—2013）要求进行布置，采用φ20以上的钢筋打入地基土稳定土层中，使钢筋与土层保持稳定，保证钢筋不会因为土层沉降而发生位移。为防止车辆对监测点造成影响，钢筋顶部低于路面5～10 cm，并设置套管保护，如图3所示。

图2 横断面监测点布置（单位：mm）

图3 地表沉降观测点埋设

使用高精度水准仪，对附近的水准点及基准点联测得到初始高程。测量过程中，对测点各项限差进行严格控制，每次读数高差不大于0.3 mm，不在同一水准线上的测点，不超过3个。首次测量，应连续两次对测点进行回测，且两次高程差应小于±1.0 mm，并取其平均值作为测量初始值。

4 盾构施工区地表沉降预测

4．1 横向地表沉降分析

选取5个监测断面的监测数据，对沉降曲线进行拟合，如表1所示。

表1 断面沉降数据转换

续表1

将表1各断面监测数据代入式（12）～式（18）对各监测断面进行回归分析，则可得表2结果和各断面回归后的线性回归函数。

表2 各断面参数值

各断面回归后的线性方程：

将5个断面的实测数据与回归后的线性方程制图进行对比，见图4。由图4和表2可知：断面ZK0＋170、ZK0＋200、ZK0＋230和ZK0＋260四个断面的线性相关系数R均大于0.8，拟合度较高；断面ZK0＋290的线性相关系数R＝0.722 1，其值介于0.3～0.8之间，故该工程区间段可用Peck公式进行沉降预测。

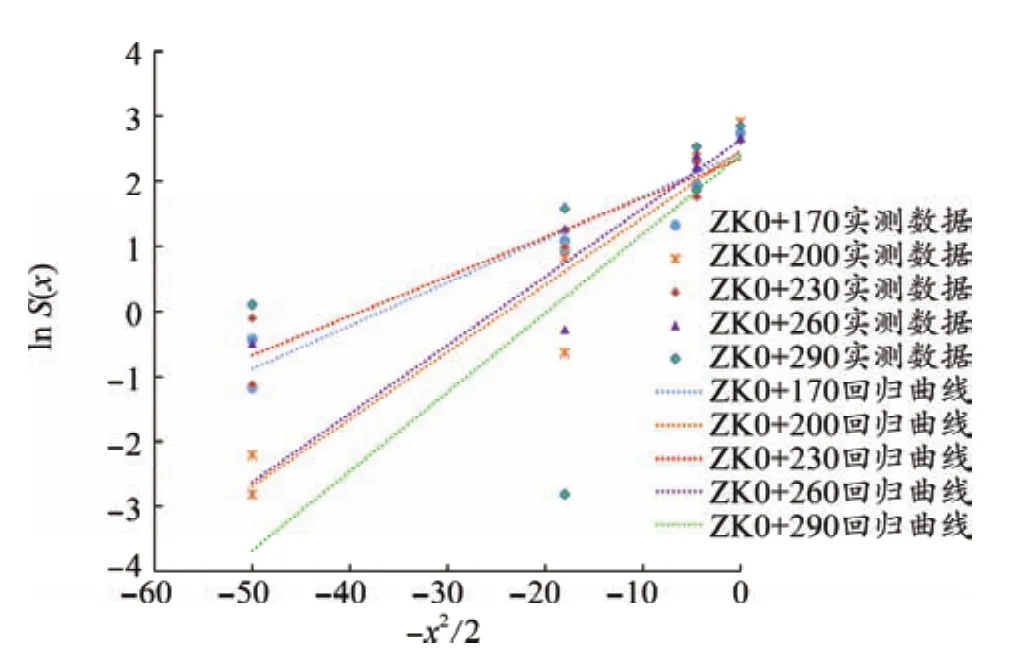
图4 各监测断面回归情况

将求得参数代入式（1）可得到线性回归后的Peck公式：

由回归分析后所得Peck公式，可得出地表预测最大沉降量Smax和沉降槽宽度系数i，如表3所示，并将实测值与Peck公式预测曲线进行对比分析，如图5所示。

表3 沉降槽宽度系数和地表最大沉降量拟合值

图5 各断面实测值与Peck预测曲线

本地区各断面土层参数较为接近，隧道埋深及施工参数也较为接近，但各断面之间先后掘进顺序不同，水文地质条件及覆土厚度也各有不同，故各断面监测数据不尽相同。根据线性回归分析得到的Peck公式进行数据分析可知：除断面ZK0＋290外，断面ZK0＋170、ZK0＋200、ZK0＋230和ZK0＋260都具有较高的拟合度，其线性相关系数均大于0.8，且5个断面的线性回归相关性系数均高于0.7，符合Peck公式在该地区的运用条件。由图5和表2可知，地表沉降工程测量值与Peck曲线拟合值较为相近。因此，基于Peck公式运用最小二乘法进行拟合得到的回归函数，能够对该地区盾构施工时引起的地表沉降进行很好地预测。

由表3可知：对于该地区典型砂性土层条件，地表最大沉降值Smax取值范围为10～14 mm；地表沉降槽宽度系数i取值范围为2～5。

4．2 纵向地表沉降分析

根据工程实测数据绘制断面ZK0＋200、ZK0＋230和ZK0＋260三个断面的点位沉降－时间曲线，并进行分析，如图6～图8所示。

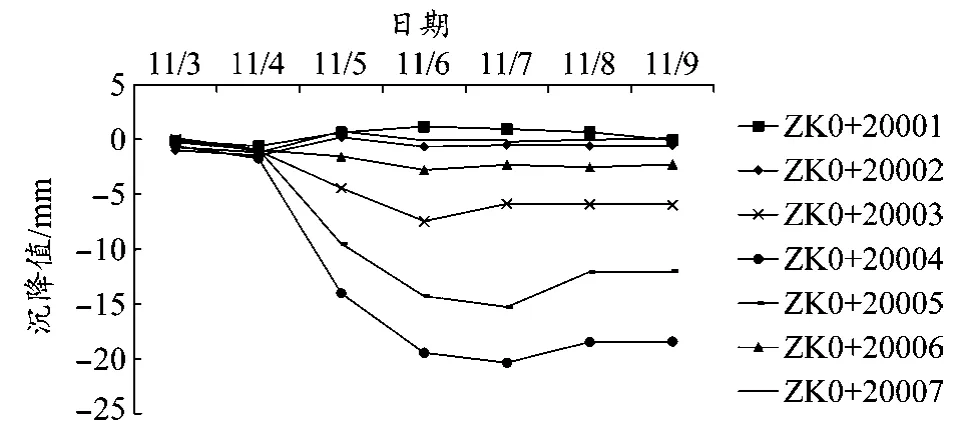
图6 ZK0＋200监测点沉降－时间关系曲线

图7 ZK0＋230监测点沉降－时间关系曲线

图8 ZK0＋260监测点沉降－时间关系曲线

由图7可知，当开挖至ZK0＋230断面时，在ZK0＋230断面后方10 m、20 m的中线点发生2～3 mm的沉降，且距断面20 m处较大；除此之外，在ZK0＋230监测断面前方10 m、20 m处发生0～1 mm隆起，且距断面10 m处隆起值较大。随着盾构施工的进行，当盾构衬砌脱离盾尾时，ZK0＋230监测断面后方同样位置处，沉降量急剧增大到12～18 mm，且单次最大沉降值为总沉降值的0.7～0.8倍。注浆处理后，地表沉降逐渐趋于稳定状态，土层也随之发生蠕变和固结现象，且在1～4 mm范围内；随着开挖继续进行，ZK0＋230监测断面各监测点沉降值急剧增大，其中ZK0＋23004监测点沉降值为12 mm，为该点总沉降值的0.85倍，其沉降速率先趋于缓慢，然后逐渐达到平稳状态。该断面的其他测点变化规律与之相似。

ZK0＋200和ZK0＋260断面各监测点沉降规律与ZK0＋230断面大致相同。ZK0＋200断面最大单次沉降为12.28 mm，为该处总沉降值的0.66倍。与其他两个断面相比，其单次沉降占比较小。此现象表明该断面各点的沉降速率比其他两个断面各点的沉降速率较小，可能是由于盾构机掘进速度的变化与上覆土层厚度不同所造成。通过对大量工程监测数据的分析，发现工程地质条件相近、施工条件大致相同时，盾构施工对地表沉降的影响会随着上覆土层厚度的增大而减小，但施工影响范围会变大。

由现场工程资料可知，断面ZK0＋230上覆土层厚度比断面ZK0＋200上覆土层厚度大1 m，ZK0＋230断面较ZK0＋200断面中线监测点沉降最大累计值小4.63 mm，ZK0＋230断面较ZK0＋200断面距隧道边缘3 m处监测点沉降累计值大1～2 mm。此现象的产生，是由于隧道开挖时，在垂直方向距地表较远，因土体损失向水平方向发展，致使垂直方向土体损失逐渐减弱。

5 结论

本文基于某市城市地下综合管廊项目D1-D2区间的现场监测数据，运用最小二乘法最优化方法对Peck公式进行拟合。通过拟合Peck曲线得到适用于该地层沉降槽宽度系数i初步取值范围为2～5；地表最大沉降值Smax取值范围为10～14 mm。对3个监测断面监测点进行纵向地表沉降分析得知，盾构施工时，在距盾构机前后15～20 m范围内，土体会产生隆起和沉降现象；当盾构机脱离洞口时，盾尾脱出部位沉降速率最大，其沉降量占总沉降量的70%～80%。研究成果对该地区同类型工程的设计和施工具有一定的参考价值。