考虑复合滑动边坡内部剪切约束机制的 刚体极限平衡方法

衣天宇，卢 波，邬爱清，徐栋栋，王 瑾

(长江科学院 水利部岩土力学与工程重点实验室，武汉 430010)

1 研究背景

在世界水利史上，许多滑坡事件的发生在工程界和学术界具有里程碑式的意义。自1964年Mǜller-Salzburg[1]发表第一篇关于Vajont滑坡的文章以来，对于滑坡破坏机理的研究一直持续至今。Vajont滑坡已成为目前研究最多、发表文献最多的案例。总体来看，研究主要覆盖了滑坡的地质条件[2-4]、成因机制[5-7]、监测成果分析[8]、滑面力学参数测试与反分析[9-11]、滑坡灾害过程模拟[12-13]及工程运行处置决策的反思[14-15]等各个方面。众多研究者把滑坡的成因归结为多种因素引发了巨型顺层状岩体滑坡，包括滑坡前缘河谷深切、卸荷裂隙发育、岩体顺倾且存在软弱黏土夹层成为主要滑动面、前期连续降雨、水库水位未能及时降低和斜坡内地下水位升高和孔隙水压力增大等。虽然对于Vajont滑坡高速滑动的原因及灾害本身能否避免等关键问题未能取得完全一致的认识，但诸多研究成果全面深化了对该滑坡的地质条件、滑面的力学参数取值、滑坡变形发展演化过程等方面的认识。

值得注意的是，综合各研究成果来看，Vajont滑坡滑面的摩擦角介于10°～12°[10-11]，然而根据Mǜller等利用极限平衡进行的反分析计算结果，滑面摩擦角应该在18°～28°之间，而10°～12°的摩擦角不足以维持滑坡整体稳定性[9]。针对这一问题，许多学者从不同角度给出了解释。Mencl[16]假设滑动面的转折部分形成了空腔或间隙，使岩石在塑性流动的过程中转变为机械运动；Yerro等[17]改进了Vajont滑坡计算的本构模型，通过物质点法(MPM)进行数值模拟计算，验证了滑坡内部的剪切变形机制；Alonso等[18]在解析解模型中考虑了内部剪切变形机制，但他假设剪切破裂面位于滑面的角平分线，显然不符合实际情况。

本文以简化的Vajont滑坡模型为研究对象，从传统极限平衡方法入手提出研究存在的问题，通过假定剪切破裂面的位置，推导了考虑复合滑动边坡内部剪切约束机制的刚体极限平衡方法即三滑面分析法。在三滑面分析法的基础上可计算最小安全系数与滑体内部剪切破裂面具体位置，并通过参数敏感性分析研究了滑坡抗剪阻力的弱化对滑坡整体稳定性的影响机制。

2 刚体极限平衡分析及存在的问题

2.1 计算模型建立

根据Hendron和Patton[11]于1987年绘制的Vajont滑坡典型剖面(图1[11]，P1、P2为钻孔)，建立了用于刚体极限平衡的简化模型。模型由下部基岩和基岩上的滑坡体组成，潜在滑动面位于基岩与滑坡体之间(图2)。

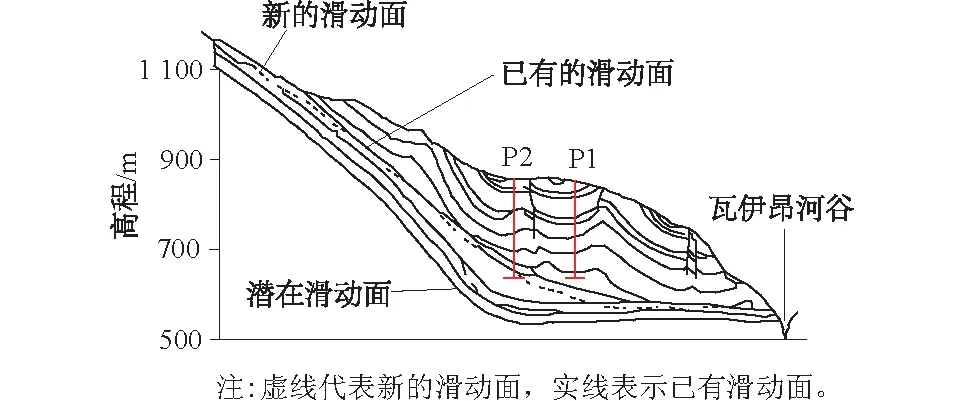
图1 Vajont滑坡典型剖面[11]Fig.1 Typical section of the Vajont landslide[11]

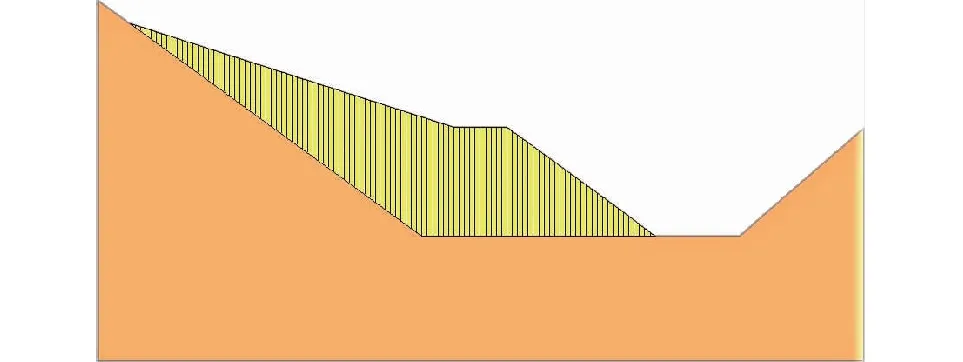
图2 Vajont滑坡极限平衡法计算条分图Fig.2 Slice graph of limit equilibrium method for Vajont landslide

关于Vajont滑坡参数取值的研究有很多，在众多学者的研究基础上[19-21]，结合工程岩体分级标准，采取经验法给定滑坡体和基岩的计算参数，如表1所示。

表1 滑坡强度参数取值 Table 1 Strength parameters of landslide

2.2 计算结果分析

摩根斯坦-普莱斯法(M-P法)是刚体极限平衡法中最严格的方法，适用于求解任意形状滑裂面的安全系数。采用M-P法，分别选取滑面摩擦角φ=10°～28°进行计算，黏聚力取值均为0 MPa，得到的滑坡安全系数计算结果如图3所示。

图3 M-P法计算结果Fig.3 Calculation result of M-P method

由图3可知，当摩擦角取15°～16°之间时，滑坡整体安全系数为1。这一结果与Mǜller-Salzburg[9]的极限平衡反分析结论相吻合。

2.3 存在的问题

对于复合滑面滑坡而言，潜在滑面转折部位处会有滑移方向的改变。为了适应改变，斜坡体内部将在转折部位发生剪切错动。以Vajont滑坡简化模型及滑动过程为例，如图4、图5所示(图中虚线表示滑坡体初始形状，实线表示滑坡体变形过程)。上部主动滑块初始的整体滑移方向沿上部滑移面向下为v1，下部被动阻滑块滑移方向为v2。在破坏过程中，当上部主滑块前缘部分首先越过滑移面转折处，即将成为阻滑块一部分时，滑移方向由v1突变至v2，由此导致这部分块体在v12方向产生剪切错动。坡体变形对滑坡沿潜在复合滑面的剪切滑移形成了一定的约束，这种剪切变形机制就是复合滑坡的破坏机制和约束机制。

图4 主滑块-阻滑块简化模型Fig.4 Simplified model of slide

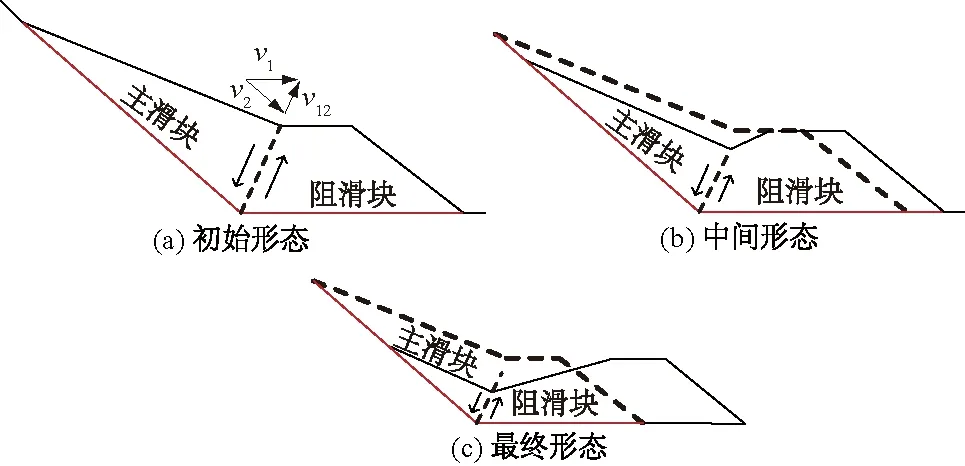
图5 滑移过程中主滑块-阻滑块两块体的转化示意图Fig.5 Transformation between major sliding bock and sliding-resistant block in the process of sliding

根据上述分析，由于传统的刚体极限平衡法并未考虑滑坡体内部的剪切变形机制问题，所以剪切约束对滑坡体整体稳定性的贡献未能得到体现。为了进一步分析Vajont滑坡的约束变形机制，探究滑坡内部剪切面的形成过程对滑坡整体稳定性的影响，在考虑滑面极限平衡分析的基础上进一步考虑滑体内部剪切破裂面上的力学平衡，建立平衡方程进行联立求解。

3 考虑内部剪切约束机制的刚体极限平衡方法(三滑面分析法)

3.1 基本思想和计算模型

考虑内部剪切约束机制的刚体极限平衡方法的关键在于确定内部剪切破裂面的位置，这里建立的简化计算模型如图6所示。

图6 三滑面计算模型Fig.6 Calculation model of three slip surface

(1)滑坡体的初始构型为一多边形OABCDE，记后缘滑面倾角为α，前缘滑体高度为h，后缘滑面长度、后缘块体内部夹角为γ，前缘滑面长度以及CD的长度分别为L1、L2、L4，滑坡体后缘滑面与前缘滑面的夹角为∠OAB；记内部剪切面AE与后缘滑面的夹角为β，这里β是待求未知变量；记AE的长度为L3。

(2)滑体内部剪切面AE上存在抗力Q，记抗力与水平方向的夹角为变量φ，抗力Q在AE面存在水平和垂直向的分量；Q和φ都是求解过程中需要确定的未知变量。

(3)OA、AB以及AE三个面上的安全系数为各面抗滑力与下滑力的比值。

通过在后缘滑面、前缘滑面和内部剪切破裂面上分别建立极限平衡方程，进行联立求解，获得β角(即确定AE的位置)和滑坡体整体性安全系数。

3.2 第一、第二滑面安全系数

后缘块体受力如图7所示。设OA面(第一滑面)上的摩擦角、黏聚力分别为φ0、C0，OA滑面上的力的安全系数为

图7 后缘块体受力示意图Fig.7 Schematic diagram of forces acting on the rear edge block

(1)

式中：W1为后缘块体的重力，W1=m1g，m1为后缘块体的质量，g为重力加速度。T1为OA面上的抗力，即

T1=C0L1+N1tanφ0。

(2)

式中N1为岩体对滑面OA的反作用力，根据平行于OA面的平衡方程，可以计算得到

N1=Qsin(α-φ)+W1cosα。

(3)

前缘块体受力如图8所示。假设AB滑面(第二滑面)与OA滑面(第一滑面)抗剪强度参数一致，滑面长度为L2。AB滑面上的安全系数为

图8 前缘块体受力示意图Fig.8 Schematic diagram of forces acting on the leading block

(4)

其中:

T2=C0L2+N2tanφ0;

(5)

N2=Qsinφ+W2。

(6)

式中：W2为前缘块体的重力;m2为前缘块体的质量；T2、N2为AB面上抗力。

3.3 第三滑面安全系数

AE(第三滑面)为位置待定的剪切破裂面，抗剪参数为φ1、C1，AE面上的作用力只有抗力Q，Q与AE面的夹角为(α+β-φ)。AE面上的安全系数为

(7)

根据模型的几何关系，L5为AD边长度，θ为AD与AB的夹角，γ为OA、OE夹角，δr为岩石密度。则有:

(8)

(9)

(10)

3.4 求解方法及结果

根据上述力学平衡方程推导结果，3个滑面的安全系数分别为式(1)、式(4)、式(7)。未知数共4个，即Q、β、φ、F。计算时先假定一个β角，在给定β角度下求解联立方程组，寻找整体安全系数最小的解。β取值存在一定范围，在理论上>0°，小于∠OAB。可以预见，β较小时，后缘主动块的体量小，下滑力小，不足以推动下方的被动块；但若β太大，则对下方的被动块提供下滑力的同时，也贡献了阻滑力(对被动块存在竖直向下的分量)。因此在β取值范围内，一定存在特定的角度值对应得到最小的安全系数。这里的计算参数与第2节中M-P法一致(滑面摩擦角φ=10°，C=0 MPa；滑坡体摩擦角φ=33°，C=0.1 MPa)，结果见表2。

表2 三滑面法计算结果Table 2 Result of safety factor calculated by the three-slip-surface method

从表2可以看出，抗力Q的作用方向随β角的改变有较大变化，在-8.31°～56.95°之间，而(α+β-φ)即抗力与剪切面AE的夹角变化不大，在54.31°～47.38°之间。在相同的强度参数下进行计算，三滑面分析法的计算结果表明，当β=50°～60°时安全系数最小，最小值为0.76；而M-P法计算安全系数较小，为0.63。取滑面摩擦角在10°～12°的范围内进行计算，三滑面分析法的结果在0.7～0.9，始终大于M-P法的计算结果。该结果表明，滑坡的内部剪切阻碍对滑坡整体稳定存在一定的约束机制。

3.5 滑体内部剪切约束机制讨论

研究[22]表明，在水库初次蓄水时Vajont滑坡体发生过形变，降低水位后变形得到了控制，最后一次蓄水达到650 m时，滑坡变形在瞬间完成。目前，越来越多的学者认为，水库蓄水导致强度参数弱化是Vajont滑坡的诱发因素。强度参数的弱化必然会降低整体的安全系数，但参数弱化条件下剪切面角度与安全系数关系的变化缺乏研究。滑面与滑坡体强度参数的弱化都会对滑坡整体稳定产生影响，下面分别讨论2种情况下的结果。

(1)保持第一和第二滑面的强度参数取值不变，对第三滑面抗剪强度参数C、φ值分别进行敏感性分析，计算结果如图9所示。

图9 剪切面参数敏感性分析结果Fig.9 Sensitivity analysis of shear plane parameters

摩擦角和黏聚力的降低，都会使滑坡整体的安全系数降低，但摩擦角的影响作用更加明显。这是由于三滑面分析法假定剪切面上抗力的计算符合摩尔-库伦准则，即T=Qsin(α+β-φ)tanφ1+C1L3，T为剪切面上的抗力。根据计算参数取值含有摩擦角一项的值要远大于黏聚力一项的值，所以摩擦角的数值变化对抗力大小的影响更大。随着摩擦角取值的减小，滑坡安全系数达到最小时的剪切面角度略微增大。在φ=30°时，剪切面与第一滑面的夹角为50°左右时，安全系数最小；当φ=27°时，剪切面角度取值增大至60°左右。

由此可见，滑坡岩土体自身的强度参数越高，即抵抗剪切破坏的能力越强，则对滑体整体性的贡献则越大。

(2)保持第三滑面的强度参数取值不变，将第一和第二滑面的强度参数φ值进行敏感性分析，计算结果如图10所示。

图10 滑动面参数敏感性分析结果Fig.10 Sensitivity analysis of sliding surface parameters

滑面摩擦角对滑坡安全系数的影响更加明显，随着摩擦角的减小，安全系数迅速降低。不同摩擦角的取值下，最小安全系数对应的剪切面角度无明显变化。

4 结论与展望

(1)对于复合滑面滑坡而言，潜在滑面转折部位处会有滑移方向的改变。为了适应改变，斜坡体内部在转折部位发生剪切错动。坡体的变形对滑坡沿潜在复合滑面的剪切滑移形成了一定的约束，这种剪切变形机制可能会构成复合滑坡的破坏机制，对滑坡的整体失稳破坏产生一定约束。

(2)建立了考虑滑坡内部剪切约束机制的三滑面极限平衡分析方法。以Vajont滑坡为例进行了分析。研究表明，随着剪切面角度的增大，滑坡安全系数逐渐减小。当剪切面角度达到50°～60°时，F=0.76，为最小值。取滑面摩擦角为10°～12°进行计算，最小安全系数始终大于M-P法的结果，因此滑坡的内部剪切阻碍对滑坡整体稳定存在一定的约束机制，剪切面的存在有可能使滑坡在较小的摩擦角下依然维持整体稳定。

(3)对滑体内部剪切破裂面的C、φ值进行了敏感性分析， 结果表明滑坡岩土体自身的强度参数越高，即抵抗剪切破坏的能力越强，对滑体整体性的贡献越大。

(4)从运动学角度进行理论分析，可以证明剪切面的合理性，但缺少数值模拟的结果进行直观的验证。可以考虑运用非连续变形分析(DDA)的方法，解决这一问题。对于非连续变形分析方法国内外有许多研究，其在模拟大变形、非连续问题上有明显的优势。