富水区隧道围岩多场参数反分析研究

寇海军

（中铁十九局集团第五工程有限公司 辽宁大连 116100）

1 引言

软岩及高地应力水平下的中等强度岩体或节理发育的硬岩工程都存在蠕变效应，随着地下工程向深部发展，常会遇到应力、渗流以及温度耦合影响的蠕变问题。关于温度、应力、渗流等耦合作用下岩体蠕变特性及其本构模型已开展了大量的研究工作。

黄书岭等[1]、刘建等[2]通过试验研究了耦合条件下岩石的蠕变与渗流、应力之间的关系。从数值模拟及本构模型的角度，郤保平等[3]、王永岩等[4]、MA L J等[5]研究了温度场、应力场、化学场耦合条件下岩体的蠕变规律。无论是理论分析还是数值模拟均离不开岩体参数，其在工程设计与施工中起着至关重要的作用，参数反分析方法作为一种确定参数的有效手段，受到广泛关注[6－7]。在蠕变参数反演方面，陈静等[8]、徐国文等[9]提出相关反演方法，并在工程实际中进行应用。目前大多数研究针对单场参数反演，而对多场耦合下参数反演研究较少。贾善坡等[10]提出泥岩渗流－应力耦合蠕变损伤模型，采用优化反分析法得出蠕变损伤模型中的待定参数。刘开云等[11]将高斯过程回归（Gaussian Process Regression，GPR）引入隧道工程进行模型参数反演，并采用单一各向同性核函数之和作为GPR的组合核函数以提高其泛化性能。孙钱程等[12]在改进多输出支持向量机算法（MSVM）的基础上，建立基于贝叶斯理论的概率反分析方法（B-MSVM方法）。

本文针对多场耦合下岩体蠕变参数较难获得的问题开展反分析研究，基于免疫算法和BP神经网络的应力－渗流耦合作用下隧道围岩蠕变多参数反演方法进行。以兰州至海口国家高速公路（G75）某石质特长隧道为工程实例，基于现场监测数据进行应力－渗流耦合条件下隧道围岩蠕变多参数反演。

2 应力－渗流耦合蠕变模型

高地应力软岩隧道围岩具有明显蠕变性，一般而言，将存在蠕变行为的总应变分解为弹性应变、塑性应变、蠕变应变，即：

式中：ε为总应变；εe为弹性应变；εp为塑性应变；εc为蠕变应变。

可依据需求在ABAQUS软件中自行选择蠕变定律，该软件具有Singh-Mitchell、应变硬化及时间硬化三大蠕变定律可供选择。

（1）时间硬化蠕变定律

（2）应变硬化蠕变定律

（3）Singh-Mitchell蠕变定律

本文考虑蠕变非线性，采用时间硬化蠕变定律，岩石的总蠕变可以表示为

式中：εt为瞬态蠕变；εs为稳态蠕变。

对于瞬态蠕变和稳态蠕变可以采用幂次法则模式来描述：

式中：σ为等效应力；n为应力指数；A为蠕变系数；t为时间；m为时间指数。

本文取m＝0，则式（6）简化为：

3 IA-BP多参数反演方法与实施

免疫算法能够在寻求全局最优解过程中，对多峰值函数寻优出现的 “早熟”问题进行妥善处理。利用免疫算法优化BP神经网络的权值与阀值，并建立IA-BP智能反分析方法，进行应力－渗流耦合隧道围岩蠕变多参数反演。

采用ABAQUS软件对基于正交试验设计方法构造样本，并对样本参数进行计算作为IA-BP算法的样本值。

在进行IA-BP算法参数反演前，对BP神经网络隐含层和输入层的参数进行设置，并对BP神经网络结构参数进行初始化。

其次，对免疫算法的种群数、免疫基因数量等参数进行设置，其中BP神经网络权重之和用基因个数D来表示。其隐含层、输出层、输入层神经元数量用S1、S2和R来代表，则粒子群维数公式：

计算抗原抗体的亲和度，亲和度函数：

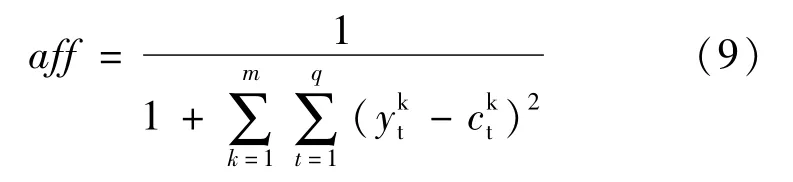
将神经网络的输入向量设定为围岩位移量，输出向量设定为隧道围岩岩体参数，对隧道围岩位移与围岩参数之间的非线性关系建立关系函数。优化目标函数为：

式中：x为待反演参数；fi（x）为第i个量测方向的计算位移值；ui为第i个计算向量的实际位移；n为隧道围岩位移监测点数量。

按照隧道实际尺寸进行数值建模，边界影响条件考虑3倍洞径，故几何模型尺寸为横向X轴50 m，纵向Y轴长度50 m，模型拱顶至上部边界19.5 m，模型拱底至底部边界22.5 m，如图1所示。

图1 有限元模型

隧道围岩参数范围如表1所示。本次数值计算共选择6个试验主控参数，对每个主控试验参数选取5个水平因素，基于正交设计方法，选择 L25（56）正交试验表进行方案设计，正交试验方案如表2所示。对正交试验方案中的每组试验参数进行对应的数值计算，借助ABAQUS软件计算正交参数组下的围岩位移值。

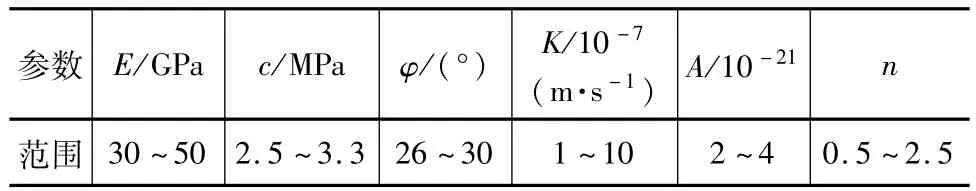
表1 岩体参数

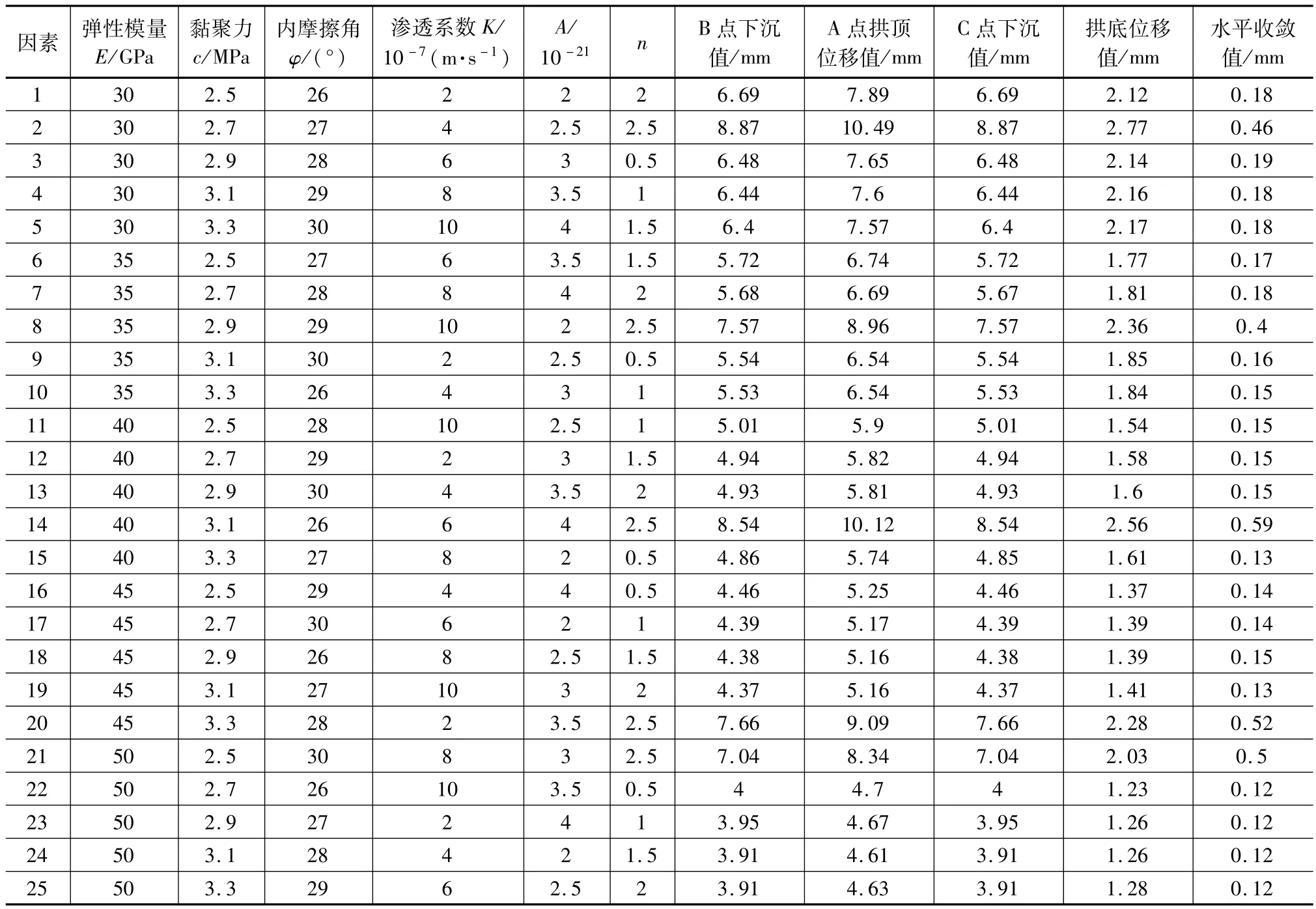
表2 正交设计

通过MATLAB软件，借助IA-BP智能算法，对表2正交设计试验组中的围岩参数与围岩位移值建立非线性关系，通过反演得到IA-BP的学习样本值。IA-BP智能算法学习值与计算试验值数据对比如表3所示。

表3 试验值与IA-BP算法对比

对试验值与IA-BP算法值进行残差值计算，计算结果如图2所示。由图2可知，除了渗透系数偏差较大外，其他各参数大多数点都在零附近。由表3与图2可知，计算试验值和反演值之间误差较小，说明该算法对隧道应力－渗流耦合多参数反演具有较高的计算精度。

图2 残差值计算结果

将反演参数代入ABAQUS进行模拟可得到围岩与支护结构的应力、位移以及塑性区分布。隧道完成开挖90 d后，及随开挖步隧道围岩位移变化云图如图3所示。当隧道完成第一、第二开挖步时，隧道拱顶围岩发生较大位移变化；当完成第三步开挖及开挖完成后第90天的隧道围岩位移变化较为平稳，此时隧道围岩趋于稳定状态。

图3 隧道围岩竖向位移变化云图

4 工程应用

4．1 工程概况

渭武高速公路土建第十七合同段起讫里程K345＋800～K350＋000，线路为分离式通行，双线折合全长为8.4 km。某隧道为渭武高速陇南段特长隧道，为左、右双洞分离式设计，左线工程段长度为3 009 m，渭武十七标承建出口端2 243 m；右线全长为3 209 m，渭武十七标承建出口端2 460 m。

4．2 基于现场监测数据的参数反演

该工程YK345＋907位置，隧道上断面开挖后拱顶发生沉降、边墙周边收敛，在套拱前沉降达80 mm，周边收敛达154 mm，收敛值为沉降值的1.925倍。施作套拱后拱顶沉降及周边收敛速度明显降低。下台阶开挖后围岩被进一步扰动，拱顶沉降及周边收敛发生突变，仰拱封闭后拱顶沉降及周边收敛趋于稳定，最终拱顶沉降稳定于129 mm，周边收敛稳定于263 mm。对数据进行分析发现，采用上下台阶法进行隧道开挖时，隧道围岩水平收敛及拱顶沉降值之间差异较大，拱顶沉降值为94 mm，水平收敛值高达219 mm，在拱顶沉降最大值与水平收敛最大值中占比分别为72.3%及83.2%。其中，开挖过程引起的仰拱及下台阶沉降为36 mm，水平收敛值为44 mm，分别占最终沉降和收敛的27.7%和16.8%。

选取对数型及指数型函数对隧道位移数据进行回归处理，拟合结果较为理想。沉降测点C1及收敛测线S1回归结果如图4、图5所示。

图4 隧道拱顶沉降拟合曲线

图5 隧道收敛拟合曲线

基于监测数据，采用反分析方法进行参数反演，参数反演结果如表4所示。

表4 参数反分析结果

4．3 现场隧道突水与支护方案

隧道出口端右线掌子面施工至YK347＋792处，正在进行出渣作业时，线路左侧上台阶拱脚以上1.5 m位置突然出现多处高压股状涌水，如图6所示。出水量经初步测算约430 m3／h，2 h之后突水量基本稳定，经测算约260 m3／h，隧道涌水至二衬地段。突水水质浑浊，呈火山灰红色，水流中伴有碎石、泥土等。突水发生之后，YK347＋807～YK347＋792段初期支护大面积涌水，发生多处环向、纵向开裂。

图6 隧道掌子面突涌水

出水量稳定后及时对该段初期支护断面进行沉降收敛监控量测，YK347＋798.852断面顺里程前进方向左侧侵限30 cm，下沉11.7 cm；YK347＋804断面顺里程前进方向左侧侵限7 cm，右侧侵限3.6 cm，下沉5.4 cm。

通过参数反演对隧道稳定性进行分析，初期支护施作钢拱架临时仰拱，径向设置三道工字钢斜撑，如图7所示。对各断面进行 2次／d的加密监测，经数据分析于2017年1月15日沉降、收敛值基本趋于稳定。

图7 隧道右线涌水后初期支护施作临时仰拱及斜撑

5 结论

以兰州至海口国家高速公路（G75）某隧道为工程实例，基于现场监测数据，采用建立的IA-BP算法进行应力－渗流耦合下隧道围岩多参数反演，拓展了参数反演应用范围。AI-BP算法对于多参数反演的精度较高，体现出其全局搜索最优解的特点，证明基于AI-BP算法的反分析方法是一种高效的多参数反演方法，可以用于应力－渗流耦合复杂环境下的隧道围岩蠕变多参数反演。基于监测数据反演应力－渗流耦合下隧道围岩蠕变多参数，各测点位移值与实测值基本吻合，即反分析得出的参数值为能够反映隧道变形规律的“真实值”。根据反演参数进行隧道稳定性分析，实现了复杂环境下反分析与位移信息反馈动态设计相结合，为工程施工提供依据。