浓缩机耙臂的扭矩试验机及剪切模型研究①

赵 睿，石云良，肖金雄，柯佳焱

（长沙矿冶研究院有限责任公司，湖南 长沙 410012）

浓缩机（浓密机）是选矿厂常用的精矿、尾矿脱水设备之一，其脱水原理是利用重力沉降将悬浮液中的固体颗粒分离出来以实现固液分离［1－4］。

浓缩机的扭矩设计值是影响浓缩机能否长期稳定、高效运行的关键性因素，浓缩机系统所承受的扭矩来源于耙架在转动时克服浆料的屈服应力和运行过程中对矿浆剪切过程中产生的剪切应力［5］。如果浓缩机的设计扭矩过低，在实际运行过程中容易产生鼠洞、过载停机甚至压耙现象，而压耙有可能损坏浓缩机驱动部分、中心柱及耙架钢结构，一旦其中任何部分受损，就必须停机维修，致使整个生产系统被迫停车，对矿山企业的效益产生严重影响［6］。

在浓缩机的扭矩设计中，耙臂所受的扭矩同刮板一样不能被忽视。随着我国在节能环保方面的要求越来越高，在浓缩机驱动扭矩设计时必须满足矿山实际需求，同时又兼顾经济环保要求，合理把握浓缩机扭矩设计才能有效地避免生产资源和能源的耗费［7］。

本文设计制造了一套可以实测耙臂扭矩值的小型浓缩机，通过浓度、耙臂转速等因素对扭矩的影响试验，进行工业浓缩机的条件模拟试验，研究浓缩机耙臂在耙架运动区受力情况，形成一套浓缩机耙臂扭矩计算模型及相应方法，可为工业大规模浓缩机的耙臂扭矩设计提供一定数据支持。

1 试验设计

1.1 试验物料

试验所用物料取自国内某辉锑矿选矿厂浮选全粒级尾矿，矿样粒度组成见表1。由表1可见，细粒级物料尤其是－20μm粒级占比较高，属较难沉降类尾矿。

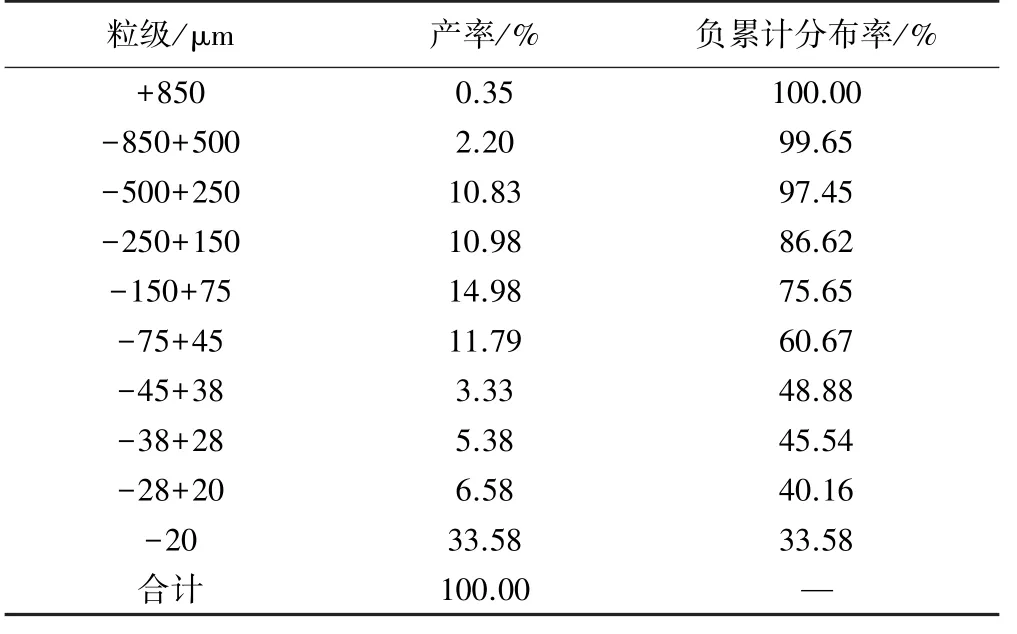
表1 试验物料粒级组成

用比重瓶法测量该矿石样品真密度3次后取平均值，求得其真密度为2.65 g／cm3。采用流变仪检测分析试验样品，通过流变曲线可知该物料在浓度60%以上时具有典型的非牛顿体特征。

1.2 实验室小型试验浓缩机系统的设计

本文研究设计的模型系统如图1所示。试验机主体分为驱动、测量组件与筒体组件，驱动、测量组件由“门”形支架支撑，由上方的减速电机来驱动下方的浓密机主轴部件，减速电机与主轴之间通过联轴器连接动态扭矩传感器，传感器可直接采集主轴承受的驱动扭矩数据。主轴下方设计有两根对称耙臂，驱动电机工作电压由直流电源控制，根据输入电压不同可提供多种驱动速度。浓缩机筒体部分采用分体式法兰连接，高径比可变，也可以替换不同锥角的池底组件。试验样品添加至搅拌给料器后被给料泵泵入浓缩机中，底流通过底流输送泵送回搅拌器，完成物料的给排料循环。

图1 扭矩试验装置主体视图

1）高灵敏度扭矩测量仪器仪表的选型与设计安装。传感器采用DYN－200型动态扭矩传感器，扭矩测量范围为0～3 N·m，误差不高于0.03%，采样速度40次／s。扭矩传感器可将测量数据通过模拟信号传输至电脑端，使用专业采集软件分析处理。传感器通过联轴器与上方微型直流电机及下方耙架主轴相连，主轴转动部位使用轴承以降低转动阻力。

2）驱动单元选型。驱动单元设计为型号P50的减速电机，额定电压24 V，额定扭矩不低于36 N·m，减速比3 496.71。驱动电压与转速为线性关系，根据转速随电压值的变化进行线性拟合，关系式为：

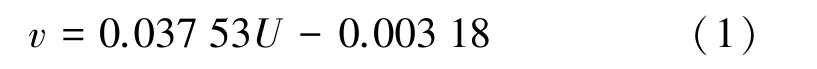
式中v为耙架转速，r／min；U为供电电压，V。式（1）的相关系数为0.999 8。

1.3 试验方法

将配制好的固定浓度的样品搅拌均匀后通过胶管泵均匀添加至浓缩机内部，到达设定的泥层高度后将浓缩机底部排矿管与胶管泵进料管相连接，完成试验浓缩机的给、排料循环，在此基础上进行不同条件下的驱动扭矩数据采集试验，试验流程如图2所示。根据目前膏体浓密机底流浓度大部分高于60%的情况，确定物料给料浓度应不小于60%。浓度高于60%的矿浆具备较好的均匀混合性质，加上试验为动态循环，每次试验结束后均会抽出位于浓缩机底部矿浆，测量其浓度并与给料浓度进行比对，未见明显沉降情况发生，因此判断在试验过程中不会发生沉降离析现象。每次在给料稳定循环20 min后开始扭矩数据采集。

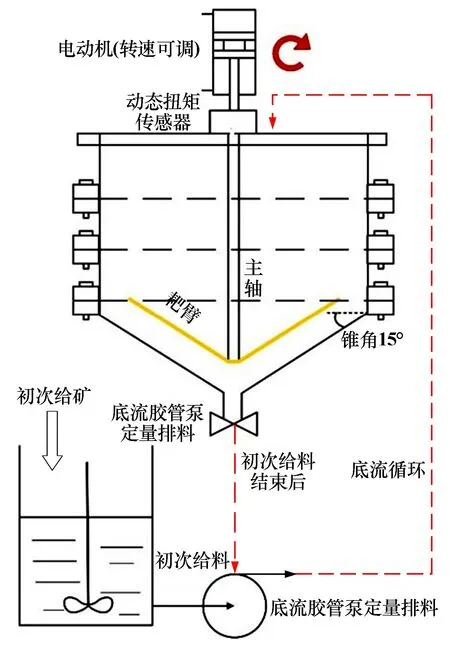
图2 试验流程示意图

2 试验结果

扭矩试验结果如表2所示。

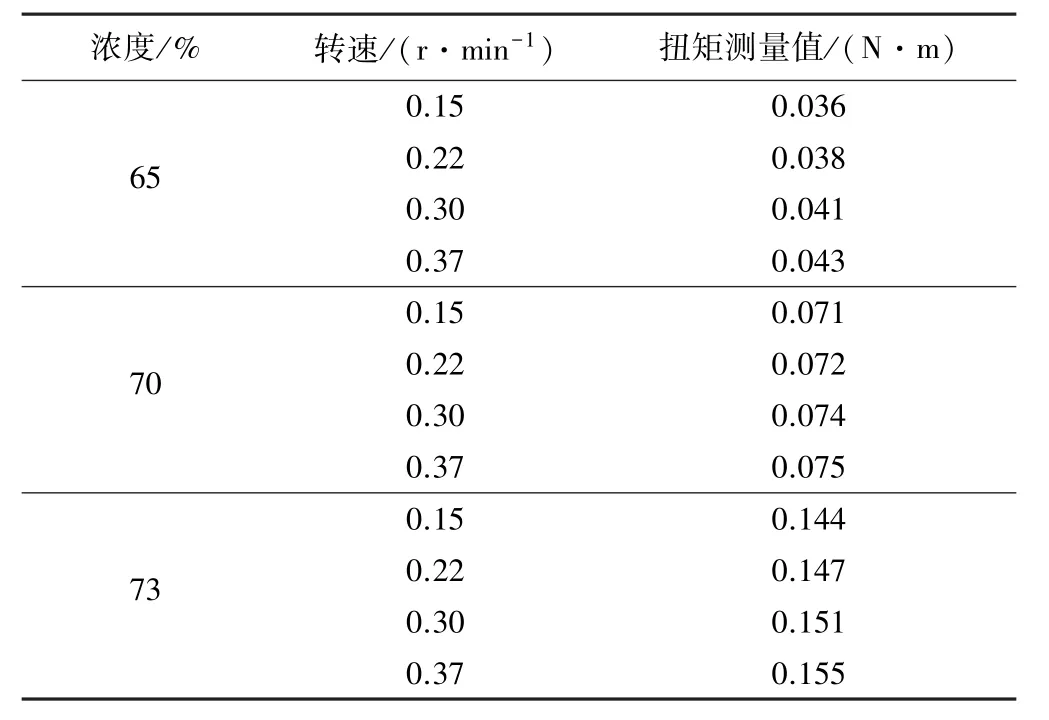
表2 试验实测扭矩结果

3 扭矩数学模型的建立

3.1 屈服应力与浓度关系的回归拟合

采用Anton Paar MCR72型旋转黏度计对不同浓度的尾矿样品进行剪切速率及剪切应力检测，剪切测试中，采用极低的剪切速率（0.3 s－1）对浆料进行缓慢剪切作用，测试得出的最大值视为当前浓度浆料的屈服应力。不同浓度尾矿样品的屈服应力检测值如表3所示。由表3可知，随着样品浓度升高，对应的屈服应力值随之上升，总体呈指数关系。

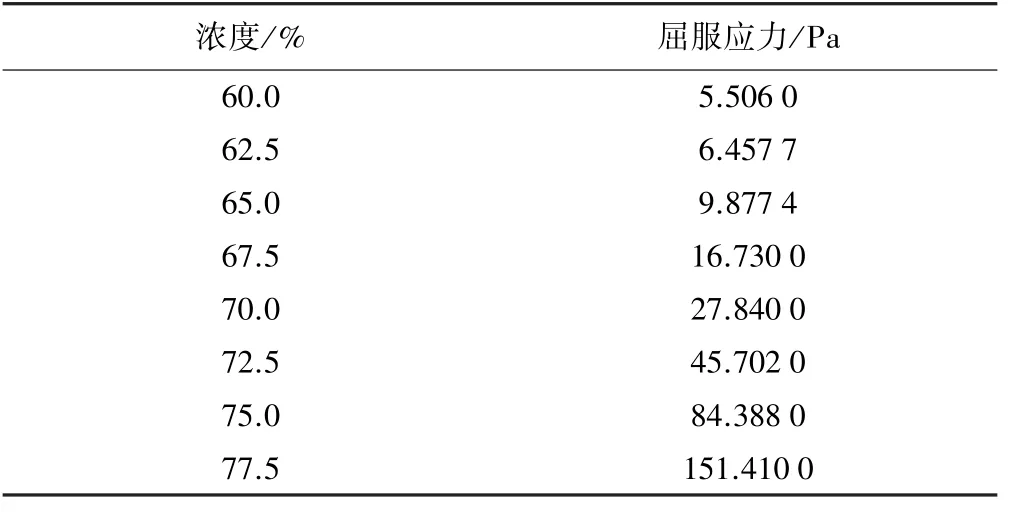
表3 物料浓度与屈服应力对照关系

对表3数据进行非线性拟合，通过回归分析可知，浆料屈服应力随矿浆浓度的变化遵循ExpDec1函数，相关系数R2＝0.999 8：

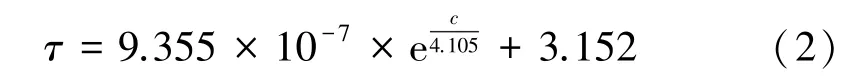
式中τ为浆体屈服应力，Pa；c为浆体质量浓度，%。

3.2 耙臂受力分析及扭矩数学模型的建立

根据力学公式，扭矩可用屈服应力及剪切面积表示：

式中T为剪切扭矩；τ0为剪切发生时物料的屈服应力，Pa；A为剪切过程中的剪切面积，m2；r为力臂长度，m。

通过试验观察发现，耙臂在运动期间会推动前方的一部分矿浆，这部分被推动的矿浆具有规律性的形态，实际形态边缘部分为圆弧形，如图3所示。

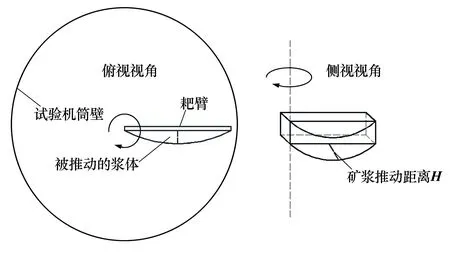
图3 试验机耙臂实际剪切模型示意图

为了模型计算的方便，进行了如下简化处理：

1）将耙臂前进时推动的浆体圆弧形边缘近似简化为两个剪切平面，如图4所示。

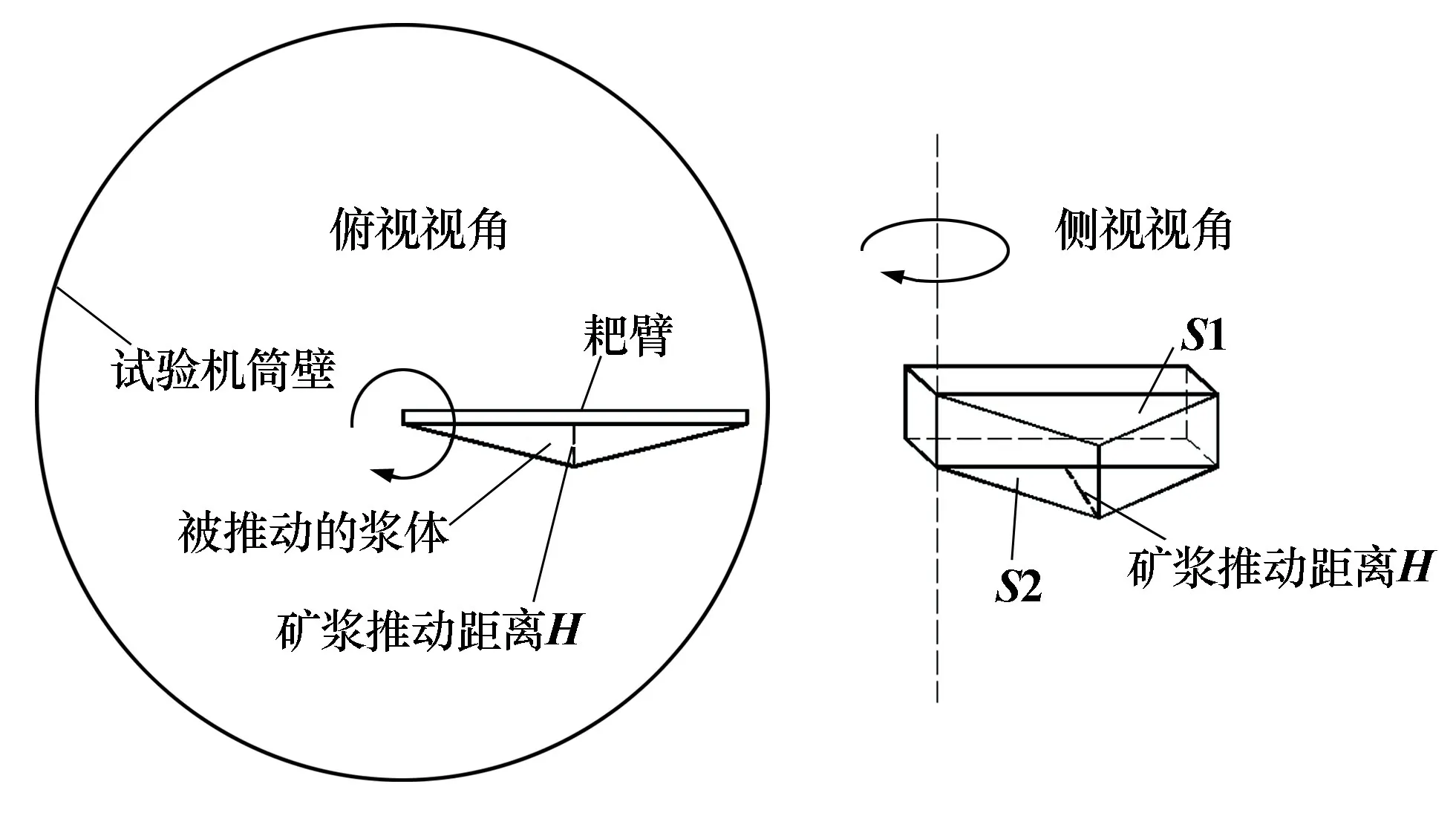
图4 试验机耙臂近似剪切模型示意图

2）这部分被推动的矿浆视为与剪切主体共同运动，内部不发生位移。在运动时与四周矿浆发生剪切作用，即剪切面由上下两个三角形区域及侧部两块矩形组成。

3）定义矿浆推动距离H为单位长度的剪切模型中被推动的浆体边缘中心位置距离剪切主体的距离，mm。

耙臂在运动过程中自身始终与运动方向垂直，因此将耙臂推动的矿浆体视为仅向耙臂推动面的法向方向发生剪切运动，而不发生与耙臂推动面平行方向的剪切运动，剪切面包含上下两个三角形面积及侧面两个矩形剪切面积，转矩力臂长度即为耙臂几何中心与转动圆心的长度：

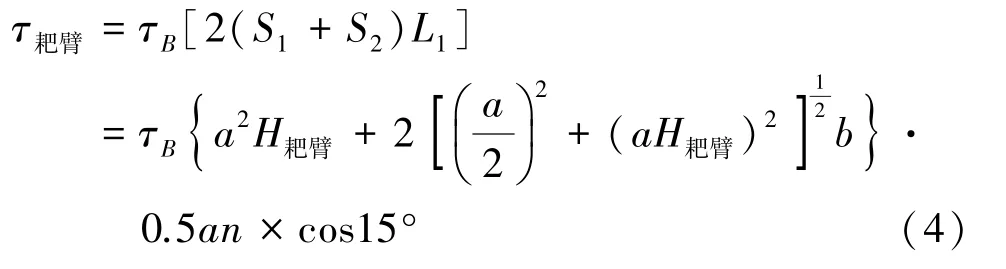
式中τB为浓缩机底部高浓度浆料浓度对应的屈服应力，Pa，这个对应的浓度c B通常大于循环浓度，需通过试验测得；a为耙臂长度，m；b为耙臂高度，m；S1为剪切模型上下方的三角形剪切面积，m2；S2为剪切模型斜侧面的矩形剪切面积，m2；L1为耙臂几何中心转动力臂，m；n为耙臂数量。

将式（2）带入式（4），得到耙臂扭矩关于底部浓度c B、H值及耙臂几何的数学模型：

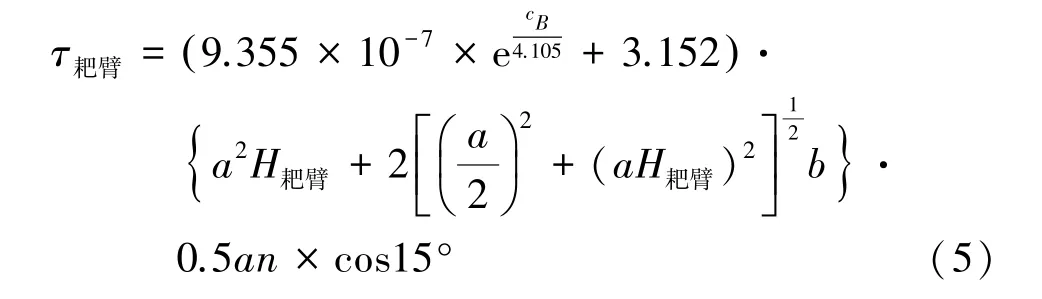
3.3 扭矩数学模型的修正与验证

在试验过程中，耙臂长度a、高度b、耙臂数量n取值分别为0.28 m，0.008 m和2。

H耙臂可通过拟合用耙臂转速v线性表示：

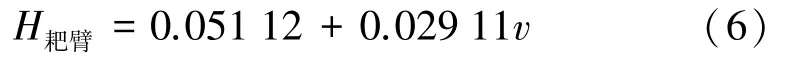
将以上已知参数及修正系数带入式（5）得：

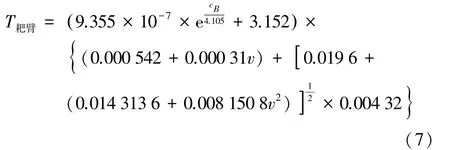
式（7）即为试验机耙臂扭矩T与浓度c B、耙臂转速v之间的数学关系模型。

根据浓缩机实际使用工况，在数学模型验证时采用较高浓度工况即底流循环浓度73%时进行，此时底流浓度为73%，试验测得试验机筒体底部浓度为75%，将计算数据与实测数据进行比对验证，结果如表4所示。由表4可见，数学计算模型对比实际测量值得计算误差整体小于±1%，模型计算数据与实测数据具有较好的吻合度。

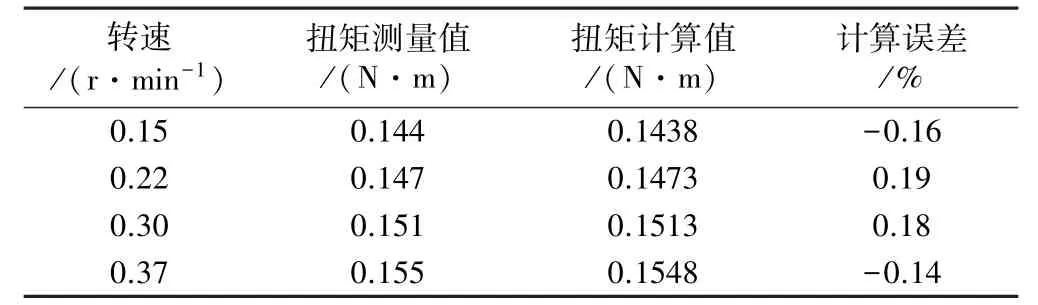
表4 耙臂扭矩计算数据与实测数据对比

4 结 语

1）综合考虑浓缩机在稳定工况中的工作特性，研制了可测耙臂扭矩的实验室浓缩机，并设计了全套试验流程，包括试验物料选择、试验机结构主体及筒体、驱动及控制单元、动态扭矩检测单元、循环给料单元等，形成了一套完整的多因素扭矩测量控制系统，可较为精确地进行扭矩数据的采集。

2）采用Anton Paar MCR72型旋转黏度计研究不同浓度条件下的试验物料的屈服应力，得到试验物料浓度与屈服应力的拟合关系式。

3）建立了耙臂在物料中运动时的剪切物理模型，理论核心为耙臂在运动时被推动的部分浆体与剪切主体共同运动，在运动时与四周矿浆发生剪切作用，剪切面由上下两个三角形区域及侧部两块矩形组成；同时定义了关键参数H——单位长度的剪切模型中被推动并与剪切主体共同运动的矿浆体边缘中心位置距离剪切主体的距离。通过对试验模型进行力学分析，得到试验机耙臂扭矩关于浓度及转速的数学模型。数学计算模型对比实际测量值的计算误差整体小于±1%，计算数据与实测数据较吻合。该方法为浓密机扭矩设计提供了依据。