连铸中间包焊接残余应力数值模拟①
2021-07-12潘龙博谢庆忠刑学强
潘龙博,张 硕,江 济,谢庆忠,刑学强
(安徽马钢重型机械制造有限公司,安徽 马鞍山 243000)
钢的连铸生产设备主要由钢包、中间包和结晶器3个冶金反应器串联布置而成。中间包过程是钢的高效连铸过程中关键生产环节之一,对于提高连铸机生产效率、改善钢坯质量有着重要作用[1-3]。中间包一般采用箱式结构,使用多块钢板拼焊制造。焊缝数量较多且分布密集,造成了较大的焊接残余应力和严重的应力集中。中间包焊接结构整体性强、刚性大,对应力集中因素非常敏感,容易在应力集中位置出现脆性断裂,并且裂纹一旦开始扩展,就难以被止住。焊接残余应力与焊接开裂和变形直接相关,并且影响焊件焊后的承载能力和抵抗破坏能力[4-6]。有限元数值模拟是获得大型焊接结构残余应力最有效的方法之一[7-9]。但目前对于连铸中间包焊接残余应力的数值模拟研究还鲜见相关报道。本文使用有限元法,模拟计算中间包焊接残余应力的分布,为控制焊接接头残余应力、提高焊接质量提供理论依据。
1 数值模拟方法
1.1 焊接工况及材料参数
计算模型为某钢厂连铸中间包,尺寸为5 820 mm×2 140 mm×1 230 mm,包的侧壁斜度13°。中间包由60块钢板和2个吊耳焊接而成,见图1。钢板厚度15~30 mm,包身材质为Q345B,吊耳材质为Q690D,其热学和力学物理性能参数分别见文献[5]和[10]。
焊接方法为CO2气体保护焊,焊接工艺按照JB/T 5000.3—2007《重型机械通用技术条件 第3部分焊接件》标准进行,钢板按GB/T 985.1—2008《气焊、手工电弧焊及气体保护焊焊缝坡口的基本形式与尺寸》加工焊接坡口。采用连续焊缝,焊后退火消除应力。焊接材料使用Φ1.2 mm ER50-6焊丝。焊接使用直流反接,焊前不预热,打底层焊接电流210~240 A,焊接电压24~28 V,保护气体流量8~12 L/min,填充层焊接电流230~260 A,焊接电压26~32 V,保护气体流量10~14 L/min。
中间包共132道焊缝,焊接时先焊内层焊缝,后封装外侧板,最后焊外侧焊缝。焊接时尽量使用平焊及横焊,同一层焊层中,后道焊缝须压前道焊缝宽度的1/3~1/4,且保证焊道之间的圆滑过渡。
1.2 有限元模型
有限元模型使用六面体单元和四面体单元混合网格划分,共44 277个单元,34 626个节点,见图2。为了保证计算精度和提高计算效率,在焊缝及热影响区附近使用较细的网格划分,而在远离焊缝的母材使用较粗的网格。焊缝处网格尺寸为5 mm×6.67 mm×53.6 mm。
焊接热过程的控制方程为Fourier导热方程,对于直角坐标系,有:
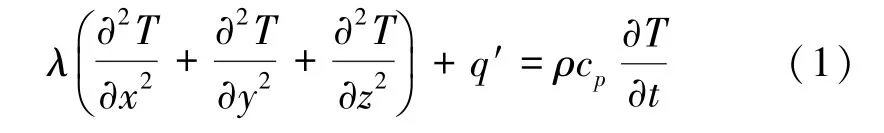
式中λ为材料的导热系数;T为温度;t为时间;ρ为材料密度;c p为材料的定压比热;q′为内热源的热流密度。由于计算模型焊缝较多,为了简化计算,使用均匀热源模型,即认为在每道焊道中焊接热源同时施加到焊缝中。焊接热源的热流密度与时间成倒三角分布,以模拟电弧的接近和离开,热流密度D f[11]为:

式中U为焊接电压;I为焊接电流;η为电弧热效率;V p为受焊接热源影响的焊缝金属的体积。
焊接热过程使焊接区域形成热应变,焊接应力/应变场的控制方程为广义的Hooke定律:
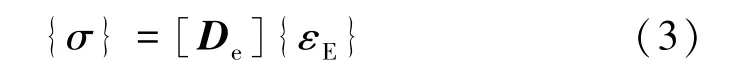
式中{σ}为应力;{εE}为弹性应变;[De]为弹性矩阵。在热⁃弹塑性有限元分析中,一般使用增量理论计算。总应变增量dε可表示为:
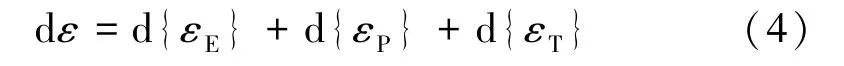
式中等号右边各项分别为由弹性应变、塑性应变、热应变引起的应变增量。对于金属材料,可以认为热膨胀是各项同性的:

式中α为材料的热膨胀系数。计算中,使用Mises屈服准则:

式中为等效应力;σs为材料的屈服极限。流动法则为Prandtl⁃Reuss塑性流动增量理论:
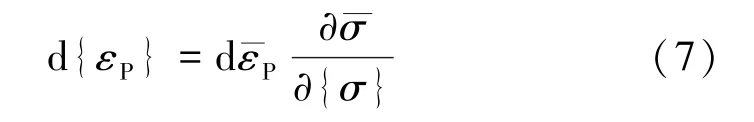
2 结果与讨论
中间包焊接残余应力分布如图3所示。可以看出,在焊缝形成了较大的残余应力,残余应力峰值约672 MPa,已经达到材料屈服极限。在中间包吊耳和背部应力集中较为明显,说明在这些位置焊接裂纹开裂较大。中间包背部为多块钢板拼焊而成的箱体结构,焊缝集中,存在着显著的残余应力。

图3 焊接残余应力分布
焊接裂纹倾向除了与应力大小有关,还与应力方向有关。一般认为只有在拉应力作用下,裂纹才会扩展,而残余压应力可以提高工件强度、降低开裂倾向。为了研究中间包背部残余应力分布,沿中间包背部箱式结构中心线L1测量残余应力,取样点见图4,各点残余应力分布如图5所示。W1~W11位置分别为背板与腹板的连接焊缝位置。从图5(a)可以看出,焊接残余应力关于中间包中面近似成对称分布,在焊缝位置形成了很高的残余应力,并且在中部和两侧焊缝残余应力最高,等效应力可达约400 MPa,而其他焊缝残余应力相对较低,等效应力约300 MPa。其原因可能是中间包背部使用多块焊板拼焊而成,随着焊接的进行,应力逐渐累积,在中心和两侧拘束最大,焊缝无法自由变形,因此形成了更高的残余应力,而其余位置焊缝由于可以向两侧变形,拘束较小,残余应力也较低。从图5(b)可以看出,最大主应力分布趋势与等效应力类似,在焊缝处形成了很大的拉应力,而在母材处应力较小,并在部分母材中形成了一定的压应力。中间包中心面和两侧边缘处焊缝最大主应力最高,可达约350 MPa,而其他位置焊缝主应力略低,约300 MPa。因此可以推测,在中间包背部中心面和两侧边缘处开裂倾向较大,实际中间包焊接时也发现在中间包背部中心面附近焊缝出现了较多的裂纹。

图4 残余应力测量位置示意

图5 中间包背部残余应力分布
中间包侧面残余应力分布如图6所示。从图6(a)可以看出,中间包侧面钢板内存在很大残余应力,等效应力最高可达约450 MPa。吊耳内残余应力很低的原因是,为了简化计算将吊耳作为一个整体,没有计算吊耳与钢管之间的焊缝。从图6(b)可以看出,与中间包背部钢板不同,在整个侧面钢板内均出现了很高的残余应力,其原因在于侧面钢板尺寸较小,钢板大部分区域在焊接热循环的作用下都被加热到了较高温度,产生了较大的塑性变形。
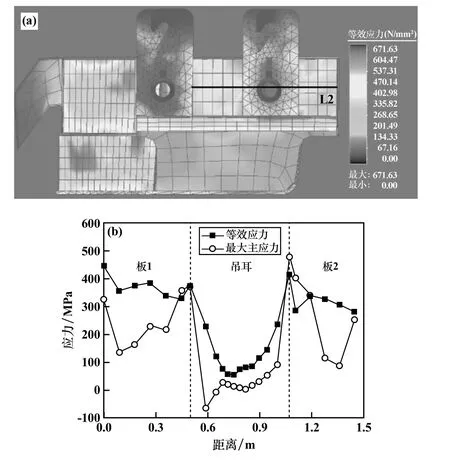
图6 中间包侧面残余应力分布
3 结 论
1)建立了中间包焊接有限元计算模型,使用该模型模拟了中间包焊接残余应力分布。中间包在焊缝形成了较大的残余应力,残余应力峰值约672 MPa,已经达到材料屈服极限。在中间包吊耳和背部应力集中较为明显,说明在这些位置焊接裂纹开裂较大。
2)在中间包背部,焊接残余应力关于中间包中面近似成对称分布,在焊缝位置形成了很高的残余应力,并且在中部和两侧焊缝残余应力最高,等效应力可达约400 MPa,而其它焊缝残余应力相对较低,等效应力约300 MPa。
3)中间包侧面吊耳与钢板连接处焊缝出现了较大的应力集中,等效应力最高可达约450 MPa。
