基于运动约束抑制惯导误差的高速列车隧道内定位方法

孙振乾, 唐康华, 吴美平, 郭妍, 王雪莹

(国防科技大学 智能科学学院, 湖南 长沙 410073)

随着中国高速铁路网的布局更加完善，在网运行的列车数量越来越多，发车频次越来越高，这就需要给运行控制系统提供更加精准的位置、速度及姿态信息,以实现列车的控制、调度与监测[1]。列车运行过程中会出现GNSS信号遮挡、城市及山间峡谷可观测的卫星少,特别是在长隧道内卫星信号长时间缺失，对定位系统是个很大挑战[3]。

传统列车定位系统采用测速测距方式，定位精度差，提供的列车信息有限，系统维护复杂[4]，设备成本高，且难以解决长隧道内的定位问题，已无法满足高速列车定位需求。随着MEMS惯性器件的精度越来越高，可靠性和成本优势让其在车载领域应用广泛[5]。GNSS星基增强技术将卫星定位精度提高到亚米级[6]。INS和GNSS良好的互补性，使其成为高铁定位的核心，但在长隧道内,GNSS信号缺失,仅依赖MIMU定位精度难以保证[7-9]。

近年来，针对隧道内无GNSS信号时列车定位研究成为热点。目前主要有2种方式：①在系统中加入额外传感器，主要有激光雷达、多普勒测速仪、气压高度计、里程计、相机、无线定位、地图匹配、RFID等[4]，与INS组合导航实现列车定位。但是，加多余传感器会提高系统的成本和实现难度，增加维修保养负担。②利用轨道或列车运动信息约束抑制惯导误差发散保证列车在隧道内的定位精度。王鹏飞等提出了基于列车运动模型和轨道约束的方法[10]，在GNSS缺失40 s时水平定位误差达21.2 m。梁飞采用列车运动模型和陀螺仪组合的方法对卫星盲区的列车定位[11]，卫星信号缺失10 s后，水平误差高达31 m。杨菊花等人采用列车运动约束来抑制惯导的误差[12]，明显提高了列车导航精度。但在运动约束模型中没有考虑安装角影响，50 s内水平定位误差为12.6 m，水平速度误差约为0.71 m/s，精度有待进一步提升。在毫米级精度要求的轨道检测领域，陈起金等人设计了基于高精度激光INS/GNSS组合导航的轨检小车[1]，使用运动约束提高系统在GNSS信号受干扰时的精度。由于没有考虑安装角，对系统精度的提升有限。张全等人对上述系统进行了改进，在运动约束模型中考虑了安装角[13]，但是没有提到怎么得到安装角。朱峰等人在无GNSS信号时，通过事后数据处理利用相似旋转的方法得到安装角[14]，但安装角并未被用于运动约束。准确得到MIMU的安装角，是提高运动约束效果的关键[9,15]。

高速列车在长隧道内GNSS信号缺失且其他可用信息少，现有方法定位精度低，隧道内建立精确的电子地图和布设高精度参考点都很难实现。针对此，在不增加额外传感器的情况下，本文提出CIAMC-INS方法。由于安装角的存在，使得相对车体m系的车辆运动约束假设在惯导系统的b系中不再成立。该方法先首在考虑MIMU安装角的基础上建立了运动约束模型；其次通过分析列车转弯对运动约束模型的影响，得到运动约束的使用条件；然后在GNSS信号良好且满足运动约束使用条件时，在线估计MIMU的安装角。最后在GNSS缺失的隧道内，将估计的安装角用于运动约束辅助INS定位。实验结果表明，考虑安装角的运动约束方法对纯惯导误差的抑制作用更明显，列车在隧道内的定位精度得到明显提高，验证了方法的有效性。

1 车辆运动学约束

1.1 列车运动约束关系

定义列车车体坐标系为m系,原点为列车车厢中心,x,y轴分别指向列车的右向、前向,z轴与x,y轴构成右手直角坐标系。定义MIMU坐标系为b系,安装过程中b系的x,y,z轴尽量和m系的x,y,z轴朝向保持一致,保证安装角为小角度。

(1)

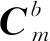
根据文献[17]中的结论,横滚安装角对运动约束没有影响。一旦MIMU固定在列车上,安装角误差可以视为小角度随机常数。不考虑δaγ的影响,将δaθ和δaψ扩张成三维向量形式

δa=[δaθ0δaψ]T

(2)

安装角余弦矩阵误差可表示为

(3)

1.2 列车转弯对运动约束的影响

高铁轨道的曲线线路一般由直线、缓和曲线、圆曲线组成[16],如图1所示。在车体转弯的过程中,由于MIMU安装位置与载车旋转中心存在杆臂,在MIMU安装处存在杆臂速度[18-19]。

图1 轨道曲线线路平面图

列车在前向牵引力、轨道、转向架、车轮等机构的配合下实现转弯[20],允许车箱和转向架之间有一定程度旋转[9],转向架的实物如图2所示。

图2 转向架实物图

为了简化分析,选择图1中的S段,也即列车从B点到C点左转弯,转弯模型如图3所示。转向架行驶在半径为R的列车轨道上,且行驶方向与轨道近似相切。P1和P2为前后转向架的插销中点,车厢在通过两点的割线上。

图3 列车转弯几何分析

因此,列车转向架的速度方向和车厢轴线之间存在偏差角β[9],由几何关系可得

(4)

式中,d为P1和P2点之间的距离。

转弯过程中,车厢绕O1点旋转,旋转角速度为

(5)

式中,vD1为前转向架插销的速度。

侧向速度为零的假设在转向架坐标系中的中心点P1处依然成立,由于车厢绕O1的旋转,在m系中此假设不在成立。设MIMU安装在P1点,此时,MIMU在m系中的速度为

(6)

设列车速度为350 km/h,2个转向架中心点距离为20 m,转弯半径为5 000 m[16],由于转弯引起的侧向速度为

(7)

这将严重影响卡尔曼滤波器状态估计精度,甚至导致滤波器发散。

将(5)式带入(6)式可得

(8)

式中,ωz为z轴陀螺的输出。

在实际行驶过程中,列车的机动转弯将更加复杂,前后转向架的转弯角速度和车厢的旋转中心均不固定。很难建立精确的侧向速度补偿模型。但(8)式仍然为判断侧向速度为零的假设是否成立提供了理论依据。

1.3 运动学约束的阈值

为了减小水平转向机动对运动约束的不利影响,以车体天向陀螺输出的转弯角速率为判断否可使用运动约束的条件,表述为

|ωz-ωz-bias|<ωz-threshold

(9)

式中:ωz为MIMU的z轴陀螺输出;ωz-bias为z轴陀螺的零偏;ωz-threshold为设定的判定阈值,高铁运行比较平稳且转弯少,可以根据实测数据设定阈值。实验采集的列车运行过程中z轴陀螺数据如图4所示。

图4 z轴陀螺测量数据

(10)

式中,η为阈值的调节系数,可视运动状况及精度要求适当选取。

2 组合导航模型及算法流程

本节根据对GNSS信号是否可用和列车运行状态的判断,设计相应的滤波模型,并给出算法流程。

2.1 MIMU/GNSS松组合模型

当列车转向且GNSS信号良好时,运动约束不可用。列车定位采用15维MIMU/GNSS松组合EKF滤波器,依据惯导误差传播模型,忽略安装杆臂的影响,系统的15维状态误差向量定义为

X1=

(11)

式中：φn为姿态误差；δvn为速度误差；δPn为位置误差；δεb为陀螺在b系中的零漂误差；δb为加速度计在b系中的零偏误差。

系统状态方程为

(12)

式中：FINS为系统状态转移矩阵；G1为噪声转移矩阵；W1为过程噪声向量。

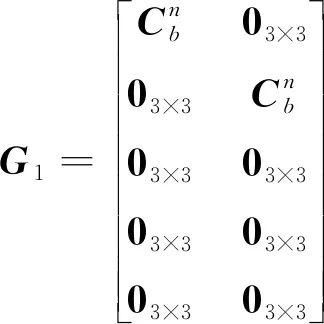
(13)

(14)

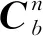
GNSS/MIMU组合的观测模型表示为

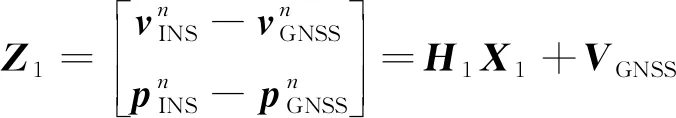
(15)

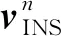
(16)

2.2 MIMU/GNSS/运动约束组合模型

当运动约束和GNSS均可用时,可构建滤波器在线估计MIMU相对车体的安装角。将俯仰角安装角误差δaθ和航向角安装角误差δaψ也扩充为误差状态量,17维状态变量为

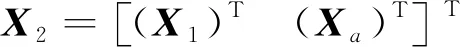
(17)

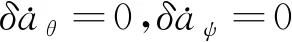
(18)

系统状态方程为

(19)

式中,Fa=02×2,Ga=I2×2,Wa为安装角误差噪声。

结合(3)式,(1)式的全微分为

(20)

由列车的运动约束构成的观测方程为

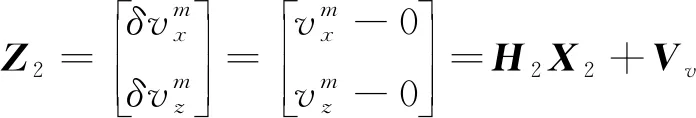
(21)

(22)

式中,Mi(k,×)为矩阵Mi的第k(k=1,2,3)行的所有元素。

GNSS和运动约束的联合观测方程为

(23)

令运动约束的观测频率为1 Hz,且与GNSS观测数据同步。

2.3 MIMU/MC组合模型

在铁路线路设计中,隧道内尽量避免设置曲线轨道,即便在特殊情况下设置曲线,曲线的长度会尽量小[16]。因此,在隧道中若存在短时曲线转弯,可依靠纯惯性导航实现定位。在隧道中装误差角不再估计,系统的状态方程如(12)式所示。

将在隧道外已经估计得到的安装角作为已知常值带入(20)式,可得

(24)

由运动约束提供的观测方程为

(25)

(22)式改写为

(26)

2.4 定位算法的流程

根据列车运行状态和GNSS数据的观测环境,设计了3种滤波算法模,如图5所示。在GNSS信号良好且满足运动约束条件时,17维EKF1使用GNSS和运动约束提供观测,估计各状态量,确定MIMU安装角。在无GNSS信号且满足运动约束条件时,15维EKF2仅使用车辆运动学约束提供观测,安装角为EKF1的估计值。在GNSS信号良好但不满足运动约束条件时,15维EKF3仅使用GNSS速度位置作为观测。当定位模式发生变化时,公共状态的估计值及其误差协方差阵从老算法直接传递给新算法,其他量不更新或者重置[21]。

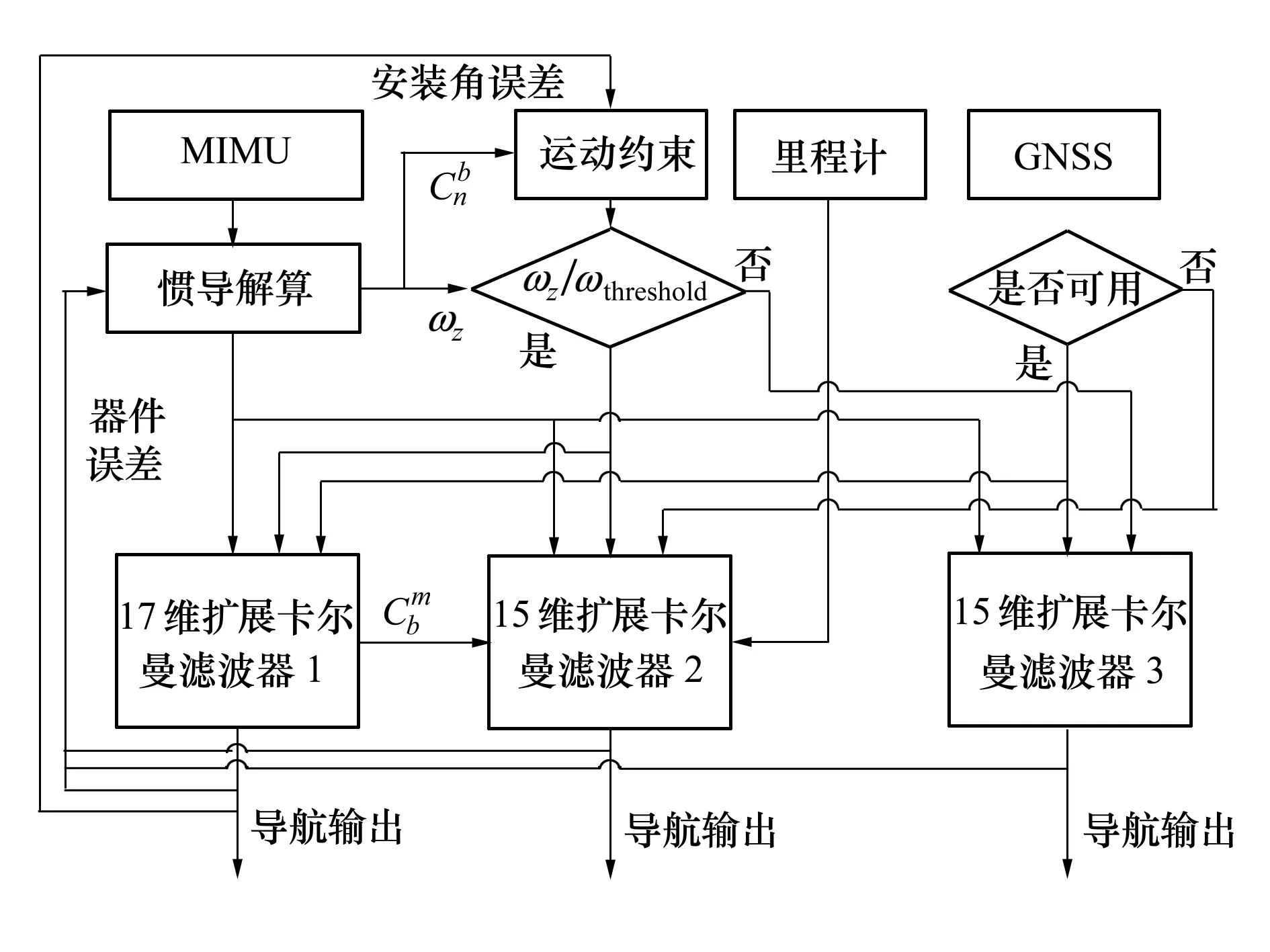
图5 定位算法流程图

3 试验说明

高铁定位系统主要由MIMU(50 Hz)、GNSS接收机(1 Hz)、Cortex-A9+FPGA硬件平台等部件组成。组合导航模块固定在前转向架中心附近的车厢地板上,GNSS接收机固定在组合导航模块正上方的车厢顶部,PC机通过串口接收并存储试验数据,整个系统组成如图6所示。

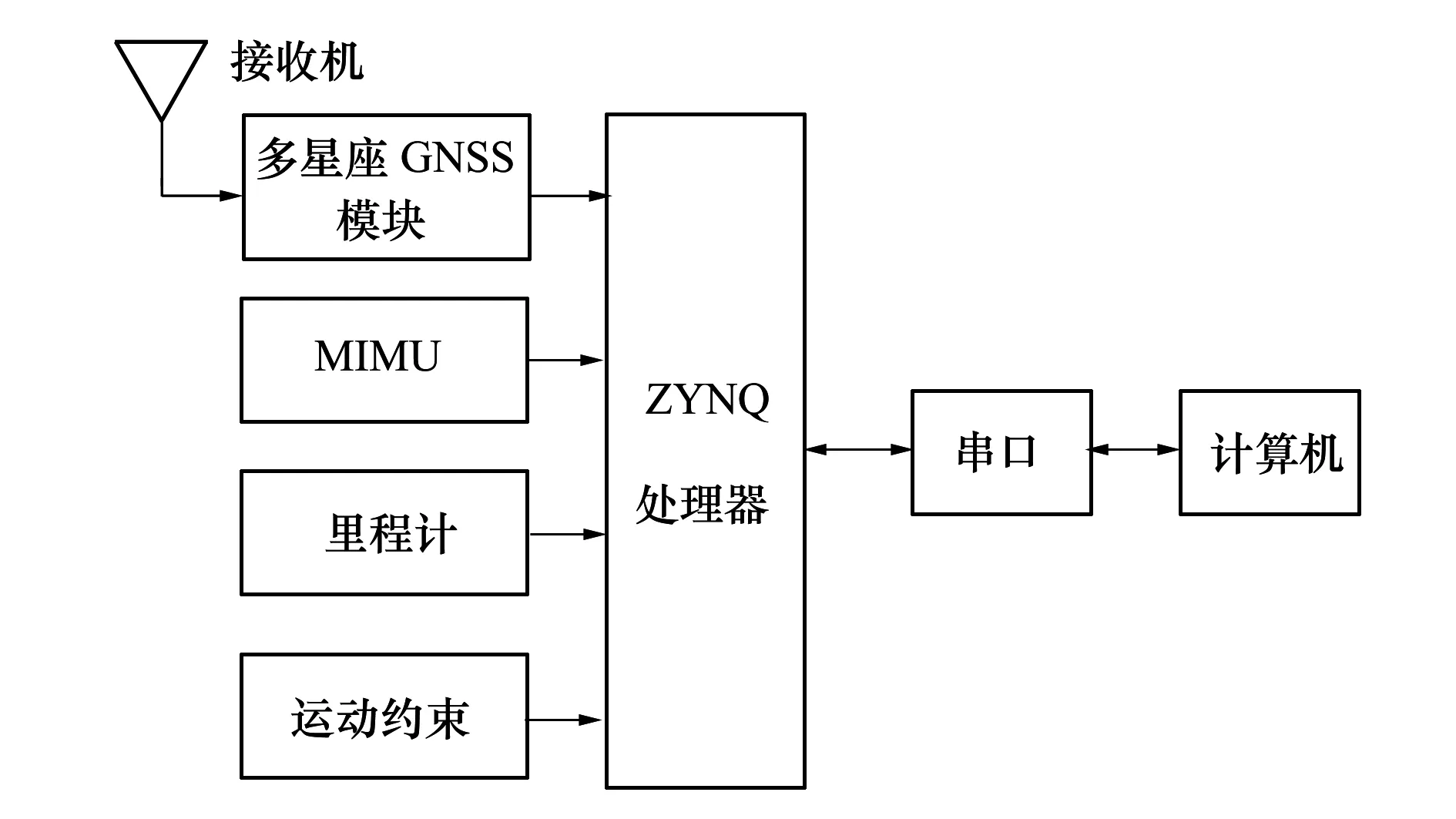
图6 组合导航及数据采集系统

4 试验结果与分析

4.1 MIMU安装角估计结果

列车运行在卫星信号良好且满足使用运动约束条件的情况下,对安装角估计,其他情况下,安装角保持原值不更新,安装角估计的结果如图7所示。

图7 MIMU安装角估计

在启动初期,加速度不稳定且速度很小,安装角估计值波动较大,安装角的可观测性与速度和加速度紧密相关。在进入稳定加速阶段,安装角的估计有较快收敛,在匀速行驶阶段安装角变化较小。相比俯仰安装角,航向安装角收敛速度较慢,与列车缺少航向机动及惯导航向角初始化的精度低有关,姿态失准角与安装角存在一定的耦合关系。

4.2 隧道出口处定位结果

列车进入隧道GNSS信号完全丢失,出隧道后接收机需要对GNSS信号再次捕获、跟踪,在隧道出口附近的参考点处,仍无法定位。在途中的隧道段分别采用CIAMC-INS算法、传统的不考虑安装角的运动约束抑制惯导(traditional motion constraints suppress INS error,TMC-INS)、P-INS 3种算法定位。以隧道入口最后一个GNSS定位点为参考原点,绘制列车运行轨迹,如图8至9所示。红色标识点为参考点,图8为参考点11,图9中从左到右依次为参考点21,22,23,24。两隧道出口参考点处水平定位误差统计在表1和表2中。

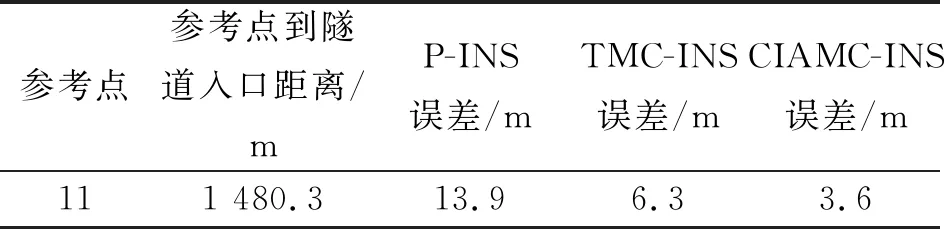
表1 1 412 m隧道出口参考点处水平定位误差统计

表2 9 063 m隧道口参考点处水平定位误差统计

图8 1 412 m隧道出口处定位轨迹

图9 9 063 m隧道出口处定位轨迹

在1 412 m长隧道出口11号参考点处,3种定位算法的误差百分比分别为:0.94%,0.41%,0.24%。CIAMC-INS算法在隧道口参考点处水平定位误差分别比P-INS算法和TMC-INS算法减小了74.1%,38.1%。

9 063 m长隧道中包含一段长约800 m的转弯隧道。3种定位算法的平均误差百分比分别为:3.23%,0.80%,0.47%。CIAMC-INS算法在隧道口参考点处水平定位误差分别比P-INS和TMC-INS减小了84.2%,36.3%。

从统计结果可知,列车在隧道段运动约束方法明显抑制了惯性导航系统定位误差的发散。考虑MIMU安装角影响的CIAMC-INS算法,可以进一步增强抑制作用,提高定位精度。

4.3 隧道内定位结果

因隧道内无定位基准,为进一步分析CIAMC-INS算法在隧道内的有效性,选择一段开阔地带,以平滑后的GNSS/MIMU组合导航定位结果为基准,将GNSS数据断开100 s,以模拟隧道内GNSS信号缺失环境。卫星断开时间内列车直线行驶9 515 m。图10和图11分别显示了3种算法的东向和北向位置误差,图12至13分别显示了3种算法的东向和北向速度误差,图14显示了3种算法的航向角误差。表3列出了3种算法的水平位置、水平速度、航向角的100 s误差及均方根误差。

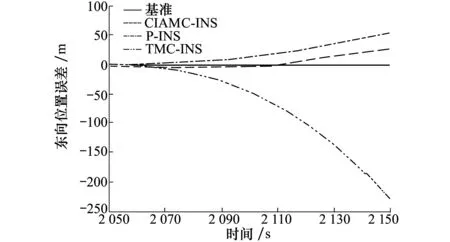
图10 东向位置误差

图11 北向位置误差

图12 东向速度误差 图13 北向速度误差 图14 航向角误差

从表3的统计结果可知,CIAMC-INS算法相比P-INS和TMC-INS算法,水平位置误差、水平速度位置误差和航向角误差均大幅减小。

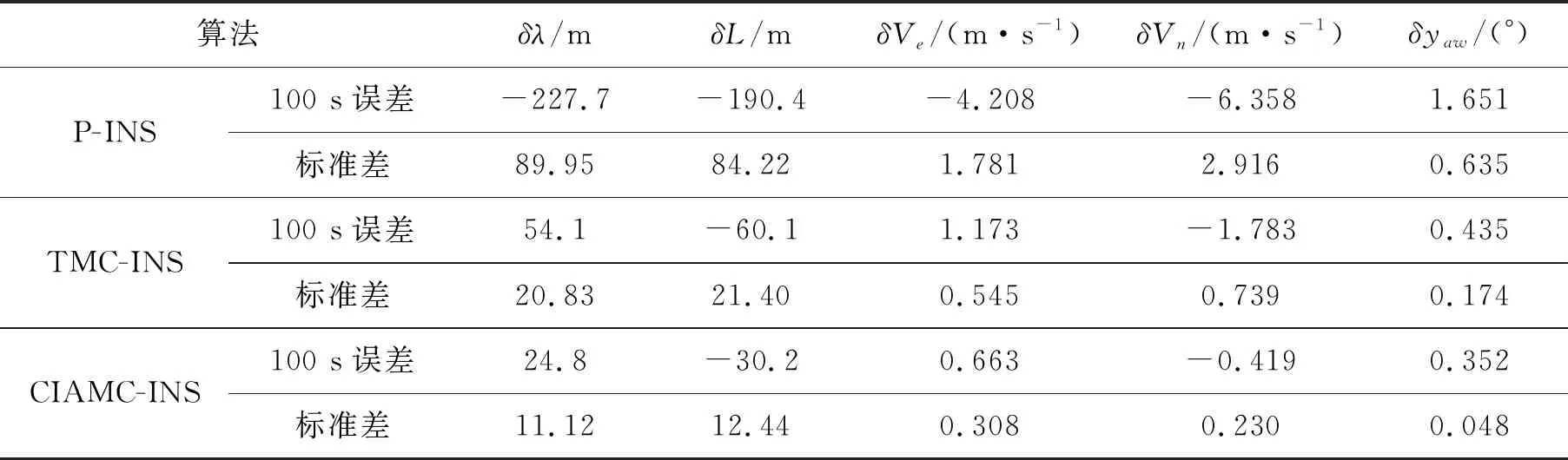
表3 隧道口定位误差统计

在卫星信号缺失时,2种运动约束算法对惯导系统的水平位置、水平速度及航向角的误差发散均有一定程度的抑制作用, CIAMC-INS算法对误差的抑制作用更明显。由于采用的惯性器件的精度较低,列车在隧道中缺少机动影响误差估计的效果,且没有约束列车前向速度等原因, CIAMC-INS算法不能完全消除惯导系统误差发散,仍然随时间存在一定程度的误差累积。列车车轮安装有轮式脉冲速度传感器,在将来的工作中可用于约束列车的前向速度,进一步提高定位的精度。

5 结 论

本文针对高速列车在隧道环境卫星信号缺失时定位精度差的问题,在不增加额外传感器的情况下,提出了考虑MIMU相对车体安装角的CIAMC-INS算法。在沈阳至朝阳段进行了高铁车载试验,对比分析了采用P-INS,TMC-INS,CIAMC-INS 3种算法定位结果。试验结果表明,在GNSS观测良好和满足运动约束条件时,MIMU在列车上的安装角可以通过扩展卡尔曼滤波器有效估计;在无GNSS信号的隧道段,CIAMC-INS算法对惯导水平位置误差、水平速度误差及航向角的误差抑制作用比TMC-INS算法更加明显。在不添加额外传感器的情况下,通过9 063 m长且中间有长约800 m弯曲段的隧道,在无GNSS情况下行驶9 163 m的水平定位误差大概为43.3 m。人为断开GNSS情况下,列车直线行驶9 515 m后,水平定位误差约为38.9 m。试验结果表明,在包含转弯的隧道和直隧道内,定位精度均得到大幅提高,曲线隧道内精度稍差,验证了提出算法的有效性,具有重要的应用价值。