基于PCA-LASSO方法的行业市盈率预测及影响因素分析

孟洁莹

摘 要：本文基于分行业的横截面财务数据分析影响市盈率的主要因素，提出了PCA-LASSO模型及其精简模型方法，并对市盈率进行样本外预测，同时与传统的线性回归模型及LASSO回归模型的结果进行了比较。研究表明，在行业市盈率的样本外预测方面，所提出的PCA-LASSO模型及其精简模型方法明显优于已有的两种研究方法。所提模型方法融合了主成分回归和LASSO回归的优点，既完全消除了多重共线性又实现了对重要变量的选择，同时具有更高的预测精度，所提方法具有普遍适用性。

關键词：PCA-LASSO模型;市盈率;影响因素;样本外预测

中图分类号：F832 文献标识码：A 文章编号：2096-0298（2021）05（a）--03

市盈率（P/E ratio）又称为本益比，指每股市价除以每股盈利（EPS），是判断股票价值、评估股价水平是否合理的最简单直观、最常用的指标之一。Graham 和 Dodder的经典著作《Security Analysis》[1]在其1934年的第一版中已经清晰地给出了市盈率的概念。Whitbeck和Kisor（1963）[2]从股票定价模型出发，认为市盈率与股利支付率成反比，与盈利增长率、风险成正比，与传统股价定价模型得出的结论一致。Basu（1977）[3]通过实证研究验证了市盈率是影响股票收益的重要指标之一。

国内的学者对市盈率的影响因素作了大量的研究。王振鹏（2016）[4]基于上证50样本股2008到2013年的数据，利用线性回归模型研究了上市公司市盈率和七个指标因素之间的关系。李杨和曾宪斌（2014）[5]分别考虑了LASSO，Adaptive LASSO，Bridge和SCAD四种惩罚函数模型并进行比较，在面板数据框架下应用惩罚似然方法对机械设计仪表板块的上市公司市盈率的影响因素进行了选择。

综合国内外学者的研究，本文的研究不仅关注影响市盈率的重要因素，更注重对市盈率样本外预测精度的提升。在研究方法上，本文将提出全新的PCA-LASSO的模型方法，它是一种融合了主成分回归和LASSO压缩的方法，从而实现了估计过程中对多重共线性问题的完全解决及对显著影响因素的快速选择。在此基础上，我们还进一步提出了PCA-LASSO的精简模型方法，一方面优化了模型的预测精度，另一方面更加明确了影响市盈率的重要因素。

1 模型方法

1.1 PCA-LASSO模型

记k个解释变量的观测数据矩阵为[Xn×k]，因变量的观测向量为[Yn×1]。 PCA-LASSO模型方法可以分两步实现：第一步，对解释变量进行主成分分析，得主成分矩阵及因子载荷矩阵：

其中，[PCn×k]为主成分矩阵，包含k个主成分列向量，[Ak×k]为因子载荷矩阵。这k个主成分之间是正交的，不再具有相关性，但还需要通过进一步回归分析来确定这些主成分对因变量影响的重要程度。第二步，利用因变量Y对第一步中得到的k个主成分进行LASSO回归，并基于交互验证CV（cross-validation）的方法确定最优压缩程度，从而选择对因变量有重要影响的主成分，得到如下基于LASSO的主成分回归模型：

其中，β^k×1pcaLAS中的部分回归系数被压缩为零，从而实现对重要主成分的自动选择。

在上述PCA-LASSO回归模型的估计过程中，完全消除了多重共线性对回归结果的影响，而且可以准确度量每一个解释变量对因变量的影响。由式（1）和（2）可得：

1.2 PCA-LASSO的精简模型

注意到，上述最终的PCA-LASSO模型式（3）中回归系数向量中一般不会再有回归系数完全等于零，即所有的解释变量都参与了对因变量的解释和预测。当模型中解释变量数目较多而样本量较小时，一个一般的常识是解释变量过多反而会降低模型的预测精度。因此，我们可以在PCA-LASSO模型的基础上寻找一个最优的精简模型，具体做法如下：

（1）把所有的解释变量按照其在φ^k×1中对应的回归系数绝对值的大小顺序，由大到小排列。

（2）利用因变量Y和最重要的一个解释变量及其在φ^k×1中对应的回归系数，构建第一个回归方程，在训练数据及内，利用CV的方法计算预测误差RMSE。

（3）在模型中依次引入一个较重要的变量及其回归系数，将一共得到k个回归方程，对每一个方程在训练数据集内利用CV方法计算其RMSE。

（4）在k个回归方程中，选择RMSE最小的模型，作为PCA-LASSO的精简模型。

2 变量选取及数据来源

综合相关金融理论和研究文献，我们对可能影响市盈率的指标进行了初步选择，对数据做了预处理，为模型分析做准备。

2.1 变量选取

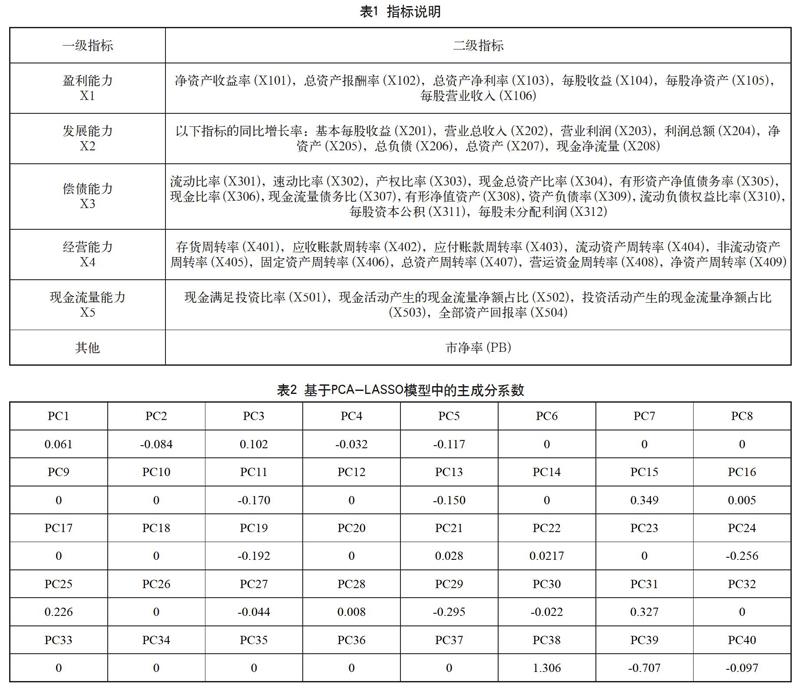
本文选取的指标影响因素分为以下6个方面，即6个一级指标，二级指标共计40个。具体指标如表1所示。

2.2 样本选择和数据来源

本文根据证监会行业分类标准，选择了制造业的电子类，以107家上市公司为研究对象，并分别选取了2020年第二个季度的数据用于模型估计，2020年第三个季度的数据用于样本外预测和模型评价。在市盈率数据的选择上，本文选用的是中证发布的静态市盈率，计算公式为股价除以去年每股收益。市盈率数据选用季度财务报告发布月份的最后一天数据（数据来源于同花顺金融数据终端iFinD）。

3 实证分析

3.1 样本内模型参数估计

（1）基于PCA-LASSO模型的样本内模型估计：利用模型思路，先进行主成分分析，得到40个主成分向量及因子载荷矩阵，再利用LASSO回归选择对因变量有重要影响的主成分。后基于该最优主成分回归的结果，得到市盈率PE与各主成分的回归结果，即β^k×1pcaLAS的数值。在β^k×1pcaLAS中，很多回归系数被压缩为零，从而完成了对影响市盈率的主成分的选择，具体结果如表2所示。

由表2可知，有22个对PE有重要影响的主成分被保留下来，其他主成分系数都被压为0。基于因子载荷矩阵及最优LASSO回归系数，可得式（3）中的系数向量φ^k×1，它直接度量了40个指标对Y的影响。根据回归系数绝对值大小对这40个系数进行排序，依据排序结果可知，电子类市盈率的影响较大的前十个财务指标依次是X103，X303，X305，X102，PB，X301，X306，X302，X104，X201。

依据回归系数，可以写出市盈率PE与相应的40个指标的回归方程：

（2）PCA-LASSO精简模型的估计结果：基于上一节中对PCA-LASSO精简模型的构建思路，利用训练数据集，计算每一个测试模型的MSE，经计算，当模型中包含前16个指标时，MSE达到最小，从而得到如下模型：

PE=-1.03X103-0.79X303+0.66X305+0.45X102+0.31PB-0.211X301-0.211X106+0.18X302+0.17X104+0.16X201+0.14X204+0.13X105-0.12X312-0.12X307+0.11X404+0.11X502 （M4）

该PCA-LASSO精简模型给出了最终影响市盈率的16个指标，以及它们对市盈率影响的方向和程度。

3.2 样本外模型预测与评价

预测的准确与否是评价模型好坏的一个标准。因此，本部分分别将多元回归模型、LASSO模型、PCA-LASSO模型及其精简模型应用于样本外的测试数据集，根据预测的结果和实际的结果进行比较，以评价模型的有效性。本部分采用均方根误差（RMSE）来衡量预测模型的精度。

利用基于訓练数据得到的四个回归方程（M1）-（M4）分别对测试数据集进行预测，预测的均方根误差分别记为RMSE1到RMSE4，具体结果如表3所示。

由表3可知，PCA-LASSO模型的预测效果明显优于LASSO模型及一般的线性回归模型;利用精简模型不但可以完成对影响PE的重要指标的选择，还可以取得略优于PCA-LASSO模型的预测效果。

4 结语

本文提出了PCA-LASSO模型及其精简模型的方法，基于分行业的横截面数据来研究市盈率的影响因素以及对市盈率进行预测。并对2020年电子类107家上市公司的市盈率基于横截面指标数据进行了样本内估计和样本外预测，得到了影响电子类上市公司市盈率的重要因素，对于投资决策具有较好的参考和借鉴意义。

参考文献

Graham B， Dodd D L. Security Analysis （1th ed.） [M]. Mcgraw-Hill Companies Inc，1934.

Whitbeck V S， Kisor M. A New Tool in Investment Decision-Making[J]. Financial Analysts Journal，1963，19（03）：55-62.

Basu S. Investment Performance of Common Stocks in Relation to Their Price-Earnings Ratios： A Test of the Efficient Market Hypothesis[J]. Journal of Finance， 1977， 32（03）：663-682.

王振鹏.中国上市公司市盈率的影响因素研究——基于2008—2013年上证50指样本股数据[J].金融经济月刊，2016（01）：54-58.

李扬，曾宪斌.面板数据模型的惩罚似然变量选择方法研究[J].统计研究，2014，31（03）：83-89.