四配位铂磷光发射体结构与光物理性质关系的理论研究

王 建，张红星

（吉林大学理论化学研究所,长春130021）

Phosphorescent materials based on transition metal complexes，particularly Pt（Ⅱ）complexes，have attracted both academic and industrial attentions due to their low-cost fabrication and highly efficient electron luminescent emitters in organic light emitting diodes（OLED）［1，2］.Professor Che has developed a novel type of Pt（Ⅱ）complexes with OˆNˆCˆN ligand and has successfully assembled a series of highly efficient OLEDs［3—7］.With the help of transient state spectroscopy technics，a fundamental understanding of the excited state properties is established and the photo-deactivation pathway is identified.But the investigation on the structural-photophysical relationship at the level of modern quantum mechanics is quite limited and a detailed description of the competing mechanisms of radiative and non-radiative nature has therefore remained elusive［8—11］.It is generally believed that spin-orbit coupling（SOC）induces fast intersystem crossing（ISC）and phosphorescent decay in organometallic complexes［12］.The recent improvements in theoretical approaches have extended the applications from a qualitative assignment of the absorption and emission color and corresponding transition character to a quantitative interpretation of both emission spectroscopy and excited state decay pathway by including calculations of the SOC integral，radiative lifetime and rate constants with the scalar relativistic or pseudo-relativistic corrections of heavy element relativistic effects［13—17］.With the aim of gaining depth-insight into the basic rules in the material chemistry，in current contribution，we try to evaluate the possible ISC channels by calculating the SOC integral for three Pt（Ⅱ）complexes supported by OˆNˆCˆN tetradentate ligands，as shown in Fig.1.Through rigorous density functional theory calculations，not only the radiative decay rate constant and non-radiative decay rate are well reproduced，but also a good interpretation of the difference in quantum efficiency among these three Pt（Ⅱ）complexes is provided based on the analysis and discussion of excited state geometry and energy levels，as well as ISC channels.

Fig.1 Chemical structures of tetra-Pt complexes

1 Computational Details and Theoretical Background

We perform geometry optimizations for ground（S0）and excited states（T1），followed by harmonic vibrational frequencies calculation at PBE0/LanL2TZ（f）；6-311G（d，p）/PCM-CH2Cl2level of theory.TheS0andT1states are respectively described at the restricted and unrestricted density functional theory（DFT）levels［18—20］.The energy levels and the transition properties of the singlet and triplet excited state were calculated with TD-DFT［21—23］approach at TD-BMK/LanL2TZ（f）；6-311（d，p）/PCM-CH2Cl2level of theory.All the above calculations were completed with Gaussian16 program［24］.

The spin-orbit-coupling（SOC）effect splits theT1state into three sub-states that are separated in energy in the absence of an applied field.This splitting is referred as the zero-field splitting.The radiative ratekiand the radiative lifetimeτifrom the sub-statei（i=1，2，3）of theT1state to the singlet ground state can be evaluated from the transition energyΔE S0-T i1and the spin-orbit coupledS0→T i1transition dipole moment（M iα）：

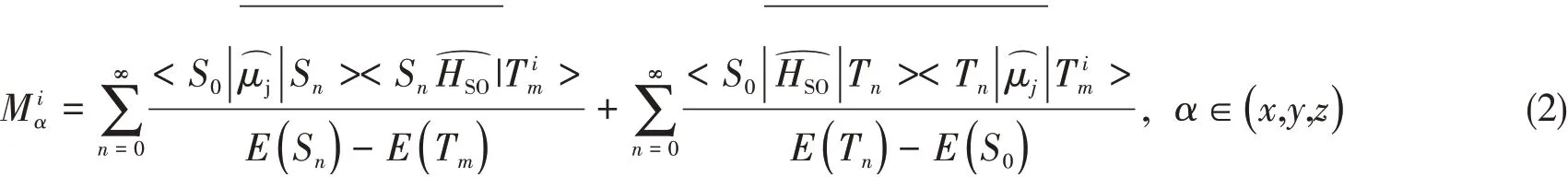
which is calculated by including spin-orbit coupling perturbatively in Amsterdam Density Functional package（ADF 2016）［25］.An all-electron TZP basis set applied for Pt，while DZP was selected for all other atoms.No core electrons were frozen during the SCF calculation.The B1LYP hybrid exchange-correlation functional with HF value 0.3 is selected to perform the DFT calculations.With the already convergedT1geometry from G16，under one-component zero order regular approximation（ZORA）［26］，perturbative spin-orbit coupling（pSOC）［27］calculation including at least 10 lowest scalar relativistic singlet and triplet excitations is performed to obtain the spin-orbit coupling matrix elements，emission energy and the associated radiative decay rate.The following technical configurations were employed：Becke numerical integration grids of“Good”quality，Exact Density，SCF converge tolerance 1×10-6，gradients convergence of 1×10-5for geometry optimization.The experimental electronic properties are dependent upon the environment.Therefore，we included salvation effects by implicitly modeling solvent CH2Cl2according to the conductor-like screening model（COSMO）［28］.For pSOC TDDFT calculations，the effect of the excitations on the COSMO surface charges of the excitations were not taken into account.

Note that individual phosphorescence rates for the three spin sub-states can only be observed experimentally in the limit of large fine-structure splitting and at low temperatures.In the higher temperature limit，spin relaxation is usually fast and the triplet levels are almost equally populated，and only the weighted phosphorescence rates can be measured.Therefore，phosphorescence rates are calculated according to

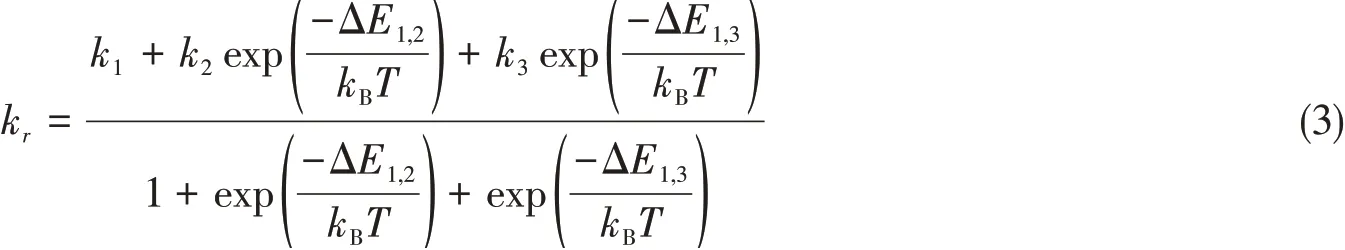
In current contribution，the final data are corrected for the refractive indexn（n=1.4241 for CH2Cl2）according to the Strickler-Berg relationship［29］.

Each individual inter-system crossing（ISC）channel is treated as a non-radiative transition betweenSnandTmexpressed by Fermi Golden rule［30，31］，

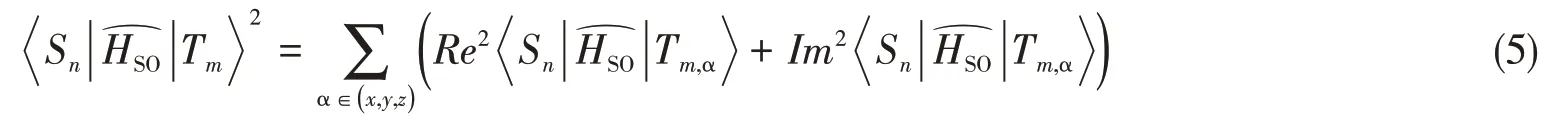
ρFCis the Franck-Condon weighted density of states，which can be evaluated in the framework of Marcus-Levich-Jortner theory：

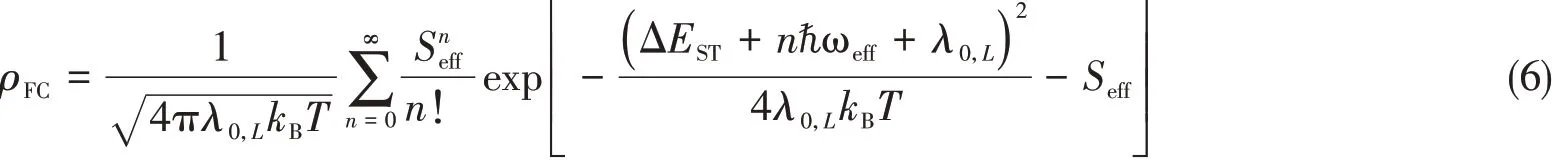
Here，λ0，Lis the Marcus reorganization energy associated with geometric relaxation energy（λ0）and intramolecular low-frequency vibrations（λL）；kB，the Boltzmann constant；T，temperature；ℏωeff，the effective energy of a non-classic vibrational mode involved in the transition；andSeffis the corresponding Huang-Rhys factor.In Marcus-Levich-Jortner model，in order to simplify the calculations of the Franck-Condon-weighted density of state，the effect of all contributing modes is approximatedviaan effective mode with an effective frequency，ωeffand effective Huang-Rhys factor，Seff，as defined bellow：

where the summation only runs over the interested high-frequency vibrations modes.A vibrational mode is determined to be a low-frequency one if its energy is smaller than 1000 cm-1，or a high-frequency one if 1000 cm-1≤ℏω＜1800 cm-1，as suggested by Tonget al.［32］for transition metal complex within two-mode approximation.For transition from singlet stateS nto triplet excited stateT m，intersystem crossing rateand the reverse intersystem crossing ratecan evaluated by the above equations.In current contribution，all higher energy singlet excited state geometries are approximated byS0geometry，similarly，all higher triplet excited state geometries are approximated byT1geometry.Therefore，the geometrical relaxation energy caused by intersystem crossing and reverse intersystem crossing is ignored andλ0，Lis simplified asλ0，L=λL，only contributed by lower-frequency vibrational normal modes.The low-frequency vibration relaxation energy and the associated Huang-Rhys factor were calculated by using the DUSHIN code developed by Reimers［33］.

Classifying all vibration modes into three active modes，one of low frequency（ωs＜1000 cm-1），a second of intermediate frequency（1000 cm-1≤ω0＜1800 cm-1），and a third of high frequency（ωf≥1800 cm-1），under threemode approximation，the non-radiative decay rate fromcan be written as

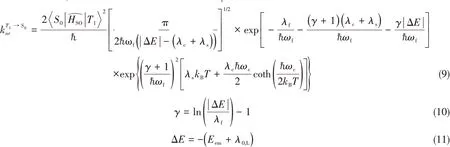
Where，Eemis the emission energy.λ0，Lis the reorganization energy contributed by low-frequency vibrational modes（λs）and geometric relaxation energy（λ0）caused by the change of electronic states fromT1toS0.

2 Results and Discussion

2.1 Molecular Geometric and Electronic Property

The coordination center around Pt metal exhibits a planar geometry.For tetra-Pt-1，tetraPt-2，and tetra-Pt-3，the phenol ligand and PtˆOˆNˆCˆN center are not co-planar，in fact a slight upward tilt，as shown in Fig.2.The interaction between metal and ligand is sensitive to the change of charge population on PtˆOˆNˆCˆN framework.Though the highest occupied molecular orbital（HOMO）is mainly delocalized on the two adjacent benzene rings along the O—Pt—C direction，removing the electron donating groups tert-butyl and 3，5-di-tertbutyl-phenyl out of the PtˆOˆNˆCˆN framework leads to the electronic rearrangement，which causes the change of metal-ligand interaction，evidenced by change of Pt—C and Pt—O bond length as reported in Table 1.For tetra-Pt-2 and tetra-Pt-3，there’s no electron donating modification to phenol group.Therefore，almost similar Pt—C bond length，but both a bit longer than Pt—C bond length in tetra-Pt-1.From tetra-Pt-1 to tetra-Pt-3，the interaction between Pt and phenol ligand is strengthened.And this interaction is further enhanced in tetra-Pt-3 when promoted into the triplet exited state geometry（Pt—O，0.20587vs.0.20447 nm）.

Fig.2 Optimized ground state geometry,PBE0/LanL2TZ(f);6-311G(d,p)level of theory

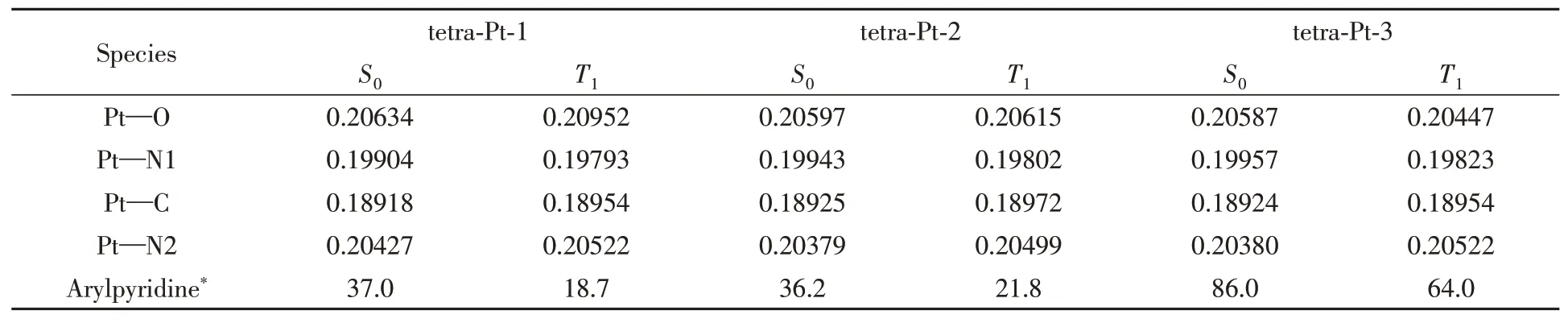
Table 1 Metal bond length(nm)and dihedral angles(°)between aromatic groups and ligand in ground state and the lowest triplet excited state

The subtle differences reflected in the ground state structure are amplified in the excited state structure，resulting in a significant conformational change，leading to remarkable differences in the observed emission color and efficiency.With the optimized triplet structure，the emission maximum was well reproduced by ADF2016，as reported in Table 2.TD-DFT calculation reveals the observed emission is mainly contributed by electronic transition between HOMO and the lowest unoccupied molecular orbital（LUMO）.As illustrated in Fig.3，the HOMO mainly populates on phenol ligand，and with little contribution from metal as well as phenyl ligand.Nevertheless，the LUMO in triplet excited state is delocalized on both pyridine fragments，and phenyl fragment，even extends to 3，5-di-tert-butyl-phenyl electron donating group in tetra-Pt-1 and tetra-Pt-2，but not that much in 2，6-di-methly-phenyl fragment in tetra-Pt-3，since the two methyl groups hold phenyl vertically to pyridine，which therefore reduces the orbital overlap between the two planes obviously.Based on the above HOMO and LUMO characteristics，the observed emission is assigned as3LLCT with litter metal participation.The energy levels of low-lying singlet excited state can be effectively tuned by modifying theσbonded phenol ligand.In tetra-Pt-3，no modification to phenol，but the 2，6-di-methlyphenyl group constrains the charges populated on the backbone of PtˆOˆNˆCˆN，which stabilizes theS1andS2states，resulting in the degeneratedS1andS2states.While in tetra-Pt-2，this constrain is less active since the reduced dihedral angle between 3，5-di-tert-butyl-phenyl and pyridine，indicating more stronger orbital overlap，giving out a smaller energy barrier betweenT2andT1，as compared with the energy barrier betweenT2andT1in tetra-Pt-3.Whenstrong electron donating group tert-butyl group is introduced to phenol，low-lying singlet state was destabilized，evidenced by the relatively largerS1andS2energy barrier in tetra-Pt-1，as shown in Fig.4.

Table 2 Calculated emission values(E em),radiative and non-radiative decay rate constants from T1 to S0 state(1×104 s-1),together with available experimental values[34,35]

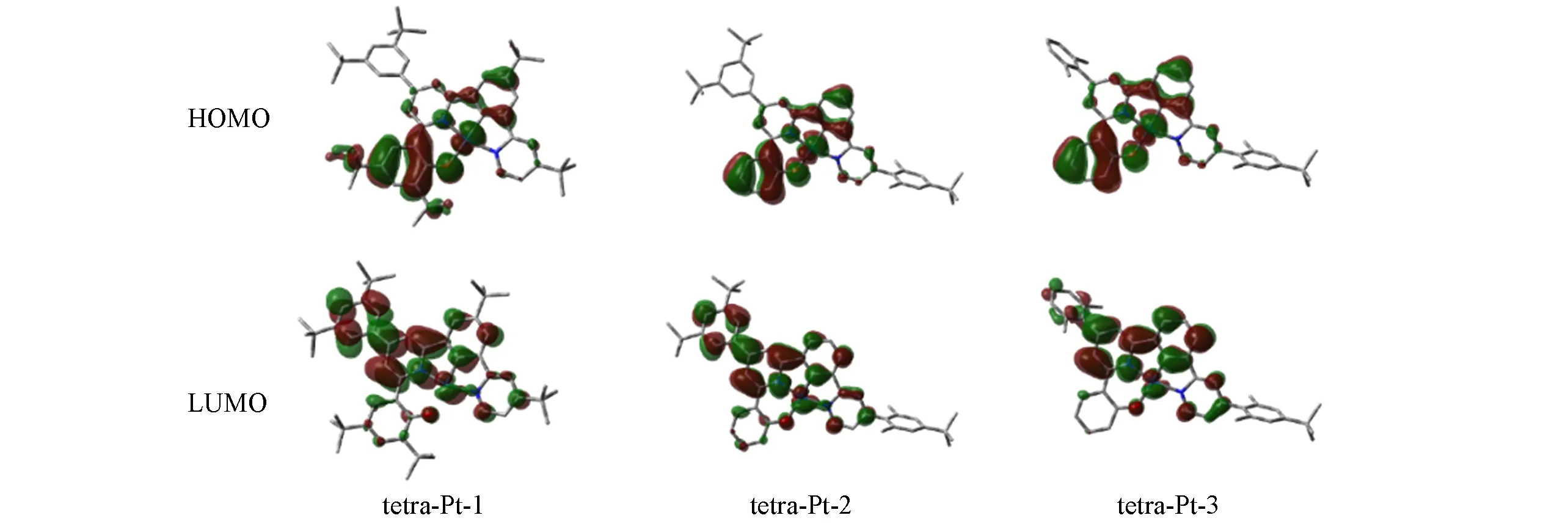
Fig.3 Molecular orbitals contributing to the observed emission

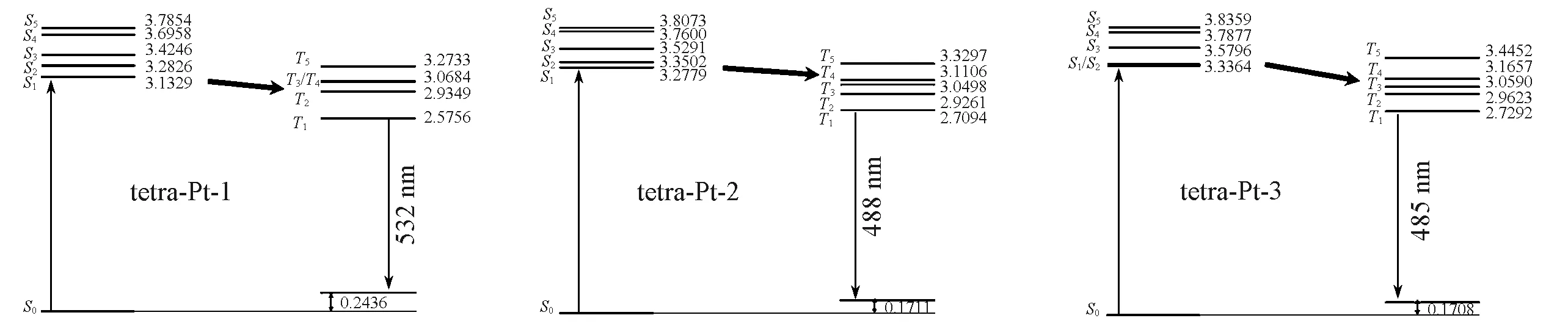
Fig.4 Excited state energy(eV)levels

2.2 Emission Characteristics

With the calculated radiative and non-radiative decay rate constant，tetra-Pt-2 and tetra-Pt-3 are expected to be highly emissive in green and light blue color，respectively.Both the emission energy and rate constant agree well with the experimental values.The comparable emission efficiencies for tetra-Pt-2 and tetra-Pt-3 can be explained by their similar electronic structure.In chemical formula，the only difference is to replace 3，5-di-tert-butyl-phenyl group in tetra-Pt-2 with 2，6-di-methyl-phenyl group to configure tetra-Pt-3.Both 3，5-ditert-butyl-phenyl and 2，6-di-methyl-phenyl are electron donating groups，together with 2，6-dimethly-4-tert-butyl-phenyl group，they act like a charge firewall，holding the excited charges within PtˆOˆNˆCˆN framework.Because 3，5-di-tert-butyl-phenyl group is not perpendicular to PtˆOˆNˆCˆN plane，the charge firewall is not that strict in tetra-Pt-2 as compared with tetra-Pt-3，thus part of the excited charges may escape from the PtˆOˆNˆCˆN center and diffuse to the 3，5-di-tert-butyl-phenyl group，relatively reducing the charge density within metal center，finally giving out the slightly lower excited state energy levels as compared with tetra-Pt-3.Putting all the above together，it can be easily speculated that tetra-Pt-3 will be emissive in higher energy due to its relatively higher excited state energy levels，which is consistent with TD-DFT calculation and experimental values.

Though distinguishable in emission character，tetra-Pt-1 and tetra-Pt-2 are quite different in excited state energy levels and emission color.With four tert-butyl electron donating groups attached OˆNˆCˆN scaffold in tetra-Pt-1，charge density is greatly enhanced on PtˆOˆNˆCˆN center as compared with tetra-Pt-2.There is only one possible vulnerability on the charge firewall，that is the possible charge conjugation between 3，5-di-tertbutyl-phenyl group and pyridine ligand.On the one hand，the difference in the dihedral angle between the ground state and the excited state shows that the 3，5-di-tert-butyl-phenyl group and pyridine ligand tend to be coplanar in the excited state，which greatly enhances the conjugation between the two and further relaxes the limitations of the charge firewall，so that in the excited state more charges diffuse through this pathway to the 3，5-di-tert-butyl-phenyl group，and finally the charge density on the PtˆOˆNˆCˆN center is significantly reduced.In other words，this kind of electronic configuration gives out a more discrete wave function in triplet excited state，resulting in a bit smaller wave function overlap in tetra-Pt-1 as compared with tetra-Pt-2.On the other hand，without the extra tert-butyl groups，charge density is a bit lower in tetra-Pt-2，the dihedral angle between 3，5-di-tert-butyl-phenyl group and pyridine ligand is a bit larger（21.8°vs.18.7°，see Table 1），indicating a less conjugation between 3，5-di-tert-butyl-phenyl group and pyridine ligand.Therefore，the excited charges are more localized within PtˆOˆNˆCˆN center，as compared with tetra-Pt-3，which intensifies the wave function overlap，therefore gives out the larger energy gap between singlet and triplet state.As illustrated in Fig.4，the average energy gap between singlet and triplet excited state tetra-Pt-2 is a bit larger than in tetra-Pt-1.

2.3 Intersystem Crossing(ISC)Channels

Phosphorescence is based on fast intersystem crossing（ISC）from singlet to triplet excited state and relatively slower reverse intersystem crossing（RISC）channel.The Franck-Condon weighted density of states is actually a Gaussian type function，therefore，in the case where the SOCME values are comparable with each other，the magnitude of the singlet and triplet energy split determines the final rate constant.All possible ISC channels and the corresponding rate constants are tabulated in Table S1（see the Supporting Information of this paper）.For tetra-Pt-1，the fastest ISC channel isS1→T2，withkISC=2.74×1011s-1.The most possible decay pathway would be the following，starts from high-lying singlet excited state，decays to the lowest-lying singlet excited stateS1viainternal conversion，which would be ultrafast，then converts to triplet excited stateT2viaspin flip，after another internal conversion，decays toT1，finally emits out a photon and relaxes to ground state.It should be noted that large energy gap exists in triplet excited states（ΔET2-T1=0.36 eV）betweenT2andT1，which may slow down the internal conversion and provide extra opportunity for other nonradiative decay channel.This may be the reason why tetra-Pt-1 has the relatively largeknrvalue and smallerkrvalue.

For tetra-Pt-2，due to the comparableΔESTvalues，SOCME values are the only factor that really determines the rate constants.With the largest SOCME value（Table S1），S1→S4is calculated to be the fastest ISC channel.For tetra-Pt-3，the fastest ISC channel happens betweenS1andT3.Both internal conversion pathways cover a little energy barrier，0.22 eV in tetra-Pt-2vs.0.23 eV in tetra-Pt-3，which are both smaller than the energy gap in tetra-Pt-1 and Pt-3，therefore smallerknrvalues.

Based on the above analysis possible ISC channel and decay pathways，it is the lowest3LLCT excited state that contributes to the observed emission，not3MLCT，indicating even if with little participation of metal content，highly emissive excited state is possible.

2.4 Non-radiative Decay

Table 2 presents the radiative and non-radiative decay rate constants calculated for each of the lowest triplet excited states of these tetra-Pt complexes.Although thekrvalues are well reproduced，theknrvalues are only consistent with the experimental values in relative order and magnitude.Theknrvalues for tetra-Pt-2 and tetra-Pt-3 are slightly underestimated by a factor of 10.This deviation may be raised from the approximation that all vibrational normal modes are harmonic oscillators.It goes even worse when high frequency vibration modes provide non-negligible contributions toT1→S0non-radiative decay.

Huang-Rhys factor serves to quantify the structural distortion between the emitting triplet excited state and the ground state.As reported in Table S2（see the Supporting Information of this paper），relatively largeSeffvalues indicate obvious structural distortion are induced by low frequency vibration normal modes.The low frequency vibrational modes can be roughly assigned as Pt—O and Pt—N stretching vibration and C—H rotation from CH3groups.In tetra-Pt-1，three tert-butyl groups are attached to phenol and phenyl ligands，which both interact with metal centerviaσbond and therefore both sensitive to the extra vibration introduced by C—H rotation.If the amplitude of C—H rotation can be lowered，some of the possible non-radiative decay channel could be turned off，resulting a smallerknrand finally a larger overall quantum efficiency，which is consistent with the experimental observation that quantum yield increased when detected in PMMA.For tetra-Pt-2 and tetra-Pt-3，although C—H rotation from CH3groups contributes to low frequency vibration modes，less CH3groups and a bit far away from theσ-bonded sensitive phenol and phenyl ligands，some non-radiative decay channels triggered by C—H low frequency vibrations are no longer present，therefore，knrvalues drops dramatically.It should be noted that without steric hindrance 3，5-di-tert-butyl-phenyl can rotate to new conformation which is co-planar with PtˆOˆNˆCˆN，therefore expands the molecular plane and frees up more space.As a result，it is possible for two tetra-Pt-2 molecules accumulated in the staggered conformation，corresponding to the observed excimer emission for tetra-Pt-2 in 5%PMMA.

3 Conclusions

We have carried out a detailed theoretical study to investigate the structural-photophysical relationships of tetra-Pt emitters.It is generally believed that increasing the rigidity of the ligand in a transition metal complex can minimize structural distortion between the emitting triplet excited state and the ground state，thereby decreasing the non-radiative decay rate.Along the O-Pt-C axis，phenol and phenyl ligands are connected to Pt metal centerviaσbond.Within the N-Pt-N axis，the pyridine ligands are linked with Pt metal centerviacoordination bond.Detailed analysis on molecular orbital and exited state energy levels reveal that the electronic structure and wave function overlap between the emitting excited state and ground state are very sensitive if any modifications present on theσbonded phenol and phenyl ligands.We found that for this particular molecular system，if the ligand modification is carried out along the O-Pt-C axis，the photophysical properties，ISC channel，and non-radiation process will change dramatically.However，the effect of ligand decoration along the N-Pt-C axis is not very obvious.In the O-Pt-C axis direction，the elimination of tert-butyl group，can effectively reduce the low frequency C—H vibration on the ligand，thereby significantly reducing the non-radiation transition process.In addition，the reasonable regulation of the charge density and the charge distribution form on the PtˆOˆNˆCˆN plane can effectively control the nonradiative process.For example，in tetra-Pt-2，with the controllable rotation of tert-butylbenzene group，the wave function overlap between the triplet excited state and the ground state can be effectively controlled，resulting in a high emission efficiency for single molecule（the quantum yield is up to 0.90 in diluted CH2Cl2solution）.In PMMA，due to molecular aggregation 3，5-di-tertbutyl-phenyl group may adapt a new conformation which is more co-planar with PtˆOˆNˆCˆN，the LUMO would be more delocalized，and the charge density lowered thereby，resulting in the sharp drop in quantum efficiency for tetra-Pt-2 in PMMA.In contrast，the electron donating groups in tetra-Pt-3 cannot rotate due to the steric hindrance of methyl groups，therefore the quantum yield is not significantly changed in PMMA.The calculated and experimentalknrvalues are in quantitative agreement.The strong vibration coupling between triplet excited state and ground state in low frequency region is the main channel for non-radiation decay.Our present contribution highlights the importance of the relative order of singlet and triplet excited state and proper control of charge distribution in multi-chromophoric transition metal complexes in designing strongly luminescent transition metal complexes.

The supporting information of this paper see http：//www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20210175.

This paper is supported by the Natural Science Foundation of China（No.21873038）.