轮毂式电机驱动电动汽车主动悬架滑模控制研究*
2021-07-11张云孙劭泽金贤建李韶华杨俊朋王佳栋
张云 1, 孙劭泽 金贤建 † 李韶华 3 杨俊朋 王佳栋
(1.福特汽车工程研究南京有限公司,南京 211100)(2.上海大学机电工程与自动化学院,上海 200072)
(3.石家庄铁道大学机械工程学院,石家庄 050043)
引言
伴随着全球日益复杂的环境问题,轮毂式电机驱动电动汽车作为一种新型能源车辆越来越受到人们青睐.而电动汽车的NVH问题,即噪声、振动及舒适性的改善问题,也成为研发的重点.其中驾乘舒适性和车辆行驶安全性是对车辆性能评判中最为重要的两个性能指标,而悬架系统是车辆底盘的关键部件,不仅对这两个性能起着决定作用,而且还影响汽车动力的发挥[1,2].因此,如何提升悬架性能是目前各国在悬架上的研究方向.
目前国内外学者对主动悬架控制进行了大量的研究,Mantaras等[3]应用基于层次分析法的车辆半主动悬架LQR最优控制方法,实现了车辆评价指标的综合优化、提高了车辆的平顺性及舒适性,但LQR控制鲁棒性较差;Sun等[4]研究了汽车主动悬架的振动问题,提出了一种饱和自适应鲁棒控制策略,并验证了该控制律的有效性;颜文俊等[5]提出非线性半主动悬架系统模糊控制策略,能大幅度地抑制车身加速度和轮胎动载荷,并一定程度地改善悬架动行程.此外,对于主动悬架常用的控制方法还有神经网络控制[6]、鲁棒H∞控制[7]、滑模控制[8]等.然而国内外对于轮毂式电机驱动电动汽车主动悬架研究则相对较少,且考虑问题均不完善.李以农等[9]提出了电磁主动悬架多目标粒子群优化设计方法,以抑制轮毂电机驱动电动汽车的振动负效应问题,但引起车轮动载荷响应恶化;Du等[10]提出了一种考虑簧载质量变化、执行器故障和控制输入约束的轮毂式电机驱动电动汽车主动悬架可靠模糊H∞控制策略,结果证明了该策略的有效性.
本文将建立悬置式轮毂电机电动汽车四分之一主动悬架模型,设计基于电磁作动器的主动悬架滑模控制策略,运用李雅普诺夫判据证明该系统的稳定性,并引入趋近律方法降低滑动模态带来的抖振现象.最后在MATLAB/Simulink环境中与Carism进行联合仿真,验证所设计主动悬架滑模控制系统对车辆驾乘舒适性及平顺性的影响.
1 电动汽车主动悬架系统建模
1.1 两自由度系统模型
本文悬置式轮毂电机优化结构,加入电磁作动器与传感器,可建立电动汽车主动悬架系统的四分之一模型,如图1所示.为了简化计算,可做以下假设:将汽车悬架系统中的如弹簧、减振器、轮胎以及橡胶衬套等非线性弹性部件视为线性元件;忽略轮胎的阻尼性等.

图1 主动悬架四分之一模型Fig.1 Quarter model of activesuspension
在主动悬架系统的四分之一模型中,m1表示簧载质量(车身与负载质量);z1表示车身垂向位移;m2表示非簧载质量(轮胎与悬架质量);z2表示为轮胎的垂向位移;me表示为轮毂电机质量;z3表示为轮毂式电机的垂向位移;ks、ke、kt分别表示悬架、轮毂电机吸振器和轮胎的弹性系数;Cs、Ce分别表示悬架、轮毂电机吸振器的阻尼系数;q表示路面抖动输入;F表示主动控制力.
根据主动悬架系统的四分之一模型,可建立如下系统动态方程:
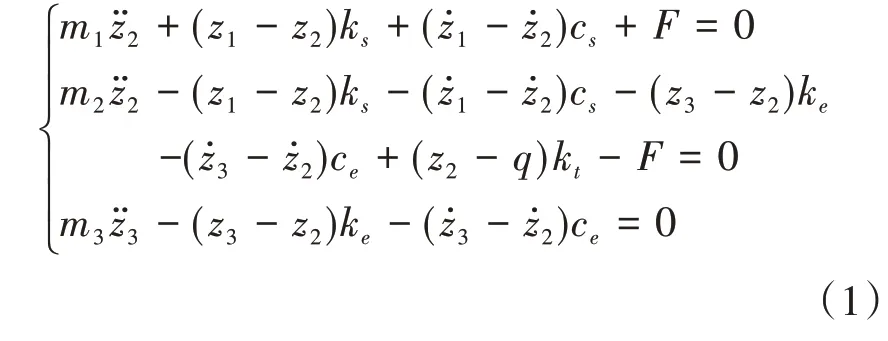
1.2 电磁作动器设计
作动器是车辆主动悬架控制中实现振动主动控制的主要部件,其工作机理图如图2所示.衔铁所受电磁力计算如下:
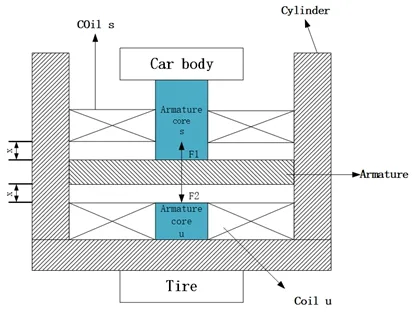
图2 电磁作动器工作基理图Fig.2 Basicprincipleof plectromagnetic actuator
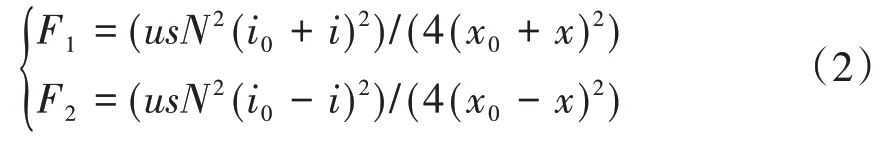
其中,F1,F2分别为作用在衔铁上的向下、向上的电磁力;μ为真空磁导率;s为衔铁表面面积;N为电磁线圈匝数;x0为初始时刻衔铁上表面到电磁线圈a或衔铁下表面到电磁线圈b的距离;x为衔铁移动的距离;i0为初始时刻流经电磁线圈a,b的电流,且为给定常数;i为衔铁受到电磁力作用后流经电磁线圈的电流,并且随衔铁移动距离的变化而变化.
由(2)式可得电磁作动器所受合力为
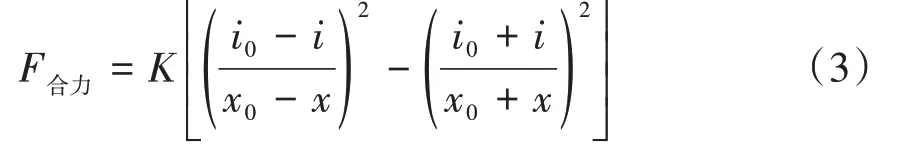
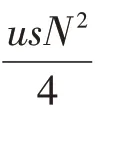
2 滑模控制器设计
2.1 滑模控制定义
对于如下系统

其中,x∈Rn,u∈Rm,t∈R.首先,确定切换函数

然后,求控制函数

若u+(x)≠u-(x),则:
1)滑动模态存在,即式(6)成立;
2)满足前文所提到的可达性条件,即切换面外全部系统点将短时间内运动到滑模区;
3)控制器稳定可靠[8].
2.2 滑模控制器设计
由于系统运动到滑模面时运动点未处于静止状态,惯性的作用使其穿越切换面形成抖振.实际系统中受到一些因素的影响,系统会在滑模切换面上、下做高频抖振,形成锯齿态运动轨迹,这不仅影响控制精度,还可能引起系统震荡及失稳,破坏系统性能,所以,应首先解决降低抖振的问题.本文采用趋近律方法解决抖振问题,指数趋近律形式如下

通过调整趋近律参数κ、ξ,可以保证滑动模品质,并且减弱抖振现象.调整参数中,ξ值取很小、κ值取相对大,大的κ值保证趋近速度在远离滑模面较快,能在很短的时间达到滑模面;而小的ξ值保证了在滑模面附近时趋近速度小,有利于削弱抖振.由式(1)定义如下坐标变换量

将式(3)带入,可得系统动力学模型为

对于切换函数,一般选取如下
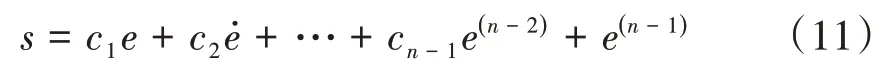
其中,e表示参考值与实际反馈值之间的误差,即跟踪误差;参数ci(i=1,2,…,n-1)需满足Hurwitz多项式c1+c2p+…+cn-1p(n-2)+p(n-1),且参数ci值影响系统的运动点向切换面运动的趋近速度.本文选取控制切换函数为

且

其中,yd为理想悬架动挠度.将式(9)、式(10)代入得

由式(12)得

其中,

则由式(9)、式(14)、式(15)和式(16)得
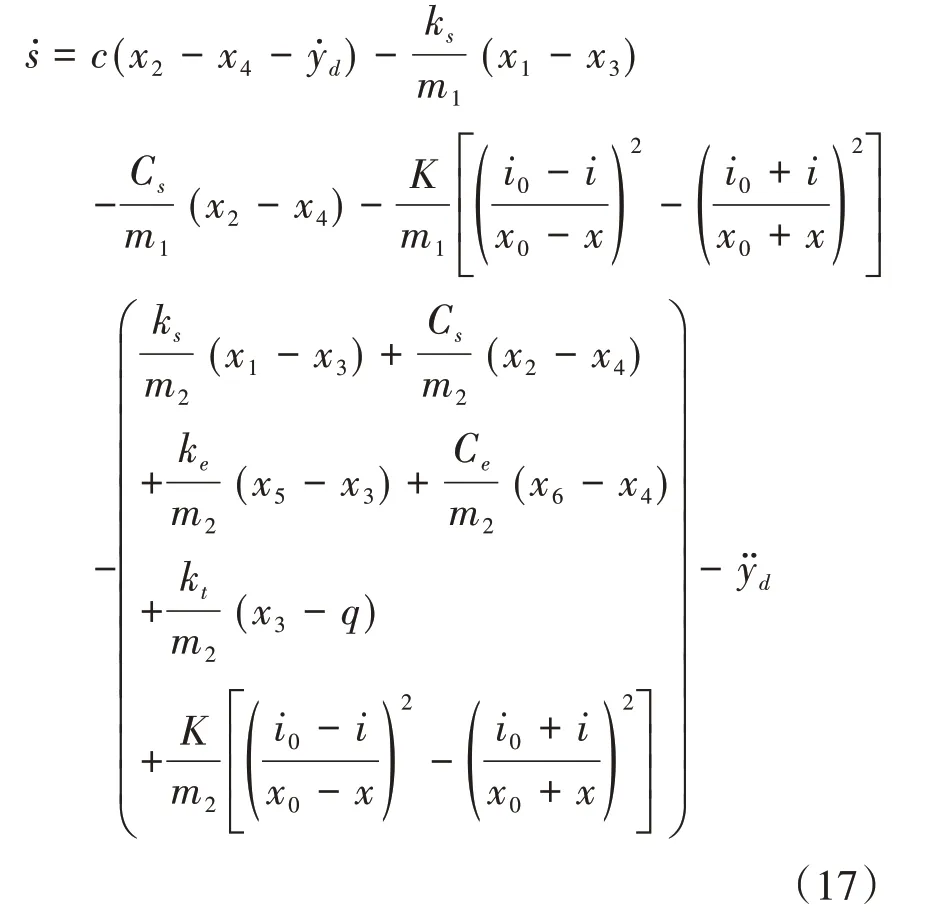
令ṡ=0,可得
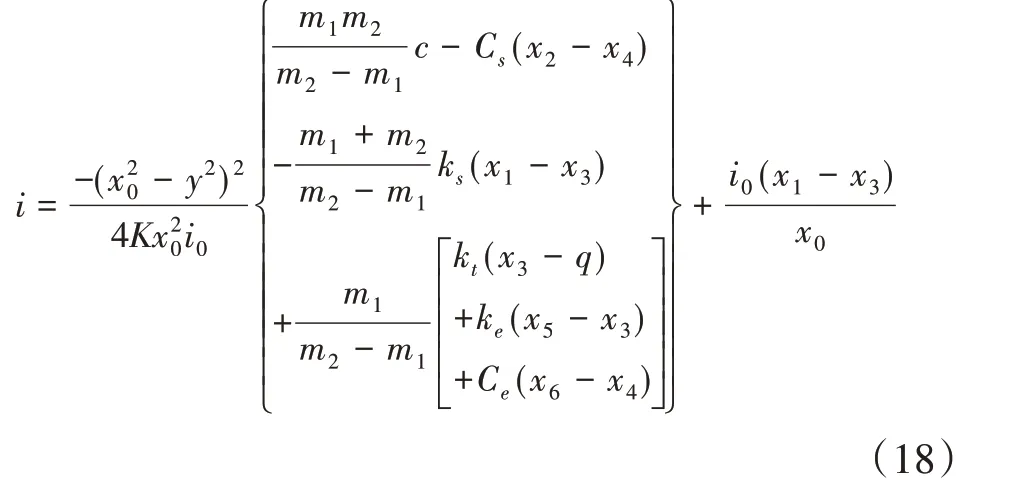
即等效控制项:

一般地讲,滑模控制器中,控制律由等效控制项ieq和切换控制项isw组成,其中,切换控制项可保证系统鲁棒性,抖振也由其导致,即

可设计切换项为
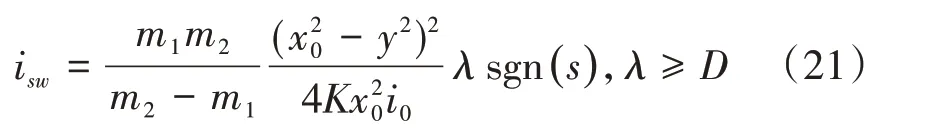
将式(18)-式(21)代入式(17),整理得
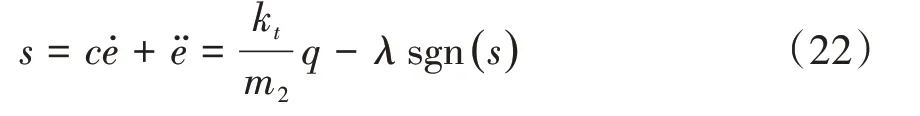

该主动悬架系统滑模控制器的稳定性由李雅普诺夫稳定性判据第二定理判断,即:设李雅普诺夫函数V(x)正定,如果V(x)负定,则控制系统的平衡状态为渐进稳定,本文中取李雅普诺夫正定函数V(x)为:

对上式求导得

将式(23)带入上式得
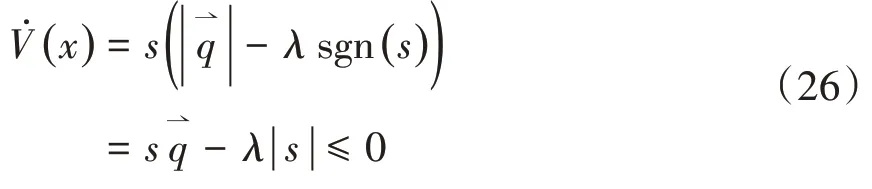
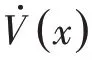
3 仿真与分析
为验证所设计的主动悬架控制器的有效性,在Matlab/Simulink环境中搭建悬置轮毂式电机驱动的电动汽车四分之一主动悬架模型,与Carsim进行联合仿真分析.
3.1 B级路面仿真
在仿真测试中,通过白噪声进行模拟的随机路面输入,限制白噪声的幅值范围对不同路面进行仿真.生活中常见的路况接近于B级路面,可由道路模型生成得如图3所示的随机B级路面.同时,通过将滑模控制器的输出设置为零,该悬架系统可以等效于被动悬架模型,再与滑模控制器正常工作时的主动悬架进行仿真对比.
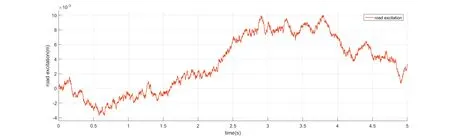
图3 随机B级道路路面激励Fig.3 Random class B road pavement excitation
仿真测试中,悬架动挠度yd在仿真过程中设计为零,滑模控制器的相关参数经调整测试取值为:κ=150,ξ=8,c=10,λ=2.车速设置为20m/s,仿真步长为1ms,仿真时间为5s.
被动悬架与主动悬架系统仿真测试结果对比如图4-6所示,图4-6分别为车身垂向加速度、悬架动挠度和轮胎动挠度.结果表明所设计主动悬架控制系统的效果显著,在受到路面较大振动时,可以尽可能减少车身所受影响,使车轮尽可能与地面接触,保证动力输出,同时确保驾乘舒适性.
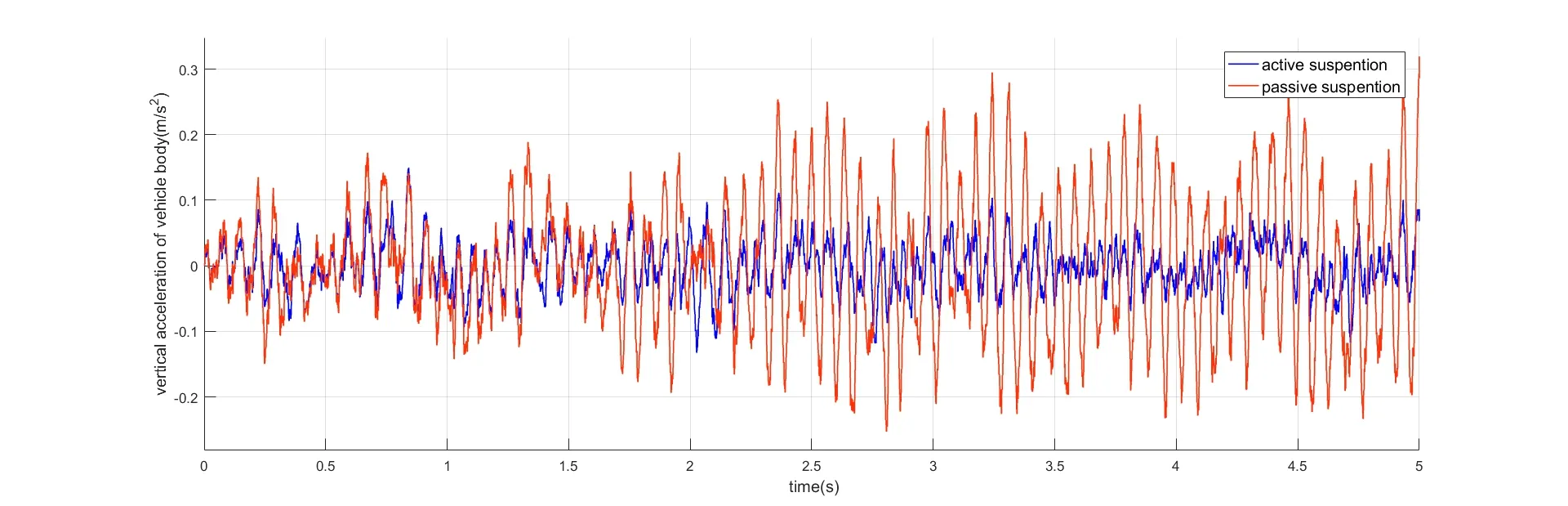
图4 车身垂向加速度对比Fig.4 Thecomparison of vertical acceleration of vehiclebody
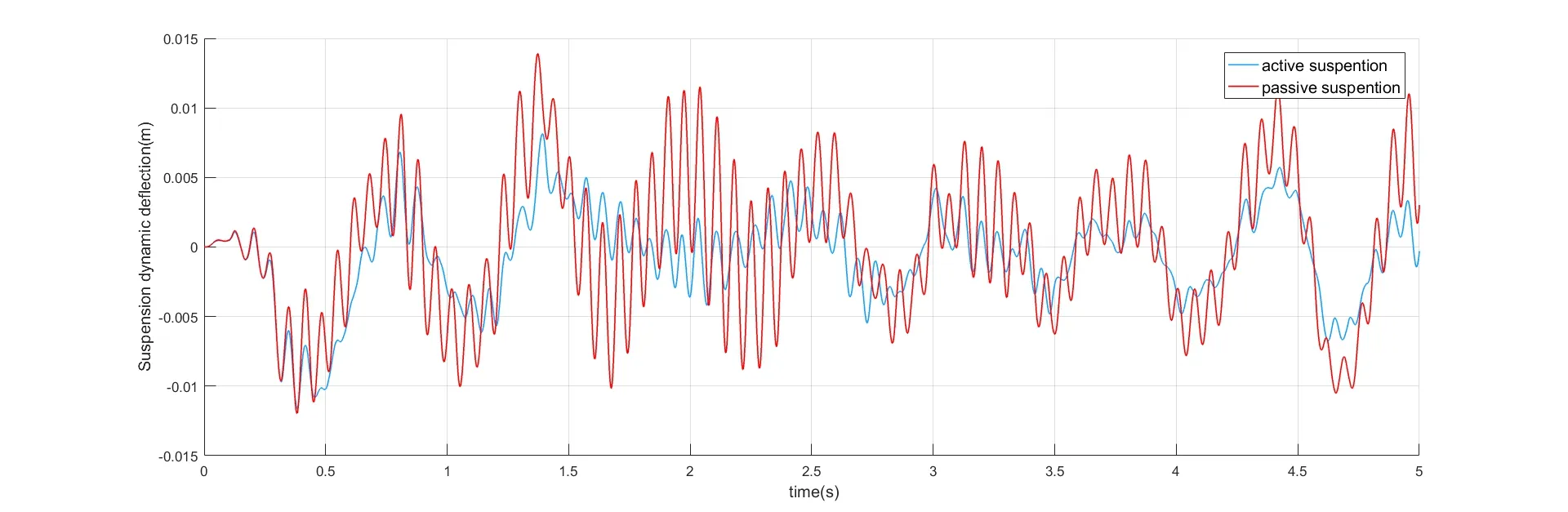
图5 悬架动挠度对比Fig.5 Thecomparison of dynamic deflection of suspension
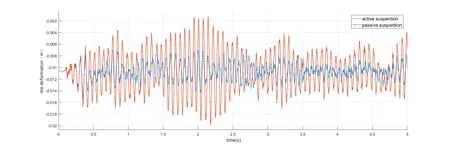
图6 轮胎动挠度对比Fig.6 Thecomparison of dynamic deflection of tiresactuator
3.2 冲击激励仿真
为进一步验证所设计主动悬架系统的有效性与功能性,还进行了冲击激励的仿真测试,冲击仿真可更加直观体现主动悬架的悬架性能.冲击激励模型产生的冲击信号如图7所示.仿真结果如图8-图10所示.图8-图10分别为车身垂向加速度、悬架动挠度和轮胎动挠度.结果表明,在冲击激励仿真中,所设计主动悬架系统也表现出相当优异的悬架性能,并且由于滑模控制器的趋近效果,可以在更短的时间内将抖振现象消除.
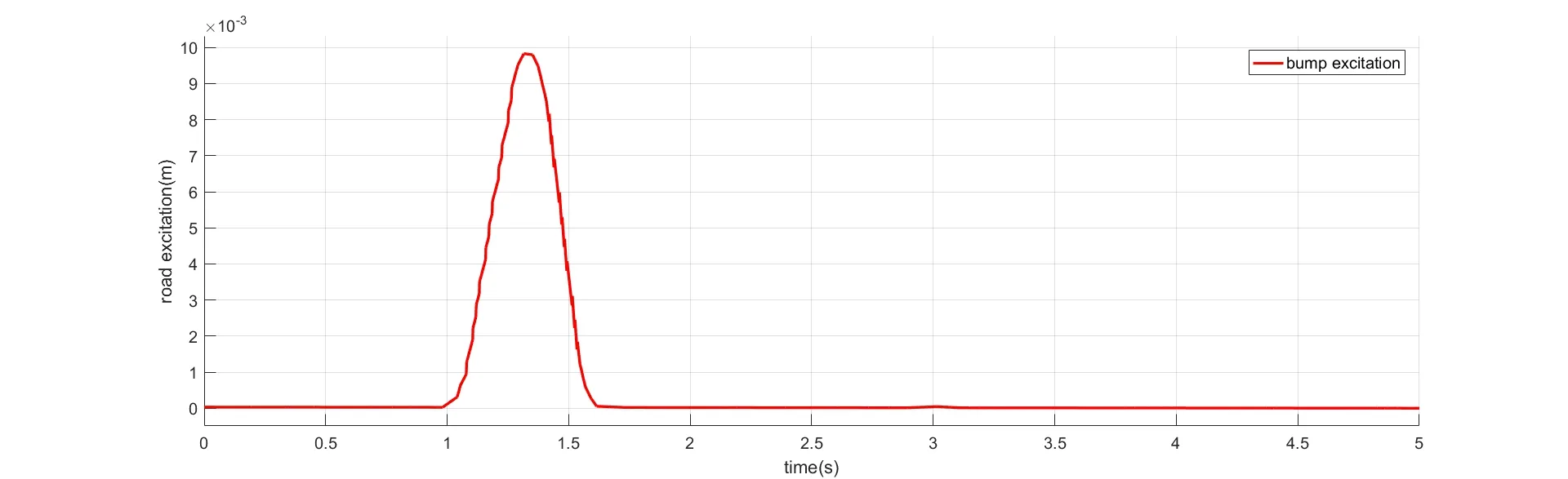
图7 冲击信号激励Fig.7 Shock signal excitation
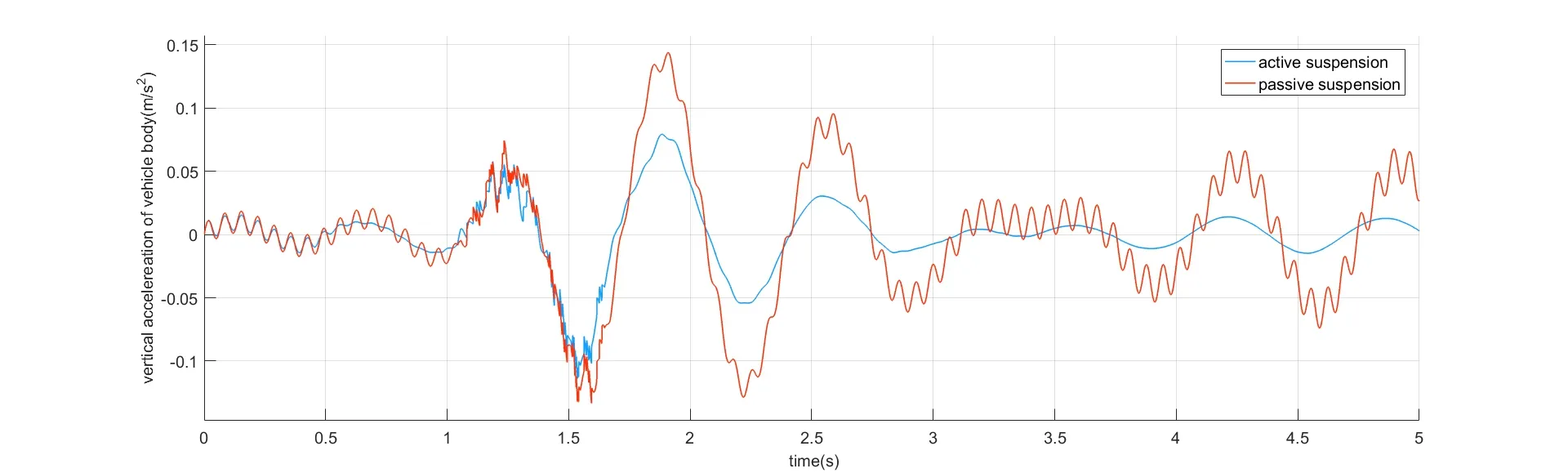
图8 冲击激励下车身垂向加速度对比Fig.8 The comparison of vertical acceleration of vehicle body pact excitation
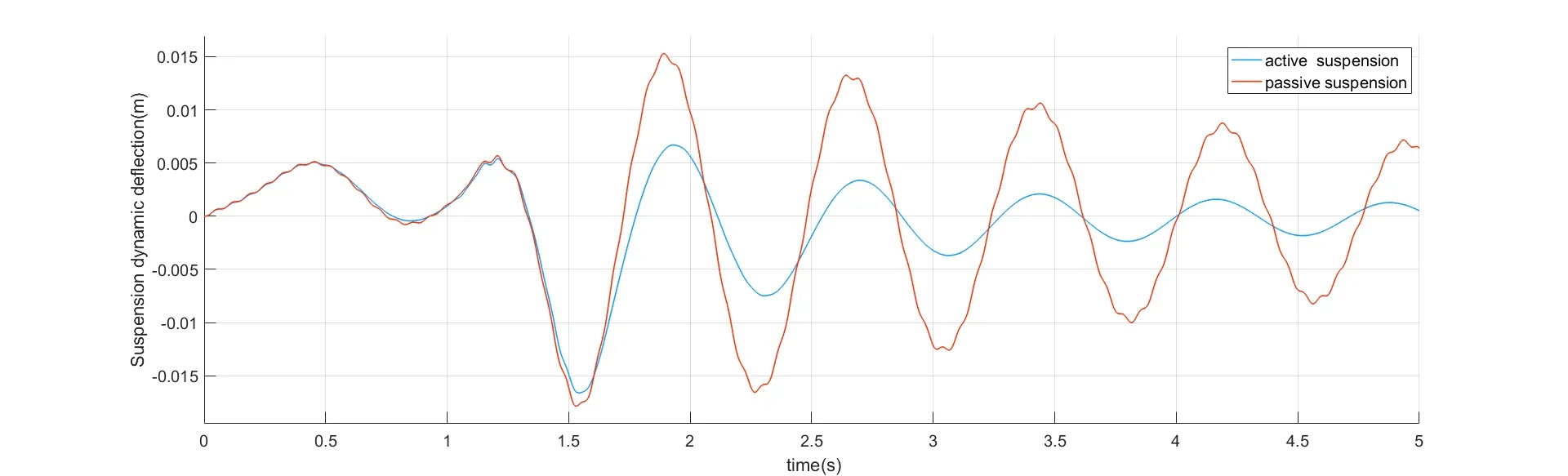
图9 冲击激励悬架动挠度对比Fig.9 Thecomparison of dynamic deflection of suspension

图10 冲击激励下轮胎动挠度对比Fig.10 Thecomparison of dynamic deflection of tiresunder impact excitation
4 结论
(1)为了改善轮毂式电机驱动电动汽车主动悬架性能,建立了轮毂式电机驱动电动汽车四分之一主动悬架模型,为以后进行电动汽车主动悬架分析提供了部分系统模型基础.
(2)根据所建立的模型,设计了基于电磁作动器的主动悬架滑模控制系统,运用李雅普诺夫判据,证明了该系统的稳定性,并采用趋近律方法,降低滑动模态带来的抖振影响.
(3)进行了Matlab/Simulink与Carsim联合仿真,分别在以白噪声模拟的B级路面与冲击激励下验证了所设计主动悬架滑模控制系统的有效性和可行性,表明了该系统能够在保证性能的前提下改善车辆安全性、驾乘舒适性、操作稳定性等.
(4)本文只是设计基于轮毂电机驱动电动汽车主动悬架的滑动模态控制方法,在后续研究中,我们将对轮毂电机偏心与路面机理的耦合进行分析,以及对相应的先进控制方法展开深入研究.
