汽车质量与道路坡度串行估计方法*

2021-07-11张华达林棻赵又群蔡亦璋

动力学与控制学报 2021年3期

张华达林棻赵又群蔡亦璋

（南京航空航天大学能源与动力学院，南京 210016）

随着汽车电子控制技术的飞速发展，车辆状态参数的实时获取越来越受到研究学者的重视.汽车质量和道路坡度是车辆控制系统中的重要参数.汽车质量是基于模型的控制器设计的根本参数，汽车的满载、空载、以及乘员状态都对汽车质量产生影响，因此车辆质量的辨识尤为重要；另外，如果路面坡度已知，那么驱动控制系统可以实时根据坡度信息调整动力系统的输出，提高车辆的能效.

汽车质量直接关系到轮胎垂向力，同时影响横向和纵向轮胎力.文献［1］基于电动四驱车辆提出了一种车辆质量与质心位置的估计算法.该算法包括车轮角加速度、轮胎的垂向力、有效载荷估计器，并由卡尔曼滤波和带有变量遗忘因子的递归最小二乘法进行参数辨识.文献［2］基于两个串行的递推最小二乘法，以汽车出厂初始参数为串行RLS辨识算法的初始值，结合蛇行试验辨识质心位置.而后，将辨识所得的质心位置结合双移线试验辨识得到整车质量.文献［3］则基于六自由度车辆模型，提出了两种RLS算法用于含有道路坡度信息的质量估计.文献［4］证明了在无法得到道路坡度的条件下辨识所得的质量并不可靠，将与真实值出现较大的误差.在汽车质量和道路坡度实时信息同时已知的情况下，汽车在过陡坡时的驱动性能和制动性能将得到极大提升［5］.因此，汽车质量和道路坡度的实时信息对汽车的安全性和稳定性控制以及经济性十分重要.

本文提出一种具有双层结构的参数估计系统.在第一层中，车辆质量是缓慢变化或定常的参数，因此将车辆质量作为系统参数用最小二乘法估计，而不需要使用复杂结构；在第二层中，假设汽车质量已经从第一层得到，再应用基于全局收敛的牛顿迭代法估计快速变化的道路坡度.由于将参数估计分为两层，只有快速变化的参数即道路坡度，需要在每段时间中进行估计，而缓慢变化的参数在不变时可以被认为是恒定的已知值，计算效率得到了提高，减少了计算时间.

1 汽车动力学模型

本文只对车辆纵向运动进行研究，因此本文中汽车动力学研究模型为车辆纵向动力学模型.汽车在实际道路上行驶时，滚动阻力和空气阻力随着环境的改变不断变化，大大增加了汽车纵向动力学模型建立的难度，同时由于它们的影响较小，所以这里忽略滚动阻力和空气阻力对汽车的影响.模型如图1所示.汽车加速时，若行驶道路的坡度为θ，则车辆纵向动力学模型的表达式如下［6］：

图1 车辆纵向动力学模型Fig.1 Vehiclelongitudinal dynamic model

式中，Fx为总的车轮纵向力，Fxf和Fxr分别为前、后轮的纵向力，Fzf和Fzr分别为前、后轮的垂向载荷，Tf和Tr分别为前、后轮的牵引力或制动力矩，m为汽车质量，vx为汽车纵向速度，ωf和ωr分别为前轮和后轮的角速度，I为车轮转动惯量，R为车轮半径.

2 参数估计算法

本节提出了一种双层自适应参数估计系统结构.第一层估计系统：在已知坡度的平坦路面下，由递推最小二乘法估计缓慢变化的汽车参数，即汽车质量；第二层估计系统：将第一层估计系统的输出量作为输入，通过牛顿迭代法进行快速变化的参数即不平坦道路坡度的实时估计.

2.1 第一层：汽车质量估计

在第一层参数估计系统中，基于RLS算法进行汽车质量估计.由（1）可得：

由于运行在平坦路面上，所以θ较小，且恒定不变，因此sinθ≈θ.式（1）中，除m其他参数均可测得，所以有：

其中，

考虑估计系统的一般式［7］：

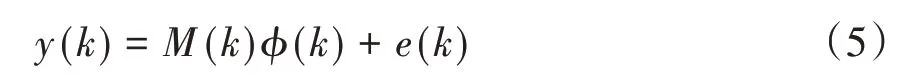
其中，y（k）为系统输出量，M（k）为待辨识的系统参数，φ(k)为输入量，e（k）为噪声.由式（3）与式（4）可得：

其中，L为最小二乘增益，P为误差协方差.为了减少旧数据对对算法的影响，采用带有遗忘因子的递推最小二乘法：

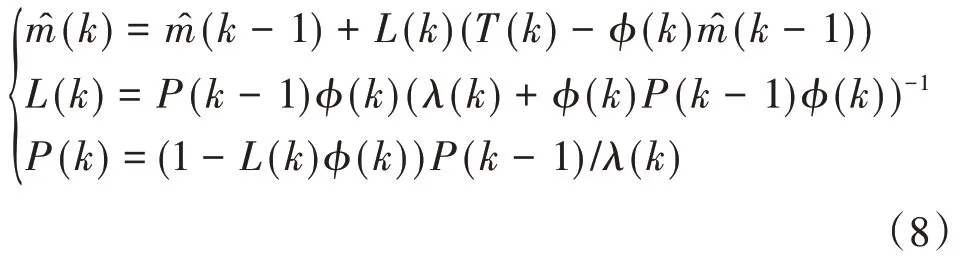
式中，λ(k)为遗忘因子，其取值范围为（0，1］，其取值越小则收敛速度越快，反之则较慢，但结果更接近于真值.本文采用可变遗忘因子［8］：

式中，NINT(ρe(k)2)为接近ρe(k)2的最小整数；ρ为根据试验选取敏感增益，用于确定λ(k)趋于1的取值.

2.2 第二层：道路坡度估计

根据第一层估计系统得出的汽车质量将之代入第二层自适应估计系统来估计道路坡度.考虑具有一般非线性离散时间系统：

其中，θ(t)为时变参数，u(t)为控制输入，y(t)为输出.离散化后得：

由此建立基于牛顿迭代法的参数识别算法：

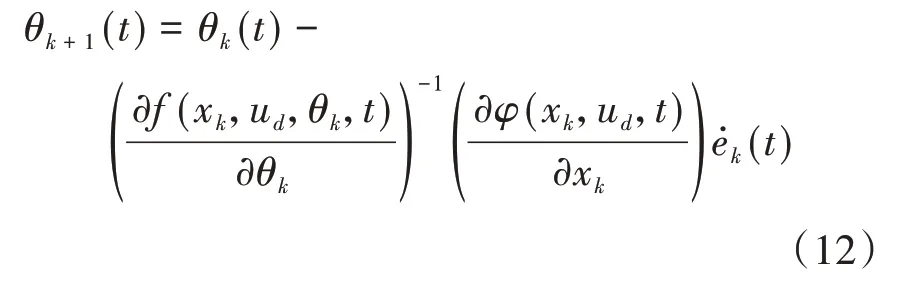
由式（2）与式（10）可得：

定义：

其中μ的取值为［0，1］.因为x(t)与ud(t)满足状态方程，即x(t)为θ(t)与μ的复合函数，所以式（15）可表示为：

通过试验选取适当的迭代次数N，并将［0，1］均分，则有分割点{μi}.

则在第i次迭代中有

其中，

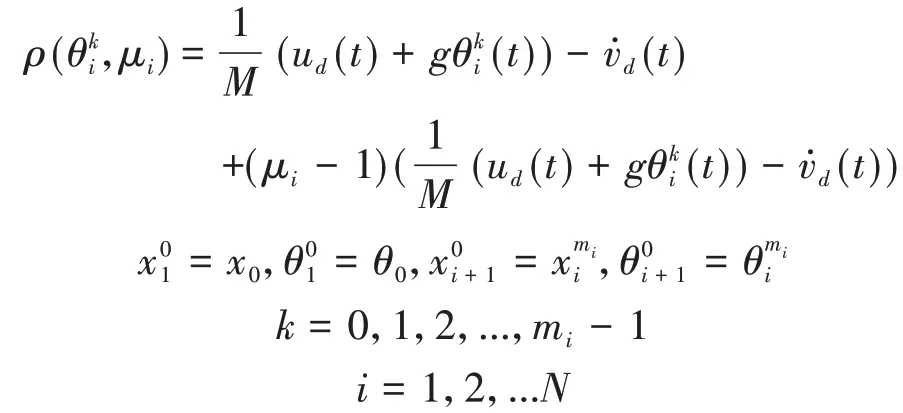
mi为第i次迭代的步数.实际中的车辆纵向速度vx较难测量，由GPS进行测量的方法需要极昂贵的传感器，且在卫星信号受干扰时不可靠.车辆加速度测量存在误差时，加速度的直接耦合将引起较大的抵偿.当本文研究时，由于存在测量噪声与较低的精确度，GPS测速与测量加速度用的惯性力矩传感器（IMU）都不可靠.因此，唯一可靠的测速方案是通过车轮速度测量进行.本文中纵向速度可由车轮角速度计算得出，即vx=ωfR=ωrR（此时假设前后轮角速度一致，且滑移率较小）.

2.3 仿真结果

首先通过数学仿真验证该系统的可靠性，这里使用了Carsim和Simulink联合仿真.本研究中使用一个典型实际车辆进行三组仿真，主要包括整车质量、前轴距、后轴距、车轮半径、车轮转动惯量、质心位置等相关参数，具体参数如表1所示.

表1 仿真车辆相关参数Table1 Parameters of simulation vehicle

在Carsim中设置好实车参数之后，确定控制条件为无转向、无制动（本文只考虑纵向动力学），软件开始仿真出汽车的运动状态，将这一状态传递到simulink中，按照给定算法进行运算，得出估计结果.首先考虑没有测量噪声，这里设置三组仿真，初速度均为5km/h，路面附着系数为0.9：

（1）车辆无负载、道路坡度为零；

（2）车辆搭载200kg负载、道路坡度为零；

（3）道路坡度变化，其余参数与（2）组相同.

结果如图2-图4所示，其中，图2、图3为汽车估计质量与实际质量对比图，图4为道路估计坡度与实际坡度对比图.由图2与图3可知，在（1）和（2）工况下，道路坡度几乎为零，车辆驱动扭矩变化平缓，对缓慢变化的车辆质量估计没有影响.由图2与图3可知，第一层估计系统所估计出的结果在0.4s后开始快速接近于设定值，且较为稳定，并能对汽车质量有较好的估计结果.如图4所示，道路坡度的估计值能够较好地跟踪变化的实际坡度值，说明估计系统的有效性.

图2 第一组仿真结果Fig.2 The results of first set simulation

图3 第二组仿真结果Fig.3 Theresults of second set simulation

图4 第三组仿真结果Fig.4 Theresultsof first set simulation

3 基于模型车平台试验验证

为验证本文所提出的估计系统的有效性与可靠性，通过电控模型车进行试验验证.

3.1 试验平台

本节所用的模型车结构如图5所示，包括电压传感器、电流传感器、加速度计、编码器等测量传感器，可以得到车轮角速度、总驱动扭矩和车辆纵向加速度.这里需要注意的是，模型车的车轮转动惯量较小，所以在试验中忽略该值.具体参数如表2所示.通过编码器测得电机输出轴转速，除以传动比则得到车轮转速，车辆纵向加速度则直接由9轴加速度计陀螺仪模块测出，同时还可以得到模型车与水平面的夹角.总驱动力矩通过下式近似求得

表2 模型车参数Table 2 The parameters of model vehicle

图5 模型车结构Fig.5 Thestructureof model car

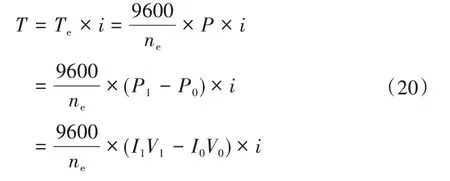
式中，Te为电机输出转矩，ne为电机输出转速，P为电机输出功率，P1为电池在工作状态下的输出功率，P0为电池在待机状态下的输出功率，I1、V1分别为电池在工作状态下两端的电流和电压，I0、V0为电池在待机状态下电池两端的电流和电压.

3.2 模型车质量估计试验

将第一层的估计系统用在模型车上，分别在无负载（3.09kg）和加负载（3.95kg）的条件下进行试验，此时认为坡度值为0.

试验结果如下：

图6、图7为模型车实际质量与估计质量对比图.由图6与图7可以看出，汽车质量的估计值和实际值相差不大，误差始终在一个可接受的范围内.估计值有一些振荡，这是由于加速度测量的噪声所致，通过使用更加准确的加速度计，可以减少测量噪声，使得汽车质量估计值更为精准.

图6 无负载（3.09kg）下质量估计结果Fig.6 Mass estimation resultswith noload（3.09kg）

图7 加负载（3.95kg）下质量估计结果Fig.7 Massestimation resultswith load（3.95kg）

3.3 道路坡度估计试验

在沥青路面上进行第二层的道路坡度估计试验，道路坡度如图8和9所示.试验结果如下所示：

图8、图9为实际道路坡度与估计值对比图.由图8与图9坡度估计结果与实际坡度对比可以看出，坡度的估计值能够较好地跟踪实际坡度值.然而，估计结果中仍然存在一定的扰动.这主要是由于以下几个原因：（1）爬坡时模型车摇摆导致传感器噪声较大，同时，模型车不能很好地满足直线行驶这一条件；（2）当道路坡度发生变化时，转向伺服电机消耗大量电池电力，以保持车辆直线行驶，从而导致功率测量不准.