基于聚类分析算法的锂离子电芯一致性分选

王焰辉,黄志福,林宇星,刘建炜

( 1. 福州理工学院商学院,福建 福州 350506; 2. 华侨大学信息科学与工程学院,福建 厦门 361021;3. 中国人民银行泉州市中心支行,福建 泉州 362000; 4. 福州大学土木工程学院,福建 福州 350108 )

电池组中单体电池的不一致性不仅影响对荷电状态、健康状况等参数的正确判断,而且还会造成电池组容量衰减和寿命缩短,甚至引发安全问题。 已有学者针对电芯一致性分选配组方法展开大量研究。 K.Z.Fang 等[1]结合人工神经网络,基于电池的充电热性能,将电池分选为不同热状态的组别;J.B.Zhang 等[2]采用电化学阻抗谱和等效电路参数筛选电池;Y.Jiang 等[3]基于增量容量分析,提出一种时效机制的筛选策略。 以上研究方法均是基于单体电芯的检测,配组效率较低,无法满足大规模电池一致性分选要求。

在此研究背景下,本文作者基于实验测试所得1 024 只锂离子电池电芯的数据,以STATA、SPSS 和MATLAB 等软件为基础,引入KOHONEN 网络聚类法、广义神经网络回归聚类算法、传统的系统聚类法及模糊C 均值(FCM)聚类法,进行横向对比,研究电芯一致性分选问题,探究更有效的分选配组策略,为实际应用提供判断依据。

1 数据预处理

1.1 数据获取

实验测试用电芯为ICR18650-3200 钴酸锂锂离子电池电芯(江门产),共1 024 只,从00001 编号至01024。 电芯的标称电压为3 700 mV,标称容量为3 200 mAh。

用BAT-NEPDQ-01B-V016 星云锂离子电池组成品测试系统(福州产)进行测试,数据在两种情况下得出。 数据集1是将这批电芯经过系列充放电工序[以0.5C(1 600 mA)恒流充电至4.2 V,转恒压充电至电流为10 mA,简称恒流-恒压充电,以0.5C恒流放电至电压为3.0 V]后,在温度(25±2) ℃、相对湿度65%±20%的环境下,以恒流-恒压充电得出的数据;数据集2 是将这批电芯先恒流-恒压充电后,以0.5C恒流放电60 min 得出的数据。

1.2 筛选不合格电芯

在正式分选配组和组装电池模块前,快速筛选不合格的电芯。 首先,根据目前国内电池厂商对电芯的配组要求筛选不合格电芯,如容量不低于3 000 mAh,电压不低于3.290 V,内阻不高于60 mΩ,温升不高于40 ℃,按标准文件退库。 锂离子电池的质量、性能及使用稳定性虽然取决于电压和内阻,但要达到理想的使用效果和使用时长,关键还是取决于存储容量。 在放电时,电池的电压随电量的减少会逐渐降低,并且有相当大的斜率,因此,通过目前常用的锂离子电池开路电压对容量的关系,进一步筛选不合格电芯,以完成大样本数据下实验数据的预处理。

2 不同聚类算法下电芯快速分选配组

2.1 分选变量的获取

在进行多参数分选前,需要确定分选变量,分选变量应以电池性能一致性的表现形式为依据进行选择。 参考李波等[4]的研究,结合电池参数与电池电芯一致性的关系,最终选取以0.5C恒流放电60 min 时的电压(U)、内阻(R)和温度(t),以及恒流-恒压充电的实际容量(C0)、电压(U0)、电阻(R0)、温度(t0)和压差(ΔU)等8 个指标作为电池的分选变量。

在国内配组要求和目前主流锂离子电池的开路电压和容量标准下,从1 024 只电芯中筛选出950 只作为研究对象,相应的技术参数如表1 所示。

表1 锂离子电池电芯的分选参数 Table 1 Sorting parameters of Li-ion battery cell

2.2 系统聚类法分选电芯

聚类分析是直接比较各事物之间的性质,将性质相近的归为一类,性质差别较大的归入不同类的技术。 围绕聚类分析思想,在使用系统聚类时,要定义两个类之间距离测量和样本之间距离测度的方法。 平方欧式距离(d)应用广泛,可用来作为i个样本间距离的衡量标准,表达式见式(1):

式(1)中:xi和xi+1分别代表两只电池电芯的某个变量。

因为组间连接法的分类效果较好,应用较广,所以选取该方法对电池聚类。 运用SPSS 软件对筛选后的950 只电芯的8 个分选变量作系统聚类,得到图1 所示的谱系图。

图1 950 只电芯数据的谱系图Fig.1 Spectrum of the data of 950 cells

对图1 进行分析,基于横断法观察分类个数(通常使用一条线截断分类线来获得分类结果),为达到同类电芯参数一致的目的,需保证尽可能短的类间距离,因此图中虚线(即为横断截线)把谱系图直观地分成了4 个大类,即横断线切割过的4 条直线所对应的聚类集合电芯样本。

2.3 模糊C 均值(FCM)聚类分选电芯

FCM 聚类算法是用隶属度确定每个元素属于某个类别程度的一种聚类算法。 FCM 算法把n个数据向量x分为c个模糊类,并求得每类的聚类中心,使模糊目标函数最小。模糊聚类目标函数为:

式(2)中:uij为个体xi属于第j类的模糊隶属度;m为模糊权重指数;vj为第j类的聚类中心。

uij和vj的计算公式为:

FCM 聚类算法迭代过程如下:

①给定类别数c、模糊权重指数m;

②初始聚类中心v;

③根据式(3)计算模糊隶属度矩阵u;

④根据式(4)计算每类中心v;

⑤根据式(2)计算模糊聚类目标值,判断是否满足结束条件,满足则算法终止,否则返回步骤③。

FCM 算法最终得到了模糊隶属度矩阵u,个体根据隶属度矩阵每列最大元素位置,判断个体所属类别。 系统聚类法根据电芯一致性原则将电芯分为4 类;在FCM 算法中,同样将电芯分选配组为4 类。

2.4 基于KOHONEN 网络的聚类算法

KOHONEN 网络是自组织竞争型神经网络的一种,该网络为无监督学习网络,能够识别环境或产品特征并自动聚类。

使用MATLAB 软件进行KOHONEN 网络训练的步骤可分为以下5 步。

①网络初始化。 初始化网络权值w。

②距离计算。 计算输入向量X=(x1,x2,…,xn)与竞争层神经元j之间的距离dj。

③神经元选择。 把与输入向量X距离最小的竞争层神经元g作为最优匹配输出神经元。

④权值调整。 调整节点g和在领域Ng(t)内包含的节点权系数,即:

式(6)-(7)中:pg、pt分别为神经元g和t的位置;norm计算两个神经元之间的欧几里得距离;find 为查询非零位置的索引函数;r为领域半径;η为学习速率。r、η一般随进化次数的增加而线性下降。

⑤判断算法是否结束,若没有结束,则返回步骤②。

图2 基于KOHONEN 网络的聚类算法流程Fig.2 Flow chart of clustering algorithm based on KOHONEN network

基于KOHONEN 网络的电芯快速分选配组聚类算法流程如图2 所示。根据电芯分选数据的特点来初始化网络。 电芯分选数据有8 维,因此输入层节点数为8。 竞争层节点代表输入数据潜在的分类类别,考虑到沿用上述4 种分类的效果,选择竞争层节点数为4 个,将竞争层节点排列在2 行2 列的方阵中。

按式(5)计算和输入样本最接近的竞争层节点,作为该样本的优胜节点。

权值调整时,根据式(6)调整优胜节点领域半径r内的节点权值,其中领域半径和学习速率随着进化过程的深入逐渐变小。 这样,输入数据逐渐向几个节点集中,从而实现网络聚类的功能。

2.5 广义神经网络回归聚类算法

电池电芯的快速分选配组,需要考虑电压、电阻、电池温度和压差等多种因素,传统的聚类法,如系统聚类法、FCM 聚类法和K 均值聚类法都存在一定的缺陷和局限性。 在这些方法的基础上,本文作者提出使用一种改进聚类分析的神经网络集成方法[5]。

模糊聚类法虽然能够对电池电芯进行聚类分选,但是由于不同电池的各项参数差别较小,导致部分电池电芯不能准确分类。 采用结合模糊聚类和广义神经网络回归的聚类算法对电池进行分类,流程如图3 所示。

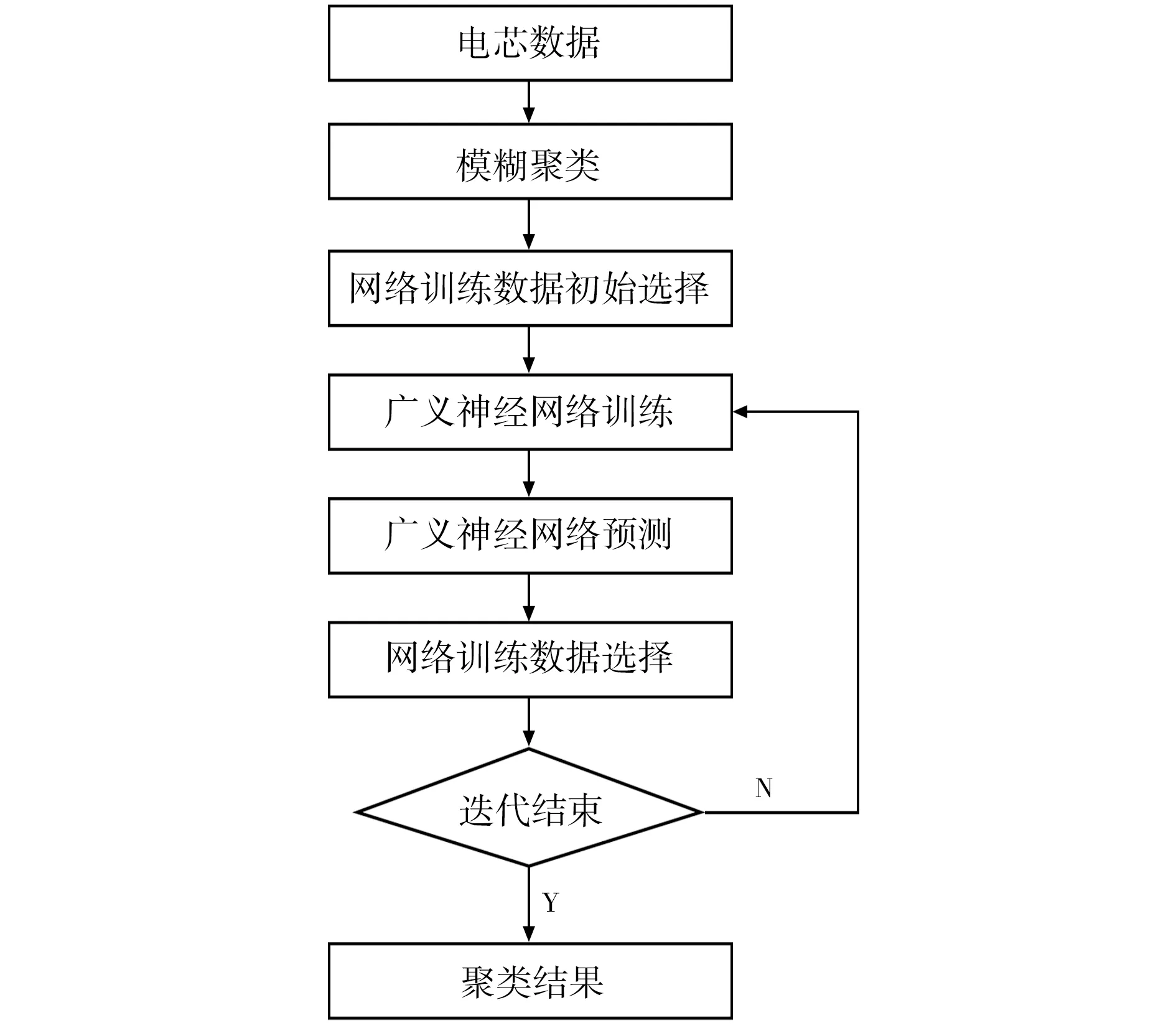
图3 基于广义回归神经网络的聚类算法流程Fig.3 Flow chart of clustering algorithm based on generalized regression neural network

广义神经网络聚类的具体方法如下:首先,用训练数据训练广义神经网络,使网络具有电芯快速分选配组的能力;然后,用训练好的广义神经网络来预测样本所属的类别,并根据预测结果对样本重新进行分类;最后,根据样本重新分类的结果,计算每类的中心,并重新选择离中心最近的数据,作为网络训练数据。 按照上述步骤反复迭代聚类,最终得到分类结果。

2.6 聚类分选结果横向比较

电压是电芯一致性判断的一项重要指标。 为了验证不同聚类分析算法下分选结果的有效性,将电压作为聚类分析分选结果的评价指标。 将充电截止电压(Uce)定义为x轴,放电1 h 电压(U1h)为y轴,放电截止电压(Ude)为z轴,对950 只电芯的数据以不同类别构建三维散点图,分选效果如图4 所示。

图4 4 种聚类算法效果图 Fig.4 Effect diagrams of four clustering algorithms

从图4 可知,4 种电芯聚类方法的分选结果整体良好。 系统聚类法、FCM 聚类法和广义神经网络回归聚类法的分选结果相似,分成类似“田”字的4 个模块,在部分数据分组交界的位置,分类稍有差异,分组结果区分度明显,符合电芯一致性分选配组的原则。 基于KOHONEN 网络聚类算法的分选结果与其他聚类算法略有不同,最上方左右各有一类,中间分为一类,下方分为一类,最上方两类表现为充电截止电压和放电1 h 的电压较为一致,而中间和下方这两类表现为放电截止电压较一致,整体上也达到了电芯一致性分选配组的效果。

除了利用三维散点图直观判断分选结果外,进一步通过计算分选前后充电截止电压和压差的标准差变化来验证分选结果的有效性。 先对符号进行相关定义。

σ(U0)为恒流-恒压充电的电压(即充电截止电压)的标准差;σ′(U0)为分选后所述类别充电截止电压的标准差;Δσ(U0)为对电芯进行分选前后的充电截止电压标准差的下降百分比,计算公式为:

σ(ΔU0)为恒流-恒压充电的压差的标准差;σ′(ΔU0)为分选后所述类别恒流-恒压充电的压差的标准差;Δσ(ΔU0)的计算公式为:

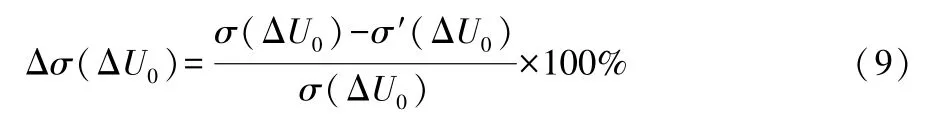
标准差能反映数据集的离散程度,能更好地判断电芯分选结果是否符合一致性原则,比较分选前后的充电截止电压与压差的标准差变化百分比,有助于深入分析分选效果。

4 种聚类算法的分选结果如表2 所示。

从表2 可知,电芯采用系统聚类法、FCM 聚类法、基于KOHONEN 网络聚类法和广义神经网络回归聚类算法进行分选,可降低充电截止电压和压差的标准差,以满足电池分选一致性的原则。 从充电截止电压的标准差来看,分选效果从好到差依次是:广义神经网络回归聚类法、FCM 聚类法、系统聚类法和基于KOHONEN 网络聚类法;从压差的标准差来看,分选效果从好到差依次是:KOHONEN 网络聚类法、广义神经网络回归聚类法、FCM 聚类法和系统聚类法。

由此可见,广义神经网络回归聚类法的整体分选效果最好,基于KOHONEN 网络聚类法在降低电芯电压差的标准差,从而提高一致性方面展现出良好的效果。 相较于传统的系统聚类法和FCM 聚类法,基于KOHONEN 网络聚类法和广义神经网络回归聚类法的锂离子电芯一致性的分选,配组效果更佳,可为实际工程应用提供参考。

表2 4 种聚类算法分选结果的比较 Table 2 Comparison of sorting results of four clustering algorithms

3 结论

本文作者基于1 024 只锂离子电池电芯的相关参数,结合电芯一致性原则,确定电芯分选的变量,采用系统聚类法、FCM 聚类法、基于KOHONEN 网络聚类法和广义神经网络回归聚类法对锂离子电池电芯进行快速分选配组,最后,多维度评价电芯一致性分选配组效果。

实验结果表明:相较于传统的系统聚类法和FCM 聚类法,基于KOHONEN 网络聚类法和广义神经网络回归聚类法的锂离子电芯一致性的分选配组效果更好。 摒弃传统的单体电芯分选法,提出使用神经网络对电芯进行快速分选配组,即基于KOHONEN 网络的聚类法和广义神经网络回归聚类法。 今后的研究可进一步考虑其他锂离子电池电芯分选算法,与现有的分选方法进行多维度的对比,以达到电芯一致性下更高的分选效率和更优的配组效果。