考虑σ2及围岩—支护结构相互作用的隧道力学模型
2021-07-10刘红岩
刘红岩
(1.中国地质大学(北京)工程技术学院,北京 100083;2.自然资源部深部地质钻探技术重点实验室,北京 100083)
0 引 言
目前新奥法已在隧道建设中得到了广泛应用,其认为围岩不仅是荷载来源,更是承载结构,支护的目的就是要充分调动围岩本身的承载能力[1-2]。由此隧道施工理论与实践均得到了快速发展,许多学者也都对围岩—支护结构的相互作用机理展开了深入研究[3-4]。基于岩石理想弹塑性模型及Mohr-Coulomb(M-C)强度准则,Kastner[5]较早地提出了围岩—支护相互作用的力学模型,这为隧道支护理论研究奠定了基础。然而,随着隧道工程的日益复杂,Kastner方法已不能很好地描述隧道的力学行为。为此,不少学者都对该问题进行了深入研究,从大的方面来说,主要集中在以下3方面:岩石本构模型、强度准则及围岩—支护结构的相互作用。
首先,目前已提出了很多能够考虑岩石摩擦、剪胀及时间效应的岩石本构模型来描述隧道围岩的力学行为。Gonzalez-Nicieza等[6]提出了考虑隧道埋深、形状和不同岩石本构模型的围岩力学响应曲线。Cheng[7]发现在塑性区范围内的围岩尤其是软岩体积膨胀较大,因此通过考虑塑性区内的围岩体积变化对Kastner公式进行了修正。Wang等[8]针对粘弹性岩石中的深埋双隧道,采用Brugers和Poyting-Thomson粘弹性本构模型得到了相应的解析解。Bian和Liu[9]引入了一个新的损伤变量来描述脆性岩石峰后的应变软化行为,并发现当考虑岩石脆性损伤后,相比岩石理想弹塑性模型而言,此时围岩塑性区范围将变大。Park和Kim[10]采用基于非关联流动法则的岩石弹—脆—塑性本构模型推导了圆形隧道围岩的位移解析解。总之,可以看出采用更为合适的岩石本构模型来研究隧道围岩的力学行为将是今后的发展趋势。
其次,对岩石强度准则的研究也逐渐成为目前的研究热点,这是因为不同的强度准则将导致隧道围岩塑性区范围大小的差异,进而影响到隧道的开挖与支护设计[11]。目前常用的岩石强度准则如MC、Drucker-Prager(D-P)和Hoek-Brown等均在隧道工程中有着一定应用[12-14]。但是由于M-C和Hoek-Brown准则均未考虑中间主应力σ2的影响,因此能够考虑σ2的D-P准则常常被用来替换M-C准则以研究中间主应力对隧道力学行为的影响,且研究结果表明中间主应力对围岩塑性区确实有一定影响,且随着中间主应力的增加,围岩承载能力也有所提高[15-16]。而尽管D-P准则能够很好地考虑了σ2的影响,但是却不能反映岩石不同子午线强度的差别,因此,Yu[17]提出了统一强度理论,并将其引入隧道力学分析以考虑σ2对隧道力学特性的影响。因此,选择合适的岩石强度准则对隧道围岩塑性区范围的准确确定至关重要。
最后,针对围岩—支护结构的相互作用问题,Cai等[18]提出了一个新的解析方法以考虑锚杆与围岩的相互作用对隧道围岩力学特性的影响。Jeffrey等[19]研究了支护结构施作时机对隧道力学行为的影响,认为如果支护结构施加太快,将会在临时支护结构中产生较大应力。针对实际隧道施工特点,侯公羽等[20-21]认为Kastner方法存在以下3方面的不足,首先其认为围岩支护力与原岩应力同时作用、同步施加,这与实际工程不符;因为实际地下工程均是先受力(原岩应力)、后开挖、再支护;其次,其视支护力为主动支护力,一次性加载,也不甚合理,事实上除预应力锚杆支护可近似为主动支护力外,其余围岩支护力均可视为随围岩向隧道内变形的增大而增大的被动反力,是分次或逐渐施加的;第三,在实际施工中,支护结构不可能在隧道开挖完成后立即施加,因此在支护结构施设前,围岩必然会产生一定的初始变形;为此,其提出了考虑围岩—支护结构相互作用全过程的解析解。Su等[22]提出了考虑支护结构施设前围岩初始弹性变形的隧道力学模型。
然而尽管目前在圆形隧道力学行为研究方面已取得了较为丰硕的研究成果,但仍存在着一定的不足,如未能全面考虑σ2、支护结构施加前围岩的初始弹性位移、围岩—支护结构相互作用等因素对围岩位移及塑性区的影响,因而导致理论计算结果与实际不甚符合。为此,本项目拟采用能够考虑σ2的统一强度理论,并结合隧道实际施工特点,从围岩—支护结构相互作用机理出发,采用轴对称问题的理想弹塑模型对隧道力学行为进行深入研究,以提出一种能够更好地反映围岩—支护结构相互作用的圆形隧道力学模型,进而为相关工程设计提供参考。
1 圆形隧道力学模型及统一强度理论
1.1 圆形隧道力学模型
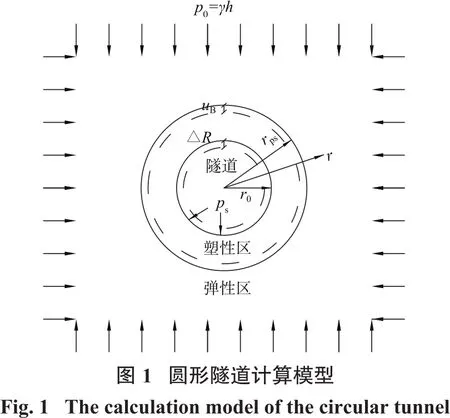
圆形隧道计算模型如图1所示,假设围岩为均质各向同性体,同时假设隧道四周受均布压力p0,其值取为隧道中心位置处的上覆土体自重γh,其中γ为围岩重度,h为隧道断面中心点的埋深。图中,uB和△R分别为隧道开挖后围岩弹性区和塑性区向隧道中心产生的位移;r0为隧道半径;rps为塑性区半径;r为围岩内任一点到隧道中心的距离;ps为支护力。隧道一般为线状结构物,即长度方向上的尺寸远大于其横断面尺寸,因此可视为平面应变问题。因此由于隧道结构和荷载的对称性,该问题为典型的轴对称问题,所以为求解方便,可采用极坐标进行求解。设σθ、σr、σz、εθ、εr、εz分别为圆形截面的环向、径向及轴向应力和应变,且应力之间满足σθ>σz>σr。由于隧道开挖,将导致围岩产生附加应力,当围岩附加应力超过岩石强度时将在围岩中产生塑性区,塑性区之外仍为弹性区。为此分别用“e”和“p”表示弹性区和塑性区的物理量。
1.2 统一强度理论
当隧道开挖以后,围岩应力调整,如果调整后的应力满足岩石塑性屈服条件,围岩将进入塑性区,而塑性区的范围则是隧道支护设计的关键参数,因此其合理确定至关重要。而为判断围岩是否进入塑性状态,则需要采用相应的强度准则,而不同的岩石强度准则也将导致不同的围岩塑性区。如前所述,M-C准则虽然能很好地反映岩土材料的压剪破坏本质,但却未能反映σ2的影响,因而无法解释岩石在高围压和静水压力下的屈服破坏现象。而D-P准则虽然很好地考虑了σ2的影响,但是却不能反映岩石不同子午线强度的差别[17]。为此,俞茂宏提出了适用于岩土类材料的统一强度理论[17]。
若设σ1、σ2和σ3分别为单元体的3个主应力,且σ1≥σ2≥σ3,这里取压应力为正。统一强度理论认为当单元体处于破坏状态时,主应力应满足[17]:
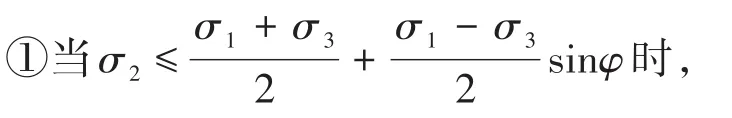

式中,c、φ分别为岩石黏聚力和内摩擦角;b为中间主应力系数,反映岩石破坏时σ2的影响,当b=0和1时,分别对应于M-C强度准则和双剪强度准则。
对于平面应变问题,当材料进入塑性状态时,纵向轴应力为σ2,假设岩石在变形过程中体积保持不变,即岩石泊松比μ=0.5,那么由平面应变的假设条件即垂直平面方向上的应变为零,即:

式中,E为岩石弹性模量。

对于采用极坐标时的圆形巷道,则有:

2 隧道开挖及支护后的围岩力学分析
假设隧道开挖后立即支护,那么由于开挖及支护的影响,岩体中的原始应力状态将发生调整。此时隧道周边的部分围岩将会进入塑性状态,由于结构及荷载均对称,因此在围岩中将形成一个半径为rps的塑性区,在塑性区外仍为弹性区,如图1所示。
2.1 围岩应力分析
首先对塑性区岩石受力进行分析,此时塑性区的应力分量应同时满足统一强度理论、平衡微分方程和应力边界条件,即:

由此可求得围岩塑性区内的应力分量为

假设弹塑性交界面上的径向应力为pf,由弹性力学可知,围岩弹性区的应力[23]为
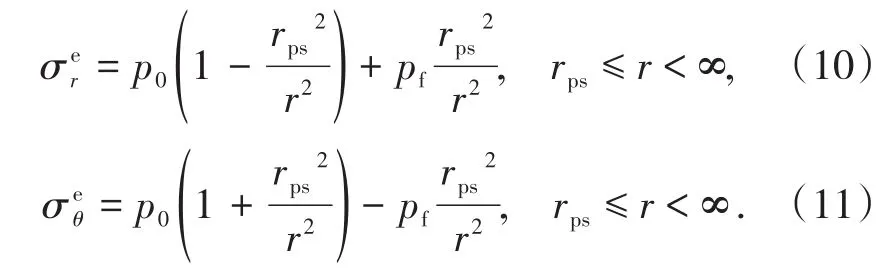
弹塑性交界面上的应力σr和σθ是连续的,因此,将r=rps代入式(8)~式(11)可得:

式(13)即为开挖及支护后的围岩塑性区半径。
2.2 围岩塑性区位移
如图1所示,分别设塑性区内、外边界处的位移分别为△R和uB。
首先求弹塑性交界面处的位移uB。设弹塑性交界面处的应力为σrep和σθep,那么二者应同时满足弹性条件和塑性条件。当满足弹性条件时,由式(10)、式(11)可得:

当满足塑性条件即式(5)所示的统一强度准则时,则有:

求解式(14)、式(15)可得弹塑性交界处的径向应力σrep为

塑性区位移的求解与塑性区体积变形假设有关,如前所述假设塑性区体积不变,则有:

由于隧道问题可视为平面应变问题,因此其几何方程为

代入式(17)可得:

积分并利用弹塑性区交界面上的变形协调条件,可得塑性区的径向位移(环向位移为0)为

将r=rps及式(16)代入式(20)可得塑性区外边界处的径向位移uB为

下面求解隧道洞壁位移ΔR。由于本文已假设岩体在变形过程中体积保持不变,即变形前塑性区岩石的体积与变形后的岩石体积相等。由此可得:

将式(21)代入式(22),并整理后可得:

将式(13)代入式(23),得到:

求解式(24)可得隧道洞壁位移:

2.3 考虑围岩—支护结构相互作用的围岩塑性区
然而由隧道实际施工过程可知,当隧道开挖完成以后,并不是等到隧道完全达到应力平衡及变形稳定以后才进行支护施工的,而是在隧道开挖完成但还没有达到一个新的应力平衡状态之前就已经开始支护了。然而此时还没有完全达到平衡状态的围岩必然还会继续进行应力调整,只是此时的应力调整将受到支护结构的约束,相应地支护结构的应力也会随着围岩的应力调整而发生变化。最终通过围岩—支护结构的相互作用而达到一个新的平衡状态。那么在此过程中,支护结构所提供的支护力ps肯定是一个动态变化的力。而在2.1节及2.2节中均视ps为定值,显然这是不合适的,造成这一问题的主要原因是没有考虑围岩—支护结构之间的相互作用。为此,下面拟从隧道工程实际施工过程及围岩—支护结构相互作用机理出发,研究支护力ps随围岩位移的变化规律,进而提出考虑围岩—支护结构相互作用的围岩塑性区计算方法。
围岩与支护结构相互作用特征曲线如图2。

由图2可以看出:
(1)在隧道开挖完成初期(如A点),围岩所需的支护约束力很大,而一般的支护结构所能提供的支护力则很小。因此围岩继续变形,相应地支护结构的约束阻力进一步增长,如果支护结构具有足够的强度和刚度,则围岩特征曲线和支护结构的支护补给曲线将会交于一点,而达到平衡。
(2)不同刚度的支护结构与围岩达成平衡时的ps和us是不同的,刚度大的支护结构承受的围岩压力也较大,如支护结构②和③,虽然我们在工程中强调采用柔性支护以节约成本,但其也应有必要的刚度,以有效控制围岩变形,从而达到稳定。如果支护结构刚度太小,如支护结构④,其支护补给曲线未能和围岩特征曲线相交,说明其提供的支护阻力不能满足围岩稳定的需要,最终将导致围岩失稳。
(3)同样刚度的支护结构,施加的时间不同,最终达到平衡的状态也将不同,如支护结构①和②。支护结构架设的越早,它所承受的围岩压力就越大,但这并不是说支护结构施做的时间越迟越好,因为如果围岩初始变形不能得到控制将会导致围岩迅速松弛而坍塌。因此原则上要尽早施做初期支护,以有效地控制围岩变形。
目前隧道支护常用的方法主要有混凝土支护、锚杆支护或其组合支护结构等,相对围岩力学特性而言,可以认为混凝土或钢支护结构的变形为线弹性。同时假设在隧道围岩变形过程中,支护结构与隧道围岩接触紧密,没有相对位移,那么支护结构总的径向位移就等于隧道内径处的径向位移。若假设支护结构提供的径向支护力ps与其在隧道内径处的径向位移△R成线性关系,则有:

式中,ks为支护结构刚度。由于这里仅考虑径向均布支护抗力,因此ks仅指支护结构受压(拉)刚度。
由于支护结构一般都是在隧道开挖后才施加的,而此时围岩已经出现了一定的初始径向位移(设为u0),则支护结构的支护力ps与其径向位移的关系可表示为

那么把式(27)分别代入式(13)和式(25)即可得到考虑支护结构刚度及施设时机的围岩塑性区半径rps及隧道洞壁位移ΔR分别为

u0为支护结构施设前隧道洞壁初始径向位移,基于对围岩保护的需要,因此一般要求支护结构在隧道围岩产生最大弹性变形之前施加,而施加支护前的隧道围岩最大弹性变形[24]为
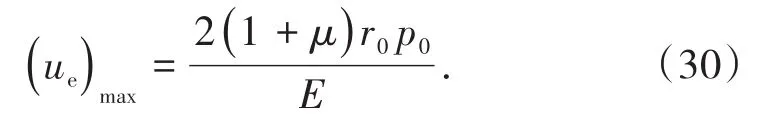
因此可取 0≦u0≦(ue)max。
由式(29)可知,该式两端均含有ΔR,很难求出其解析解,因此可采用迭代法求其数值解,然后把求出的△R代入式(28)计算围岩塑性区半径rps。
3 算例分析
某深埋圆形隧道的计算参数:r0=3 m,p0=15 MPa,E=10 GPa,c=1.0 MPa,φ=40°,ks=150 MPa/m。那么由式(30)可得(ue)max=0.011 25 m,因此这里取支护前隧道洞壁初始径向位移u0=0.005 m。下面对支护条件下隧道围岩力学特性进行研究。
3.1 围岩塑性区
采用rps/r0来表示塑性区的大小,那么由本文方法即式(28)可求得的围岩塑性区半径如图3所示。

由计算结果可知:围岩塑性区半径随着中间主应力系数b值的增加而降低,且当b=0和1时,rps/r0分别为1.372和1.239,即围岩塑性区减小了9.69%。同时为了进行对比分析,也给出了无支护时的计算结果,即式(28)中的ks(ΔR-u0)为0。可知当b=0和1时,rps/r0分别为1.551和1.335,即围岩塑性区减小了13.93%。由此可知:①中间主应力对围岩塑性区是有影响的,其影响幅度大约在10%~15%,且与隧道尺寸及围岩力学性质有关;②中间主应力对围岩塑性区的影响程度与围岩受力状态密切相关。当有支护时,隧道半径处的围岩径向应力不为零,该处围岩处于三向受力状态,此时中间主应力对围岩塑性区影响较小;而当无支护时,隧道半径处的围岩径向应力为零,该处围岩处于二向受力状态,此时中间主应力对围岩塑性区影响较大。这说明中间主应力对围岩塑性区的影响程度与围岩受力状态密切相关。
3.2 参数敏感性分析
下面采用参数敏感性分析(即每次仅改变其中一个参数,其他参数不变)讨论隧道洞壁初始径向弹性位移u0、支护结构刚度ks、初始地应力p0及岩石内摩擦角φ等对围岩相对塑性区rps/r0、隧道洞壁位移ΔR及支护力ps的影响。
(1)隧道洞壁初始径向弹性位移u0对计算结果的影响。取隧道洞壁初始径向弹性位移u0分别为0、0.002、0.004、0.006和0.008 m,计算结果如图4。可以看出:首先从u0对围岩塑性区的影响来看,当u0一定时,随着b的增加,围岩塑性区逐渐减小,这说明中间主应力可以有效减少围岩塑性区,进而提高其稳定性;随着u0的增加,隧道围岩塑性区呈逐渐增加的趋势,且其增加幅度逐渐变大;以b=1为例,当u0由0 m逐渐增加到0.002 m、0.004 m、0.006 m和0.008 m时,隧道围岩塑性区范围rps/r0则由1.164逐渐增加到1.191、1.222、1.256 和 1.296,其增加幅度分别为2.32%、2.60%、2.78%和3.18%;这说明虽然可以允许围岩产生一定的初始弹性变形,但是应限制在一定的范围内,否则过大的围岩初始弹性变形将会导致围岩塑性区的快速增加,进而导致围岩破坏。其次从u0对隧道洞壁位移的影响来看,当u0一定时,随着b的增加,隧道洞壁位移逐渐减小,这说明中间主应力可以有效减少隧道洞壁位移;随着u0的增加,隧道洞壁位移呈逐渐增加的趋势,且其增加幅度逐渐变大。因此为保证隧道有足够的净空,应尽可能地尽快支护,减小隧道洞壁初始弹性位移。最后从u0对支护力的影响来看,当u0一定时,随着b的增加,支护力也逐渐减小,这说明当考虑中间主应力的影响时,可以减少支护工程量,即中间主应力可以提高围岩稳定性;而随着u0的增加,支护力则是逐渐减小的,这说明如果允许围岩产生一定的初始弹性位移可有效减少支护工程量;但是相应地会使围岩塑性区增加、隧道断面净空减小,因此应综合考虑。

(2)支护结构刚度ks对计算结果的影响。取支护结构刚度ks分别为50、100、150、200和250 MPa/m,计算结果如图5所示。可以看出:首先从ks对围岩塑性区的影响来看,当ks一定时,随着b的增加,围岩塑性区逐渐减小,这说明中间主应力可以有效减少围岩塑性区,进而提高其稳定性;随着ks的增加,隧道围岩塑性区逐渐减小,且其减小幅度逐渐变小;以b=1为例,当ks由50 MPa/m逐渐增加到100、150、200和250 MPa/m时,隧道围岩塑性区范围rps/r0则由1.290逐渐减小到1.260、1.239、1.220和1.206,其减小幅度分别为2.36%、1.64%、1.52%和1.21%;这说明虽然提高支护结构刚度可以减小围岩塑性区,但是随着支护结构刚度的增加,隧道围岩塑性区的减小幅度是逐渐变小的,因此当支护结构刚度到一定程度后,其对围岩塑性区的影响就不甚显著。其次从ks对隧道洞壁位移的影响来看,当ks一定时,随着b的增加,隧道洞壁位移逐渐减小,这说明中间主应力可以有效减少隧道洞壁位移。而随着ks的增加,隧道洞壁位移则逐渐减小,且其减小幅度逐渐变小。最后从ks对支护力的影响来看,当ks一定时,随着b的增加,支护力也逐渐减小,这说明当考虑中间主应力的影响时,可以减少支护工程量,即中间主应力可以提高围岩稳定性;而随着ks的增加,支护力则是逐渐增大的,这说明提高支护结构刚度可以有效承担围岩荷载,减少围岩位移和塑性区;因此在安全性要求较高的隧道,可以考虑采用高刚度的支护结构进行支护。

(3)初始地应力p0对计算结果的影响。取初始地应力p0分别为10、12.5、15、17.5和 20 MPa,计算结果如图6所示。可以看出:首先从p0对围岩塑性区的影响来看,当p0一定时,随着b的增加,围岩塑性区逐渐减小,这说明中间主应力可以有效减少围岩塑性区,进而提高其稳定性;随着p0的增加,隧道围岩塑性区逐渐增大,且其增大幅度逐渐变小;以b=1为例,当p0由10 MPa逐渐增加到12.5、15、17.5和20 MPa/m时,隧道围岩塑性区范围rps/r0则由1.211逐渐增大到1.227、1.240、1.246 和 1.254,其增大幅度分别为1.32%、0.96%、0.57%和0.55%;这说明虽然初始地应力的增加将导致围岩塑性区的增大,但是当其增加到一定程度后,其对围岩塑性区的影响就不甚显著。其次从p0对隧道洞壁位移的影响来看,当p0一定时,随着b的增加,隧道洞壁位移逐渐减小,这说明中间主应力可以有效减少隧道洞壁位移;而随着p0的增加,隧道洞壁位移则逐渐增加,这说明地应力越大,相应地围岩位移就越大。最后从p0对支护力的影响来看,当p0一定时,随着b的增加,支护力也逐渐减小,这说明当考虑中间主应力的影响时,可以减少支护工程量,即中间主应力可以提高围岩稳定性;而随着p0的增加,支护力则是逐渐增大的,这说明当初始地应力较大时,相应地也需要更大的支护力才能保证围岩稳定。

(4)岩石内摩擦角φ对计算结果的影响。由于岩石内摩擦角和黏聚力都属于抗剪强度参数,因此这里仅以岩石内摩擦为例进行说明。取岩石内摩擦角φ分别为30°、32.5°、35°、37.5°和40°。由图7所示的计算结果可以看出:首先从φ对围岩塑性区的影响来看,当φ一定时,随着b的增加,围岩塑性区逐渐减小,这说明中间主应力可以有效减少围岩塑性区,进而提高其稳定性;随着φ的增加,隧道围岩塑性区逐渐减小,且其减小幅度逐渐变小;以b=1为例,当φ由30°逐渐增加到32.5°、35°、37.5°和40°时,隧道围岩塑性区范围rps/r0则由1.475逐渐减小到1.404、1.340、1.285和1.239,其减小幅度分别为4.85%、4.54%、4.11%和3.56%;这说明虽然提高岩石内摩擦角可以减小围岩塑性区,但是当岩石内摩擦角增加到一定程度后,其对围岩塑性区的影响就不甚显著。其次从φ对隧道洞壁位移的影响来看,当φ一定时,随着b的增加,隧道洞壁位移逐渐减小,这说明中间主应力可以有效减少隧道洞壁位移;而随着φ的增加,隧道洞壁位移则逐渐减小,且其减小幅度逐渐变小。最后从φ对支护力的影响来看,当φ一定时,随着b的增加,支护力也逐渐减小,这说明当考虑中间主应力的影响时,可以减少支护工程量,即中间主应力可以提高围岩稳定性;而随着φ的增加,支护力则是逐渐减小的,这说明随着岩石内摩擦角的增加,岩石强度提高,因而所需的支护力相应地会有所减小;因此可以通过注浆等方式提高岩石强度进而减少支护工程量。

4 模型验证
以朱艳峰等[25]给出的实际工程——兴隆隧道为例对本文提出的模型进行验证,该隧道位于重庆市渝北区木耳镇良桥村至金岗村之间,为双向四车道高速公路隧道,左线隧道全长2 553 m,主洞为三心圆曲墙结构,净高7.05 m,净宽10.66 m,内净空面积64.28 m2。在理论分析中,常常把曲墙拱形等接近圆形断面的洞室形状假设为圆形,即等代圆法。朱艳峰等[25]采用4种方法计算了等代圆半径,并采用现场声波探测法对围岩松动圈半径进行了测量,进而根据松动圈与塑性区的换算关系得到围岩塑性区半径,如表1。可以看出,尽管采用不同的方法计算出的隧道等代圆半径和塑性区半径有所不同,但是塑性区相对半径rps/r0却是相同的,因此可以用它来表征围岩塑性区大小。

工程区出露岩性为侏罗系中流上沙溪组砂岩。本次计算断面所处位置为Ⅳ级围岩,主要为中风化砂岩,岩体较完整,岩体弹性模量为5 882.8 MPa,泊松比0.17,原岩应力22.03 MPa,开挖后采用系统锚杆支护并挂设钢筋网,经计算支护力ps=4.8 MPa。由于本模型涉及到的其他参数文中均未给出,因此这里根据经验及岩土工程勘察规范给出:由于本工程中的围岩为Ⅳ级,因此取c=0.4 MPa,φ=30°,u0=0.01 m(<umax=0.042 m),ks=450 MPa/m。
下面采用本文提出的方法对围岩相对塑性区rps/r0和支护力ps进行了计算,结果如图8。

由图8可以看出:
(1)二者的理论计算结果随着b值的增加均逐渐减小,这主要是由于随着b值的增加,中间主应力对计算结果的影响也逐渐增加,这说明考虑中间主应力后,围岩塑性区及支护力均减小,即中间主应力对围岩稳定及改善支护结构受力是有利的。
(2)从理论计算结果与实测结果的对比来看,对围岩相对塑性区rps/r0而言,当b=0.7~0.8时,计算结果与实测结果最为接近;而对支护力ps而言,当b=0.5时,计算结果与实测结果最为接近。对于同一模型,中间主应力系数b则为一定值,但是由于在实际工程中,很难判断中间主应力究竟在多大程度发挥了作用,因此由于b=0~1且根据工程经验,这里取b=0.5为例进行研究,此时计算围岩相对塑性区rps/r0和支护力ps分别为1.299和4.815 MPa,而相应的实测结果则分别为1.277和4.8 MPa,因此二者的相对误差仅分别为1.72%和0.31%,因此可以认为二者的误差很小。
(3)如前所述,在实际工程中由于b值很难准确确定,但根据工程经验和理论分析认为其取值范围一般在0.3~0.8之间,图8给出了这个取值范围内的理论计算结果与实测结果的对比,可以看出在此范围内二者的误差较小。因此可以认为本文提出的理论模型是合理的。
5 结 论
(1)通过引入统一强度理论,获得了考虑σ2的隧道围岩塑性区及隧道洞壁位移计算公式。在此基础上,同时考虑隧道实际施工过程及围岩—支护结构相互作用机理,提出了同时考虑σ2、隧道围岩初始弹性位移及围岩与支护结构相互作用的隧道塑性区、隧道洞壁位移及支护力的计算方法,建立了相应的隧道力学模型。
(2)算例分析表明,当采用考虑σ2的统一强度理论时,相对于M-C准则而言,有支护和无支护两种情况下的围岩相对塑性区最大减小程度分别为10.09%和13.93%。同时通过参数敏感性分析发现随着隧道围岩初始弹性位移u0的增加,支护应力减小,但围岩塑性区和隧道洞壁位移增加;随着支护结构刚度ks的增加,围岩塑性区及隧道洞壁位移减小,但支护结构应力增加;初始地应力p0的增加将导致围岩塑性区、隧道洞壁位移及支护结构应力同时增加;随着岩石内摩擦角φ的增加,围岩塑性区、隧道洞壁位移及支护结构应力则均减小。
(3)将该模型应用于某一具体工程的力学分析,通过将由理论计算得到的围岩相对塑性区、支护力与相应实测结果的对比分析表明二者误差较小,验证了该模型的合理性。
(4)本文提出的考虑σ2及围岩—支护结构相互作用的力学模型,能够更好地反映隧道围岩的力学行为,这为圆形隧道力学特性研究提供了一条新思路。
