地方院校数学师范生TPACK的年级差异性分析——以青海省为例

王 煜，孔令钰，郭承育

地方院校数学师范生TPACK的年级差异性分析——以青海省为例

王 煜，孔令钰，郭承育

（青海师范大学 数学与统计学院，青海 西宁 810008）

TPACK是当今时代有效教学的基础，也是教师专业发展的关键性内容，地方院校数学师范生TPACK掌握情况直接影响该地区未来数学教学的质量．TPACK的掌握情况受到与教育者自身心理或外部条件等诸多因素的影响．研究将影响TPACK掌握情况的因素考虑在内，设计了“数学师范生TPACK调查问卷”，对青海省在校数学师范生进行了全样本调查．结果显示：青海省高校数学师范生所具备的CK、PK、PCK、TCK、TPK、TPCK均存在显著年级差异；各影响因素对不同年级数学师范生TPACK的影响强度均有不同．

地方院校；数学师范生；TPACK；年级差异

1 问题提出

针对早期教师教育研究只关注教师的学科知识（CK）或者只关注教师的教学知识（PK）这一现象[1-2]，舒尔曼[3-4]提倡需要探索这两种知识之间的内在关系，提出了学科教学知识（PCK）．这一概念的提出标志着基于学科背景的教师知识研究的开始，教师如何把他们拥有的学科知识转化为一种学生能够理解的知识直接影响着学生的有效学习，因此PCK被视为教学知识基础的核心部分[5]，也使得人们深刻地意识到了教师专业化的特点．随着时代的发展，教师发现在教学实践中，仅仅掌握足够的数学学科知识，具备丰富的教学法知识与教学经验是远远不够的，还必须掌握能够提高教学效果的相应的信息技术知识（TK）．因此，为了使教师理解信息技术与学科知识及教学法知识之间的关系，科勒和米什拉拓展了PCK框架，提出了包容性更强的框架——整合技术的学科教学知识（TPACK）[6-8]．随着教育学者对TPACK研究的逐渐深入[9-10]，人们意识到教师学习、掌握和应用TPACK往往需要与自身心理或外部条件等诸多因素协同作用[11]．目前在TPACK的研究中缺乏对其影响因素的深入分析，这已经成为TPACK研究进一步发展的主要障碍．

中国地大物博、幅员辽阔、教育发展不均衡，如今正处在教育信息化发展十年改革的收尾阶段[12]．青海地处祖国西部，是多民族地区，教育发展相对滞后，该地区数学师范生的TPACK掌握程度直接影响着该地区未来数学教学的质量，对青海省高校数学师范生TPACK的研究可以为中国教育信息化整体发展情况提供参考依据．

基于对国内外TPACK基础问题以及影响TPACK的因素进行文献梳理，至今还未见有专门研究TPACK在不同年级之间差异性的文献．因此，研究从影响因素角度对青海省高校数学师范生TPACK的年级差异性进行研究，以期了解青海省高校数学师范生TPACK的年级差异性以及各影响因素对不同年级数学师范生TPACK的影响方式及影响强度，从而针对各影响因素对不同年级数学师范生TPACK的影响方式及影响强度的不同，对数学师范生TPACK的发展提出建议．

2 研究设计

2.1 研究思路

在明确已有研究成果的基础上，参照国内外已使用的TPACK测试量表以及前人对TPACK的影响因素的研究总结[13]，修改、编制“数学师范生TPACK调查问卷”，通过问卷调查收集数据，使用SPSS20.0[14]和AMOS24.0[15-16]软件对调查数据进行统计分析，由此对该地区高校数学师范生TPACK的培养提出建议．

已有研究对TPACK的使用分别指代如下两个含义：（1）为强调整体性，指代TPACK框架，其中包含7个元素；（2）指代7个元素中的一个，由TK、PK、CK3个核心知识交叉而形成的复合元素TPACK．为区分上述两种含义，研究认为TPCK指代复合元素，以TPACK指代整体框架[17]．

2.2 研究工具

“数学师范生TPACK调查问卷（预测）”的信度、效度分析以该地区某高校的数学与统计学院数学（师范）专业大一～大四年级的学生为预测样本，在2019年4月底统一发放问卷164份，回收问卷时对关键信息缺失和每个题项选择相同的无效问卷进行了剔除，共回收有效问卷151份，运用SPSS 20.0对收集的数据进行信效度检验．初次检验测得该问卷取样适当性量数KMO值为0.900，继续开展因子分析测得47个题项变量的变量共同度中有6个题项在提取因子后已经损失了原始变量的大部分信息，因此问卷应剔除该6个题项．剔除6个题项后再次检验该问卷的KMO值仍为0.900，说明剔除6个题项后量表仍适合进行因子分析，41个题项的变量共同度都在0.7以上，说明该问卷的41个题项均应保留．经由后续分析可知，所有题项均在预设的维度之中，所以该问卷具有良好的结构效度．最终由41个题项组成的“数学师范生TPACK调查问卷”的信度统计量系数值为0.957，表示该问卷整体具有良好的信度．

研究使用的“数学师范生TPACK调查问卷”由3部分组成，第一部分是基本信息，共一道题目，用于调查被测试者的年级；第二部分是TPACK现状调查，共25道单项选择题，用于调查青海省高校数学师范生TPACK现状，其中T1～T4题测试TK维度、T5～T7题测试CK维度、T8～T12题测试PK维度、T13～T15题测试PCK维度、T16～T18测试TCK维度、T19～T22测试TPK维度、T23～T25测试TPACK维度；第三部分是TPACK的影响因素调查，共16道单项选择题，用于调查青海省高校数学师范生TPACK的影响因素，其中I1～I3题测试教师职业认同因素、I4～I6题测试动机和自我效能感因素、I7～I9题测试教育技术课程因素、I10～I11题测试教学实践经历因素、I12～I16题测试学校资源与环境因素．问卷的第二部分和第三部分题目选项均为“完全符合”“基本符合”“中立”“不太符合”和“完全不符合”，采用李克特5点式计分．

2.3 研究对象

选取青海省3所高校数学（师范）专业的学生进行全样本调查，共计对560名学生发放问卷，排除无效问卷，回收有效问卷476份，研究对象具体分布情况见表1．

表1 研究对象分布

3 研究过程

3.1 TPACK七维度的年级差异性分析

研究使用单因素方差分析法对数学师范生的TPACK七维度分别进行年级差异性分析．首先对数学师范生的TPACK七维度分别进行方差齐性检验，分析可知不同年级数学师范生的TK、PK、TPK、TPCK维度的方差齐性检验的值小于0.05，表明方差不满足齐性，需要用Tamhane方法进行后续方差分析，而CK、PCK、TCK维度的方差齐性检验的值大于0.05，表明方差满足齐性，需要用LSD方法进行后续方差分析．不同年级数学师范生在TPACK七维度的差异性分析见表2．

由表2可知，数学师范生仅TCK维度大四年级高于其它年级，其它六维度均为大三年级高于其它年级；差异的显著性值仅TK维度为0.148>0.05，表明4个年级数学师范生所具备的TK不存在显著差异，其余六维度差异的显著性值均为0.000<0.05，表明4个年级数学师范生所具备的CK、PK、PCK、TCK、TPK、TPCK均存在显著差异．

3.2 TPACK六维度的多重比较分析

不同年级数学师范生在CK、PK、PCK、TCK、TPK、TPCK维度上的多重比较结果见表3所示．

由表3可知，对不同年级数学师范生具有显著差异的六维度做年级间的多重比较后发现，数学师范生在CK维度上各个年级之间均存在显著差异；在PK、PCK维度上大一、大二与其它各年级均存在显著差异，大三与大四年级不存在显著差异；在TCK维度上大一与其它各年级均存在显著差异，大二与大三、大四年级均不存在显著差异，大三与大四年级不存在显著差异；在TPK维度上大一与其它各年级均存在显著差异，大二与大三年级存在显著差异、与大四年级不存在显著差异，大三与大四年级不存在显著差异；在TPCK维度上大一与其它各年级均存在显著差异，大二与大三年级存在显著差异、与大四年级不存在显著差异，大三与大四年级存在显著差异．

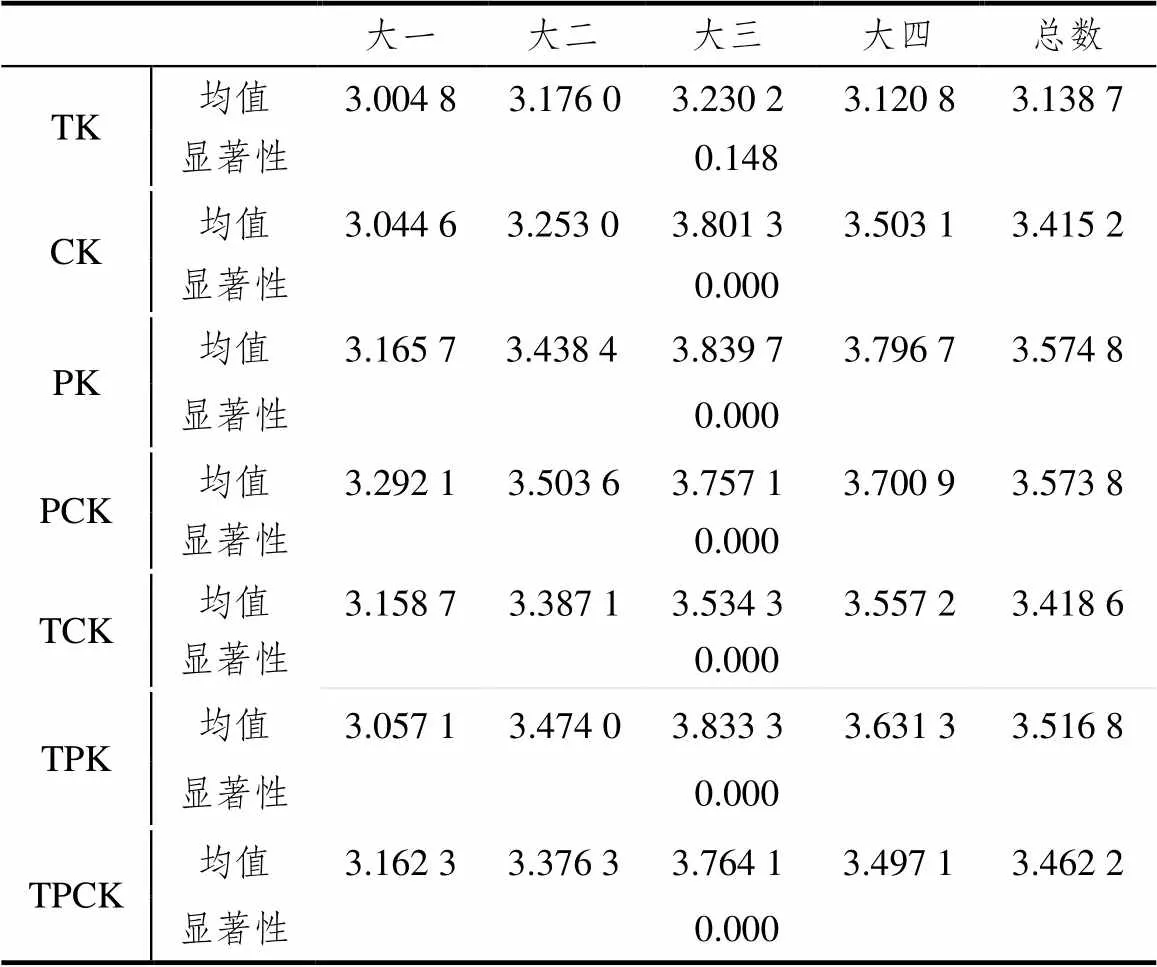
表2 数学师范生TPACK七维度的年级差异性分析

3.3 不同年级数学师范生TPACK影响因素的路径分析

由上述分析可知，总体来讲大三年级数学师范生的TPACK高于其它年级且4个年级数学师范生所具备的TPACK存在显著差异．为了探究TPACK存在着显著年级差异的原因是否是由于问卷中的这5个影响因素对其的影响方式不同而造成的，接下来便使用结构方程模型法对影响因素与不同年级数学师范生TPACK的关系进行研究．因研究是小样本研究，故选用拟合优度指数（）、平均概似平方误根系数（）、比较适合度指数（）和塔克尔勒威斯指数（）4个指标评价模型的拟合度．每个模型均首先进行拟合度与路径系数显著性检验，然后再借助该模型进行模型估计值的计算．为节约篇幅，仅对第一个模型完整地呈现出拟合指数表、路径系数表、标准化路径系数表，并展示完整模型图，其后的模型均只呈现出模型的拟合指数与最终简化过的路径系数图，对于数据分析过程中的图表不再进行大篇幅赘述．

3.3.1 大一年级数学师范生TPACK影响因素的路径分析

经过AMOS24.0对模型进行前期的拟合与修正，得到大一年级数学师范生TPACK影响因素模型的拟合指数见表4，模型的路径系数见表5．

由表4、表5可知，大一年级数学师范生TPACK影响因素模型与数据拟合度较好，且模型中的每条路径系数值都小于0.05，表明借助该模型可以进行模型估计值的计算．最终确定的大一年级数学师范生TPACK影响因素模型如图1所示，模型的标准化路径系数见表6所示，模型的路径系数图如图2所示．

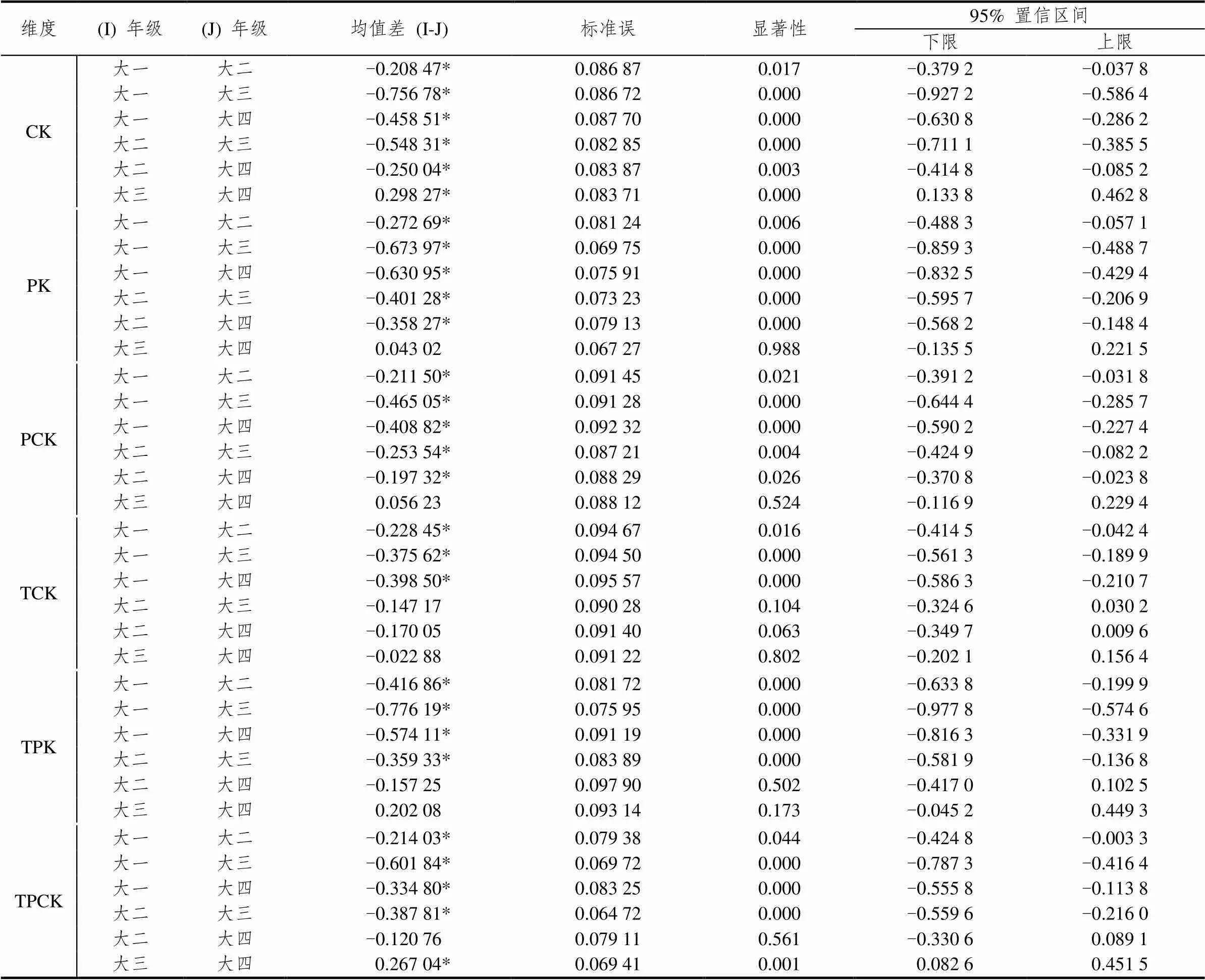
表3 不同年级数学师范生在六维度上的多重比较

注：*表示均值差的显著性水平为0.05

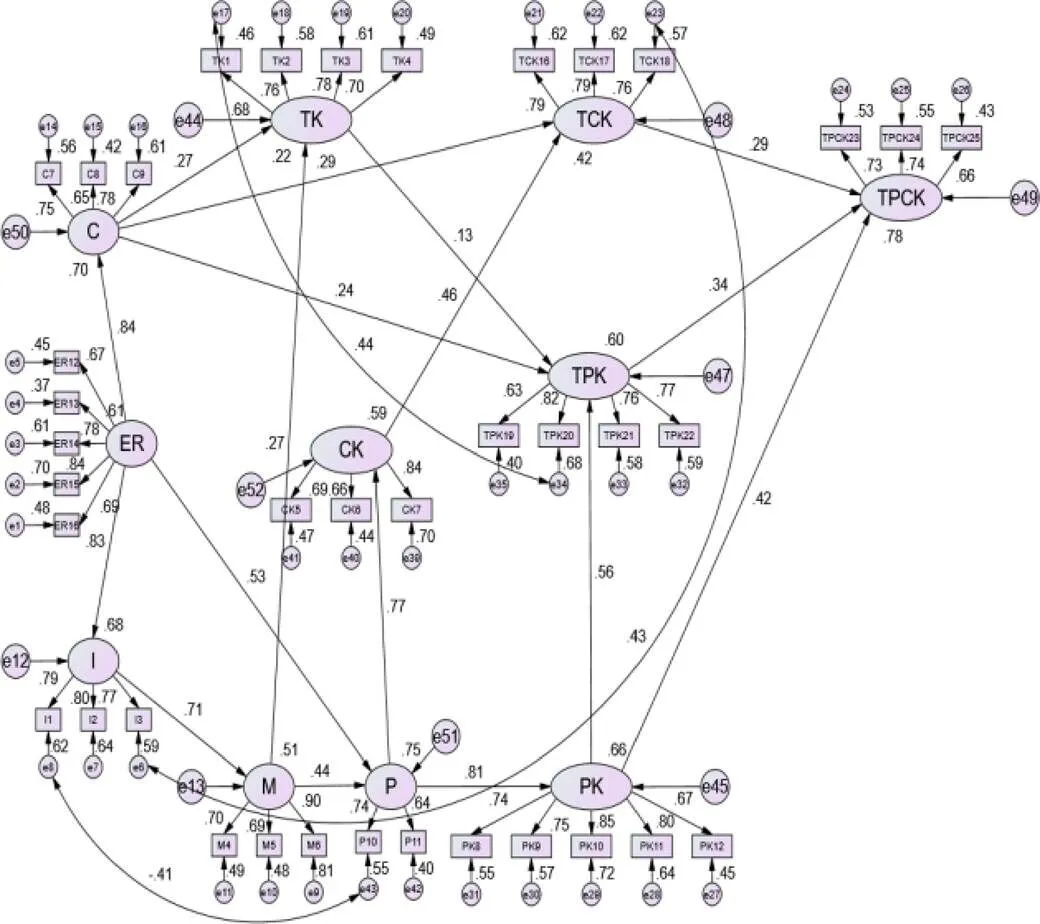
图1 大一学生TPACK影响因素模型

表4 大一学生TPACK影响因素模型的拟合指数

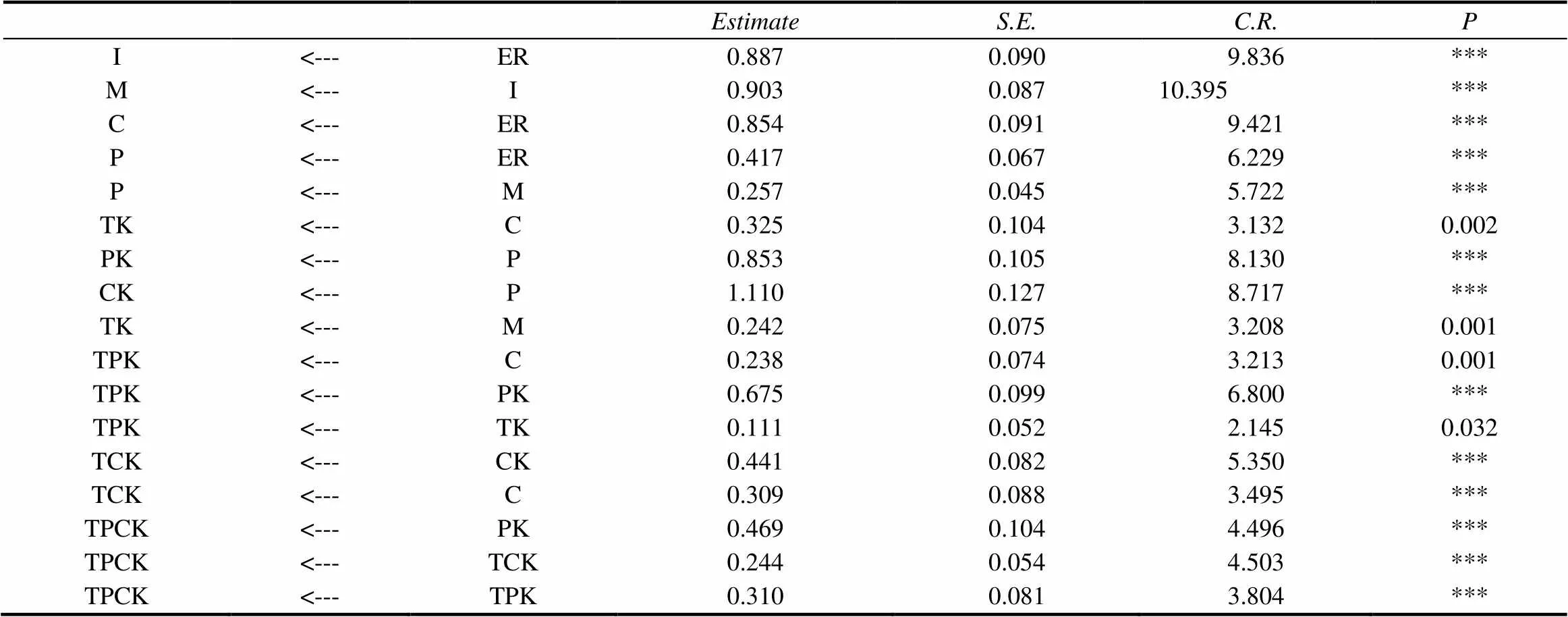
表5 大一学生TPACK影响因素模型的路径系数

由表6和图2可知，大一年级数学师范生TPACK影响因素的模型中共有17条路径，该模型展示了所假设的5个影响因素是如何影响大一年级数学师范生TPACK的．通过路径分析，得出以下结果．

（1）假设5个影响因素对大一年级数学师范生的TPACK有影响，该假设成立．

（2）教师职业认同（I）对大一年级数学师范生TPCK的影响只有间接效应，影响的总强度为0.198，有4条轨迹：① I→M→TK→TPK→TPCK=0.714×0.272×0.132×0.342=0.009；② I→M→P→CK→TCK→TPCK=0.714×0.442×0.767×0.458 ×0.293=0.032；③ I→M→P→PK→TPK→TPCK=0.714×0.442 ×0.81×0.555×0.342=0.049；④ I→M→P→PK→TPCK=0.714 ×0.442×0.81×0.425=0.109．

（3）动机和自我效能感（M）对大一年级数学师范生TPCK的影响只有间接效应，影响的总强度为0.278，有4条轨迹：① M→TK→TPK→TPCK=0.272×0.132×0.342=0.012；② M→P→CK→TCK→TPCK=0.442×0.767×0.458×0.293= 0.045；③ M→P→PK→TPK→TPCK=0.442×0.81×0.555×0.342=0.068；④ M→P→PK→TPCK=0.442×0.81×0.425=0.152．

（4）教育技术课程（C）对大一年级数学师范生TPCK的影响只有间接效应，影响的总强度为0.178，有3条轨迹：① C→TK→TPK→TPCK=0.274×0.132×0.342=0.012；② C→TCK→TPCK=0.286×0.293=0.084；③ C→TPK→TPCK=0.24×0.342=0.082．

（5）教学实践经历（P）对大一年级数学师范生TPCK的影响只有间接效应，影响的总强度为0.601，有3条轨迹：① P→CK→TCK→TPCK=0.767×0.458×0.293=0.103；② P→PK→TPK→TPCK=0.81×0.55×50.342=0.154；③ P→PK→TPCK=0.81×0.425=0.344．

（6）学校资源与环境（ER）对大一年级数学师范生TPCK的影响只有间接效应，影响的总强度为0.630，有10条轨迹：① ER→I→M→TK→TPK→TPCK=0.826×0.714×0.272×0.132×0.342=0.007；② ER→I→M→P→CK→TCK→TPCK=0.826×0.714×0.442×0.767×0.458×0.293=0.027；③ ER→I→M→P→PK→TPK→TPCK=0.826×0.714×0.442×0.81×0.555×0.342=0.040；④ ER→I→M→P→PK→TPCK=0.826×0.714×0.442×0.81×0.425=0.090；⑤ ER→C→TK→TPK→TPCK=0.837×0.274×0.132×0.342=0.010；⑥ ER→C→TCK→TPCK=0.837×0.24×0.293=0.070；⑦ ER→C→TPK→TPCK=0.837×0.24×0.342=0.069；⑧ ER→P→CK→TCK→TPCK=0.527×0.767×0.458×0.293=0.054；⑨ ER→P→PK→TPK→TPCK=0.527×0.81×0.555×0.342=0.081；⑩ ER→P→PK→TPCK=0.527×0.81×0.425=0.181．

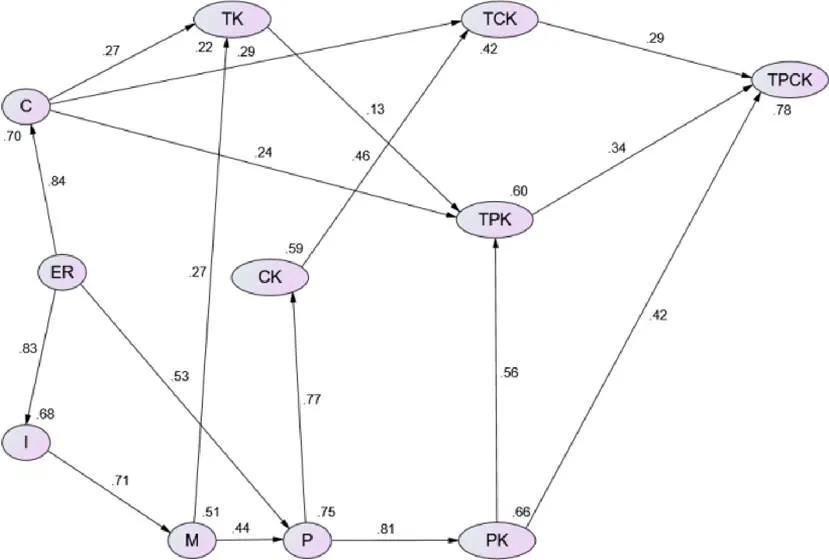
图2 大一学生TPACK影响因素模型路径系数

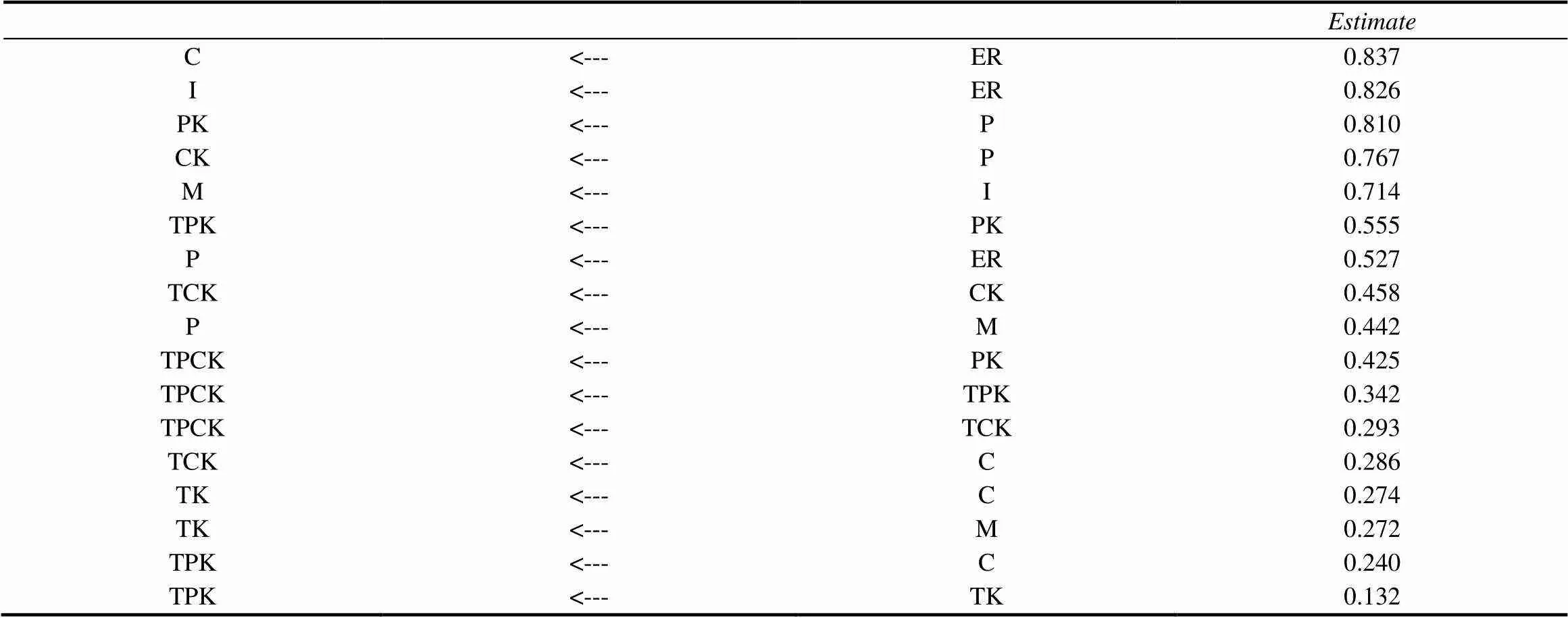
表6 标准化路径系数

3.3.2 大二年级数学师范生TPACK影响因素的路径分析

最终确定的大二年级数学师范生TPACK影响因素模型的拟合指数见表7所示，模型的路径系数图如图3所示．

表7 大二学生TPACK影响因素模型的拟合指数

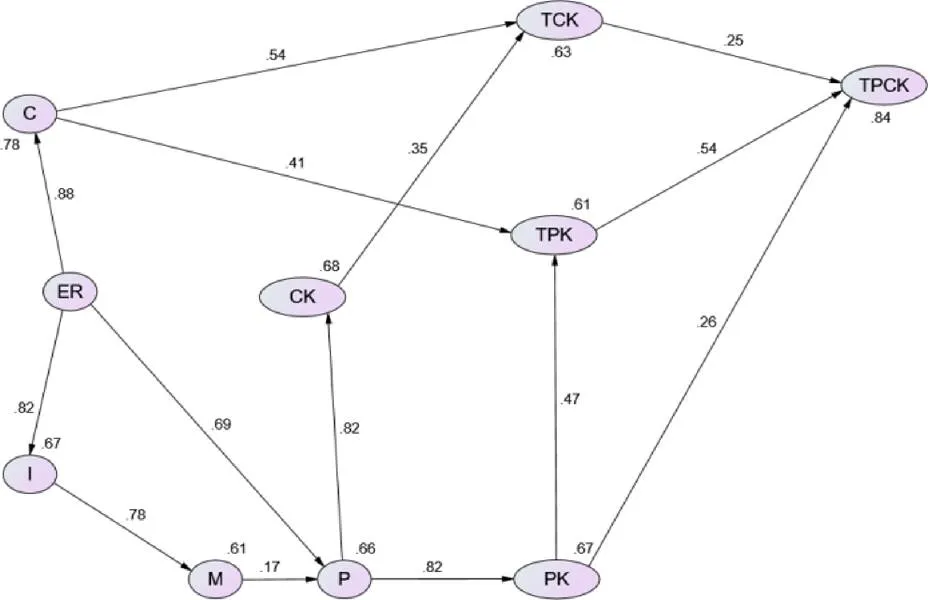
图3 大二学生TPACK影响因素模型路径系数

由表7可知，大二年级数学师范生TPACK影响因素模型与数据拟合度较好，可以进行模型估计值的计算．由图3可知，大二年级数学师范生TPACK影响因素的模型中共有14条路径，模型的路径分析按照大一年级数学师范生TPACK模型的分析方式进行，详细过程便不再赘述，得出以下结果．

（1）假设5个影响因素对大二年级数学师范生的TPACK有影响，该假设成立．

（2）教师职业认同影响大二年级数学师范生TPCK的总强度为0.066．

（3）动机和自我效能感影响大二年级数学师范生TPCK的总强度为0.085．

（4）教育技术课程影响大二年级数学师范生TPCK的总强度为0.354．

（5）教学实践经历影响大二年级数学师范生TPCK的总强度为0.492．

（6）学校资源与环境影响大二年级数学师范生TPCK的总强度为0.707．

3.3.3 大三年级数学师范生TPACK影响因素的路径分析

最终确定的大三年级数学师范生TPACK影响因素模型的拟合指数见表8所示，模型的路径系数图如图4所示．

表8 大三学生TPACK影响因素模型的拟合指数

图4 大三学生TPACK影响因素模型路径系数

由表8，大三年级数学师范生TPACK影响因素模型与数据拟合度较好，借助该模型可以进行模型估计值的计算．由图4可知，大三年级数学师范生TPACK影响因素的模型中共有15条路径，模型的路径分析按照大一年级数学师范生TPACK模型的分析方式进行，详细过程便不再赘述，得出以下结果．

（1）假设5个影响因素对大三年级数学师范生的TPACK有影响，该假设成立．

（2）教师职业认同影响大三年级数学师范生TPCK的总强度为0.133．

（3）动机和自我效能感影响大三年级数学师范生TPCK的总强度为0.265．

（4）教育技术课程影响大三年级数学师范生TPCK的总强度为0.285．

（5）教学实践经历影响大三年级数学师范生TPCK的总强度为0.149．

（6）学校资源与环境影响大三年级数学师范生TPCK的总强度为0.667．

3.3.4 大四年级数学师范生TPACK影响因素的路径分析

最终确定的大四年级数学师范生TPACK影响因素模型的拟合指数见表9所示，模型的路径系数图如图5所示．

由表9，大四年级数学师范生TPACK影响因素模型与数据拟合度较好，借助该模型可以进行模型估计值的计算．由图5可知，大四年级数学师范生TPACK影响因素的模型中共有11条路径，模型的路径分析按照大一年级数学师范生TPACK模型的分析方式进行，详细过程便不再赘述，得出以下结果．

（1）假设5个影响因素对大四年级数学师范生的TPACK有影响，该假设成立．

（2）教师职业认同影响大四年级数学师范生TPCK的总强度为0.048．

（3）动机和自我效能感影响大四年级数学师范生TPCK的总强度为0.062．

（4）教育技术课程影响大四年级数学师范生TPCK的总强度为0.163．

（5）教学实践经历影响大四年级数学师范生TPCK的总强度为0.200．

（6）学校资源与环境影响大四年级数学师范生TPCK的总强度为0.408．

表9 大四学生TPACK影响因素模型的拟合指数

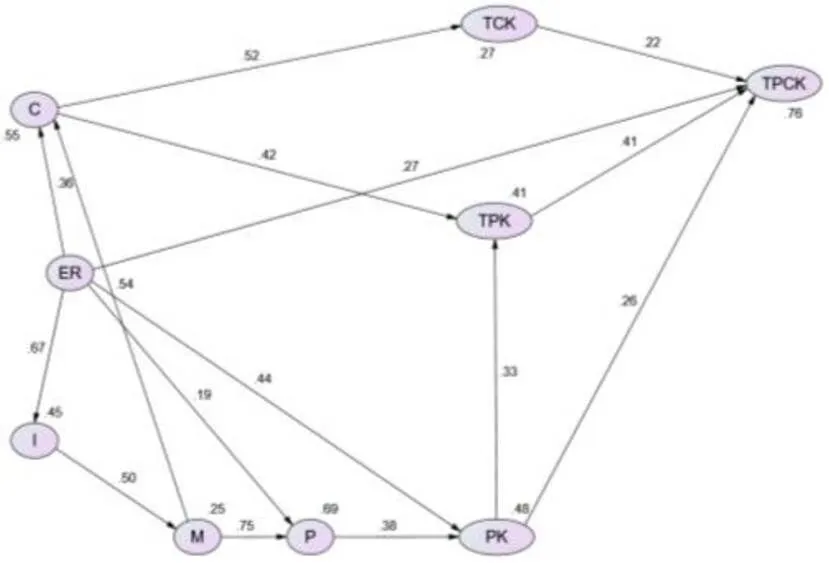
图5 大四学生TPACK影响因素模型路径系数

4 结论与启示

（1）数学师范生仅TCK维度大四年级高于其它年级，其它六维度均为大三年级高于其它年级；数学师范生所具备的CK、PK、PCK、TCK、TPK、TPCK均存在显著年级差异．结合后续多重比较分析可知，数学师范生在经过大二、大三学年的学习后其CK、PK、PCK、TPK、TPCK均有显著提升，其TCK则仅是经过大二学年的学习后有显著提升；数学师范生在经过大四学年的教育实习后，仅TCK有所提升，其余CK、PK、PCK、TCK、TPK、TPCK均有下降，其中CK和TPCK下降较为显著．由此表明，青海省目前的各中小学教育单位还缺乏可以对新手教师进行继续教育的资源与途径，数学教师队伍的TPACK还有待提升．

（2）数学师范生所具备的TPACK存在年级差异的一个原因可能为5个影响因素对不同年级数学师范生TPACK的影响路径不尽相同．从各个模型的路径系数图可知，5个影响因素对大一年级数学师范生的TK、CK、PK这3个基础知识影响较大；对大二、大三年级数学师范生的TCK、TPK这两个复合知识影响较大；而大四年级数学师范生受该5个影响因素影响的知识只有PK和TPK，且系数均不大．由此表明，青海省高校对大一年级数学师范生的课程设置较为合理，注重学生基础知识的学习，而对大二、大三年级数学师范生的课程设置上仅注重了将教育技术直接与学科知识、教学法知识进行融合，而没有对基础知识再加以巩固，这也就导致了大四年级数学师范生是在基础知识不牢固的前提下进入教育实习环节，加上实习学校的在职教师TPACK薄弱，无法辅导实习生处理教育实习阶段突发的教育技术问题，从而使实习生不敢用、不想用技术知识辅助教学，渐渐丧失使用教育技术的兴趣，这直接导致了大四年级数学师范普遍实习归来后其TPACK有所降低．

（3）数学师范生所具备的TPACK存在年级差异的另一个原因可能为5个影响因素对不同年级数学师范生TPACK的影响强度不尽相同．5个影响因素对数学师范生TPACK的影响强度均在大一或大二年级最高，其中教师职业认同、动机和自我效能感、教学实践经历3个因素对大一年级数学师范生TPACK的影响最大，教育技术课程、学校资源与环境两个因素对大二年级数学师范生TPACK的影响最大．由此表明，自身心理状况与教学实践经历在数学师范生的早期培养阶段有巨大作用，而外部条件及教育技术课程在数学师范生的中期培养阶段有巨大作用．

综上所述，青海省高校应该对数学师范生在各个培养阶段进行针对性的培养以得到其TPACK的最大发展．例如，在数学师范生的早期培养阶段应为学生多组织教师从业思想教育活动、多安排教育见习活动，增加数学师范生的职业认同与自我效能感，更加坚定其成为一名教师的决心；在数学师范生的中期培养阶段应为学生开设教育技术相关课程，并提供配套的设施资源、辅以定期的教育实习以便学生巩固课堂学习的知识，及时通过实践发现课堂学习中遗漏的问题，以便查漏补缺；在数学师范生的后期培养阶段应加大社会资源的投入，各中小学校或有关教育部门应对教师提供足够的教育技术培训机会，使脱离师范院校培养后的教师能够继续学习新的教育技术，各学校也应鼓励教师使用现代教学设备，让教师在教学中能够发挥自己的技术知识，让技术有用武之地．

[1] 解书，马云鹏，李秀玲．国外学科教学知识内涵研究的分析与思考[J]．外国教育研究，2013，40（6）：59-68．

[2] 左敬亮，方勤华，程垚松．美国“数学教师TPACK标准和发展模型”——数学教师有效使用技术的新焦点[J]．数学教育学报，2016，25（2）：44-48．

[3] Shulman L. Those who understand: Knowledge growth in teaching [J]. Educational Researcher, 1986 (15): 4-14.

[4] Shulman L. Knowledge and teaching: Foundations of the new reform Harvard educational [J]. Review, 1987, 57 (1): 1-22.

[5] Graeber A O. Forms of knowing mathematics: What preservice teachers should learn [J]. Educational Studies in Mathematics, 1999 (38): 189-208.

[6] Koehler M J, MISHRA P. What happens when teachers design educational technology? The development of technological pedagogical content knowledge [J]. Journal of Educational Computing Research, 2005, 32 (2): 131-152.

[7] Mishra R, Koehler M. Technological pedagogical content knowledge: A framework for teacher knowledge [J]. The Teachers College Record, 2006, 108 (6): 1 017-1 054.

[8] Koehler M J, Mishra P. Introducing TPACK [M] // AACTE Committee on Innovation and Technology. Handbook of technological pedagogical content knowledge (TPCK) for educators. New York: Routledge, 2008: 3-4.

[9] 袁智强．整合技术的学科教学知识研究综述[J]．数学教育学报，2012，21（6）：13-18．

[10] 杨宝忠，孟晶．小学数学新教师TPACK现状——以天津市某区为例[J]．数学教育学报，2018，27（4）：53-57．

[11] 张新颜．初中数学教师TPACK结构的探索研究[J]．数学教育学报，2016，25（4）：79-83．

[12] 中华人民共和国教育部．教育信息化十年发展规划（2011—2020年）[M]．北京：人民教育出版社，2012：29.

[13] 徐鹏．教师整合技术的学科教学知识影响因素模型构建研究[D]．长春：东北师范大学，2014：11．

[14] 朱建平，殷瑞飞．SPSS在统计分析中的应用[M]．北京：清华大学出版社，2007：20-28．

[15] 吴明隆．结构方程模型——AMOS的操作与应用[M]．重庆：重庆大学出版社，2018：45-49．

[16] 余晓娟，林子植．结构方程模型在数学教育研究中的应用[J]．教育测量与评价，2019（4）：18-24．

[17] 聂晓颖．数学师范生整合技术的学科教学知识影响因素分析与培养模型研究[D]．西安：陕西师范大学，2017：26-28．

Analysis of the Grade Difference of TPACK of Mathematician in Local Colleges and Universities: Take Qinghai Province as an Example

WANG Yu, KONG Ling-yu, GUO Cheng-yu

(College of Mathematics and Statistics, Qinghai Normal University, Qinghai Xining 810008, China)

TPACK is called the technological pedagogical content knowledge. It is the basis of effective teaching in today’s era and an important key content of the professional development of teachers. Therefore, the TPACK mastery of mathematics teachers in local colleges has a direct effect on the quality of future mathematics teaching in the region. The mastery of TPACK is often affected by many factors such as the educator’s own psychological or external conditions. This study takes into account the factors affecting the mastery of TPACK, and constructs the “Mathematics Teacher TPACK Questionnaire” to conduct a full sample survey of mathematics teachers in Qinghai Province. Through statistical analysis of survey data, we learned that there are significant grade differences in CK, PK, PCK, TCK, TPK, and TPCK possessed by mathematics teachers in Qinghai university; the influencing factors have different influences on the TPACK of different grade mathematicians. Finally, this study proposes suggestions for the development of TPACK for normal university in different grades according to the different influence intensity of each influencing factor on TPACK for mathematics students in different grades.

local universities; mathematics normal students; TPACK; grade difference

G645

A

1004-9894（2021）03-0090-06

王煜，孔令钰，郭承育．地方院校数学师范生TPACK的年级差异性分析——以青海省为例[J]．数学教育学报，2021，30（3）：90-95．

2021-04-21

国家社会学科基金“十三五”规划2019年度教育学西部项目——青海少数民族地区中学理科教师胜任力研究（XHA190294）

王煜（1964—），男，陕西宝鸡人，教授，主要从事数学课程与教学论研究．郭承育为本文通讯作者.

[责任编校：陈隽、陈汉君]