预设的学习轨迹转化为课堂实践的课例研究——以相等分数为例

黄兴丰，黄荣金

预设的学习轨迹转化为课堂实践的课例研究——以相等分数为例

黄兴丰1，黄荣金2

（1．上海师范大学 国际与比较教育研究院，上海 200234；2．中田纳西州立大学 数学系，美国 田纳西州）

理论到实践的转化一直是教育领域努力探索的问题．课例研究被认为是解决这一问题的有效途径．以跨界学习中的边界对象作为分析工具，通过边界对象的生成和变化，展现预设的学习轨迹转化为课堂实践的历程．研究发现：（1）研究课是预设的学习轨迹转化为课堂实践的有效动力；（2）跨越边界的中介者（教师、研究者）是实现转化的关键要素；（3）关注学生的学习是理论转化为实践的主要目标．

课例研究；理论到实践；跨界学习；预设的学习轨迹

理论联系实践是教育中长期探索的问题，许多研究揭示了二者割裂的多种原因，同时也提出了解决这一矛盾的不同方法[1-3]．特别是，布莱克（Bryk）等把医疗中“改进的科学”（improvement science）引入教育领域，通过计划（plan）、实施（do）、研究（study）、改进（act）4个阶段不断反复循环，促进理论在实践中的应用[4]．改进的科学改变了人们对研究和实践的认识，强调了人们所处情境的重要性．研究者与实践者应当在差异中获取信息资源，在实践中分享知识和智慧，重新设计解决问题的方法[5]．为了实现研究、理论对改进教育实践的目的，莫里斯（Morris）和希伯特（Hiebert）指出，当前可能解决困境的办法是创造一种“可分享并且能灵活应用的知识”，指导和改进实践[6]．蔡金法等指出，改进的科学是实现教育理论向实践转化的重要范式，研究者应该根据教师的需求，生成假设、检验假设、分析结果、改进实践[7]．盛行于亚洲国家，以中国和日本为主的课例研究（lesson study）作为一种教师合作专业发展的模式，根植于教师工作场景，已有一百多年的历史[8-9]，具有“改进的科学”的基本特征[10]．因此，课例研究可以为研究者和实践者发展理论和改进实践提供一个有效的途径．

尽管不少学者探索了中国课例研究在理论联系实际中所起的作用[11-14]，但是，从理论到实践的转化机制还是一个灰箱，被人知之甚少．这里试图以小学数学相等分数的学习轨迹（learning trajectory）作为课堂教学的指导理论，借助实践共同体及边界对象（boundary object）作为分析工具[15]，剖析理论到实践的转化过程．

1 理论框架和文献

1.1 课例研究与教师学习

课例研究是一种嵌入工作场景，浸润于实践，聚焦学生学习的专业发展模式[16]，一般包含研究（study）、计划（plan）、教学（do）和反思（reflect）4个环节[17-18]．作为教师专业发展的一种有效途径，课例研究逐渐风靡全球．许多研究表明课例研究可以产生多方面的价值，包括提高课堂教学水平，促进教师和学生的学习，推动新课程的实施，在理论与实践之间建立纽带[19-20]．课例研究通过构建教师实践共同体，为教师与研究者创造了互动合作的环境，能引发教师在个人观点与研究理论间产生共鸣，激发他们共同协作寻找解决问题的动力，最终促进理论向实践转化[21]．

1.2 作为实践共同体的课例研究

社会文化视角下的实践共同体，为研究者提供了在课例研究中分析理论到实践转化的理论基础．根据温格（Wenger）的观点，教师学习是在实践共同体中通过与其他成员合作而实现的[15]．温格认为实践共同体有3个关键要素：第一要有相互的投入，共同体的成员之间要产生互动和合作，而且教师能在这种互动和合作中共享知识和经验（例如，共同设计教学，一起观察课堂，集体评价）；第二要具备共同的事业，能激励教师为了共同的目标而努力，主动贡献各自的经验（例如，通过课例研究，重新定位学生的学习目标）；第三要有可共享的资源库，共同体应当拥有共同的资源，便于相互协商、讨论和学习（例如，对课例研究、有效教学达成的共识）．

在研究者和教师共同合作的过程中，课例研究创造了两个跨界的共同体（教师、教师教育工作者），边界一方面给不同共同体之间的学习带来了障碍，但另一方面也为他们的学习带来了机会．教师一旦跨越边界就可以看到“墙外另一个不同的世界”．因此，跨界学习是研究者和教师在课例研究中，实现理论与实践融合的关键．其中，跨界学习的发生依赖两个重要的载体：边界对象（boundary objects）和中介者（broker）[15]．边界对象是凝聚了两个或多个共同体理念观点的载体．在课例研究中存在多种形式，比如，具体的教学活动、教学设计的文本材料、研究课、学生学习文档（如解答）等．这些具体形式，必须是两个或多个共同体成员共同形成的，否则就不是边界对象．中介者是试图跨越边界的个体．他们穿梭在不同共同体之间，以边界对象为具体载体，传递和分享知识．因此，边界对象的形成、变化和发展离不开中介者的跨界努力．

然而，跨界学习的程度可能是不一样的，会出现3个不同的水平：协调（coordination）、透明（transparency）和协商（negotiability）[22]．协调就是来自某个共同体的参与者按照来自其他共同体成员的要求和规则“做什么”，这时，他们可能不知道“为什么”要这么做，因此这些参与者的投入是被动的．透明则比协调更进一步，参与者不仅知道做什么，而且还知道“做什么”背后的意义和原理，因此他们就有可能把这些做法迁移到新的情境中去．不过，他们的参与与其他共同体的成员相比还是不平等的，尚处于指导和被指导的关系．协商则是指来自不同共同体的成员，他们之间的关系是平等的，各方通过积极主动的参与，同时在与边界对象的相互作用下获得意义体验，并由此增强个体体验新意义的能力．从这3个水平的跨界学习来看，协商的跨界学习才能真正体现不同共同体成员之间的平等、主动和积极性．因此，协商的跨界学习，应当是实践共同体所有成员始终追求的目标和努力的方向．

研究者通过和教师共同参与课例研究，尝试把学习轨迹的理论观点应用于课堂教学，探索课例研究作为实践共同体实现理论到实践转化的内在机制．为了清楚地表达研究的设想，研究者构建了直观的模型（图1）来说明研究的基本假设．（1）在课例研究中，为了实现从理论到实践的转化，边界对象成为研究者和教师实现跨界学习的重要载体．在课例研究过程中，研究者和教师以研究课作为载体，通过双向的意义沟通，视角和身份的转换，促进跨界协商的发生和形成．在此过程中，不同成员达成的共识逐渐成为联结不同共同体的边界对象．而且，处于理念状态的共识，还可以转化为具体的计划和实践的课堂，这就是逐渐“物化”的过程，也就是理论转化为实践的过程．如果研究者和教师就某个观点或方案无法达成一致意见，也就是说，他们无法形成跨越共同体的边界对象，那么也就意味着很难实现从理论到实践的转化．（2）在课例研究的过程中，研究者与实践者之间的跨界学习可能发生在共同体成员讨论教学设计、课堂实施，以及教后的集体反思之中，由此通过循环反复实现从理论到实践的转化．

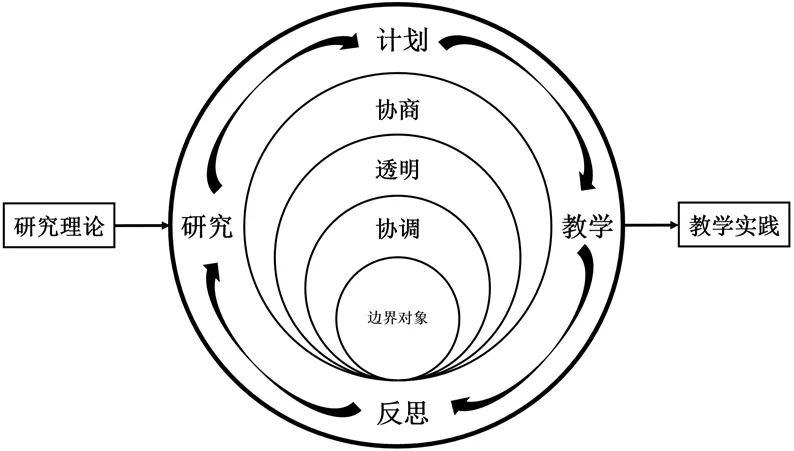
图1 在课例研究中从理论到实践转化的分析框架

1.3 学习轨迹理论视角下的数学教学

自从西蒙（Simon）[23]和其他学者[24-25]提出了学习轨迹的概念之后．很多研究表明，学习轨迹可以促进教师的知识发展，有助于教师在课堂中做出合理的教学决策，能帮助教师理解并把握学生的思维发展[26-30]．根据西蒙的定义，预设的学习轨迹是学生在向预定目标推进中经过的路径，它有3个组成要素：学习目标、学习活动和学习过程．研究人员结合具体数学内容和相关研究结论，就可以建立起预设的学习轨迹[23]．

相等分数是理解分数运算、分数和小数关系的重要基础．相等分数的理解包括两个方面：第一，形式不同的分数可以表示相同的数量；第二，相等分数之间，分子和分母蕴含确定的数量关系．为了促进儿童对相等分数的理解，研究者发展了形象（figurative）和操作（operative）这两种教学方法[31]．形象教学法关注分数表示的对象看起来是否相同（如相同的长度或面积），但很难帮助儿童理解分数之间的关系．操作教学法关注如何对一个分数进行操作（例如，一根小木棒是原来整体的3/4．如果再把每份等分成2份，那么这根木棒可以看成是整体的6/8），从而理解相等分数之间的等价关系．这两种方法都兼容了“部分与整体”的解释（例如，/是指，把1个整体平均分成份，取其中份）和“测量”的解释（/是指，用分数单位1/重复测量次）．形象教学法是数学教材最常见的方法，其通常的步骤是：

（1）使用图形、数线、实物，帮助儿童理解为什么两个分数相等；（2）在相等分数之间寻找规律；（3）最后生成算法（分子和分母相乘或相除同一个非零数）[32-34]．然而，研究者认为，这种经验方式建立起来的相等分数概念，并不能帮助儿童理解相等的逻辑必然性．相比而言，操作教学法却可以帮助儿童真正理解等量分数之间的关系[31]．

对于相等分数，上海课程在四年级预设的学习轨迹只要求学生能在不同的直观模型中用相等分数表示相同的对象，并不要求学生能解释分数的等价性，直到六年级才要求学生能解释相等分数的意义[35]．然而，不同课程对于相等分数预设的学习轨迹并不完全一致．比如，在“美国州际数学共同核心标准”中[36]，明确要求四年级学生不仅能在直观模型中用相等分数表示相同的对象，而且还要求学生能解释相等分数的意义．结合上述研究和文献，研究者预设了相等分数的学习轨迹（表1）．相对于上海数学课程而言，增加了L2这个子目标，这自然成为课例研究的焦点．或者说，预设的学习轨迹应当成为联结研究者和教师两个共同体的边界对象，即通过课例研究，以预设的学习轨迹作为引领课堂教学的理论．

因此，研究的具体问题是：在课例研究中，预设的学习轨迹如何成为联结研究者和教师两个共同体的边界对象？预设的学习轨迹在成为边界对象的过程中受到了哪些因素的影响？

2 研究方法

课例研究的团队成员包括1名大学研究者（第一作者）和来自7所小学（一年级到五年级）、2所初中（六年级到九年级）的12名教师．他们都来自中英数学教师交流项目组．课例研究最主要的目的是为了形成一节展示课，与远道而来的英国教师共同探讨上海数学教学的重要特征．这些教师来自上海黄浦、静安、徐汇、浦东、虹口、闵行6个区，所在学校都是各区享有较高知名度的学校．大学研究者（第一作者）来自上海的一所师范大学，多年从事中小学数学教学和研究，并协助单位领导具体实施中英数学教师交流项目．执教的王老师，来自上海浦东一所城郊小学，已有6年的教学经历．她目前承担了4年级两个班的数学教学，同时还负责组织所在年级的数学教研活动，曾多次参加中英数学教师交流，是一位优秀的年轻教师．事实上，在此研究团队中，由于研究者和教师工作性质的不同（研究者侧重理论研究，教师注重课堂实践），因此可以把他们看成是来自不同实践共同体的成员．在课例研究的过程中，他们分别承担了不同的角色和责任（表2）．

如表2所示，课例研究一共进行了4次集体活动（包括课堂教学和集体研讨），目的是尝试把预设的学习轨迹中的L2子目标转化为课堂实践，形成将来可以展示的课堂教学设计．每次集体活动都进行了全程录像，4名研究助手将录像中的音频转录为文本，用于数据的分析．根据研究的问题，教师在跨界学习中出现的关键变化成为分析的焦点．随后，研究者针对这些变化对教师进行了半开放访谈，寻找引起这些变化的可能原因．

表1 预设的相等分数学习轨迹

表2 课例研究的过程及活动内容

3 研究结果

3.1 理念中的学习轨迹：矛盾与协调

在第一次研究讨论中，不少教师表示，在小学阶段如果要求学生借助直观模型来解释相等分数，可能会超出他们的认知水平．不过，研究者指出，美国数学州际共同核心标准明确要求四年级学生能借助直观模型解释相等分数的意义．研究者向教师介绍了预设的学习轨迹，希望从学习轨迹的视角改进课堂教学．于是，研究者提出了一个新的教学目标（预设的学习轨迹中的L2）：能否在分数单位的基础上，构造新的分数单位，并以此来表示原来的分数？比如，三等分一个圆，得到分数单位1/3，然后再等分这个1/3，就可以得到一个新的分数单位1/6，原来的1/3就变成了2个1/6，就是2/6．部分教师的态度开始出现转变，王老师愿意尝试这样的教学活动．于是，预设的学习轨迹开始成为两个共同体的边界对象．

为了了解这个活动的可行性，研究者和教师在第一次活动结束后设计问题对学生进行课前测试：（1）请学生借助部分与整体的直观模型写出不同的分数表示指定的量；（2）请学生利用表示单位1的图形，在已有分数单位1/2的图形上，通过等分生成新的分数单位1/4、1/6的图形．结果发现在一个班超过90%的学生都能完成这两类问题的解答．调查的结果不仅增强了研究者和教师的信心，而且更多教师开始认同和接纳这个预设的学习轨迹．

3.2 设计中的学习轨迹：设想与透明

王老师在教学设计中，采用了研究者预设的教学活动．她在第二次会议讨论中讲述了她的教学设计．

王老师：……我请找到八分之四的同学来分享方法．在四分之二的基础上，再折一次，然后进行比较．我会问，现在每一份是多少？是八分之一．追问：八是怎么来的？原来一共有四份，每一份再平均分为二份，四乘二等于八．我会问这里的八怎么来的，就是原来四份，每份都分成二份了．现在涂色部分占几份？四份．那四是怎么来的？原来涂色部分是二份，每一份再平均分成二份，二乘二等于四．把每一个再平均分成二份．接下去，我会把四分之二对应的图，每一份再分成三份，得到的份数是什么？和原来的分数还相等吗？分为四份、五份、六份呢？还和原来相等吗？

除了3个教师外，所有的参与者都基本认可王老师的设计，同时也提出了进一步改进的建议．特别是在请学生解释的时候，他们建议要借助具体图形，不能只借助语言，否则太抽象，学生不容易理解．有3个教师提出了质疑或反对．

陈老师的顾虑主要来自于她个人的教学经历．

陈老师：小学阶段不用出现分子分母同时扩大的解释．只要让学生感觉到，分数单位不同，要保持分数大小相等的话，对应的分子也要随着改变．我觉得理解到这一层，就达到了教学目标．我在过去的教学中，只有一次发现一个同学会这样解释，而且这个是很好的学生．

陆老师的顾虑可能是受到了教材设计的影响．

陆老师：我们现在四年级，不能出现这句话“分子分母同时乘或除以……”，我们鼓励学生去发现，我们不要讲得太多．你说的话，学生一定懂的，但是这个问题还是应该留到六年级．到时候，借助图形，他就明白了．现在四年级的孩子，就是感受一下．

顾老师还是怀疑学生是否有能力在分数单位的基础上生成新的分数单位．

顾老师：把一张纸折成四份，二分之一就是二个四分之一，我觉得这个没问题．但是小朋友得到这块是四分之一，还是四份当中的一份，他不会从“二分之一的一半是四分之一”来考虑．

从以上教师反馈可以看到，教师仍可能不愿意尝试新的教学活动．尽管前面测试结果表明学生有能力在直观模型中找到相等分数，也能通过等分构造新的分数单位，但是教材以及教师以往的知识经验对边界对象的形成造成了障碍．

王老师之所以能很快进入跨界学习的状态，与她和研究者多次的交流有关．她在访谈中解释说，因为课例研究在她的学校开展，所以她和研究者共同承担了组织和协调的工作．同时研究者也经常和她通过电话或网络进行非正式的讨论．这使她比其他教师更有机会了解研究者的意图和研究的目的．同时，她还帮助调查了学生的数学学习情况，整理和分析了学生的测试结果．这使得她更有信心来尝试这样的做法．

另外，王老师也谈到了她过去的一次经历．她曾经去外地参加过一个课堂观摩活动，看到了执教教师在课上使用分数单位生成分数的情形．由此，她更深刻地认识到了分数单位的重要意义，“其地位就如同整数中的单位1”．于是，当研究者提到分数单位的时候，一下子唤醒了她对过去这段经历的记忆．也就是说，她和研究者的协作和沟通，以及她对所教知识的理解和认识，使新的教学活动对她而言变得更加透明，也成为她愿意尝试跨界学习的一个动力．

3.3 课堂中的学习轨迹：实践与协商

王老师设计的第一个教学任务来自于教材，借助直观图形从部分与整体出发，用相等分数表示图形中指定的部分．她先请学生猜一猜两个分数的大小，然后要求学生通过折纸操作，验证自己的猜想．

在第二个教学任务中，王老师利用直观图形，在已有分数单位的基础上，请学生再构造新的分数单位，由此建立两个分数之间的相等关系．在教学中，她强调了学生解释分数相等的原因．在开始的时候，学生的解释还并不流畅，但是在教师利用了指导性的语言（把图中的每一份再平均分成份，每一份变为，红色部分变为份，就是个，是）反复练习之后，学生的口头解释变得越来越流利，学生还可以由此来构造更加复杂的相等分数，并能解释其中的原因．

［王老师第一次教学中的片段］

师：现在你还能找到和四分之一相等的分数吗？

生：每一份平均分成六份，每一份变为二十四分之一，红色部分变为六份，就是六个二十四分之一，就是二十四分之六．

师：谁再来说一说？

生：每一份平均分成十份，每一份变为四十分之一，红色部分变为四十分之十．

师：我来问一个，你把每一个部分分成十份，四十哪来的？

生：四乘十是四十．

师：谁再来说一个，每一个平均分为几份？

生：每一份平均分为五份，每一份变为二十分之一，红色部分变为五份，就是五个二十分之一，是二十分之五．

在讨论的过程中，出乎意料的是不再有教师质疑新的教学活动．大家讨论的话题全部转向如何有效地实施教学过程．与前面相比，尽管研究者多次向教师解释和讨论相关的理论和研究，然而对于部分教师而言，边界对象还不透明，研究者和这些实践者之间很难达到跨界协商的水平．但是当他们看到王老师的课堂具体实施之后，参与教师的态度出现了明显的转变．

先前持反对态度的陆老师解释说，在教学设计的讨论过程中的“反对”和“质疑”，主要是研究者和教师所处的立场不同．

陆老师：研究者通常在现有的教学理论背景下，依据研究的结论提出相应教学活动；而我们作为实践者注重的是对学情分析，习惯从课堂实际出发确定教学方法．因此两者之间的跨界协商必然不易达成．

同样，前面有所顾虑的顾老师也表达了类似的观点．

顾老师：研究者站在更高更理论的角度看待问题，但是我们考虑的总是具体的问题，比如，怎么帮助不同能力的学生等．

王老师实施的课堂，尽管在教学设计的阶段，有少数教师持不同的观点，但是不管如何，实施的课堂作为一个已经完成的对象，是研究者和教师群体参与协商物化学习轨迹的结果．因此，在教学设计之后，研究课成为学习轨迹物化的边界对象，帮助那些徘徊在共同体边缘的教师迈出了跨界学习的第一步，理论和实践在课堂中得到了联结．

陆老师：之所以出现这样的转化，是因为我们作为实践者想达到的教学效果与研究者预设的教学活动没有背离．我觉得我们彼此处于一段平行后产生了交点．

顾老师觉得这正是课例研究的魅力，可以借鉴他人课堂的成功之处，改进自己的教学．

缪老师则更加明确地谈到了作为课堂对于教师专业发展的重要意义．

缪老师：我觉得研究者更多的是从理论的层面，为我们解释相关研究．对于我们一线教师而言，没有亲身经过实践的理论听起来是模糊的．具体应该怎么做？如何落实在课堂？这些我们都会有疑问．因此大道理说再多，不如动手去做一做．当王老师把理论融于课堂后，我们实实在在地看到了具体的落实过程，所以大家之前的反对或质疑都消失了．

从教师的反馈来看，课堂作为学习轨迹物化的边界对象（观摩和研究的对象）可以更有效地协调不同的视角，使那些边缘参与[37]的教师积极参与意义协商的互动过程．

尽管如此，研究者和大部分教师都感觉王老师在第二个任务的实施过程中，反复操练的痕迹太重，教师控制得太多．王老师后来告诉研究者当时她的顾虑．

王老师：用分数单位解释相等分数是我在之前的教学中没有尝试过的．但我和其他老师一样，我也有顾虑学生是否能够说清楚分数相等的本质．因为我担心学生不会说，我就提供了指导性的语言．我又怕学生不理解，于是就讲了平均分成二份、三份、四份等情况．刚开始时，指导性语言确实能帮助学生，但是到了后面，指导性语言反而会约束学生的思维和表达．

在第二次教学中，她接受了大家的建议，减少了第二个教学任务中的内容，同时也减少了对学生的控制．在课堂中学生运用自己的语言来表达他们对相等分数的理解，实现了大家期望中的课堂．

在王老师看来，二次教学让她更加了解学生的学习困难，共同体内教师的建议让她获得了不同视角的反馈，使她能更准地拿捏教学的重点．

王老师：二次教学过程，以及其他老师的建议和反馈，让我能更加了解学生的困难，这对我调整教学起到了关键的作用．同时，也启发我在今后的教学中应当多角度地思考学生可能存在的困难．

顾老师也表达了类似的观点，认为二次教学可以促进执教者的专业成长．

顾老师：对不同的学生上同样的内容，可以锻炼教师“备学生”的能力，能帮教师更好地了解学生．不同教师对于同一课的研究，可以帮助教师打开思路，从不同角度思考问题．

也就是说，两次教学可以使研究课中的学习轨迹，成为共同体持续协商的边界对象，在此过程中执教者可以对边界对象获得新的意义体验，可以增强他们体验新意义（跨界学习）的能力．

在缪教师看来，二次教学也让她获得了新的体验．

缪老师：多次教同一节内容的课，大家在参与讨论中才会对课有深刻的认识和理解，才能把同一内容挖得深、想得远．每次执教都是不同的学生，参与讨论的老师就能看到同一内容在不同学生群体中执教的效果，有助于大家反思和改进教学活动．

在此过程中，预设的学习轨迹，以物化为课堂实践的方式，在多次实践中，成为不断具体化的边界对象．

4 讨论与启发

研究展现了预设的相等分数的学习轨迹转化为课堂实践的过程．首先，研究者预设的学习轨迹，一开始只是引发了部分教师的兴趣和认同，成为最初的边界对象．尽管研究者随后又为教师提供了来自学生的调查数据，但还是有教师质疑课堂实施的可行性．随后，王老师欣然成为积极的跨界者．学生在课堂中的表现促进了参与教师认知的根本转变．学习的轨迹物化为课堂实践，成为有效的边界对象，调和了两个共同体之间的不同观点，初步实现了理论向实践的转化．最后，学习的轨迹继续物化为改进的课堂实践，成为共同体持续协商意义的资源．教师不断“卷入”其中，获得新的意义体验．也就是说，教师通过跨界学习，实现理论向实践的转化．

对理论转化为实践的启发在于：首先，研究者要引入与学生学习密切相关的、具有潜在作用的理论（如相等分数的学习轨迹），以解决教师所关注的实际问题（如理解相等分数）．例如，理论的选择要与学生的学习密切相关，教学任务的选择要根据理论进行设计．第二，教师通过合作设计并尝试课堂教学．在课例研究中，教师集体性的合作、参与和反思是不可或缺的．第三，根据学生在课堂教学中的表现，对学生的学习效果进行合理评价．课例研究小组（包括教师和其他参与者）应当集体分析课堂的实施情况，找到改进教学的方法，促进教师的专业发展．第四，修改设计，再次对其他学生实施相同内容的课堂教学，让改进的教学在实际课堂中发挥更好的作用，同时鼓励发现新问题，激发教师围绕新问题，继续新的课例研究．

从实践共同体的视角来看，研究者和教师两个共同体的跨界是实现理论到实践转化的关键．教师作为跨越共同体的中介者是不可或缺的关键要素．比如，王老师作为跨越边界的中介者发挥了极其重要的作用．她从研究者那里带回关于相等分数预设的学习轨迹，应用于自己的教学设计和课堂，促进了从理论到实践的转化，进而影响和改变了其他教师的观念．像王老师那样率先尝试跨界的教师，被索德（Sowder）等称为“教师领导者”[38]．在理论转化为实践的过程中，教师领导者扮演了中介者的角色，起到了关键性的作用．他们不仅拥有丰富的知识和经验，更重要的是他们愿意接受新的理论改进自己的教学．

就研究者而言，他们与教师看待问题的视角存在文化的差异．一般说来，研究者为了解决实践中存在的问题，不得不深入学校和课堂开展实验性研究．然而，教师却不太情愿把精力和时间花费在这些尚无定论的方法上．因此，对研究者而言要想让教师相信和认同研究的成果并运用于实践，绝不是一件简单的事情．为了实现理论向实践的转化，研究者除了要学会倾听教师的心声，尊重教师的意见之外，更重要的是，要能比较全面地把握已有研究的进展和尚且存在的不足，要善于从实践者的角度来思考理论的合理性和可行性．比如，在相等分数的课例研究中，一方面，研究者不仅要了解国内课程的要求，不同教材预设的学习轨迹，而且要了解国内外关于相等分数教学研究的进展和局限，不同文化环境中的教学差异．另一方面，研究者还要勇于转变自己的角色和身份，从教师的立场来思考教学的实施，思考已有研究所预设的学习轨迹是否契合中国学生的具体实际．

致谢：感谢上海市浦东新区御桥小学以及参与此研究的各位老师给予的大力支持．同时感谢北京大学陈向明教授对文章提出的宝贵意见．

[1] CAI J, MORRIS A, HWANG S, et al. Improving the impact of educational research [J]. Journal for Research in Mathematics Education, 2017, 48 (1): 2-6.

[2]KIERAN C, KRAINER K, SHAUGHNESSY J M. Linking research to practice: Teachers as key stakeholders in mathematics education research [M]. NewYork: Third International Handbook of Mathematics Education, 2013: 361-392.

[3]SILVER E, LUNSFORD C. Compendium for research in mathematics education: Linking research and practices in mathematics education: Perspectives and pathways [M]. Reston: National Council of Mathematics Teachers, 2017: 28-47.

[4]BRYK A, GOMEZ L, LEMAHIEU P. Learning to improve: How America’s school can get better at getting better [M]. Cambridge: Harvard Education Press, 2016: 1-20.

[5]LEWIS C. What is improvement science? Do we need it in education? [J]. Educational Researcher, 2015, 44 (1): 54-61.

[6]MORRIS A K, HIEBERT J. Creating shared instructional products: An alternative approach to improving teaching [J]. Educational Researcher, 2011, 40 (1): 5-14.

[7]CAI J, MORRIS A, HWANG S, et al. Clarifying the impact of educational research on learning opportunities [J]. Journal for Research in Mathematics Education, 2017, 48 (3): 230-236.

[8]LEWIS C, TSUCHIDA I. A lesson is like a swiftly flowing river: How research lessons improve Japanese education [M]. American Educator, 1999, 2 (1): 48-56.

[9]LI X. Theory and practices of lesson study in mathematics: An international perspective: An analysis of Chinese lesson study from historical and cultural perspective [M]. New York: Springer, 2019: 201-228.

[10]HUANG R, FANG Y, CHEN X. Chinese lesson study: An improvement science, a deliberate practice, and a research methodology [J]. International Journal for Lesson and Learning Studies, 2017, 6 (4): 270-282.

[11]杨玉东．课例研究的国际动向与启示[J]．全球教育展望，2007，36（3）：47-49．

[12]HUANG X, HUANG R, HUANG Y, et al. Theory and practice of lesson study in mathematics: Lesson study and its role in the implementation of curriculum reform in China [M]. Cham: Springer, 2019: 229-252.

[13]HUANG R, GONG Z, HAN X. Implementing mathematics teaching that promotes students’ understanding through theory-driven lesson study [J]. ZDM Mathematics Education, 2016 (48): 425-439.

[14]DING L, JONES K, SIKKO S. Interconnectedness and difference between action research and a lesson design study in Shanghai, China [J]. Educational Action Research, 2020, 27 (4): 595-612.

[15]温格．实践共同体：学习、意义和身份[M]．李茂荣，欧阳忠明，任鑫，等译．南昌：江西人民出版社，2018：67-79，96-113.

[16]MURATA A. Introduction: Conceptual overview of lesson study [M] // HART L C, ALSTON A S, MURATA A. Lesson study research and practice in mathematics education. Springer, 2011: 27-39.

[17]LEWIS C. How does lesson study improve mathematics instruction [J]. ZDM Mathematics Education, 2016, 48 (4): 571-580.

[18]LEWIS C, PERRY R, HURD J. Improving mathematics instruction through lesson study: A theoretical model and North American case [J]. Journal of Mathematics Teacher Education, 2009 (12): 285-304.

[19]XU H, PEDDER D. Lesson study: Professional learning for our time: An international review of the research [M]. London and New York, NY: Routledge, 2014: 29-58.

[20]HUANG R, SHIMIZU Y. Improving teaching, developing teachers and teacher developers, and linking theory and practice through lesson study in mathematics: An international perspective [J]. ZDM Mathematics Education, 2016, 48 (4): 393-409.

[21]RUNESSON U, THORSTEN A. How teachers’ practice knowledge is used and challenged in a learning study using variation research as a tool [J]. International Journal for Lesson and Learning Studies, 2015, 4 (3): 274-287.

[22] WENGER E. Conceptual tools for CoPs as social learning systems: Boundaries, identity, trajectories and participation [M] // BLACKMORE C. Social learning systems and communities of practice. London: Springer, 2010: 125-143.

[23]SIMON M. Prospective elementary teachers’ knowledge of division [J]. Journal for Research in Mathematics Education, 1993, 24 (3): 233-254.

[24]CLEMENTS D H, SARAMA J. Learning trajectories in mathematics education [J]. Mathematical Thinking and Learning, 2004, 6 (2): 81-89.

[25]SZTAJN P, CONFREY J, WILSON P H, et al. Learning trajectory based instruction: Toward a theory of thinking [J]. Educational Researcher, 2012, 41 (5): 147-156.

[26]CLEMENTS D, SARAMA J, SPITLER M, et al. Mathematics learned by young children in an intervention based on learning trajectories: A large-scale cluster randomized trial [J]. Journal for Research in Mathematics Education, 2011, 42 (2): 127-166.

[27]WILSON P H, SZTAJN P, EDGINGTON C, et al. Teachers’ uses of a learning trajectory in student-centered instructional practices [J]. Journal of Teacher Education, 2015, 66 (3): 227-244.

[28] 何声清．“代表性启发”对初中生古典概率内容学习进阶的影响[J]．数学教育学报，2020，29（4）：27-33．

[29] 李化侠．学习进阶视角下小学生统计思维发展水平研究[J]．数学教育学报，2019，28（6）：55-60．

[30] 吴颖康，邓少博，杨洁．数学教育中学习进阶的研究进展及启示[J]．数学教育学报，2017，26（6）：40-46．

[31] KARA M, SIMON M, PLACA N. An empirically-based trajectory for fostering abstraction of equivalent-fraction concepts: A study of the learning through activity research program [J]. Journal of Mathematical Behavior, 2018 (52): 134-150.

[32] FUJII T, IITAKA S. Mathematics international Grade 4 [M]. Tokyo: Tokyo Shoseki, 2012: 40-50.

[33] ASKEY R, JACKSON B, KEMPE J. Primary mathematics: Teacher’s guide 3B [M]. Singapore: Marshall Cavendish Education, 2014: 20-30.

[34] 邱万作，黄华．初中数学课本六年级（上）[M]．上海：上海教育出版社，2018：27-39．

[35] 上海市教育委员会．上海市中小学数学课程标准[M]．上海：上海教育出版社，2006：41-52.

[36]全美州长协会和首席州立学校官员理事会．美国州际核心数学课程标准：历史、内容和实施[M]．蔡金法，孙伟，译．北京：人民教育出版社，2016：27-32．

[37] 莱夫，温格．情境学习：合法的边缘性参与[M]．王文静，译．上海：华东师范大学出版社，2004：1-11．

[38] SOWDER J, BARNES D, HAGELBERGER B, et al. Harnessing the power of research for practice [R]. National Council of Teachers of Mathematics Board, 2005.

Transition from a Hypothetical Learning Trajectory to Classroom Practice through Lesson Study: A Case of Teaching Equivalent Fractions

HUANG Xing-feng1, HUANG Rong-jin2

(1. Research Institute for International and Comparative Education, Shanghai Normal University, Shanghai 200234, China;2. Department of Mathematical Sciences, Middle Tennessee State University, Tennessee, USA)

Linking theory to practice is a long-standing unsolved issue in the field of education. Lesson study is considered to be an effective way to address this problem. This study used the boundary objects in boundary crossing learning as an analytical tool to show how a learning trajectory can be utilized to improve classroom practice through the generation and refinement of boundary objects. The study indicated that: (1) Implementing research-oriented classroom teaching is an effective driving force to promote the transition from theory to practice; (2) brokers (teachers, researchers) across the boundary are the key elements to make the transition; and (3) attention to students’ learning is the most important goal of making the transition from theory to practice.

lesson study; theory to practice; learning cross-boundary; hypothetical learning trajectory

G40-03

A

1004-9894（2021）03-0025-07

黄兴丰，黄荣金．预设的学习轨迹转化为课堂实践的课例研究——以相等分数为例[J]．数学教育学报，2021，30（3）：25-31．

2021-05-06

全国教育科学“十三五”规划2018年度国家一般课题——中学生合作问题解决中认知互动与社会互动及其关系的实证研究（BHA 180157）

黄兴丰（1974—），男，江苏南通人，副教授，博士，主要从事中小学数学教育研究．

[责任编校：周学智、陈汉君]