小学高年级学生数学学习非智力因素常模及其等级评价标准的建构与应用——以天津市为例

王光明，彭宇佳，李 健

小学高年级学生数学学习非智力因素常模及其等级评价标准的建构与应用——以天津市为例

王光明1，彭宇佳1，李 健2

（1．天津师范大学 教育学部，天津 300387 ；2．人民教育出版社 课程教材研究所，北京 100081）

数学非智力因素的测量与评价已积累了一定成果，但针对测评工具的区域性常模研究尚不多见．以天津市小学高年级学生为研究对象，确定研究问题：（1）数学学习非智力因素的区域性常模是怎样的？（2）与所建常模相对应的等级评价标准是怎样的？（3）被试班级和个体的数学学习非智力水平如何？通过问卷调查法，对天津市11个区进行大规模取样，使用SPSS软件进行样本数据分析，建立常模与等级评价标准；利用个案研究法进行应用案例分析．研究结论：（1）基于《小学生数学学习非智力因素调查问卷》，通过百分等级常模和标准分常模相结合的方式，建立天津市小学高年级学生数学学习非智力总体常模和5个主维度常模；（2）将被试在数学学习非智力及其5个主维度上的表现分别划分了5个等级，结合操作性定义及学生年龄特征建立了相应的等级评价标准，并明确了不同等级学生的特点；（3）基于常模与等级评价标准，发现被试班级的创新精神较为薄弱，被试个体的认知动机和情绪稳定性表现不足，并对其提出改善建议．

小学高年级；数学学习；非智力；常模

1 问题提出

非智力因素，简称非智力．IN结合理论指出，在外界客观条件大致相同的情况下，非智力和智力共同影响学习者的学习成就[1]．但通常而言，人的智力往往相差不大，动机、意志、性格等非智力因素却可能出现较大差异．由此可知，非智力因素对人的发展格外重要．2020年，中共中央国务院印发《深化新时代教育评价改革总体方案》，强调关注学生的意志、信念、合作精神等非智力因素．数学是基础教育阶段学生学习的重要学科，已有研究表明数学学习非智力因素对学生数学学习影响颇大，不仅有益于学生学习效率的提升[2-4]，对学生数学学习成绩的提高也有着积极的促进作用[5-8]．

近年来，心理学界深刻地认识到非智力因素在学校教育工作中的重要作用和意义，并就非智力因素问题开展了大量研究．国内外研究者们已经编制出不少数学学习非智力因素测评工具[9-13]，并产生了一定的影响．此外，一些采用相关测评工具进行的研究也不断出现[14-17]，但这些研究多侧重于直接使用问卷进行调查与评价，往往缺乏评价的依据和参照，无法将测量结果置于同一参照标准下分析，这将影响到调查结果的客观性．

为提升数学学习非智力测评工具的实用性，基于《小学生数学学习非智力因素调查问卷》[18]，建立了小学高年级学生数学学习非智力因素常模及其等级评价标准，并对这一成果进行案例分析．研究问题包括：（1）小学高年级学生数学学习非智力因素的区域性常模是怎样的？（2）与所构建常模相对应的等级评价标准是怎样的？（3）被试班级和个体的数学学习非智力水平如何？

2 研究方法

2.1 测评工具

选取《小学生数学学习非智力因素调查问卷》为调查工具，问卷共包含44个题项，适用于小学高年级（五、六年级）学生数学学习非智力因素的调查．该问卷将数学学习非智力因素划分为5个主维度（动机、情绪情感、态度、意志和性格）和对应的11个子维度，子维度的操作性定义见表1．问卷的编制过程严谨，针对性较强，具有较好的信度和效度，可作为小学高年级学生数学学习非智力因素测评的有效工具[18]．

2.2 样本选取

选取天津市11个区的1 525名五年级、六年级学生进行问卷调查，共回收问卷1 480份．首先通过观察，剔除答案呈现规律性、一致性或回答不完整的无效问卷40份；再通过测谎题，剔除回答不一致的无效问卷80份；最终确定有效问卷1 360份，有效率为91.89%．对数据进行描述性统计，所得样本服从正态分布，符合进一步研究的要求．

2.3 常模及等级评价标准的建立过程

为了刻画调查对象的数学学习非智力在所属群体中的位置，选择建立百分等级常模和标准分常模，前者方便使用者了解被试的数学学习非智力水平，后者使各维度之间的测评结果具有可比性．此外，还进行了数学学习非智力（及其5个主维度）水平等级划分．建立常模的具体过程见图1．

表1 数学学习非智力因素各子维度操作性定义

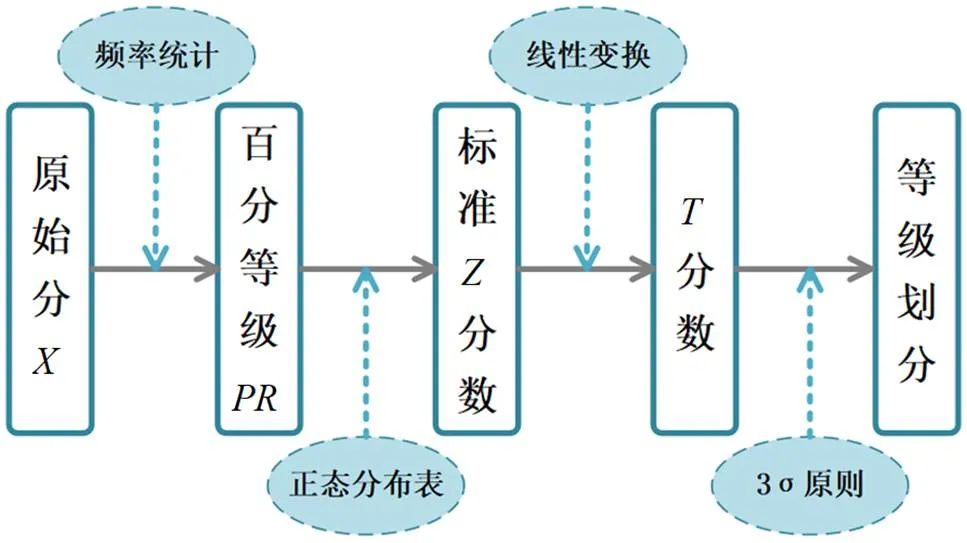
图1 常模建立过程

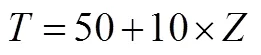
3 研究结果

3.1 数学学习非智力常模及等级评价标准

通过数据整理和分析，依据常模的构建方法建立小学高年级学生数学学习非智力因素常模（表略），及其对应的等级评价标准（表2）．为了更精细地诊断学生的数学学习非智力水平，接下来将分别从以下5个主维度展开研究．

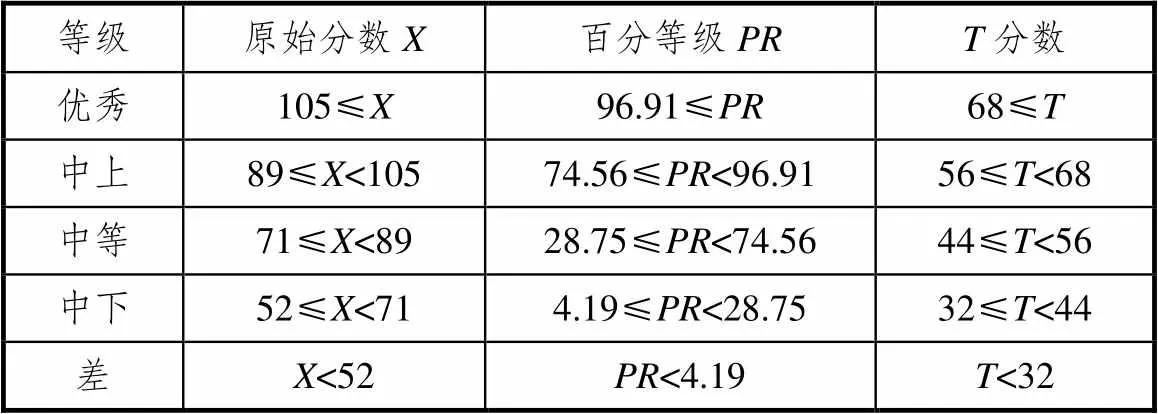
表2 数学学习非智力因素等级评价标准

3.2 动机维度常模及其等级评价标准

首先依据常模构建方法，建立动机维度常模（表略）．其次，对动机维度进行等级划分，进而制定对应的等级评价标准（见表3）．最后，分别计算不同等级学生在动机维度下的“成就动机”“交往动机”“认知动机”子维度上的平均分（见图2）．

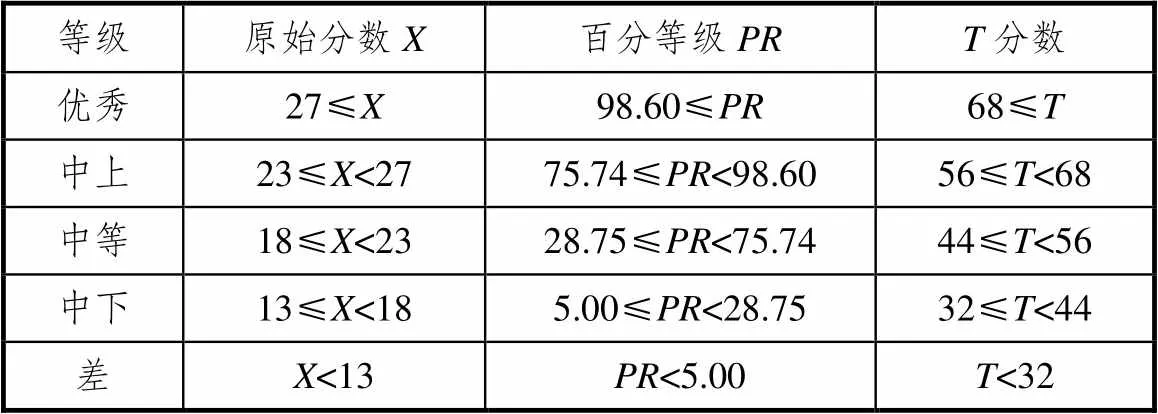
表3 动机维度等级评价标准

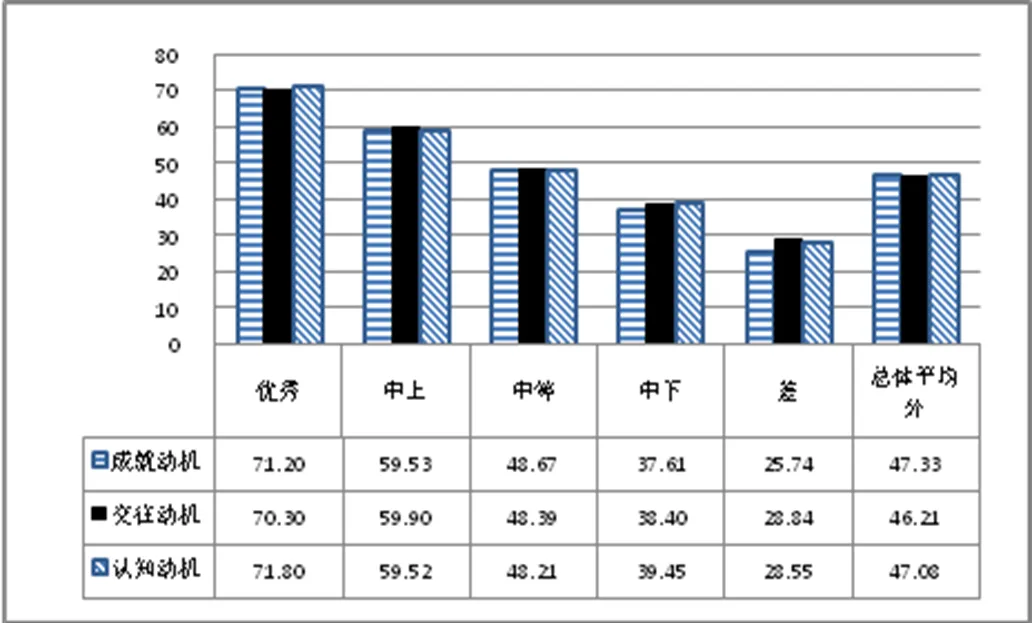
图2 动机维度的子维度T分数

在图2的基础上，结合数学学习动机各子维度的操作定义、所对应的具体题目及小学生年龄特征，确定不同等级学生的特点如下：优秀等级学生的数学学习兴趣浓厚且广泛，不仅喜欢数学，也喜欢数学史、数学文化等相关数学知识．这类学生喜欢钻研有挑战性的题目，求知欲强、好奇心大，渴望在数学上取得成就．中上等级学生对数学学习有兴趣和好奇心，愿意了解一些数学史、数学文化等与数学相关的课外知识．这类学生遇到难题也能够继续探究，不放弃，渴望有机会展现自己的才能．中等等级学生对待数学能够表现出动力、兴趣以及在该领域获得成功的欲望，愿意花时间直接提高数学成绩，但对于拓展性的课外数学知识不太感兴趣．这类学生在遇到数学难题时，会进行简单探究，但尝试未果后往往选择放弃，缺乏强烈的解决问题的动机．中下等级学生对数学学习的兴趣和各方面的动力均较弱，不认为课堂中的数学知识或数学史等课外知识是有趣的，不喜欢钻研难题，学习中更倾向于被动性地接受知识．差等级学生缺乏数学学习的兴趣和动力，甚至对有益于提高成绩的数学知识也不感兴趣．这类学生不会为了得到他人的肯定而努力，遇到数学学习困难时会直接选择放弃．

3.3 情绪情感维度常模及其等级评价标准

首先依据常模构建方法，建立情绪情感维度常模（表略）．其次，对情绪情感维度进行等级划分，进而制定对应的等级评价标准（见表4）．最后，分别计算不同等级学生在“情绪情感”维度下的“情绪稳定性”“情感体验性”子维度上的平均分（见图3）．

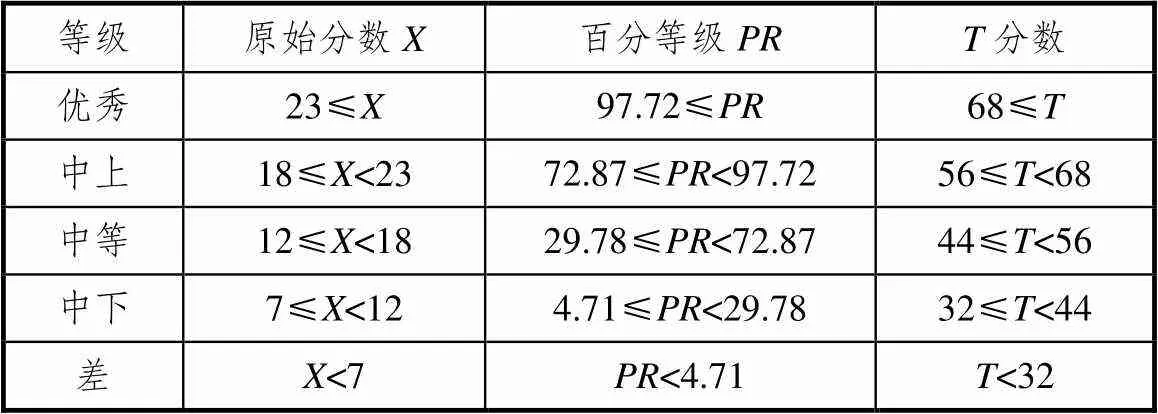
表4 情绪情感维度等级评价标准

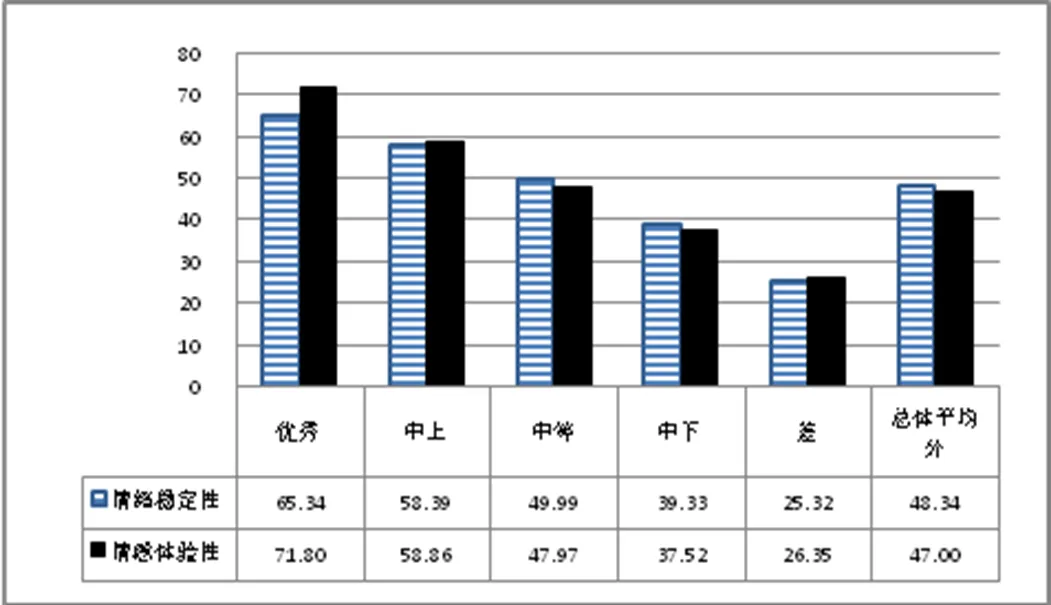
图3 情绪情感维度的子维度T分数

在图3的基础上，结合数学学习情绪情感各子维度的操作定义、所对应的具体题目及小学生年龄特征，确定不同等级学生的特点如下：优秀等级学生能够很好地调节和把控自己的情绪，不会随外界或内部的变化而产生波动，能够悦纳自己，将自己的优势转变为积极乐观的学习心态，自信心强，相信自己能够出色地完成数学学习．中上等级学生在出现不良情绪时能够及时进行调节和把控，可以及时克服并转化消极情绪，从而获得积极乐观的情感体验．这类学生相信自己能够胜任并完成数学学习．中等等级学生在数学学习中容易出现消极情绪，并且情绪会受外界环境的影响而变化，但这类学生相信自己能够胜任大部分数学学习．中下等级学生在学习中时常会出现消极情绪，并且自信心不足，心理素质较弱，认为自己的能力不足以胜任大部分数学学习．差等级学生对自我情绪的调节和管控能力均较弱，易产生排斥情绪和消极的情感体验，并且心理素质较差，自信心弱，认为自己无法胜任数学学习．

3.4 态度维度常模及其等级评价标准

首先依据常模构建方法，建立态度维度常模（表略）．其次，对态度维度进行等级划分，进而制定对应的等级评价标准（见表5）．最后，分别计算不同等级学生在态度维度下的“学科态度”“学习态度”子维度上的平均分（见图4）．

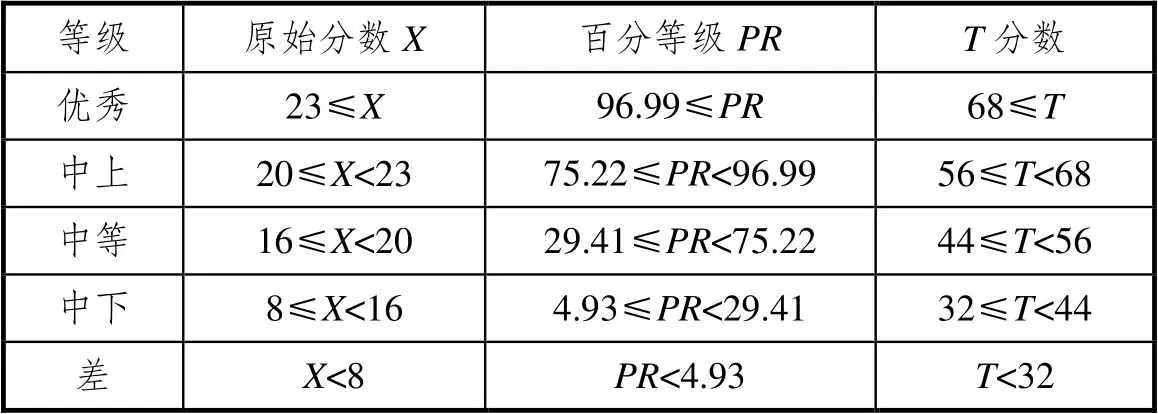
表5 态度维度等级评价标准

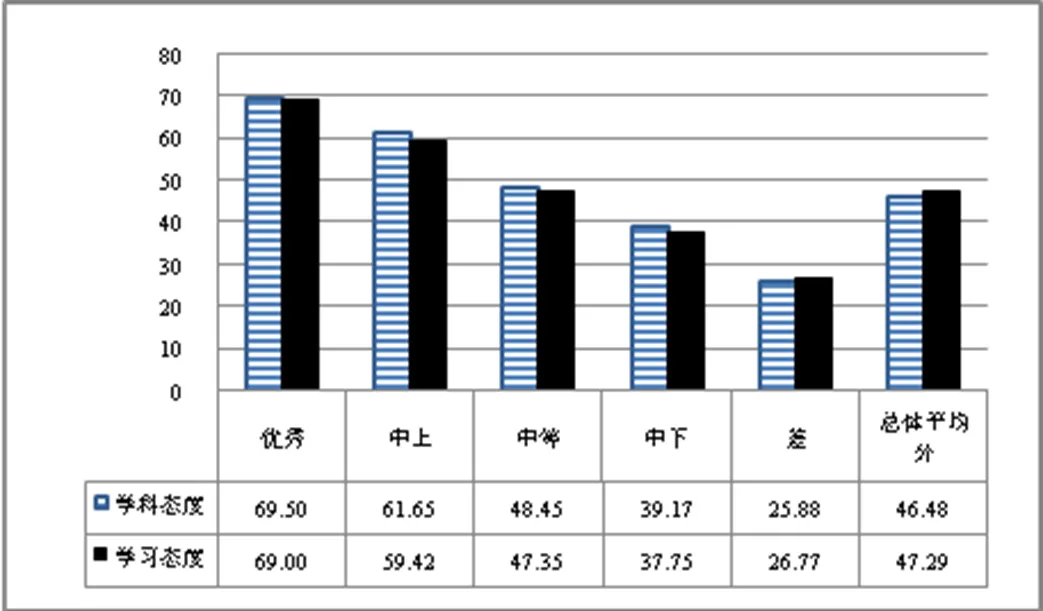
图4 态度维度的子维度T分数

在图4的基础上，结合数学学习态度各子维度的操作定义、所对应的具体题目及小学生年龄特征，确定不同等级学生的特点如下：优秀等级学生能够理解数学学科的价值和必要性，发现数学知识间的内在联系，解题的思想方法也是相通的．这类学生在学习中善于反思和总结，能够严格要求自己的学习行为和态度．中上等级学生能够客观认识数学学科的价值和必要性，能够理解数学知识间的内在联系．这类学生在学习中能够反思和总结，并能够控制自己的学习行为和态度．中等等级学生对数学学科的价值和必要性有所了解，在教师的指导下也能够认识到数学知识间的内在联系，以及解题思想方法间的相通性．但这类学生在学习中缺乏技巧性，不善于反思和总结适合自己的方法，对自己的学习行为和态度也要求不严格．他们更倾向于接受教师授予的解题方法，时常选择接受性学习．中下等级学生对数学学科的价值和必要性的理解较为片面，不认同数学知识间具有内在关联，也不认为数学解题方法之间具有相通性．这类学生在学习中不会积极主动地思考，尽管在教师监管下可以顺利完成数学学习任务，但经常会表现出懒散等学习态度．差等级学生不认同数学学科的价值和必要性，在学习的过程中毫无技巧性可言，解题时只在乎对错，不在乎字迹工整和过程、方法是否简便等问题，并且不善于总结出错原因，经常重复犯错，对于困难题目也会直接选择放弃．

3.5 意志维度常模及其等级评价标准

首先依据常模构建方法，建立意志维度常模（表略）．其次，对意志维度进行等级划分，进而制定对应的等级评价标准（见表6）．最后，分别计算不同等级学生在意志维度下的“坚持性”“自律性”子维度上的平均分（见图5）．

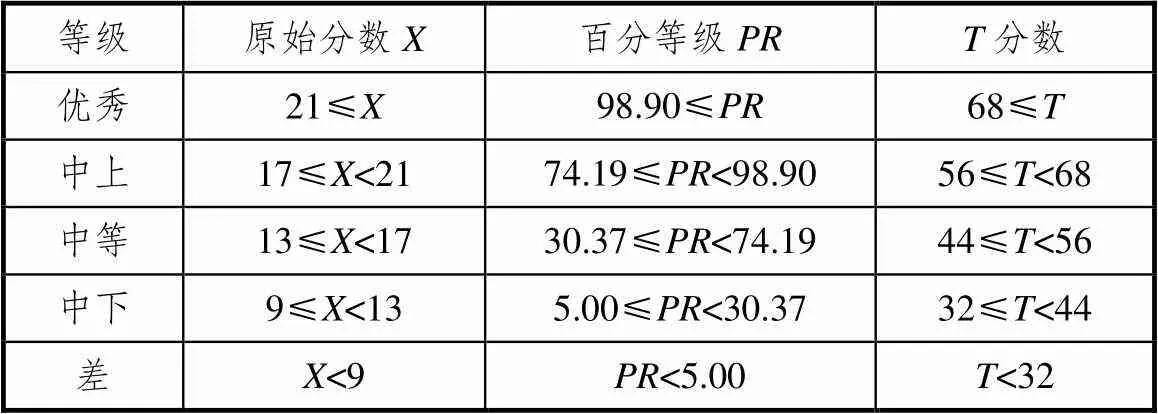
表6 意志维度等级评价标准

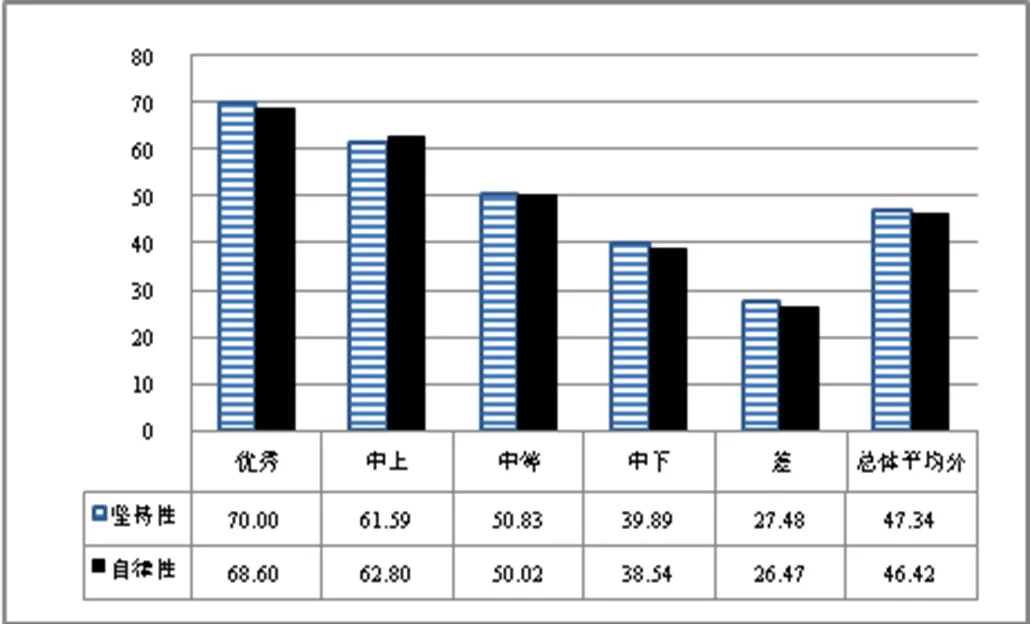
图5 意志维度的子维度T分数

在图5的基础上，结合数学学习意志各子维度的操作定义、所对应的具体题目及小学生年龄特征，确定不同等级学生的特点如下：优秀等级学生在遇到困难时能够迎难而上，不轻言放弃．这类学生在学习上严格要求自己的行为，能够按时完成学习计划或日常学习任务．他们课上不会走神或开小差，能够始终跟随教师的思维，具有较强的自我管理能力．中上等级学生具有一定的自我管理能力，多数时候遇到困难也能够尝试去挑战、去克服．这类学生能够主动完成学习计划或日常学习任务．他们在数学学习上认真踏实，不易受到外界环境的干扰，课上能够跟随教师的思维，不易开小差．中等等级学生能够主动执行学习计划或日常学习任务，但有时会因为缺乏毅力而无法完成，需要教师及时提醒．他们在课上偶尔会开小差，但在意识到走神之后可以迅速回归课堂．中下等级学生自我管理能力较弱，遇到数学学习困难时容易选择放弃．面对制订的学习计划或日常学习任务，这类学生经常需要在教师的督促下才能顺利完成．他们课上容易开小差，需要教师及时提醒．差等级学生自我管理能力差，遇到数学学习困难时首先会选择逃避和退缩．对于制订的学习计划或日常学习任务，他们常常会因为懒惰或其它外部因素而放弃，即使是在教师或他人的监管下也很难完成．他们课上能够集中注意力的时间较短，意志力较差，需要教师时常提醒．

3.6 性格维度常模及其等级评价标准

首先依据常模构建方法，建立性格维度常模（表略）．其次，对性格维度进行等级划分，进而制定对应的等级评价标准（见表7）．最后，分别计算不同等级学生在性格维度下的“质疑精神”“创新精神”子维度上的平均分（见图6）．

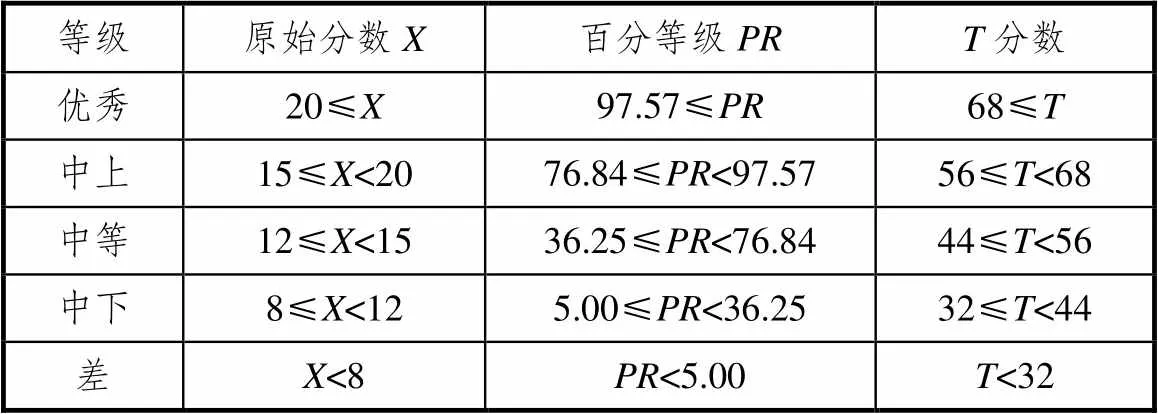
表7 性格维度等级评价标准

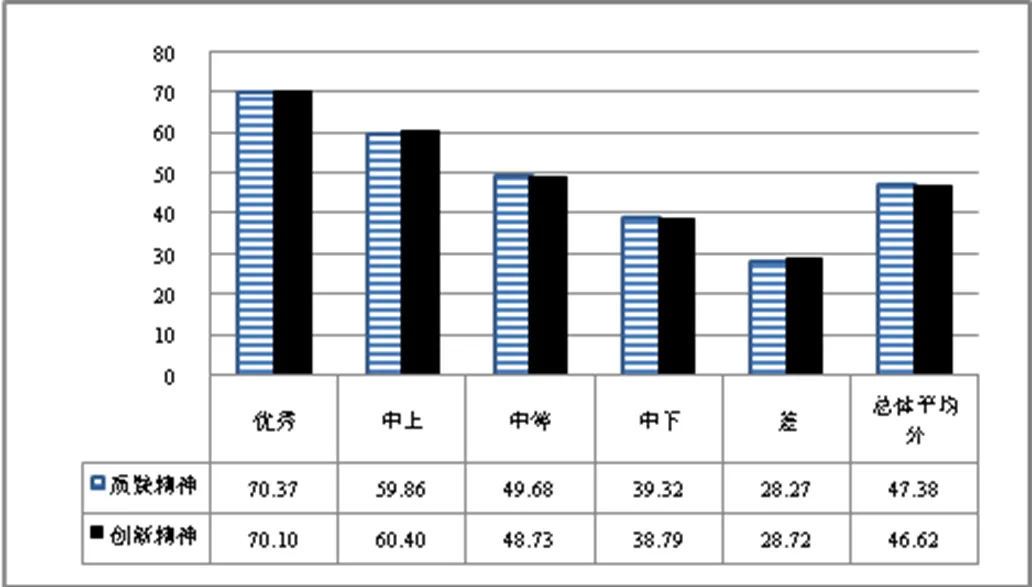
图6 性格维度的子维度T分数

在图6的基础上，结合数学学习性格各子维度的操作定义、所对应的具体题目及小学生年龄特征，确定不同等级学生的特点如下：优秀等级学生对数学知识有着自己独到的思考，不完全听信于权威，思维不局限于书本，能够坚持自己的想法，并主动与教师进行探讨．这类学生不仅能够将各类知识融会贯通，还能将新知识与自己原有的知识进行结合，应用在实际生活中．他们在解题上喜欢挑战难题，愿意尝试不同的解法．中上等级学生能够合理地思考数学知识，当自己的思考和书本（或教师所讲）不一致时，多数时候能够坚持自己的看法，并主动询问教师．他们能够发现各类知识之间的联系，并将部分所学数学知识应用于生活中．在问题解决中，如果教师给出的解法不够简便、巧妙，他们会主动尝试不同的解法．中等等级学生能够在教师的带领下主动思考，当自己的想法与书本或教师的呈现不一致时，多数情况下能够坚持自己的想法，但不会主动请教教师．这类学生在学习上能够理解各类知识之间的联系，但有时缺乏深入思考与探究．解题时，如果教师已经给出了简便的方法，他们就不会再额外尝试其它方法．中下等级学生不善于主动思考，会将教师给出的数学结论或方法直接应用到问题解决中，当产生与教师或书本中呈现内容不一致的认识时，会进行一定思考，但最终仍会服从于权威．在学习上，这类学生能够发现一些知识间的联系，但由于能力不足，无法进行理解操作．解题时，他们会直接运用教师给出的解法，不论此方法是否最简单．差等级学生不会主动思考数学知识，也没有将各类知识以及新旧知识联系起来的意识．对于已经被告知的答案，这类学生不会主动思考答案产生的原因及过程．他们的怀疑精神严重缺失，对教师、教材、教辅资料严重盲从，完全没有自己想法．

4 应用案例

对天津市Y小学五年级一个普通班的学生进行数学学习非智力因素调查，从班级测评和个体测评两个角度进行诊断分析，并针对结果给出改进建议．

4.1 班级应用案例

4.1.1 被试班级数学学习非智力的诊断分析

被试班级共有40名学生参与测试，有效问卷39份，问卷有效率为97.5%．被试班级学生的数学学习非智力原始平均分为85.13，所处的百分等级为66.03，说明该班在数学学习非智力的表现上，超过了天津市约66%的小学高年级学生．被试班级的数学学习非智力各维度分数为：51.15（动机）、52.46（情绪情感）、55.74（态度）、53.90（意志）、46.50（性格），以下将从5个主维度入手，对被试班级的测评表现做进一步诊断分析．

通过被试班级主维度分数雷达图（图7）可知：被试班级学生在5个主维度上的表现均达到天津市“中等”水平，在态度、意志、情绪情感、动机4个主维度上的得分逐个递减，但这4个主维度的得分均比较接近天津市“中上”水平的下限值．相对而言，性格维度与其余4个维度之间又有明显的差异，性格维度的得分十分接近天津市“中等”水平的下限值，因此，有必要对性格维度做进一步细化分析．

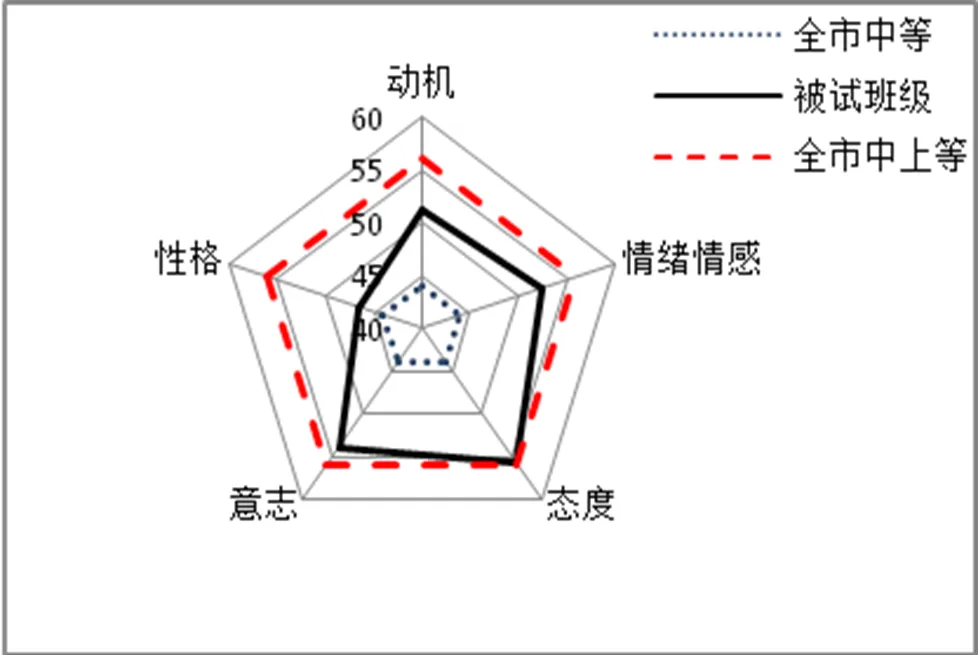
图7 被试班级数学学习非智力的主维度T分数

性格维度所属的两个子维度分数分别为49.8（质疑精神）和42.6（创新精神）．通过与天津市整体水平的比较（见图8），发现被试班级的质疑精神处于天津市中等水平，而其创新精神处于中下等水平．

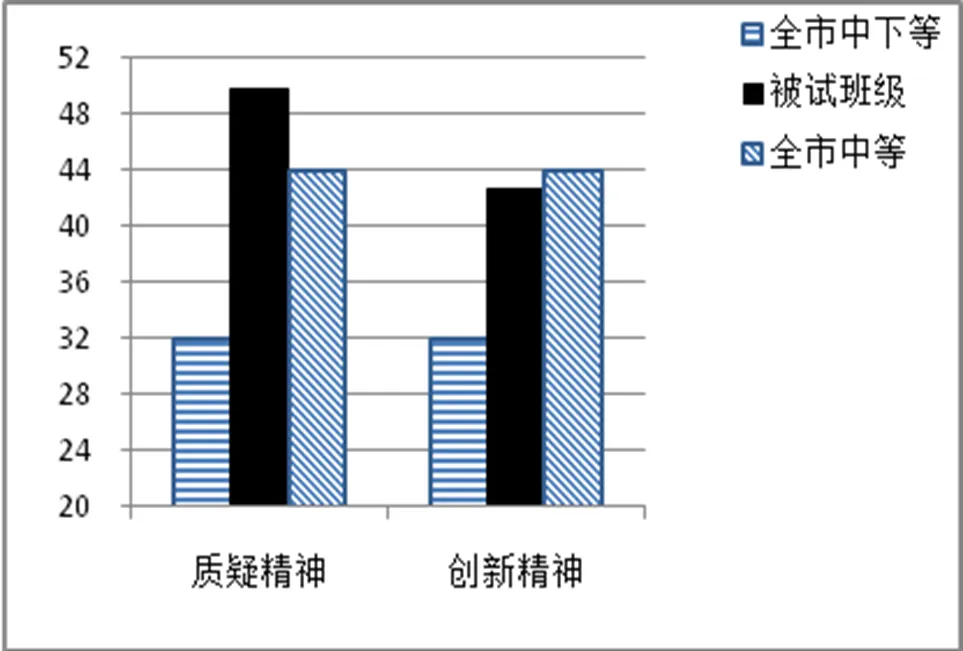
图8 被试班级性格维度的子维度T分数

通过以上逐步细化的诊断，得出诊断结果：被试班级的数学学习非智力整体表现一般，处于天津市中等水平，在5个维度上均有一定提升空间．其中，尤其应该加强的是性格维度下的创新精神子维度的培养．只有做到“全面发展+重点提升”，才能保证被试班级学生的数学学习非智力得到良好发展．

4.1.2 被试班级数学学习非智力水平改进建议

由于被试班级的数学学习非智力整体水平尚可，但在创新精神子维度上表现薄弱，故针对比较薄弱的创新精神子维度提出改善建议．对于创新精神的培养，深度的知识学习是基础，发散的思维方式是关键，有利的学习环境是保障．因此，首先教师应聚焦课堂，改善教学方式，让学生通过主动构建获得知识的深度理解[19]．其次，教师应注重对学生非逻辑思维能力的培养，包括联想、猜想、逆向思考、发散性思考等．有时学生的创新往往来源于他们不经意的一个联想[20]．最后，采取一些措施为学生创设有利创新的学习环境．日常教学中，为学生创设轻松的学习环境，营造宽松愉悦的课堂氛围，鼓励学生大胆讲出其想法（包括质疑、批判等），不要禁锢学生的思维．在日常练习中，调整对学生的评价方式，适当减少记忆性知识的考核，增加创新型、开放型、应用型问题的使用，并且不要严格限制学生的解题思路和方法，鼓励学生一题多解，注重多角度思考问题．

4.2 个体应用案例

4.2.1 被试个体数学学习非智力的诊断分析

根据被试班级数学教师的建议，在征得学生及其家长同意的前提下，从被试班级中选出一名成绩不够理想但学习态度较为端正的学生作为研究对象．该生数学学习非智力水平的整体原始分数为70，对照表2可知处于天津市“中下等”水平，仅超过天津市约26.18%的小学高年级学生．

具体而言，该生的数学学习非智力各子维度分数分别为：51.7（成就动机）、45.0（交往动机）、41.0（认知动机）、38.2（情绪稳定性）、45.2（情感体验性）、60.6（学科态度）、61.9（学习态度）、48.4（坚持性）、46.7（自律性）、47.3（质疑精神）、45.3（创新精神），由图9可知：该生的学习态度和学科态度表现较好，处于天津市“中上等”水平，但在认知动机和情绪稳定性维度上的表现明显不足，均处于天津市“中下等”水平，其余7个子维度表现一般，均处于天津市“中等”水平．

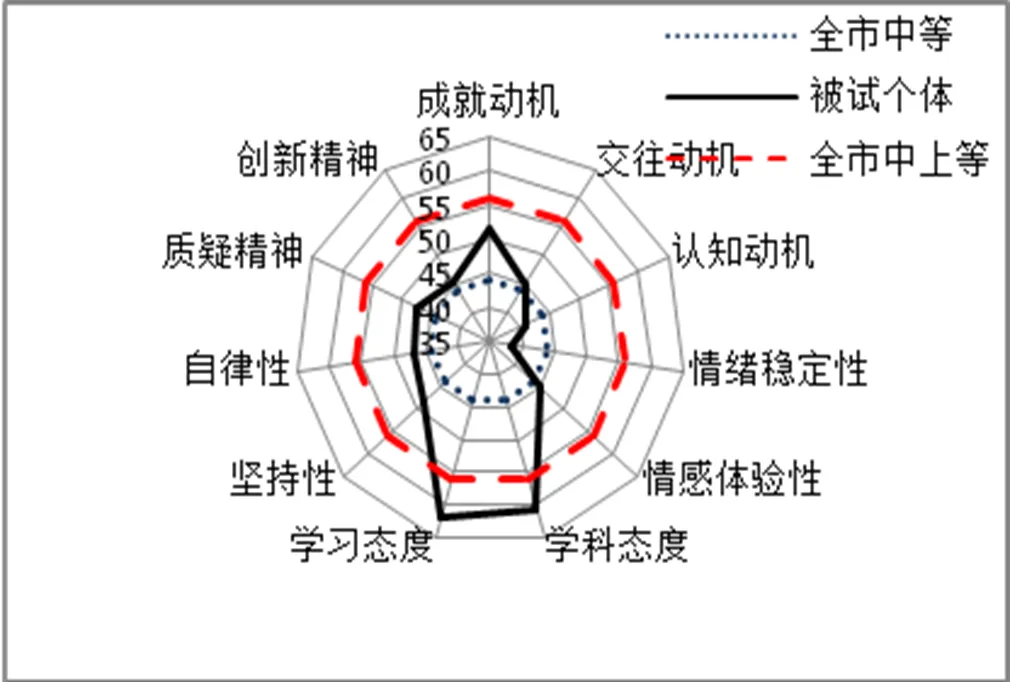
图9 被试个体数学学习非智力的子维度T分数

4.2.2 被试个体数学学习非智力水平改进建议

由于被试学生的认知动机和情绪稳定性较为不足，故针对这两个子维度对被试学生提出提升建议．关于认知动机的培养，由于兴趣对数学学习具有重要的导向和动力功能[12]，对钻研数学起着激励的作用[21]．所以教师可以通过激发学生兴趣的方式加以实现．具体地，在教学中加强学生对数学学习意义的认识，阐明数学在现实世界中的应用价值以及与相关数学知识间的内在联系．关于情绪稳定性的提升，由于该生本身数学基础薄弱，成绩不好，所以教师应联系家长告知该生实际情况，通过家校合作，对学生进行多角度的心理疏导，进而帮助学生掌握控制和调节自己情绪的方法，防止其发展为厌学情绪．

4.2.3 对被试个体的干预及效果

通过与被试个体数学教师的交流，发现该生在各维度上的特征描述与其在数学学习心理的外部表现大致相符．接着，与被试个体进行针对性交流，该生表示自己对与数学相关的奇闻逸事或无益于提高成绩的知识都不感兴趣，并且没有认知的意愿；该生还表示，自身在数学学习中时常会有过激情绪，但不会去刻意调节或控制．可见该生在认知动机、情绪稳定性方面的表现确有明显不足，这与常模和等级评价标准的刻画大致相当．

基于以上研究结果，联系其班主任对该生的认知动机和情绪稳定性进行干预，具体方法见上文中的建议部分．经过4个月的指导，分别在第二个月末和第四个月末进行数学测试，发现该生第二个月的数学成绩排名较上学期期末有所提升，第四个月的排名比第二个月的排名又有明显提升．经过一段时间干预后，班主任表示：该生对数学知识及相关的课外知识的兴趣明显增加，并且逐渐能够意识到数学知识对社会生活和自身的意义，从而将其转化为努力学习的动力；在学习的情绪情感方面，由于数学成绩有所提升，该生对考试及教师的恐惧有所减少，课上也能够冷静大胆地回答问题．

班主任认为该常模应用研究较为有效，通过常模表和等级评价标准，能够对班级总体及每一位学生的数学学习非智力水平进行清晰地认识，建议部分也具有可实施性．该生认为常模应用研究对自己的数学学习行为特征描述较为准确，通过天津市小学高年级学生数学学习非智力因素常模表和等级评价标准，能够了解自身的数学学习非智力水平，以便锚准不足，重点改善．在依据建议进行为期4个月的干预后，学习效率和效果得到了明显提升，自身的非智力水平也得到了提升．

5 讨论

相比于已有的天津市初中生、高中生的数学学习非智力水平常模研究[22-23]，这里主要体现出两方面的改进．

第一方面，加强了等级评价标准中对学生特点的表述．在初中生、高中生的常模研究中，对学生等级特点的描述时，年龄特征的体现不够强，主要依据各子维度所对应的具体题目进行描述．结合11个子维度的操作性定义、所对应的具体题目以及小学生的年龄特征，对其数学学习特点进行了具体行为和思维的细致描述．

第二方面，验证了常模表及等级评价标准的应用效果．尽管以往研究在建立常模表和等级评价标准之后，也进行了应用案例分析，但只停留在刻画分析被试的非智力水平优劣及特征这一层面．在进行个体应用案例分析后，又对被试进行长达4个月的指导干预，并关注其干预后的数学学习行为变化、数学成绩排名变化以及其非智力水平的变化，以此验证研究的应用效果．

尽管研究在以上两方面做了改善，但仍存在一些局限性．一是所建立的常模理论是针对天津市而言的，尽管其适用对象也包括与天津市教育水平相当的地区，但这类地区并不好确认．并且对于全国范围内的小学高年级学生的数学学习非智力水平，还需要后续研究者做进一步补充，全国性常模的建立将具有更大的应用意义．此外，研究所建立的常模具有一定的时效性，因为常模建立所选数据都是当下测验所得到的，所以随着时间的推移和教育水平的发展，常模需要不断地更新．

6 结论

首先，建立了天津市小学高年级学生的数学学习非智力总体常模与5个主维度常模．当学生的非智力总体原始分数大于等于105、89、71、52时，其非智力分别超过了天津市约96.91%、74.56%、28.75%、4.19%的学生．当学生的动机原始分数大于等于27、23、18、13时，其动机水平分别超过了天津市约98.60%、75.74%、28.75%、5%的学生；当学生的情绪情感原始分数大于等于23、18、12、7时，其情绪情感水平分别超过了天津市约97.72%、72.87%、29.78%、4.71%的学生；当学生的非智力态度原始分数大于等于23、20、16、8时，其态度水平就超过了天津市约96.99%、75.22%、29.41%、4.93%的学生；当学生的非智力意志原始分数大于等于21、17、13、9时，其意志水平分别超过了天津市约98.90%、74.19%、30.37%、5.00%的学生；当学生的非智力性格原始分数大于等于20、15、12、8时，其性格水平就超过了天津市约97.57%、76.84%、36.25%、5.00%的学生．

其次，将天津市小学高年级学生的数学学习非智力被划分为5个等级，各等级及其对应原始分数为：“优秀”（≥105），“中上”（89≤<105），“中等”（71≤<89），“中下”（52≤<71），“差”（<52）．动机维度的5个等级及其对应原始分数为：“优秀”（≥27），“中上”（23≤<27），“中等”（18≤<23），“中下”（13≤<18），“差”（<13）．情绪情感维度的5个等级及其对应原始分数为：“优秀”（≥23），“中上”（18≤<23），“中等”（12≤<18），“中下”（7≤<12），“差”（<7）．态度维度的5个等级及其对应原始分数为：“优秀”（≥23），“中上”（20≤<23），“中等”（16≤<20），“中下”（8≤<16），“差”（<8）．意志维度的5个等级及其对应原始分数为：“优秀”（≥21），“中上”（17≤<21），“中等”（13≤<17），“中下”（9≤<13），“差”（<9）．性格维度的5个等级及其对应原始分数为：“优秀”（≥20），“中上”（15≤<20），“中等”（12≤<15），“中下”（8≤<12），“差”（<8）．再结合操作性定义及小学生年龄特征建立5个主维度的等级评价标准，明确不同等级学生的特点，便于使用者诊断．

最后，基于常模与等级评价标准，发现被试班级的创新精神较为薄弱，建议教师改善教学方式，关注学生非逻辑思维培养，提供有利于创新的学习环境；发现被试个体的认知动机和情绪稳定性较为不足，建议教师加强学生对数学学习意义的认识，并通过家校合作帮助学生调控情绪．

[1] 燕国材．非智力因素与教育改革[J]．课程·教材·教法，2014，34（7）：3-9．

[2] 沈德立，白学军．高效率学习的心理机制研究[J]．心理科学，2006（1）：2-6．

[3] 王光明，刁颖．高效数学学习的心理特征研究[J]．数学教育学报，2009，18（5）：51-56．

[4] 康玥媛，张楠，王光明，等．高效率数学学习高中生数学成绩的影响路径[J]．心理与行为研究，2016，14（3）：352-359．

[5] POROPAT, ARTHUR E. A meta-analysis of the five-factor model of personality and academic performance [J]. Psychological Bulletin, 2009, 135 (2): 322-338.

[6] 颜中玉．非智力因素对高师数学学习影响的调查[J]．数学教育学报，2001，10（2）：44-47．

[7] 梁好翠，黄岳俊．数学自我监控及学习动机对数学成绩影响机理的研究[J]．数学教育学报，2011，20（1）：58-60．

[8] 彭乃霞，向毅，姚惠．非智力因素对数学概括能力的影响研究——基于来自贵州少数民族地区的样本[J]．数学通报，2015，54（5）：13-16，23．

[9] RYANG D. Development and validation of the mathematics teaching efficacy scale: Confirmatory factor analysis [J]. The Mathematical Education, 2014, 53 (2): 185-200.

[10] 李顺雨，田澜．高中生数学焦虑问卷的初步编制[J]．数学教育学报，2014，23（6）：63-67．

[11] 王宏，张守臣．小学生数学学业情绪问卷的修订[J]．数学教育学报，2018，27（3）：62-65．

[12] 裴昌根，宋乃庆，刘乔卉，等．数学学习兴趣测评指标体系的构建与验证[J]．数学教育学报，2018，27（2）：70-73．

[13] 王光明，李爽．初中生数学学习非智力因素调查问卷的编制[J]．数学教育学报，2020，29（1）：29-39．

[14] 熊建华．中学生数学焦虑及相关因素的调查研究[J]．数学教育学报，2008，17（3）：52-54．

[15] 隋佳源，徐亚．初三学生数学态度现状调查研究[J]．成都师范学院学报，2015，31（3）：117-120．

[16] 曹瑞，于川，于永东．高中生数学学习态度量表的修订及初步运用[J]．数学教育学报，2015，24（6）：57-60．

[17] 原露，元英，杜宵丰，等．主观规范对数学学习行为的影响：数学兴趣的中介作用[J]．数学教育学报，2020，29（5）：14-19．

[18] 冯玉琴，王光明，李健．小学生数学学习非智力因素调查问卷的设计与编制[J]．考试研究，2021，17（1）：79-87．

[19] 王萍萍，鲍建生，周超．中小学生数学创造力培养的研究述评——聚焦课堂[J]．数学教育学报，2018，27（6）：22-28．

[20] 邓清，夏小刚．数学思维视域下“教表达”的再认识与思考[J]．数学教育学报，2019，28（5）：47-50．

[21] 沈威．徐利治数学教育思想研究[J]．数学教育学报，2019，28（1）：74-78．

[22] 王光明，李健，简婧娴．初中生数学学习非智力水平常模及其等级评价标准研究——以天津市为例[J]．教育理论与实践，2020，40（20）：44-48．

[23] 王光明，刘晓昱，李健．高中生数学学习非智力特征的常模及其水平等级标准研究——以天津市为例[J]．天津师范大学学报（基础教育版），2017，18（3）：50-59．

Determination and Application of Norms and Grading Criteria of Upper Primary School Students’ Noncognitive Factors in Mathematics Learning——A Case of Tianjin

WANG Guang-ming1, PENG Yu-jia1, LI Jian2

(1. Faculty of Education, Tianjin Normal University, Tianjin 300387, China;2. People’s Education Press Curriculum and Teaching Materials Research Institute, Beijing 100081, China)

There are studies for measuring noncognitive factors in mathematics, but little research has been conducted to establish regional norms of noncognitive factors in mathematics. Taking upper primary school students in Tianjin as the sample, this study is designed to answer the following research questions: (1) What is the regional norm of noncognitive factors in mathematics? (2) What is the grading criteria with respect to the established norm? What are the characteristics of students at different grading levels? (3) What are the grading levels using classes and individuals as the units of analyses? This paper reports results from the questionnaire survey of a large-scale sample of 11 districts in Tianjin. Through the use of SPSS software to analyze the sample data, we have established norms and grading criteria, and also conducted a case analysis. We have reached the following conclusions: (1) based on the, the overall norm and main dimension norms for noncognitive in mathematics learning of upper primary school students in Tianjin were established by combining percentile norms and standard norms; (2) the subjects’ overall responses in noncognitive factors in mathematics learning and responses in each of the five subdomains were divided into 5 levels, combined with operational definitions and the age characteristics of students to establish the corresponding grading criteria, with clarified characteristics of students in different grades; and (3) based on the norms and grading criteria, it was found that the innovation spirit of the class was relatively weak, and the cognitive motivation and emotional stability of the individuals was relatively insufficient. Feasible suggestions for the weak links of the diagnosed object are proposed.

upper primary school; mathematics learning; noncognitive factors; norm

G622

A

1004-9894（2021）03-0052-07

王光明，彭宇佳，李健．小学高年级学生数学学习非智力因素常模及其等级评价标准的建构与应用——以天津市为例[J]．数学教育学报，2021，30（3）：52-58．

2021-05-20

天津市教育科学“十三五”规划课题——天津市义务教育阶段学生数学学习质量评价研究（BE3282）

王光明（1969—），男，天津人，教授，博士，博士生导师，主要从事数学教育测评、数学课程与教学论研究．

[责任编校：周学智、陈隽]