数学教师合作学习的理论与实践之比较分析

丁莉萍

数学教师合作学习的理论与实践之比较分析

丁莉萍

（挪威科技大学 教师教育系，挪威 特隆赫姆）

运用Boylan等选取的关于教师信念与实践之间关系的学习模式分析框架，选取中国内地、中国香港，以及美国的3个典型教师合作式学习模式，从学习模式的主要要素及其关系、相关的学习理论，以及研究方法与实践操作等方面做深入的比较分析．主要结论如下：第一，3个合作式学习模式的理论支撑都是参考一般化的学习理论（并非针对数学学科教学），研究的聚焦点都是考察教师学科专业知识的习得与课堂教学行为改进间的关系．第二，都混合了不同的研究方法以调动多种不同研究思维方式、方法的互动与融合．这一比较分析对于丰富中国本土数学教师合作学习的理论研究与实践具有3个方面的意义：（1）重视对中西方不同研究思维方式、方法的理解与运用；（2）反思教师合作学习模式应聚焦“谁的知识”的问题；（3）数学教师合作式教学研修及其研究是否需要强调其学科独有的默会知识？如何重视对其在本土文化社会情境的哲学范式层面的理论探索．这对中国建设有鲜明本土特色的数学教师教育研究的哲思体系与理论有着重大的意义．

教师的合作学习模式；研究方法与设计原理；学习理论；教师的信念与实践；教师的知识与实践

1 问题提出

在世界各地存在着多种多样的关于教师合作学习（teachers collaboration）的研究方法、理论与实践模式．例如中国和日本的教师课例学习（lesson study）、英国的行动研究（action research）和欧美的设计研究（design research）等[1-6]．ICMI Study 25旨在解决关于数学教师合作、共同学习与成长之间复杂关系等相关理论问题与实践挑战．根据ICMI Study 25会议A专题组丁莉萍与Jones的报告[7]，针对数学教师合作学习理论和实践做进一步深入分析与探讨．在ICMI Study 25A组专题报告中，研究者侧重于讨论以下两方面问题[7]：（1）现有的相关研究文献采用了什么理论观点和方法论？需要进一步研究调查的是什么？（2）研究教师的合作学习，什么是可操作的研究设计原理及其数据收集与分析方法？在此基础上，运用Boylan等选取的关于教师信念与实践之间关系的学习模式分析框架，通过比较分析，深入理解中西方研究者在不同国情及文化背景下对数学“教师合作学习”理论诠释以及采用的研究方法和实践方式．

选取以下3个在国际数学教师教育研究领域具有一定地域性影响力的教师合作学习模式：（1）中国华东地区的“教师行动教育课例研究”（简称行动教育模式）[8–9]；（2）中国香港地区的“教师学习变异理论与课堂实践”（简称变异理论学习模式）[10]；（3）美国的“教师学习团体为中心”（简称团体学习模式）[11]．之所以选取这3个教师学习为“合作学习”模式，是因为这3个模式都针对性地强调教师有效学习以及积极变化的发生和教师群体参与，并与专家学者互动交流密切相关．

2 教师学习模式的分析框架

Boylan等[12]提出的分析框架侧重于分析5个教师学习不同模式，特别针对教师信念（belief）与实践（practice）的关系，及考察影响教师学习的因素的不同研究途径与广度．Boylan等研究者[12]选取的5个教师学习模式中，Guskey[13]、Desimone[14]、Clarke与Hollingsworth[15]聚焦于教师信念与实践的关系不同学习路径与过程模式．第四个是Opfer与Pedder[16]提出的使用一个系统的学习概念的模式．第五个是Evans[17]的认知学习模式．Boylan等研究者[12]的分析框架包括：模式的主要素、目的、项目规模大小、关于学习理论的显性与隐性的支撑、教师主客体定位，及其参与学习的变化过程等（参见表1）．模式的主要素是指描述学习过程的主成分（教师信念与实践）及其之间关系．例如Guskey[13]的主成分为（1）教师职业发展，（2）课堂教学实践的变化，（3）学生学习结果的变化，（4）教师的信念与态度的变化；这4个成分之间关系为实践在先，信念改变在后的单向因果关系，即教师实践促进信念改变．关于教师学习，不同的研究者会用不同的术语（例如framework/model/form）描述研究框架和理论等．运用Boylan等[12]关于研究教师学习模式的分析框架和术语，统一使用教师学习模式（model）这一名词（以下简称模式）．选择Boylan等的分析框架做为文献分析框架，基于以下两个层面思考：（1）Boylan等在比较这5个教师学习模式异同点以及优缺点后，提炼出的分析框架和做文献研究的规范与方法值得国内研究工作者学习；（2）根据表1，可以针对文中分析的3个模式中“教师合作学习”的名词界定，教师学习及其研究所需的一般化学习理论与数学教师学习所需学科专业理论的关系，中西方不同的学习理论观点，思维方式与方法论等做进一步思辩．特别值得注意的是，表1未包括Boylan等的原分析框架的主要范畴之一是学术哲学范式（philosophical paradigms）[12]．因为同Boylan等的发现类似，选择分析的3个模式都尚未对此方面做详细阐释．其次，Boylan等“location of agency（actors that prompt or lead to change）”在表1中意译为“学习过程的主客体定位”．关于术语界定与翻译的问题，将在文章最后部分进一步讨论．

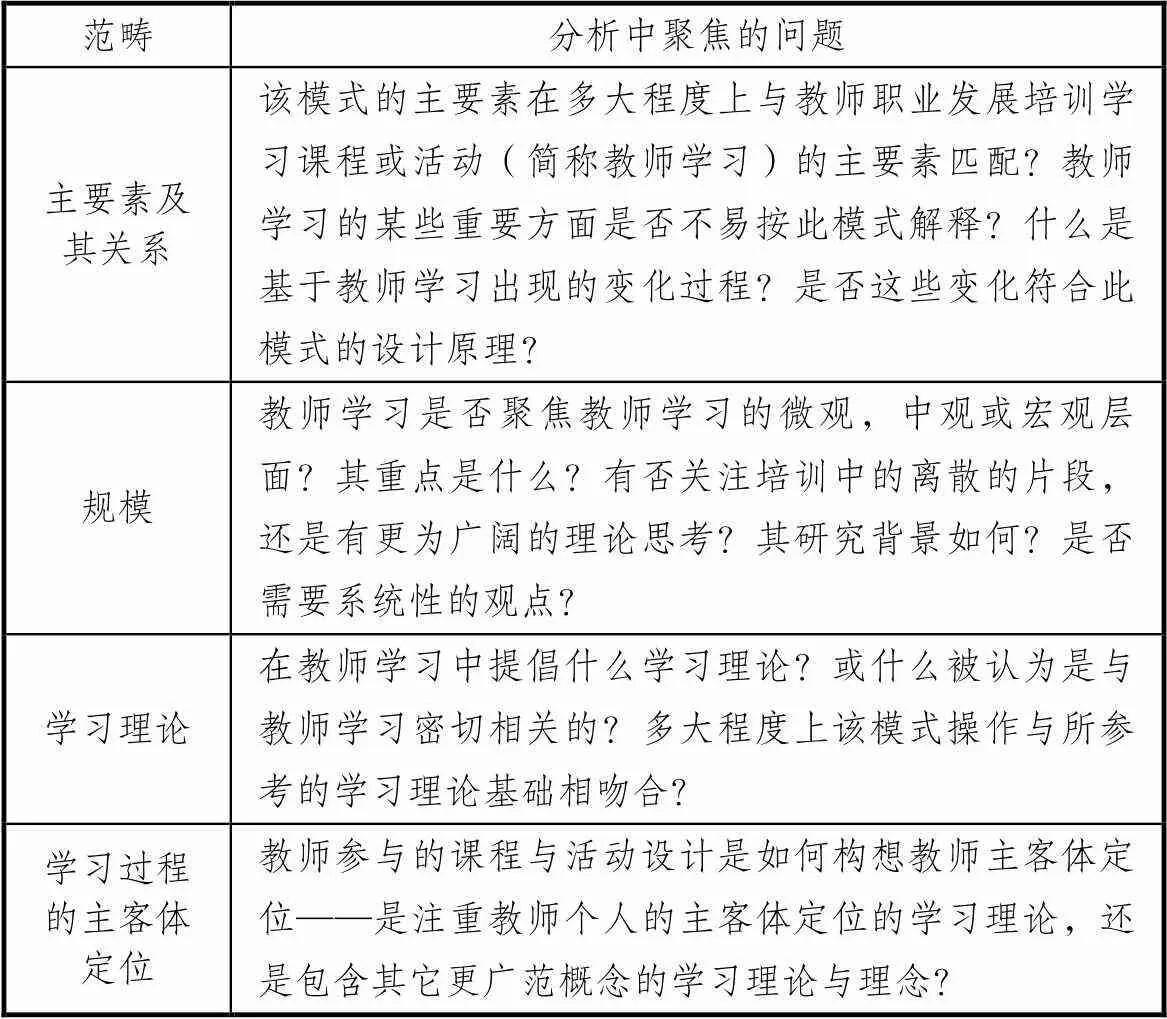
表1 教师学习模式的分析框架[12]

3 数学（学科）教师合作学习的3个模式

顾泠沅和王洁团队[9]提出的教师行动教育模式，是指在平时的教师培训形式之外提出一种以课例为载体，在教学行动中开展包括专业理论学习在内的教师教育．该模式的关注点是在课程改革中教师的专业成长需要，即有课例的专业引领和有行为跟进的全过程反思．顾非石与顾泠沅[8]进一步考察教师如何通过行动教育模式，特别是通过参与教师发展指导者（即国内各级教研员）的课例评课活动的指导学习，来促进数学课堂的教学效率与质量[8]．

Lo和Marton的变异理论学习模式重点关注以Marton的变异理论作为教师课堂教学设计原理的理论学习及课堂教学应用[10]．该模式于1999年在香港地区学校初次实践操作．进而，在世界其它国家和地区也被实质性地推广学习与实践，例如瑞典、文莱、英国等地．Lo和Marton指出，变异理论学习模式的初衷是使由教师和大学研究者组成的研究小组合作学习，发扬以变异理论为依据的教学设计原理与实践的潜在价值[10]．他们考虑该理论模式适用于研究者与一线教师共同探索如下问题：即研究者以变异理论为设计原理设定课堂教学目标．此目标又是如何通过研究者与教师的合作得以在课堂上有效实施的呢？

Borko的研究团队[11]研发了团体学习模式．该模式旨在为大学的关于教师专业发展的短期课程培训提供设计理论与操作模式指南．其主要关注点是培养在职中学教师学习、理解数学学科知识，并应用该知识提高数学课堂教学质量．该模式中教师的教学理论是以建构学习理论与情境学习理论为支撑的．Cobb等[18]在“关于教学设计研究法对提高在职教师专业学习与实践应用”一文中，将该模式作为北美地区大学教师教育课程的设计原理，用以匹配教师专业学习所需实践活动经验以及结合其职业工作环境及学习情境的一个成功案例．

4 数学（学科）教师合作学习3个模式的比较分析

运用Boylan等[12]关于研究教师学习模式的分析框架（见表1），对上述3种模式的主要素及其之间关系、规模、学习理论、学习过程的主客体定位进行分析与比较．在比较分析基础上，针对Boylan等研究者们选取的教师一般学习模式（信念与实践的关系）与ICMI Study 25所强调的数学教师如何通过运用合作学习模式，进而发展学科专业知识与实践的理论和研究方法做进一步深入分析与探讨．

模式1：行动教育模式

主要素及其之间关系．顾泠沅和王洁的团队[9]提出的行动教育模式体现了国内研究者西学中用的思想，即探索欧洲的行动研究、设计研究等科研方法与中国本土的学校教师教研学习，互相讨论和交流的传统，与中式课例研究模式[19]相结合的行之有效的混合型教师学习模式．该模式[9]的3个基本要素及其之间关系如下：（1）课例，它是行动的载体；（2）合作平台，研究者与教师的合作平台主要有理念学习、情境设计和行为反省；（3）运作过程，整个流程包括原行为（关注个人已有经验的教学行为）、新设计（关注新理念的课例设计）、新行为（关注学生获得的行为调整）3个阶段，期间有两轮在寻找差距中的反思与调整．简称“三行动两反思”课例活动．这样的流程多次往复，促进教师的教学理念与行为螺旋式地相互碰撞、交融，进而彼此更新．该课题团队[9]主要人员为教师和国内各省市区级教研人员、专家、大学研究者等．

顾非石与顾泠沅[8]在行动教育模式[9]基础上进一步提出调研教师发展指导者（即国内各级教研员）的两维指导工作框架：一是指导内容（即各类教师专业知识如数学学科知识、教学知识和实践性知识，即教师默会知识，该研究称之“行动知能”）；另一个是指导方式．该研究团队明确提出关于构想教师行动知能的4个核心要素，即目标分析、任务设计、过程测评、行为改进，并建立起四角关系模型以解释教师专业化学习的根本途径[20]．通过对指导者指导方式做归纳分析，研究者们得出以下4类指导策略：一般讲评、估计问题讲评、针对性指导、平等讨论．这里的先后次序表明了从指导者权威取向到指导者与教师平等互动取向的渐进层面．顾非石与顾泠沅[8]的研究发现之一是中国的教研员在课例评课交流活动中主要关注教师“行动知能”（默会知识）的指导．有趣的是，该研究揭示了促进教师数学教学行动知能所需3类主要专业知识的复杂的交融关系：即中国的教研员在课例指导活动中并非倾向于理论和知识的一般化和抽象化层面的讨论．他们的指导旨在帮助教师通过分析具体的教学案例来理解所涵盖的相关数学学科知识和其教学知识，即行动知能的知识构成部分．关于行动知能的四角关系模型，该研究揭示了中国教研员更关注教师们在教学任务设计与实施过程中教学行为的跟进，而较少关注教学目标的分析与教学过程测评．

规模．该研究项目[8]既聚焦教师学习的微观（即教师个体每时每刻的学习体验）和中观层面（即教师在校本教师研修的相关活动），也有的放矢在其宏观层面（即研究者的研究目的在于推广研究成果，使其服务于国家各级教师培训与研修的创新与行之有效的模式推广应用）．该研究[8]的初期阶段选择在浙江某小学的教师实施行动教育模式的实地教研指导活动．初期研究选择两位教师开展关于两位数退位减法的三轮两反思的模式操作．4位教研员被研究团队邀请参与全程指导教师完成课例研究．课前和课后对学生的学情进行了文本测试数据收集．所有的试教和课后评课活动都收集了录像数据．每节试教课后都对执教教师和部分学生进行录音采访数据收集．在该研究的后期，研究团队组织二十多位教研员（包括参与该研究项目指导教师的教研员）观摩该研究课题教师指导活动的录像，并尝试对此指导活动做学术层面的分析．例如指导活动的目的、实施行为、及取得效果的分析与解释．这一教研员集体观摩交流指导教师的活动也被录像作为该研究的后期数据收集．顾非石与顾泠沅[8]指出该研究的行动知能的模型是对行动教育模式[9]的进一步提炼，以便行动教育模式成为一种结合并发扬国内优秀传统的校本教师教研活动研修的共同学习理论及操作指导模式[1，3-4]．

学习理论．顾非石与顾泠沅[8]进一步突出了行动知能模型中两个有中国特色的学习理念：一个是行动智慧，即该研究的行动知能是指针对教师教学行为改进为目的的学科专业知识与教学知识的统一体；另一个是王阳明的知行合一理念．关于“学习理念”与“学习理论”的名词界定与区别，在文章最后的ICMI Study 25对中国数学教师合作学习的理论与实践意义部分进一步展开讨论．行动教育模式[9]与行动知能模型[8]的研究者们考察了大量关于实践性知识的特征的相关文献，例如西方文献中提出的实践中产生的知识与关于实践中已具备的知识等（详见文[8]）．研究者们提出国内教研员的实践性知识虽然与舒尔曼（Shulman）的PCK（pedagogical content knowledge教学内容知识）相似，却是建立在学科内容与教学内容知识融合之上的一种独特的教师默会专业知识．值得注意的是，行动教育模式[9]与行动知能模型[8]目前尚未对其主要素之间关系做理论上的充分诠释．即“三行动两反思”的学习过程中，到底是教师的教学理念更新在先，教学行为跟进在后，还是反之，目前尚待进一步理论建设和研究．

学习过程的主客体定位．该研究聚焦于国内优秀的数学教师教育工作者（如教研员）特有的针对帮助教师提高课堂教学效率的实践性知识的研修．该研究揭示了教研员侧重根据自身长期经验，对教师的教学问题进行前瞻性的综合性指导，是课例活动的主导者．然而，受课题时间限制，他们在该研究中无法确保有充分的时间，使教师对课例活动过程中产生的问题进行提问及深入的对话交流．这一发现与关于教师运用行动教育模式进行课堂教学设计的其它研究发现相左[21-22]．这恰恰说明在国内教师课例研究的共同学习里，教研员采用多种多样的合作方式指导教师共同学习．这一话题将在后面进一步展开讨论．

模式2：变异理论学习模式

主要素及其之间关系．Lo和Marton[10]的变异理论学习模式是一种日本教师课例研究模式[23]与Brown[24]、Collins[25]设计实验研究模式（design experiments）的混和模式．日本教师课例研究模式[23]的核心要素是课例．教师课例学习由8个步骤构成[26]：（1）界定问题；（2）准备教案；（3）试教；（4）评课和课后教学效果反思；（5）修改教案；（6）再试教；（7）再评课和课后反思；（8）分享课例教学成果．这与中国教师（及研究工作者）共同参与课例研究的备课—听课—评课—改进课的循环式研修模式类似．但是，值得注意的是，研究者[10]也根据Brown与Collins的设计实验研究方法，在强调“课例”这一要素之外，也突出了“设计”与“实验”两个新的要素．即研究者提倡在研究课例的活动中以Marton的变异理论为教学设计原理，整个课例研究组探讨该学习理论原理如何指导教师教学实验的实践操作．即该模式[10]同时强调教师教学实践层面的学习（课例），与理论层面的学习（通过反复、仔细地备课和评课过程，重视课例“为什么”与“如何”达到教学效果的问题）．

文[10]用两个课例片段展示变异理论作为教师教学设计的指导原理及实际操作．第一个案例是考查此模型如下主要素之间的关系：该教学片段介于第一轮和第二轮课例之间．数据还包括课前与课后学生学情测试．该模式的主要素之一就是教师对变异理论的学习和根据该理论的教学设计原理增进了理论层面的深入理解．例如，教师的学习体会仅仅利用变异理论的变异方式进行备课设计是不够的．课例的实施必须使学生亲历教学设计中的学习变异方式．因而，教师需要运用相应的教学策略使学生能经历备课设计中有针对性的变异学习方式．第二个案例的教学课题是中学电化课．课例片段主要展示研究课的备课与试教之间的关系，以及部分学生关于课堂学习结果的访谈．在此片段里，研究者指出一个变异理论不易解释的教师教学的重要方面．当课堂教学的目的变得复杂且要求学生同时关注一个以上的学习目标的关键特征时，变异理论并非总是很明确地指导变异方式的操作，以使学生获得理想的学习效果．在教学实践中，该研究[10]强调对教师的独创性能力的重视．在关于教学的科学性与艺术性这两个方面的思考与辩论中，研究者提出关于“教学艺术之科学”（the science of the art of teaching）的新观点．

规模．该研究混合了教师学习的微观、中观和宏观层面．通过香港教育学院的各类研究项目的实验，已操作完成了超过300个变异理论学习课题，许多当地学校建立了校本变异理论学习模式的课题组[10]．该模式被视为促进学生学习，缩小学生学习差距，并利于教师专业学习发展与研究者的学习的良好研究工具．

学习理论．Lo和Marton[10]建议可采用变异理论作为指导课堂教学的设计原理，并且把它作为一个重要的研究方法，用来促进基于教师学习的可持续性教学探究，关注学生学习的专业互动理论的发展．变异理论引领教师的课例研修，聚焦学生学习目标的分析，并针对教师了解关于学生学习的必要性条件提供了理论基础．但是，Lo和Marton[10]的变异理论对日本课例模式中强调的教师信念（belief）与教学实践（practice）之间的关系尚未做出阐释．

学习过程的主客体定位．该模式[10]里研究者和教师通过合作，尚待进一步去理解日本课例研究与西方设计实验研究的主要要素与教师教学实践所需专业知识学习之间的复杂联系．例如，课例模式中的教师群体合作学习路径，设计实验中关于变异理论在课堂教学设计中的隐性特征，与教师实施课堂教学策略的实践性知识．这些尚未明了的教学实践与默会知识之间的联系或许是日本课例模式在异地成功推广应用的基础性知识[10]．

模式3：团体学习模式

主要素及其之间关系．Borko的研究团队[11]设计了为期两周的大学暑期教师培训课程．其主要内容包括教师通过60小时的会议现场交流，以4个活动类型为主要素：数学问题解决、考查学生思维、阅读讨论当代文献，及自我反思学习心得．该研究团队分享了他们的努力，即研发大学教师教育学习课程的团体学习模式以提高教师的代数知识．

研究者们注重教师课堂教学生涯的4个特征，并认为这些特征是建立并保持成功的学习团体的基础：有安全感的工作环境；丰富的教学任务；学生的解释与思辨；分享思想的过程．该研究报道的第一个数据片段是从第一天暑期课程教师学习活动的摘录开始．该片段描述了教师培训者如何建立一个有安全感的教学环境并鼓励教师分享思想的学习文化氛围．第二个片段是发生在第四天的培训活动．其描述了教师培训者有针对性地指导教师拓展代数知识和代数思维．研究者在分析以上数据之后提出一系列该模式的操作与推广应用所遇挑战．例如，如何将此短期大学培训课程的模式进行推广应用？教师培训者的能力与性格之间关系如何？哪些是教师学习必备之长期支撑，用以帮助他们保持建立在此培训基础上的可持续专业成长？

规模．该研究介于教师学习的中观层面（大学暑期培训活动）．参与该研究暑期培训的16位教师来自3个不同学区．其中13位在初中任教，3位在小学任教．该暑期培训由两位该大学的数学教师教育者合作承担．他们是大学讲师及该研究项目的成员．

学习理论．该模式联系着两个关于教师专业发展的学习理论框架．一个是教师学习团体，即认识社会文化因素对教师专业学习的影响．另一个是教师教学所需知识（数学学科知识与数学教学知识），侧重教师教学知识的变化．研究者们考虑这个模式的一个独到之处是强化教师团体和数学理解这两个基本培训目标的共生关系．该暑期培训课程及其研究以情境式学习理论为基础考查教师的学习．例如，该研究重视教师进修学习时专业知识结构拓展过程中的情境的影响因素．但是，这两个学习理论框架尚未诠释教师研修课程中所获知识与课堂教学实践之间的直接关系，也未对教师信念与实践之间关系做出诠释．

学习过程的主客体定位．该研究[11]以参与培训期间教师间合作学习活动为主．一方面，来自当时学校数学课程的一系列代数问题的解决在培训中被强化学习；另一方面，教师教育者在选择这些问题的解决时也充分考虑该研究项目的研究聚焦点．Borko等[11]分析的数据片段基本聚焦教师教育者在培训期间建立教师专业学习团体的不同途径，及教师如何通过此学习团体的合作学习拓展教师的代数知识．该研究根据对培训前后的教师代数知识的测试和访谈，教师学习日记反思以及他们的培训结业报告的分析，提供的初步分析结果证实了该暑期培训对参与培训教师的职业成长有积极影响．

5 研究结论和讨论

表2总结了对以上3个数学（学科）教师合作学习模式的主要素及其关系、规模、学习理论、研究方法，及与研究背景的关系．

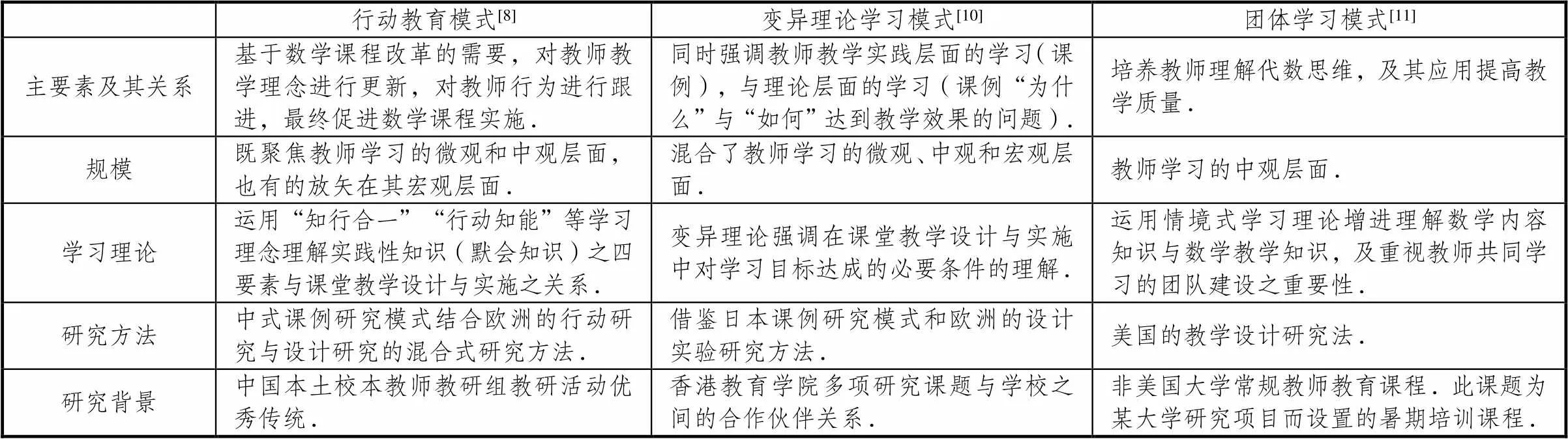
表2 比较分析3个教师合作学习模式的“主要素及其关系”“规模”“学习理论”“研究方法”“研究背景”

在此基础上，比较分析的主要结论如下：第一，以上3个数学（学科）教师合作学习模式的理论支撑虽然都参考一般化的学习理论（并非针对数学学科教学），研究的聚焦点都是考察数学（学科）教师的专业知识的习得与课堂教学行为改进这两个要素的关系，而非Boylan等[12]选取的一般教师学习模式中强调的关于教师信念与实践这两个要素间的关系；第二，混合不同的研究方法可以调动多种不同研究思维方式，实现方法的互动与融合，以拓展关于教师合作学习模式的主要素及其之间关系的多样性与复杂性的综合研究方法．

根据以上比较分析结论，下文进一步讨论ICMI Study 25所强调的数学教师如何通过运用合作学习模式，如何拓宽数学（学科）教师共同学习及其研究所需一般化和专业化学习理论的建设和研究方法的综合与创新．第一个方面是关于数学教师合作学习的研究所参考的西方理论与研究方法论，国内研究工作者与教师教育者在未来需要进一步在本土实践中重视对中西方不同研究思维方式的理解与运用．第二和第三个方面是关于研究学科（数学）教师合作学习的研究问题与方法的进一步思考方向．

（1）关于处理数学教师合作学习的研究设计与实践之间关系的西方学术研究的分析性思维方式（理论框架在先，研究设计、数据分析与实践在后）与中国文化特有的整体性思维方式（观察、实践、经验在先、理念诠释与理论提炼等在后）的理解与运用．

（2）促进大学研究工作者、各类专家、学校教师之间交流的多样性协调（cooperation）与合作（collaboration）．

（3）数学教师合作式教学研修及其研究是否需要强调其学科独有的默会知识？

关于第一方面，行动教育与变异理论学习模式都强调以课例学习为载体，采用备课、试教、评课、反思的循环式合作学习，以便教师更新知识，促进课堂教学质量．Morris和Hiebert[6]指出，课例学习的结果是一种教学产物．即它的潜在作用是指导教师教学行为跟进以帮助学生达成预定教学目标．另外，根据表2所示，这两个模式重视教师合作学习和知识更新的完整研修过程，即同时强调教师的课堂教学设计（备课）与教学设计的课堂实施操作（试教）．Huang和Shimizu[4]认为行动教育（即中日等国教师合作研修等多样性课例研修模式之一）和变异理论学习的实证研究都表明，此两个模式既可作为研究工具深入了解学习理论在教师教学中的应用性，也可考查教师的多轮循环教学实践如何为理论的提炼与补充提供实证数据．值得注意的是，Huang和Shimizu[4]的学习理论指导教师实践，实践进一步完善理论的观点反映了西方关于教师专业发展的主流研究重视理论框架在先，指导实践在后的分析性思维方式．Cobb等[18]的观点蕴含“分析性思维方式”，例如，从科研的实用性角度讲，教师专业发展研究旨在针对为帮助教师提高课堂教学质量提供精准专业知识指南．从学术理论角度讲，通过参与这类研究，研究者们通过不断的理论预设、实验测试、改进研究问题和研究方法等，以此了解教师专业发展过程中渐趋复杂精细的教学实践和与之发展相匹配的操作工具与支撑平台．

在此，研究者[7]强调须重视中国行动教育模式中倡导的科研工作者与实践者共同学习，并以此来处理理论联系实践的整体性思维方式与分析性思维方式的复杂关系．正如行动教育模式[8]所指出的，中国各级教研员在指导教师数学学科知识和其教学知识的学习中，倾向于首先联系具体教学案例的分析．而抽象化一般化的理论知识层面的剖析，是通过强调教师对此类专业知识的反思及行为跟进而循序渐进地理解与应用．研究者[8]考虑今后的研究应重视此中国特色的整体性思维方式，特别是中国文化特有的双向思维互动，即分析思维中有整体思维，整体思维中有分析思维（分中有合，合中有分）的研究思想与方法的建设．一方面重视探索如何在教师课堂教学实践中诠释和指导教师理解相关理论的整体性思维，另一方面应聚焦研究如何使课堂教学实践有针对性地接受理论指导与制约的分析性思维．重视教师针对教学理念的课堂行为跟进与进一步应用理论分析反思行为的双向思维互动的研究可以帮助国内教师克服理论联系实践的学习瓶颈，并促进教师运用其习得的专业知识与反思能力发展形成自己的课堂教学信念、理论与教学风格[3，5]．同时，也对中国建设有本土特色的数学教师教育理论积累丰富的实证研究数据与经验智慧．

第二方面，上面3个模式的初步分析结果引导在今后的科研工作中进一步思考如下研究问题．即教师专业发展的模式应聚焦“谁的知识”（如学生、教师、教研员、各类专家）？什么是某一模式所针对性地学习或研修？此学习或研修过程是如何呈现的？Kempe[5]突出强调研究者与教师之间合作不拘一格的形式议题．例如，教学任务设计以大学研究者为主导（如上所述的团体学习模式），而课例学习也可由教师主导（如国内校本教研活动）．Kempe解释课例模式重视教师与大学研究者合作，因为他们有共同的研究问题与目标．即课例研究中教师是研究伙伴，而非被研究者．课例研究聚焦研究者和教师共同关心的学习目标的构建知识与师生教学关系．行动教育与变异理论学习的模式都具有这些优势．教师的积极参与真实课堂的课例教学的合作研究被视为可弥补其理论与实践的差距[3，5]．尽管如此，如顾非石与顾泠沅[8]、Lo和Marton[10]、Borko等[11]、Huang和Shimizu[4]所述，专家学者的专业引领在上述3个模式中被证实．当下需要解决的瓶颈问题之一是上述3个模式在推广使用中，什么调整是必须的，以便职初或新老师在研修活动中容易上手操作学习[3]．针对教师合作学习过程中的主客体定位，可参阅ICMI Study 25的C组专题讨论问题的另一篇报道[27]，即运用Boylan等[12]的分析框架，分析了上海宋庆龄学校承担的市级课题“在变式教学与探索式学习理念指导下的数学课堂教学设计的课例研究”模式[3，21-22]和欧盟的数学与科学学科教师的合作模式及进一步研究议题．

第三方面，在开发新的研究课题设计中，非常重要的一点是：数据的收集方法须便于研究者解决在理解和诠释数学学科教师专业学习中学科（数学）教学实践与默会知识之间关系及推广研究成果的模式时所遇到的障碍[5-6，23]．数学教师合作式教学研修及其研究是否需要强调其学科独有的默会知识？例如，Marton[10]的变异理论，行动教育模式提倡的行动智慧，知行合一理念，团体学习模式中对情境式学习理论都是一般化的学习理论（并非针对数学学科教学），而顾非石与顾泠沅[8]关于教师指导者指导内容与指导方式的研究有一系列子问题尚待解决．这都表明对数学教师专业研修的各类知识界定，如数学学科知识、教学知识、实践性知识（默会知识）与舒尔曼的PCK等教师专业知识的分类之异同及相互关系，是一个尚待解决的学术问题[28-29]．这里选取的3名教师合作学习模式都侧重考察数学（学科）教师的专业知识的习得与课堂教学行为改进两个要素的关系，而非Boylan等[12]选取的一般教师学习模式中强调的关于教师信念与实践这两个要素间的关系．这里需要说明的是，研究者对所选文献不同研究问题的侧重，与所研究的教师学习模式和数学学科教师学习模式研究的广度和深度等不同研究维度相关．范良火[30]指出从20世纪80年代开始，国际数学教育学术领域就关注数学教师专业知识的3个主要研究问题：第一个问题是教师需要什么知识？第二个是教师具备什么知识？第三个是教师如何提升他们的知识？ICMI Study 25聚焦的是如何通过合作学习的途径拓展对第三个问题的学术讨论与研究．在今后研究中，研究者[7]认为不仅有必要进一步理解中国数学教师学科教学实践中所需的默会知识的本质，还需要对相关人士（研究者、教师、专家等）的（数学）学科教学的职业信念与态度，情感与思维方式做哲学范式层面的理论探索[12]．这对中国人建设有鲜明本土特色的数学教师教育研究的哲思体系与理论有重大意义．因为中国人在处理个人与他人、个人与集体、个人与社会等关系情境中的合作学习所体现的认知、行为、情感、信念、精神、道德、价值观等方面关系与西方不同，不能完全照搬西方的学习理论来分析诠释中国教师在本土传统文化教化下接受的“止于至善”的共同学习的理念、情怀、修养和致意．另外，3个模式的比较分析支持Boylan等研究者[12]关于以教师职业发展的各类模式为工具，富有弹性地操作使用的建议．即大学的研究人员必须提供一套关于适合中国教师合作学习模式的实用操作原理，为教师提供针对不同研修目的的各类合作学习模式为操作工具的使用指南，并提供专业学习的设计、评估及其研究的相关知识信息．

6 ICMI Study 25对建设中国数学教师合作学习理论与实践的意义

在ICMI Study 25的A组专题，各国研究者深入交流关于数学教师合作学习模式的理论及研究方法论．例如，“Documentary Genesis”“Semiosphere, Semiotic Mediation, Boundary Objects”“Cultural-Historical Activity Theory”“Expansive Learning”“Social Practice Theory / Figured Worlds”“Meta-Didactical Transposition”“Anthropological Theory of the Didactic”，等理论．在此仅提供这些理论的英文学术简称，供国内同行了解．具体的ICMI Study 25的A组专题组内报道可参考已出版的ICMI Study 25 Proceedings．ICMI Study 25学术书籍也正在出版准备阶段．如上文所述，不一一字面翻译．术语的界定与翻译是一件非常艰辛的工作．纯粹的字面翻译不仅可能有走样和失真的地方而令国内读者产生不必要的困惑，也有进一步加剧外来理论与本土传统实践的“夹生饭”问题．因为在翻译这些西方学术理论名词时，翻译者需要同时打通理论家与实践者所在不同学术与实践领域的双重语境的瓶颈问题：一个是西方学术理论名词术语如何丰富中国教师教育的已有理论专业术语与思维，以便进一步指导适合本国国情的实践与理论建设；另一个是这些外来学术理论名词如何有效地促进国内学校一线教师的工作交流，通过合作学习提升教师个体对数学课改、教改背后的理念的兴趣，进而追求与之匹配的教法学法的创新．这些新的外来理论名词能否与教师日常工作实践已有理论及教学评价交流等使用的语码相互联系，使教师在共同学习与研修中产生思想与情感的共鸣？能否提供给参与合作学习的教师一系列丰富的联想，使教师主动、可持续地自我学习、研究与课堂实践？

上文行动教育模式的介绍中，关于“学习理论”的阐述，涉及到“该模式体现了两个有中国特色的学习理念：一个是行动智慧；另一个是王阳明的知行合一理论”，这里的“学习理念”与西方的“学习理论”并非对等，尚需进一步诠释、分析、思辨．另外，涉及到的这两个理念并非数学教育学术研究领域中一般意义上的学习理论．这恰恰提醒大家应重视上文所述的中西方学术界主流的分析式思维与整体性思维之区别与加强建立此双向思维的互动与灵活应用的必要性．进而，考察数学教师教学研修及其研究是否需要强调其学科独有的默会知识的研究课题[28-30]．

当前在中国课改中，广大教师教育工作者和教师合作学习都面对双重挑战，即如何在更新所需的教育及学科教学理念的同时，继承并发扬中国中小学教师长期积累的教研研讨，共同学习的优秀传统和宝贵的实践经验与智慧．研究者作为一名曾在上海某中学任教近十年的一线数学教师和多年参与国内校本教研活动及研修的研究工作者，在国内教研活动中，经常听到的一句话是“实践出真知”．这句话到底蕴含着什么？在ICMI Study 25的A组专题组内报道的理论文献中，来自中国的理论知识并非主流．就教师课例研修的模式而言，国际学术界及校际间的共识也以日本教师的课例研修模式为主流．ICMI Study 25强调的教师“合作学习”与中国校本传统的教师教研活动共同学习，在互相讨论和交流中，提高每一位教师对教学的认识在理论层面有何异同？可喜的是，中国的行动教育模式、中式课例研究、校本教师的教研活动正被越来越多的外国学者与教师所接受并学习[19，31-32]．这更促使中国本土的研究工作者对“实践出真知”的真知做出中国的诠释和理解．值得注意的是，Boylan等[12]批判性地分析了5个关于教师学习的路径与过程的模式后，进一步提出未来研究教师学习模式具有4个方面的重要性：（1）针对教师学习过程及出现改变的诠释的研究理论相对不足；（2）应重视教师情境式学习的本质；（3）目前缺乏对教师作为一个活生生的学习个体与人的完整的终身学习成长的理论构建；（4）对教师的群体合作，共同学习的社会化维度的阐释．中国校本教师教研活动丰富，教师合作形式多种多样，教师的学习观更是接受中国传统儒、释、道等文化与学习经典理论的教化．因而，中国研究者可以对Boylan等[12]提出的以上课题进一步完善理论并创新研究方法．孔子《论语》中的“吾十五而有志于学”“见贤思齐”“三人行必有我师”等经典名言非常重要，且早已被中华民族所接受，被广大教师在共同学习研修中所接受．中国的学科教师教育研究不能不被重视．而《论语》等中国古典学习理论的学习并非死板地分门别类单指特指某一学科的书本知识学习，而是活泼的，以人为本，体现“合中有分，分中有合”思想的，生生不息的、多维度的整体学习观．“温故而知新，敦厚以崇礼”，这是对中国数学教师教育研究工作者今后在国际视野下的学术工作的期待．既要懂得西方理论的思想和方法，也要重视中国独特的优秀传统与实践智慧．这样，大家才能讲好中国故事，以中国经典学习理论的“经”注好本土教师共同学习研修积累的宝贵的经验智慧的“经”．

致谢：文章得到北京师范大学曹一鸣先生，华东政法大学丁海林先生帮助校对．文章是在与英国南安普顿大学Keith Jones先生合作的ICMI Study25的报告基础上，做理论与研究方法层面的进一步探讨与思考．特此一并致谢．

[1] CHEN X, ZHANG Y. Typical practices of lesson study in East Asia [J]. European Journal of Education, 2019 (54): 189-201.

[2] WOOD K. Is there really any difference between lesson and learning study? Both focus on neriage [J]. International Journal for Lesson and Learning Studies, 2017, 6 (2): 118-123.

[3] DING L, JONES K, SIKKO S A. Interconnectedness and difference between action research and a lesson design study in Shanghai, China [J]. Educational Action Research, 2019, 27 (4): 595-612.

[4] HUANG R, SHIMIZU Y. Improving teaching, developing teachers and teacher educators, and linking theory and practice through lesson study in mathematics: an international perspective [J]. ZDM Mathematics Education, 2016, 48 (4): 393-409.

[5] KEMPE U R. Teachers and researchers in collaboration: A possibility to overcome the research-practice gap [J]. European Journal of Education, 2019 (54): 250-260.

[6] MORRIS A K, HIEBERT J. Creating shared instructional products: An alternative approach to improving teaching [J]. Educational Researcher, 2011 (40): 5-14.

[7] DING L, JONES K. A comparative analysis of different models of mathematics teacher collaboration and learning [C] // BORKO H, POTARI D. Proceeding of ICMI Study 25 on Teachers of Mathematics Working and Learning in Collaborative Groups. Lisbon: University of Lisbon, 2020: 110-117.

[8] GU F, GU L. Characterizing mathematics teaching research specialists’ mentoring in the context of Chinese lesson study [J]. ZDM Mathematics Education, 2016, 48 (3): 441-454.

[9] 顾泠沅，王洁．教师在教育行动中成长——以课例为载体的教师教育模式研究（上）[J]．课程·教材·教法，2003，23（1）：9–15．

[10] LO M L, MARTON F. Towards a science of the art of teaching: Using variation theory as a guiding principle of pedagogical design [J]. International Journal of Lesson and Learning Studies, 2012 (1): 7-22.

[11] BORKO H, FRYKHOM J, PITTMAN M E, et al. Preparing teachers to foster algebraic thinking [J]. ZDM Mathematics Education, 2005, 37 (1): 43-52.

[12] BOYLAN M, COLDWELL M, MAXWELL B, et al. Rethinking models of professional learning as tools: A conceptual analysis to inform research and practice [J]. Professional Development in Education, 2018, 44 (1): 120-139.

[13] GUSKEY T R. Professional development and teacher change [J]. Teachers and Teaching: Theory and Practice, 2002, 8 (3): 381–391.

[14] DESIMONE L. Improving impact studies of Teachers’ professional development: Toward better conceptualizations and measures [J]. Educational Researcher, 2009, 38 (3): 181–199.

[15] CLARKE D, HOLLINGSWORTH H. Elaborating a model of teacher professional growth [J]. Teaching and Teacher Education, 2002, 18 (8): 947–967.

[16] OPFER V D, PEDDER D. Conceptualizing teacher professional learning [J]. Review of Educational Research, 2011 (81): 376–407.

[17] EVANS L. Leadership for professional development and learning: Enhancing our understanding of how teachers develop [J]. Cambridge Journal of Education, 2014, 44 (2): 179–198.

[18] COBB P, JACKSON K, DUNLAP SHARPE C. Conducting design studies to investigate and support mathematics students’ and teachers’ learning [M] // CAI J. Compendium for research in mathematics education. Reston, VA: National Council of Teachers of Mathematics, 2017: 208–233.

[19] 杨玉东，严加平．究竟什么是中式课例研究[J]．上海教育科研，2020（10）：38–44．

[20] 顾泠沅，朱连云．教师发展指导者工作的预研究报告[J]．全球教育展望，2012，41（8）：31–37，50．

[21] DING L, JONES K, PEPIN B, et al. An expert teacher’s local instruction theory underlying a lesson design study through school-based professional development [C] // LILJEDAHL P, NICOL C, OESTERLE S, et al. Proceedings of the Joint Meeting 2-401 of PME 38 and PME-NA 36. Vancouver: PME, 2014: 401–408.

[22] DING L, JONES K, MEI L, et al. “Not to lose the chain in learning mathematics”: Expert teaching with variation in Shanghai [C] // BESWICK K, MUIR T, FIELDING-WELLS J. Proceedings of 39th Psychology of Mathematics Education conference. Hobart: PME, 2015: 209–216.

[23] STIGLER J W, HIEBERT J. The teaching gap: Best ideas from the world’s teachers for improving education in the classroom [M]. New York: The Free Press, 1999: 1–225.

[24] BROWN A L. Design experiments: Theoretical and methodological challenges in creating complex interventions in classroom settings [J]. The Journal of the Learning Sciences, 1992, 2 (2): 141–178.

[25] COLLINS A. Towards a design science of education [M] // SCANLON E, SHEA T O. New directions in educational technology. Berlin: Springer, 1992: 15–22.

[26] LO M L, MARTON F, PANG M F, et al. Towards a pedagogy of learning [M] // MARTON F, TSUI A B M, CHIK P P M, et al. Classroom discourse and the space of learning. Mahwah: Lawrence Erlbaum Associates, 2004: 189–225.

[27] SIKKO S A, DING L. Roles of facilitators and teachers in models of teacher professional learning [C] // BORKO H, POTARI D. Proceeding of ICMI Study 25 on Teachers of Mathematics Working and Learning in Collaborative Groups. Lisbon: University of Lisbon, 2020: 548–555.

[28] KIRSCHNER P A, VERSCHAFFEL L, SRAR J, et al. There is more variation within than across domains: An interview with Paul A. Kirschner about applying cognitive psychology-based instructional design principles in mathematics teaching and learning [J]. ZDM Mathematics Education, 2017, 49 (4): 637–643.

[29] NEUBRAND M. Conceptualizations of professional knowledge for teachers of mathematics [J]. ZDM Mathematics Education, 2018, 50 (4): 601–612.

[30] FAN L. Investigating the pedagogy of mathematics: How do teachers develop their knowledge [M]. London: Imperial College Press, 2014: 1–366.

[31] YANG Y. How a Chinese teacher improved classroom teaching in teaching research group: A case study on Pythagoras theorem teaching in Shanghai [J]. ZDM Mathematics Education, 2009, 41 (3): 279–296.

[32] HUANG R, LI Y. Teaching and learning mathematics through variation: Confucian heritage meets western theories [M]. Rotterdam: Sense Publishers, 2017: 1–476.

[33] HUANG R, FANG Y, CHEN X. Chinese lesson study: A deliberate practice, a research methodology, and an improvement science [J]. International Journal for Lesson and Learning Studies, 2017, 6 (4): 270–282.

A Comparative Study of Theory and Practice of Mathematics Teacher Collaborative Learning

DING Li-ping

(Department of Teacher Education, Norwegian University of Science and Technology, Trondheim, Norway)

This paper examines the key components and their relationship, theoretical basis, and research methods and operations in three selected models of mathematics teachers’ collaboration and learning (MTCL) from Boylan et al.’s (2018) analytical framework of teacher professional learning models: the action-education model, the learning study model, and a community-centered model for teacher learning. The analysis shows that the design of the three models is largely based on general learning theories and ideas (not specific theories of mathematics subject teaching and learning). Noticeably, researchers have concentrated on the relationship between the nature of mathematics teachers’ professional knowledge for/in teaching and classroom practice to interpret teachers’ learning and changes. Moreover, researchers have applied multiple thinking processes underlying the interactions of different research methods in the three models. This comparative analysis highlights three significant aspects of developing Chinese mathematics teacher education theory and practice: (1) researchers and teacher educators in China need to be aware of differing ways of thinking and alternative research methods between China and overseas. (2) Research of MTCL needs to make clear whose knowledge is emphasized in MTCL. (3) Is it necessary to address the uniqueness of the tacit knowledge used in teaching mathematics in MTCL? It is important to explicitly consider the philosophical paradigms used in theorizing MTCL in China.

mathematics teachers’ collaboration and learning; research method and design principles; learning theory; teachers’ belief and practice; teachers’ knowledge and practice

2021–05–06

上海市教育科学规划课题；中国福利会与上海宋庆龄学校联合资助教师科研项目——在变式教学与探索式学习理念指导下的数学课堂教学设计的课例研究（B12144）

丁莉萍，女，吉林德惠人，副教授，博士，博士生导师，主要从事中小学数学教师教育，中小学生数学学习成绩与情感研究．

G40–03

A

1004–9894（2021）03–0004–08

丁莉萍．数学教师合作学习的理论与实践之比较分析[J]．数学教育学报，2021，30（3）：4-11．

[责任编校：周学智、陈汉君]