连续基数集合并集性质的探讨及翻转课堂教学注记

臧 睿

(东北林业大学 理学院，哈尔滨150040)

1 引 言

实变函数是数学与应用数学专业的主干课程，其在专业培养乃至后续研究生学习中的基础作用不可忽视.从这门课程开始，此前数学分析、解析几何等课程中限定在n空间中讨论的定义和性质将逐步扩展到各类抽象空间中来讨论.因其对学生的抽象思维，逻辑思维提出更高的要求，久之便产生“实变函数学十遍”的传说，这也从侧面说明该课程的学习需要付出更多的时间和精力.随着高等教育改革的深入进行，各高校对课程设置比例和毕业学分要求进行了调整，为适应要求，很多课程的学时进行了压缩，因此对课程内容设计、教学模式以及教材结构提出了新的要求，多位学者[1-5]对此进行了探讨和研究.文献[6]一直是作者任教专业的实变函数、泛函分析课程教材，因其结构严谨，逻辑清楚，难易适度，也被很多高校广泛采用.在近些年的教学中，为应对学时不足的困扰，在课程内容和教材结构方面进行了一些思考和探索.例如连续基数，多年教学实践表明集合的基数是学生刚开始学习实变函数时接受较为困难的部分.由于对正整数集非常熟悉，因此学生对可数集合往往理解较好，接受较快，但对连续基数的一些结论往往感觉较为抽象，例如连续基数集合的并集.本文结合连续基数集合并集性质的证明，浅谈一些思路和方法.

2 连续基数集合并集性质注记

以下用c表示连续基数.关于c个基数为c的集合的并集，文献[6]中第一章第五节推论2表述为：“设有c个集的并集，若每个集合的基数都是c，则其并集的基数也是c”.对此结论教材中解释为：“对每一个被并的集，使之与平面xOy上平行于Ox轴的直线上全体点所成集合作成一一对应，也就得到所述的并集与平面xOy上全体点所成集合作成了一一对应”.对此解释会产生的一个疑问是当集合互不相交时，这样的一一对应是比较明显的，但当集合相交非空时，这样的解释就会较为含混.比较文献[6-14]，发现不同教材对类似内容的处理和表述不尽相同，文献[7-10]中未列出相关结论，文献[11-12]中的结论针对互不相交集合的并集，文献[13]定理1.3.5表述为：“c个基数为c的集合之并基数为c”，在其证明中首先指出不妨假设集合互不相交，随后对相交的情况进行了详细证明.可见对该结论证明的一般处理是对互不相交的情况进行阐述，之后再推广到一般情况，进行讲解时用时较多.文献[14]推论1.2.6给出了一般情况的直接证明，相比较而言更为简洁，但文中叙述较略，学生首次学习理解较为困难.下面给出一种较为详细的直接证明的处理方法.这种方法可以直接涵盖文献[14]推论1.2.6中关于可数多个和c个基数为c的集合并集的两个结论的证明.

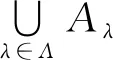
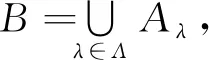
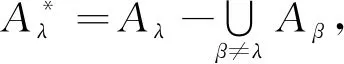
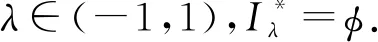
3 翻转课堂教学案例设计

近年来，翻转课堂教学模式受到广泛关注，如果设计合理，也可以提升课程教学的效率.数学课程的特点决定其不适宜进行大学时比例翻转课堂教学[15]，但在适当环节，结合适当内容进行翻转课堂教学可以有效激发学生的思想活力，加深对课程内容的理解.以下是关于翻转课堂方案设计的一些思考.

完备集与完备度量空间是度量空间中的重要定义，教学实践中，很多学生容易将二者混淆.完备集是没有孤立点的闭集，完备度量空间是指任何柯西点列都在空间中收敛，从定义描述的角度看，学生能理解二者的不同，但对二者联系的理解往往不够深入.这里可以给出由浅到深的几个问题，引导学生逐步理解这两种定义的区别和联系.

问题1：完备集和闭集的关系是什么？问题2: 度量子空间完备与闭的关系是什么？问题3： 空间完备和空间本身为完备集的关系是什么？

问题1主要考察完备集的定义，完备集为没有孤立点的闭集，因此完备集一定为闭集，反之引导学生举出含孤立点的闭集的例子即可说明闭集未必为完备集.问题2主要考察学生对相关定理的熟悉程度，即度量空间的完备子空间为闭子空间，当空间完备时，闭子空间一定是完备的，当学生指出空间不完备时，闭子空间是否仍是完备的，即任意度量空间的子空间的完备性与闭性等价是否成立，可以给出以下反例：

例2考虑有理数集，度量为d(x，y)=|x-y|，此时空间(，d)不完备，令M=∩[a，b]， 则M为闭集，但不完备.

由此引导学生梳理出两个定义的联系：对于完备度量空间，完备集为完备子空间，完备子空间只是闭集，因此未必为完备集；对于一般度量空间完备集也未必为完备子空间.以上讨论的子空间的完备与闭集或完备集的联系，接下来可以提出问题3由学生思考，事实上例2的空间本身(，d)是完备集，但空间不完备，这说明空间本身为完备集与空间是否完备无关.

4 结 论

通过比较不同实变函数教材，梳理了连续基数并集性质的不同处理方式并得出相对高效的证明方式，说明结合不同教材的特点，深挖细究确实可以部分克服学时不足带来的困扰.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.