可变供给压力阀控制的机械臂节能方法

张淑坤，郭 娟，李 成

（1.新乡职业技术学院机械制造系，河南新乡453000；2.安徽理工大学机械工程学院，安徽淮南232001）

传统机械臂大多采用电机与减速器相结合的方式，导致机械臂功率与体积比较小，输出的力矩较小。相比电机传动，液压传动具有负载大、运动平稳、结构紧凑及节约能量等优点［1-2］。液压传动可以通过调节压力大小，进而达到控制输出功率的目的。机械臂关节结构通常较长，在工作过程中难免发生颤振，对控制系统的稳定性造成很大的干扰，进而造成末端执行器运动轨迹定位误差较大。目前，机械臂大多采用液压驱动技术，但是控制系统精度还有待于提高。因此，科研工作者不仅要研究机械臂液压驱动方式，而且还要设计出高精度和稳定性较好的控制系统。只有这样，才可以适应时代发展的需要，才不会被社会所淘汰。

当前，为了提高机械臂运动关节角位移精度，国内外许多学者对机械臂运动轨迹展开了研究。例如：文献［3-4］研究了机械臂液压伺服系统的自适应模糊控制方法，建立机械臂液压驱动模型，利用参数自适应算法预测控制系统未知参数，采用非连续投影算法确保预测参数的有界性，通过仿真验证跟踪误差大小，从而提高机械臂轨迹跟踪精度。文献［5-6］研究了液压机械臂运动轨迹神经网络控制系统，创建了液压柔性机械臂空间结构，对机械臂系统进行参数化设计，一阶梯度法搜索机械臂运动期望位置，实验验证机械臂轨迹跟踪效果，提高了机械臂控制系统的响应速度。文献［7-8］研究了液压伺服驱动机械手运动轨迹改进神经网络PID控制方法，建立了机械手平面简图，推导出机械手运动空间数学关系式，采用改进粒子群算法对神经网络PID控制器参数进行优化，通过仿真验证机械手末端执行器输出误差，提高了机械手末端执行器运动轨迹控制精度。以往研究的机械臂运动轨迹控制精度虽然有所提高，但是，机械臂消耗的能量较多，从而造成资源的浪费。对此，本文建立了可变供给压力阀控制驱动装置示意图，推导出液压驱动方程式。为了降低机械臂运动系统能量消耗，设计了前馈反馈控制模式，最后通过Matlab软件对机械臂运动关节角位移跟踪、供给压力和电机转速进行仿真验证，与定量供给压力阀控制系统形成对比，为深入研究机械臂运动轨迹精度和节约能量提供参考。

1 压力阀控制系统

1.1 定量供给压力阀控制系统

定量供给压力阀控制（Fixed Supply Pressure Valve-Controlled，FPVC）液压驱动系统将用作基准。在这种系统中，通常使用PI控制器进行闭环位置控制。泵的转速通常是恒定的，并且必须足够高，以满足所有执行器组合的峰值流量要求，或者满足安装蓄能器时的平均流量要求，溢流阀使压力保持恒定，如图1所示。

图1 定量供给压力控制Fig.1 Control of quantitative supply pressure

1.2 可变供给压力阀控制系统

可变供给压力阀控制（Variable Supply Pressure Valve-Controlled，VPVC）系统的液压回路如图2所示，可以使用多个数量的阀门执行器，此处仅显示2个。单台定量泵由伺服电机驱动，每个控制阀都是调节阀，即比例阀或伺服阀。

图2 双执行器装置的液压回路Fig.2 Hydraulic circuit of dual actuator device

闭环阀阀芯位置控制和伺服电机速度控制可以在相关设备上实现。可变供给压力阀控制器必须生成马达转速指令和控制阀滑阀位置指令。控制器由两部分组成：前馈部分和反馈部分。对于具有N个致动器的多轴系统，给定所需的运动要求（yd1，yd2，…，ydn），前馈部分使用逆模型，能够预测所需的马达速度（ωm）和阀芯位置（x1，x2，…，x n）的命令。VPVC反馈部分通过比例积分控制器测量的位置（y1，y2，…，y n）调整前馈命令信号，如图3所示。

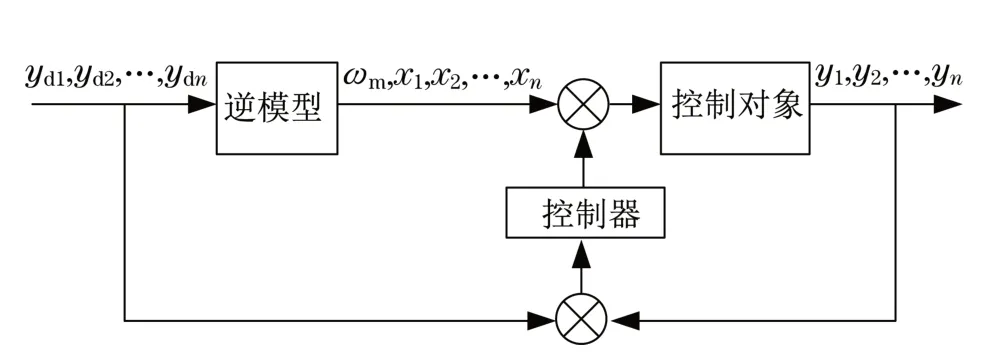
图3 VPVC控制算法Fig.3 VPVC control algorithm

2 前馈反馈控制设计

2.1 前馈控制

前馈部分预测所需的电机转速以及两个阀的相应滑阀位置，从而达到所需的最小供应压力PSi。对于具有给定运动需求的每个执行器，VPVC前馈部分使用两种不同的假设计算所需的供给压力：POi是控制该执行器阀门完全打开时所需的供给压力；PCi是当执行机构推力室中的压力达到无气穴临界值时所需的供给压力。

所需最高供给压力的执行机构被选为主执行机构（Master Actuator，MA），所需的MA供给压力是整个系统的最终所需供给压力PS，然后用此PS重新计算其他执行机构的阀门指令。电机速度指令由所有执行机构的总流量要求计算得出，对于给定要求运动的单个执行器，POi和PCi的预测是一个关键步骤，具体描述如下。

（1）完全打开阀门所需的供应压力（POi）。

在执行器i的延伸过程中，回流管在压力Pbi下连接到活塞有杆侧腔室，供应管在压力Pai下连接到活塞无杆侧腔室。其流量方程式［9］为

式中：Qai为无杆侧腔室流量；Qbi为有杆侧腔室流量；Aai为无杆侧腔室活塞截面积；Abi为有杆侧腔室活塞截面积；vi为活塞移动速度。

通过阀门的压降方程式为

式中：Pri为回油压力。

阀孔方程式为

式中：KVi为阀门常数；xi为阀门宽度。

考虑阀门完全打开时的情况，即xi=xOi，从式（3）和式（5）可知，回流压力Pri来计算Pbi，Pai可通过如下公式求得：

最后，根据式（2）和式（4），可以估计所需的供给压力，即

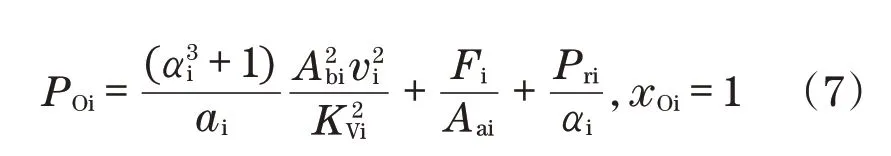
式中：αi为面积比Aai/Abi。

在执行器i缩回过程中，回油管在压力Pai下连接到活塞无杆侧腔室，供应管在压力Pbi下连接到有杆侧腔室。因此，通过阀门的压降可以表示为

如果阀门完全打开，即xOi=-1，则使用与延伸相似的推导，可以预测缩回期间所需的供应压力为

（2）避免气穴所需的供应压力。

在超负荷运行时，即当负载力Fi在伸出过程中为负或在缩回过程中为正时，推力室（伸出时的活塞无杆侧室和缩回时的有杆侧室）可能出现气穴现象。解决这个问题的办法是增加供给压力和减小阀门开度。计算程序是在推力室中施加等于最小阈值Pti的压力，并根据运动需求计算所需的供应压力（PCi）以及相应的阀门开度。

当延伸时，供给管连接到活塞无杆侧腔室，其处于最小阈值压力Pti计算式为

当缩回时，供给压力连接到有杆腔室，杆室被最小阈值压力Pti的计算式为

（3）非MA阀开度及电机转速计算。

在找到整个系统的供应压力和MA的阀门开度后，必须确定其他执行器（非MA）的阀门位置。如果需要延长非MA执行机构，其阀门开度［10］由以下给出：

当供给压力已经确定，并且每个执行器的给定期望流量下，可以计算所需的电机转速

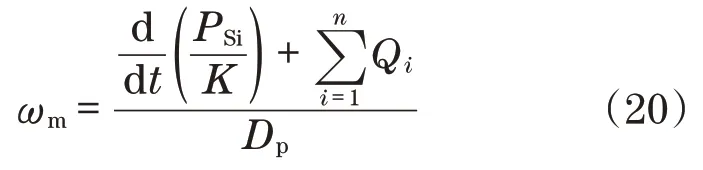
式中：K为供油软管内机油的有效刚度；Dp为泵的排量。

2.2 反馈控制

来自主执行器的位置反馈用于调整电机转速和液压油的流量。使用比例（P）控制器，比例增益乘以MA的阀芯位置信号。该方法考虑了阀门施加的执行器流动方向。因此，电机速度指令［11］为

式中：Kλ为电机转速调节系数。

执行器位置反馈用于使用比例积分（PI）控制器调整相应的阀门位置命令。所以阀门位置命令为

式中：s为微分算子；KP为比例系数；KI为积分系数。

3 结果与分析

3.1 液压机械臂模型

为了更好地分析液压执行器，以机械手驱动为例，其简图如图4所示。根据拉格朗日分析可知，肩关节和肘关节所需的力矩q1和q2分别［12］为

图4 液压机械臂Fig.4 Hydraulic mechanical arm

式中：I1、I2、I3分别为Pm1、Pm2和P3的重心惯量；L1为P1和P2之间的距离；L2为P2和P3之间的距离；C1为P1和Pm1之间的距离；C2为P2和Pm2之间的距离；M1、M2和M3分别为上臂质量、前臂质量和机械手的质量；θ1、θ2分别为肩关节和肘关节的角位移。

执行机构驱动力F1和F2的计算公式为

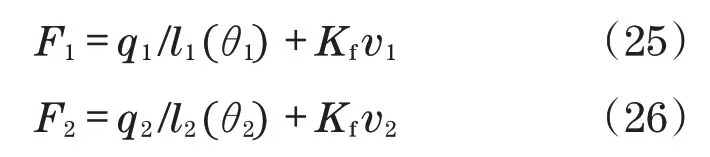
式中：l1（θ1）、l2（θ2）为执行机构杠杆臂长度；Kf为黏性阻尼系数；v1和v2为执行器的速度。

3.2 仿真及分析

为了验证可变供给压力阀驱动的机械臂节能输出效果，采用Matlab软件对液压机械臂关节角位移跟踪误差、供给压力和电机转速进行仿真，并且与定量供给压力阀控制结果进行对比和分析，仿真参数设置如下：泵的排量Dp=3.5 cm3/r；活塞面积Aai=2.2 cm2，Abi=1.4 cm2；PI控制调节系数KP1=120，KI1=20，KP2=140，KI2=40；角 位 移变化轨迹为θ1=-40+40cos（πt），θ2=120+40cos（πt）；仿真时间为t=6 s。肩关节和肘关节的角位移跟踪误差如图5和图6所示。供给压力变化如图7所示，电机转速变化如图8所示。

由图5和图6可知，机械臂控制系统采用可变供给压力阀驱动，肩关节角位移跟踪最大误差0.5°，肘关节角位移跟踪最大误差为0.7°。采用定量供给压力阀驱动，肩关节角位移跟踪最大误差1.2°，肘关节角位移跟踪最大误差为1.4°。由图7可知，机械臂控制系统采用可变供给压力阀驱动，供给压力稳定后变化主要在2 000~4 000 k Pa范围之内，采用定量供给压力阀驱动，供给压力稳定后变化主要在4 650~5 350 k Pa范围之内。由图8可知，机械臂控制系统采用可变供给压力阀驱动，电机转速主要在500 r/min以内，而采用定量供给压力阀驱动，电机转速主要在1 000 r/min左右波动。

图5 肩关节角位移跟踪误差Fig.5 Angular displacement tracking error of shoulder joint

图6 肘关节角位移跟踪误差Fig.6 Elbow joint angular displacement tracking er ror

图7 供给压力变化曲线Fig.7 Cur ve of supply pressure

图8 电机转速变化曲线Fig.8 Curve of motor speed change

因此，在同等条件下，采用可变供给压力阀驱动系统，机械臂跟踪误差较小，能够提高控制系统的运动精度。供给压力和电机转速较小，功率消耗较少，能够降低能量消耗，效果较好。

4 结论

针对机械臂运动关节角位移跟踪误差较低、能量消耗相对严重问题，设计可控供应压力阀控制系统，通过仿真检验输出效果，主要结论：①机械臂采用定量供给压力阀控制系统，机械臂运动关节角位移跟踪误差较大，能量消耗较多。而采用可变供给压力阀控制系统，机械臂运动关节角位移跟踪误差较小，能量消耗较少。②可变供给压力阀控制系统采用前馈反馈控制器，可以通过PI调节控制参数进行在线调整，提高控制系统的反应速度，降低机械臂运动轨迹输出误差，效果较好。③采用Matlab软件检验机械臂运动关节角位移跟踪误差、能量消耗，为设计人员提供参考数据，使机械臂控制系统设计更加合理，提高机械臂控制系统设计效率。