3-SPS/S踝关节康复机构模糊自适应控制系统仿真

王海芳，陈晓波，焦 龙，张 瑶，李新庆，朱亚锟

（东北大学秦皇岛分校控制工程学院，河北秦皇岛066004）

在人体的诸多关节中，踝关节占有至关重要的地位［1］。它在人行走、奔跑、跳跃过程中起到稳定平衡的作用，是人体主要承载关节，同时它也是人体下肢关节中比较容易损伤的部位。在当代快节奏的日常生活中，人们踝关节的损伤比例正在逐步增加，所以及时对患者进行有效的治疗和康复训练是非常必要的。传统的踝关节康复训练大多数是由康复医师进行接触式的辅助康复训练，患者被动训练，方式单一，医师工作量大导致训练时间较短，患者的康复周期较长。其次，人工辅助康复训练没有反馈机制，只能依靠医师经验，训练没有针对性，导致康复期进一步延长。随着现代科学技术的高速发展，踝关节康复机器人替代传统康复医师对患者进行踝关节康复训练将会得到广泛的应用。

所 提 的3-SPS/S（S：Spherical，球 副；P：Prismatic，移动副）踝关节并联康复机构是一个多输入多输出的复杂不确定性系统，具有时变性、非线性以及强耦合等特点［2］，而且在整个机构运动中，由于每个驱动杆的期望位移是通过位置反解求得的，所以有时会出现差异，甚至结果相差很大。因此，传统的控制方法不是十分精确。所研究的踝关节并联康复机构的难点在于同时控制三个驱动杆的长度来实现动平台的空间轨迹。目前，并联机器人的控制方法主要有比例积分微分控制［3］、自适应控制等。在精度没有要求的条件下，可以使用传统PID控制器。PID控制器可以分为两类［4］：第1类是PID参数在整个控制过程中不变，其缺点是当控制系统具有较高非线性且严重耦合时，PID控制器的性能将大大降低；第2类是自整定PID，可以在线更新PID参数。当操作范围变化时，则需要利用非线性控制理论重新调整PID控制器［5］。因此，提出了用模糊自适应PID控制踝关节并联康复机构，从而得到更好的控制精确。

1 3-SPS/S踝关节并联康复机构运动学模型设计

1.1 3-SPS/S并联康复机构设计

踝关节解剖轴如图1（a）所示，通过对踝关节结构的研究可知，踝关节可视为一个具有3个转动自由度的球关节，主要有3种基本运动：围绕z轴进行反复旋转的内旋/外旋运动、围绕y轴进行反复旋转的背屈/跖屈运动和围绕x轴进行反复旋转的内翻/外翻运动，旋转轴x、y、z如图1（b）所示。从机构学角度上讲，踝关节的康复训练实际上是踝关节绕3个互相垂直相交的坐标轴旋转运动，为满足踝关节康复训练的要求，可采用3-SPS/S并联机构。3-SPS/S并联机构是一种典型的空间3自由度转动的并联机构，主要由动平台、静平台、驱动杆支链和支撑杆4部分组成，如图1（c）所示。中间为支撑杆，支撑杆下端固定在静平台中心位置，上端通过球铰与动平台中心位置相连。结构中下平台是静平台，上平台是动平台，上下平台之间用3根可变长度的驱动杆通过球铰来连接，驱动杆本身可由电机控制实现伸缩，通过改变每个驱动杆的长度来实现动平台绕x、y、z3个轴的转动，从而得到动平台的空间驱动轨迹。结合上文分析使用Solid Works三维制图软件绘制3-SPS/S并联机构模型，如图2（a）所示，搭建起的整个踝关节康复机器人实验平台如图2（b）所示，通过电机控制驱动杆的伸缩，完成平台在3个自由度上的旋转，实现对踝关节的背屈、跖屈、内旋、外旋、内翻、外翻运动的康复治疗。

图1 踝关节结构模型及结构简图Fig.1 Ankle joint structure model and structural diagram

图2 机构三维模型及实验平台Fig.2 Institutional 3D model and experimental platform

1.2 3-SPS/S并联康复机构位置分析

在实际操作中，由于驱动杆存在角度约束问题，所以在康复训练过程中需要对3-SPS/S并联康复机构进行位置分析，使驱动杆转动的角度得到合理的控制，所用的康复机构是并联机构，与串联机构不同的是，并联机构的正解可能存在多个，比串联机构的正解要复杂的多，所以一般用位置反解进行位置分析。因此，通过位置反解对3-SPS/S并联康复机构进行位置分析，获得输入输出构件的关系。如图1（c）所示，在动平台上建立动坐标系oxyz、静平台上建立静坐标系o-xyz，且坐标原点均位于平台中心点。动平台外接圆半径为r，静平台外接圆半径为R。假设B mi为Bi点相对于静平台坐标系o-xyz的相对坐标值，B Bi为Bi点的绝对坐标值，ABi为Ai点的绝对坐标值。动平台和静平台中心点的距离为h。动平台按绕z轴、y轴、x轴的顺序转动，角度分别为γ、β、α。由图可知，各点的坐标如下：

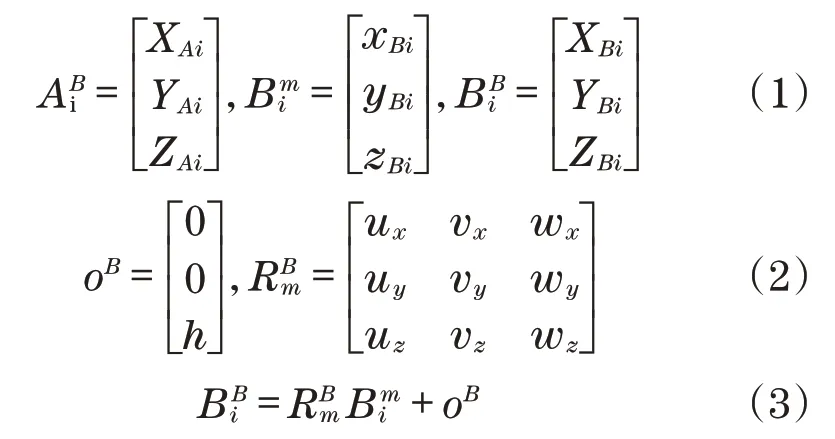
式中：为坐标系｛m｝到坐标系｛B｝的旋转变换矩阵。

若已知动平台的转动角度，即α、β、γ的值，即可求得每个支链L i的长度。通过减去初始状态各个支链的长度L i，得到驱动杆长度的变化量。

2 控制系统的设计

2.1 控制系统框图

SimMechanics是Matlab软件下的一个机构系统模块集，通过对各种运动副连接的刚体进行建模与仿真，实现对机构系统的动态性能分析与设计，达到实时分析和模拟显示机构运动状态的目的［6-8］。基于SimMechanics机构建模有两种方式：一种是直接利用系统中的模块集进行建模，该方式虽然建模过程简单，但模块参数设置复杂，容易出错［9-10］；另一种是借助实体建模工具及其与SimMechanics的接口技术实现联合建模，该方式根据建立好的三维模型自动设定模块属性，特别适用于复杂模型［11］。

基于机构平台的复杂性所以采用第2种方式建模，首先借助Solid Works软件建立3-SPS/S踝关节并联康复机构的三维模型；然后通过SimMechanics Link插件将建立的三维模型转换成Matlab/SimMechanics可视化模型；最后对模型添加驱动和传感器模块，即可建立3-SPS/S踝关节并联康复机构的控制框图，如图3所示。3-SPS/S踝关节并联康复机构仿真平台由5部分组成，其中轨迹生成模块（leg trajectory）的主要作用是通过反解动平台的期望位姿得到各支链运动轨迹；控制器模块（fuzzy PID controller）的主要作用是根据反馈的偏差产生算法控制量，实现对系统控制的目的；3-SPS/S并联康复机构模块（3-SPS/Splatform）的主要作用是作为被控对象接收算法控制量并作出相应的运动；轨迹跟踪模块（trajectory tracking）的主要作用是对空间中动平台运动轨迹进行分析，验证运动的正确性；传感显示模块（scope）的主要作用是对动平台相应的位置、速度以及误差信息进行检测并显示。

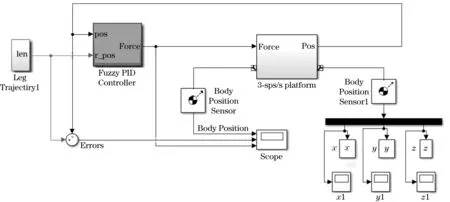
图3 控制系统框图Fig.3 Control system block diagram

2.2 控制器的设计

由于传统PID控制其参数调整的不确定性，会导致控制过程中的工作量增加，无法取得最佳控制效果［12］。而自适应控制是在系统的输入或干扰变化较大时，系统能够自动调节参数和控制策略，达到控制系统对输出量的要求，自适应控制是处理具有“不确定性”的系统的最好办法，通过观测不确定变量状态设法降低这种不确定性。所以将传统PID控制器和模糊逻辑相结合，组合成模糊自适应PID控制器。将驱动杆期望位移和实际位移的偏差量e以及偏差量的变化率ec作为输入量，比例系数增量Kp、积分系数增量Ki和微分系数增量Kd做为输出量，按照相对应的模糊规则建立一个两输入三输出的模糊自适应PID控制器。其中e的论域设为｛－0.3，0.3｝，ec的论域设为｛－0.3，0.3｝，Kp的论域设为｛－300，300｝，Ki的论域设为｛－15，15｝，Kd的论域设为｛－3，3｝，其中语言值均为｛NB，NM，NS，ZO，PS，PM，PB｝。算法原理如图4所示。

图4 模糊自适应PID算法原理Fig.4 Principle of fuzzy adaptive PID algorithm

以相应的模糊运算规则为依据，将控制系统输出的结果经过反模糊得到清晰量之后代入如下公式：

式中：Kp0、Ki0、Kd0为PID控制器的初始值；ΔKp、ΔKi、ΔKd为3个控制参量的修正值。

该算法最大的优势是不破坏原有常规PID的控制效果，仅依据系统的跟踪误差对PID参数进行增量调节（增量可正可负［13-14］），使PID的参数根据不同的偏差e和偏差变化率ec，实现在线修改。根据Kp、Ki、Kd3个参数的控制规则表，在Matlab的模糊工具箱里建立对应的模糊规则，完成模糊自适应PID控制器的设计。设计的模糊自适应PID控制器，如图5所示。

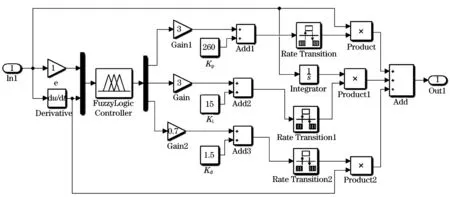
图5 模糊自适应PID控制器Fig.5 Fuzzy Adaptive PID Contr oller

3 仿真结果与实验验证分析

3.1 仿真结果分析

研究所选3-SPS/S踝关节并联康复机构参数如下：动平台半径r=125 mm，静平台半径R=160 mm，动平台和静平台之间支撑杆的长度h=500 mm。经过多次试验，按照控制效果取PID控制器的初始参数为：Kp=600，Ki=10，Kd=3.5。设动平台的运动轨迹输入为一个绕x轴，幅值为30，采样周期为0.005 s的正弦曲线。通过运动反解编写轨迹生成程序，得到各个驱动杆轨迹曲线，如图6所示（由于绕x轴运动时两个驱动杆运动相同，故驱动杆2和驱动杆3轨迹曲线重合）。

图6 驱动杆轨迹曲线Fig.6 Tr ace cur ves of drive r ods

为了证明提出的模糊自适应PID控制对3-SPS/S踝关节并联康复机构控制的优越性，在Matlab/Simulink中分别建立传统PID控制仿真和模糊自适应PID控制仿真，并对仿真结果进行比较。图7为系统的仿真结果，表1为模糊自适应PID控制器和传统PID控制器在幅值、超调量和调节时间方面的对比情况。结果表明，在相同参数情况下，模糊自适应PID控制的引入使得3-SPS/S踝关节并联康复机构在控制精度和动态响应方面都得到了改善。

表1 仿真及实验结果Tab.1 Results of simulation and experiment

图7 仿真结果Fig.7 Simulation results

3.2 实验验证

为了验证所提模糊自适应PID控制器的可行性，在搭建好的平台上进行实验验证。实验主要是无人的空载运行实验，测试在没有负载的情况下该装置是否可以完成康复训练以及角度精度误差是否在允许范围内。图8所示分别为零位、背屈角度为30°、外翻角度为30°、内旋角度为20°情况下的动平台位姿状态。

图8 并联机构位姿Fig.8 Position of parallel mechanism

在模糊自适应PID控制器的控制下，对装置进行多次实验，选取实验过程中误差最大的一组数据，数据如表2所示。数据表明，得到角度精度误差绝对值在1.0°以内，具有较高的控制精度。而实验平台在传统PID控制器的控制下的精度误差在3.0°以内，可知模糊自适应PID控制器提高了系统的控制精度。

表2 并联机构转角Tab.2 Results of simulation and experiment

4 结语

针对3-SPS/S并联康复机构难以实现高精度及快速响应的问题，设计了一种模糊自适应PID控制器，并在此理论基础上，进行仿真实验和结果分析。结果表明，模糊自适应PID比传统PID控制具有更好的动态响应性能，并且提高了控制系统的控制精度，为并联康复机构控制策略的研究提供了新的控制方法。