一类食饵具有收获率的带功能反应的捕食模型定性分析

张蓬霞

（长治学院 数学系，山西 长治046011）

本文研究了一类具有HollingⅢ型功能反应函数且食饵均常数收获率的捕食模型：［1-5］

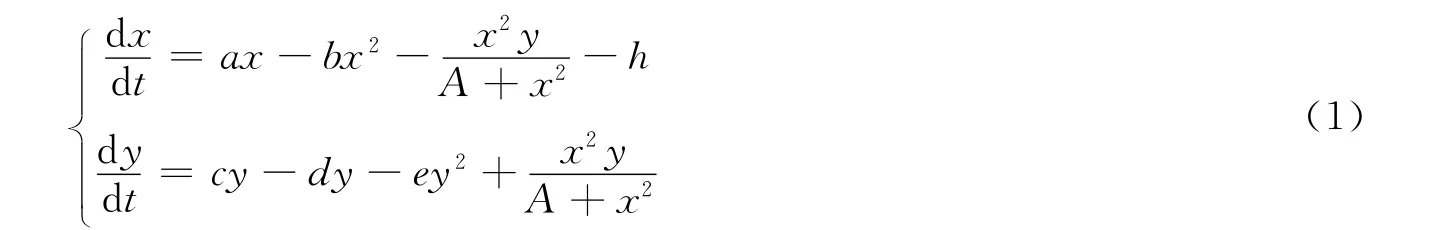
其中x，y表示两种群的密度，a，b，c，d，e均为正常数，模型中食饵具有常数收获率h.

1 模型建立

作变换dt=（A+x2）dτ，变换后仍记作x，t则有：

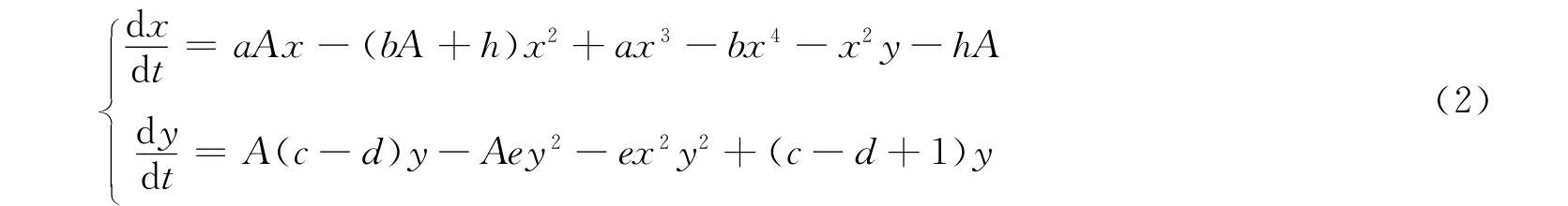
由模型（2）可知食饵等倾线为：

另捕食者等倾线为：

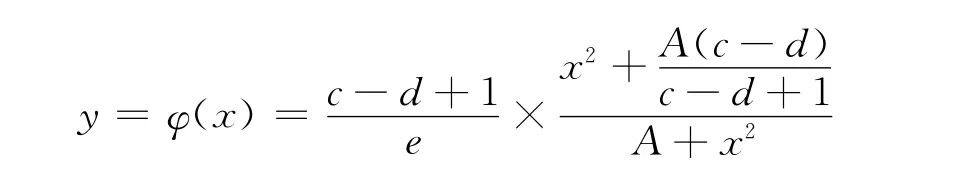
结论1若模型（2）的各参数满足，那么模型（2）有唯一正平衡点（u，v）.

2 模型平衡点与极限环问题

2.1 正平衡点稳定性

将模型进一步整理得：

设（u，v）是模型（3）的正平衡点，该点处线性近似方程的系数矩阵为：

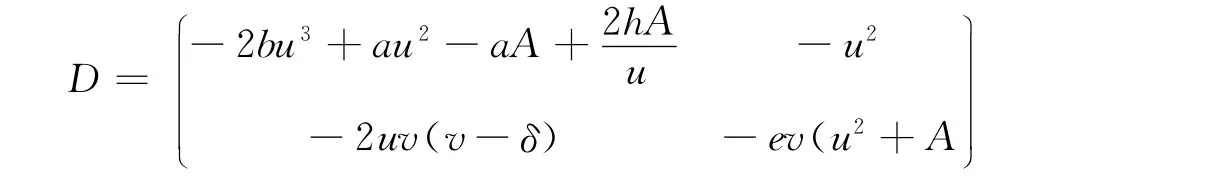
系数矩阵的迹为：

系数矩阵的行列式的值为：

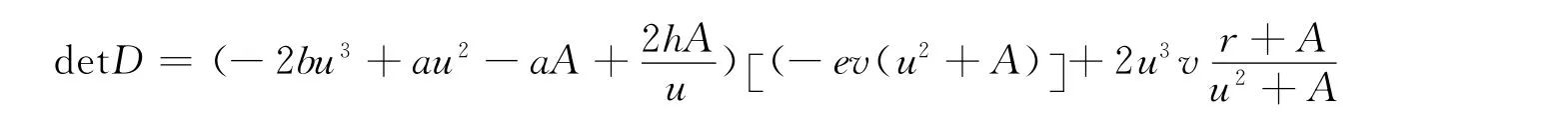
结论2若模型（3）各个参数满足结论1的条件，则正平衡点渐近稳定.

2.2 极限环不存在条件

结论3当满足2c-2d+1＜0时平衡点周围不存在极限环.

证：取Dulac函数B（x，y）=xmyn，容易算得：

2.3 无穷远点

由P＊（α，0）=-α（-b+eα）=0得α=0或是模型（4）的奇点.

对Q1（0，0）有则Q1不稳定.

那么q2=-b2＜0，则点为鞍点.