基于模型预测控制的风电场无功电压协调控制策略
2021-07-08鲍金雨李世华
鲍金雨,徐 龙,马 炯,陈 宁,3,李世华*
(1.东南大学自动化学院,南京 210096;2.中国电力科学研究院有限公司,南京 210003; 3.新能源与储能运行控制国家重点实验室,南京 210003)
风电的大规模并网对电网电压的稳定性影响越来越大[1].为应对并网点电压波动问题,风电场须具备一定的无功支持能力,并通过控制算法协调各无功补偿装置输出无功功率来支撑并网点电压.风电场调压方式繁多,其中备受关注的是通过单一或多种特性的无功补偿设备[2-5]建立多层次电压协调控制模型,利用灵敏度系数进行无功功率分配.该方式仅基于系统当前状态而未考虑不同时间尺度设备间的协调和未来状态的影响,故常出现控制滞后等问题[6].模型预测控制(model predictive control,MPC)作为一种优化控制算法,能够充分利用被控对象的模型信息,在当前状态基础上预测系统未来的输出,从而实现有限时间段内的最优控制.目前,MPC已能成功应用于新能源发电和微电网的无功设备协调调度[7-8].张哲[9]、肖浩[10]和Zhao[11]等分别建立了风机、静止无功补偿器(static var compensator,SVC)在无功控制下的数学模型,并基于MPC控制算法进行协调控制.张忠[12]、Zhao[13]和Guo[14]等则考虑有功功率的影响,采用了基于MPC的有功无功联合优化调度方法.本文拟基于模型预测控制算法进行风电场无功补偿控制系统的电压协调控制,通过设计扰动观测器(disturbance observer,DOB)对扰动进行估算,将扰动估计值引入预测模型削减扰动所致影响,以期提高系统的抗干扰能力.
1 协调控制的数学模型
1.1 风机
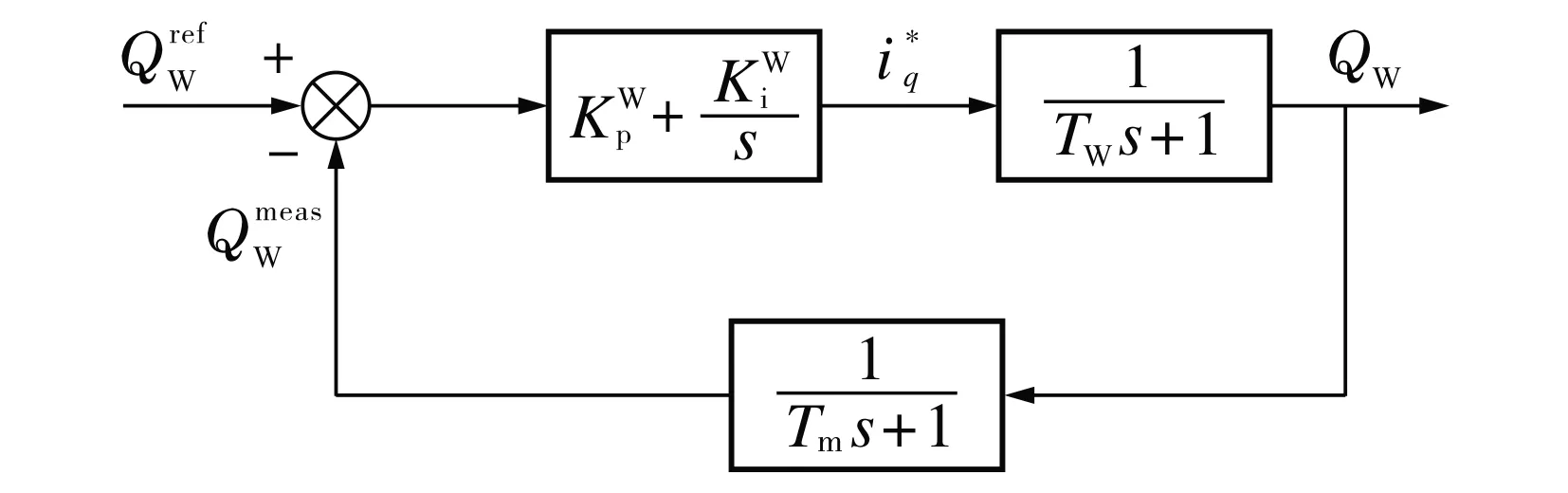
图1 风机的无功功率控制示意图Fig.1 Block diagram of the reactive power control loop
风机的无功功率控制可表示为
(1)
(2)
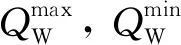
1.2 静止无功补偿器
SVC的控制模式可分为恒定电压控制和恒定无功控制.采用恒定无功控制模式可以更容易且直接地实现与风电机组的协调,但当控制的电压越限后SVC不能及时提供动态无功来调节被控母线的电压.为了降低控制的复杂度,本文采用恒定电压控制模式.
SVC无功功率参考值可表示为
(3)

VS与无功设备发出的无功功率有关[15-16],本文主要研究风机与SVC间的无功功率协调控制,故无功设备是指风机和SVC,它们之间的关系可表示为
(4)
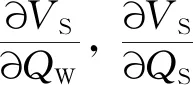
SVC无功控制回路的动态响应可描述为
(5)
(6)
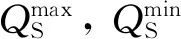
1.3 通用数学模型
本文侧重研究风电场内快慢无功设备的协调控制算法,故不考虑风电场中风机之间的无功出力和风力机间无功出力的分配.假设所有风机为同类型的风电机组且参数设置一致,将风电场等效为一台风机,对等效风机和SVC建立统一的数学模型.在此研究背景下,并网点的电压VPCC主要受风机和SVC的影响,于是有
(7)
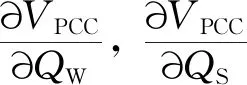

(8)
综上所述,以并网点电压为控制目标、风机和SVC为无功补偿装置的风电场无功电压协调控制结构如图2所示.
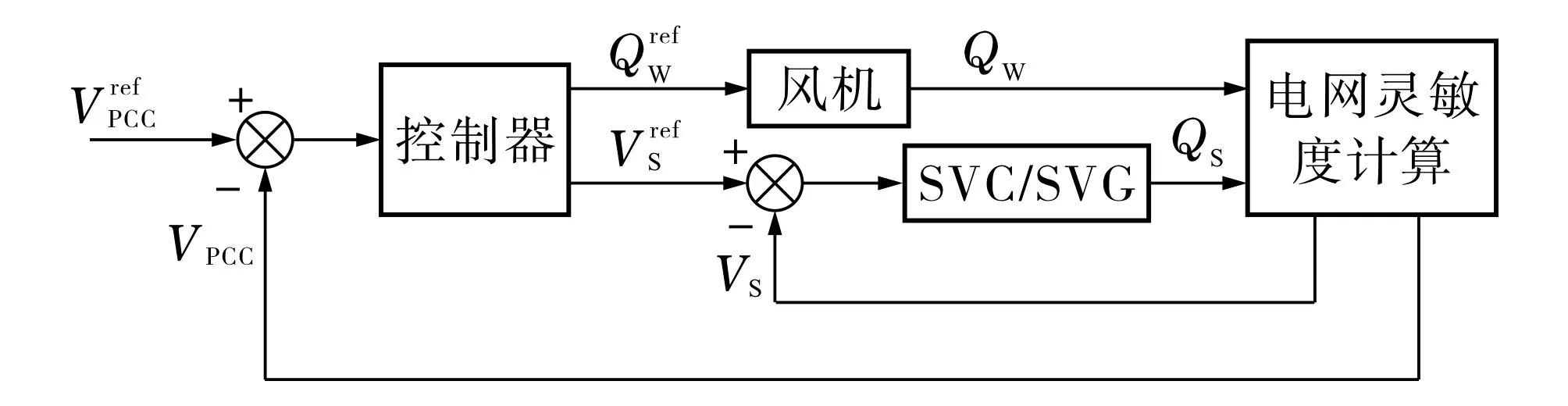
图2 风电场的电压控制结构示意图Fig.2 Block diagram of the voltage control of wind farm
2 控制设计
2.1 扰动观测器
为了方便表示控制系统所受扰动情况,系统的五阶数学模型可表示为
(9)

(10)
干扰观测器能通过对象的输入输出及名义模型信息对干扰进行估计并有效抑制扰动.设计基于状态空间方程(10)的干扰观测器为
(11)
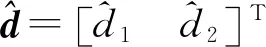
(12)
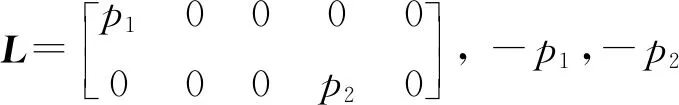
为满足实际应用需求,当系统的采样周期T很小时,采用前向差分离散化方法可获得式(11)的离散形式:
(13)
基于DOB的风电场无功调压系统MPC控制的结构如图3所示.
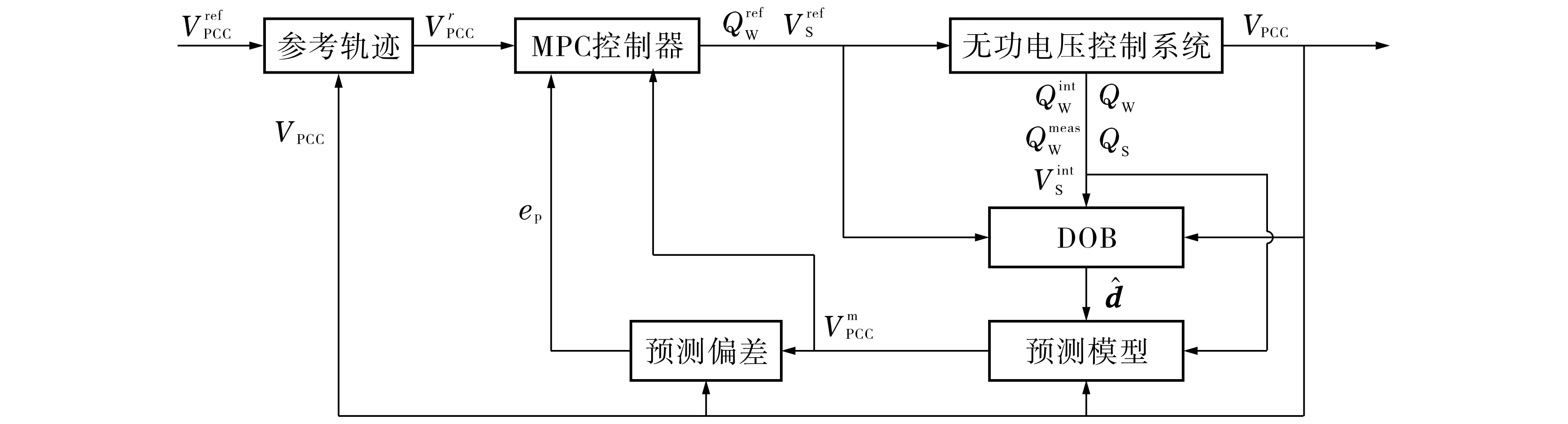
图3 基于DOB的无功调压MPC控制结构示意图Fig.3 Block diagram of MPC for reactive power compensation and voltage control based on DOB
2.2 MPC控制器
(14)
其中输出变量y(k)=VPCC(k).由于目标函数中须对SVC的无功储备进行控制,为了方便推导,这里将SVC的无功QS也输入其模型,得到离散化的预测模型
(15)
定义当前时刻为k,预测时域为Np,控制时域为Nc,且Nc≤Np.为了方便预测未来输出以及减小算法实现时的计算复杂度,假设:1)预测时域内,控制步长Nc以后的控制量保持不变;2)预测时域内,近似认为扰动是一个常值,即
(16)
根据上述假设,在预测时域Np内,基于扰动补偿的每一步预测输出为:
①k+1时刻:
(17)
其中xm为状态变量x的模型预测值,ym为输出变量y的模型预测值;
②k+2时刻:
(18)
③k+Np时刻:
(19)
定义基于扰动补偿的控制输入序列U、预测输出序列Ym及无功功率序列QS为:
(20)
其中U∈RNc×2,Ym∈RNp,QS∈RNp.
根据式(20),将模型预测输出和SVC无功功率整理为向量形式:
(21)

定义预测偏差
ep(k)=y(k)-ym(k).
(22)
由于未来时域内的实际电压值在当前时刻是未知的,所以假设未来时域内的预测偏差与当前时刻相同,即ep(k+Np)=…=ep(k+1)=ep(k),故在预测时域内模型的预测偏差向量为
(23)
系统电压的参考轨迹向量为
(24)
SVC无功储备的参考轨迹为
(25)
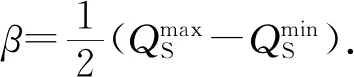
MPC的控制序列可通过优化相关性能指标函数得到,最为常用的是二次型函数.本文目标函数因考虑到实际工况下既须保证并网点电压的偏差不能过大,又需要SVC有足够的无功储备量,故定义性能指标函数为
J=(Yr-Ym-Ep)TQ(Yr-Ym-Ep)+(QS-QSr)TR(QS-QSr),
(26)
其中Q,R分别为系统输出值和无功功率的加权系数矩阵.为了简便,加权矩阵可选取对角矩阵形式:
Q=diag(q1,q2,…,qNp),R=diag(r1,r2,…,rNp).
(27)
将预测输出方程(21)代入性能指标函数(26),可得
(28)
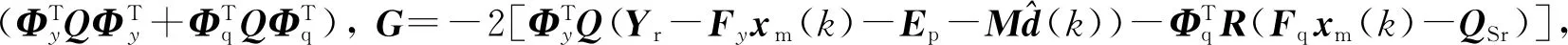
(29)
由极值必要条件∂J/∂U=0可得控制序列
(30)
将所得控制序列U*的第一个元素作为控制对象的实时控制输入,则当前时刻风机和SVC/SVG的控制输入为
(31)
3 仿真分析
为了验证本文算法的有效性,现通过测试本文算法和MPC控制算法下的电压响应曲线及抗干扰能力进行对比分析.设置MPC算法参数:参考轨迹α=0.85,加权系数比q:r=500,预测步长NP=30,控制步长Nc=1(即认为在预测时域内控制量保持不变).在t=0.2 s时加d1=10+3e-t的无功扰动,在t=0.3 s时加d2=-10的无功常值扰动.该仿真条件下的电压响应曲线如图4所示.
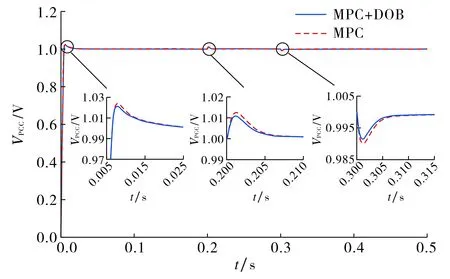
图4 不同控制算法下的电压响应曲线Fig.4 Voltage response curves under the different controllers
由图4可知,相比于MPC控制,基于DOB的MPC能较好地跟踪给定值且更快地抑制扰动.当控制器参数保持一致时,2种控制方法的上升时间基本相同,但基于DOB的MPC由于加入了扰动估计值的前馈补偿,能够较快地抑制扰动,故本文所设计的基于DOB的MPC控制方法具有更强的抗扰动性能.
4 结语
本文针对风电场电压支持和无功补偿问题,提出了一种基于模型预测的多时间尺度电压协调控制策略.该方法可以协调风电场内具有不同时间常数的无功补偿设备,并且为抑制系统可能受到的扰动设计了扰动观测器.仿真结果表明,本文所提方法能够提前响应系统可预测变化,及时追踪电网电压波动,有效提高电压控制水平,并且扰动观测器的设计可使得系统在受到扰动时电压能快速恢复到给定值.
