基于T-S故障树的城市综合管廊内燃气管道可靠性分析

沈颖

（江苏城乡建设职业学院公用事业学院，常州 213016）

一、引言

城市地下综合管廊就是一个用于集中敷设电力、通信、广播电视、给水、排水、热力、燃气等市政管线的公共隧道。城市综合管廊的应用大大避免了各种管线各自为阵，对路面反复开挖的现状[1,2]。

大部分管线进入城市综合管廊的技术已成熟，但是燃气管道是否入廊至今仍存在争议，因为存在一定的风险[3,4]。城市综合管廊为地下构筑物，通风条件较差，一旦发生燃气泄漏，火焰传播速度快，燃烧和爆炸的风险较大。由于城市综合管廊中集成了很多其他管线，一旦发生燃烧或爆炸会对其他行业造成影响，形成次生灾害。因而天然气管道安全及入廊后的安全运行管理是国内外专家学者和天然气企业关注的重点。多个研究团队利用利用肯特法对城市综合管廊的安全风险进行分类辨识，研究了影响因素，厘清综合管廊安全事故的基本事件及特点，形成管廊事故辨识体系，构建了城市综合管廊事故树基本模型[5,6]。

本文以故障模式为底事件建造城市综合管廊内燃气管道泄漏T-S故障树。针对实际系统故障数据缺乏、故障机理复杂多样等原因导致的T-S故障树底事件失效可能性的不确定性问题，将区间模型引入T-S故障树分析，解决底事件失效可能性不易精确获取的问题；进而对系统进行可靠性分析，求得廊内燃气管道泄漏故障树顶事件的故障概率、各底事件的概率重要度和关键重要度，为廊内燃气管道维护和故障发现提供依据。

二、燃气管道T-S故障树

对于城市综合管廊内燃气管道而言，最为严重的故障主要是管道泄漏失效，结合管道现场特点，导致其产生的原因主要可以归结于外腐蚀、管道缺陷、自然灾害、应力腐蚀开裂、压管严重以及误操作等几个方面。廊内燃气管道一旦发生泄漏故障，危害极大，直接影响管道内气体的正常运输以及管廊周围的安全。以管道泄漏失效作为顶事件建造了T-S故障树，如图1所示。

图1 综合管廊内燃气管道T-S故障树

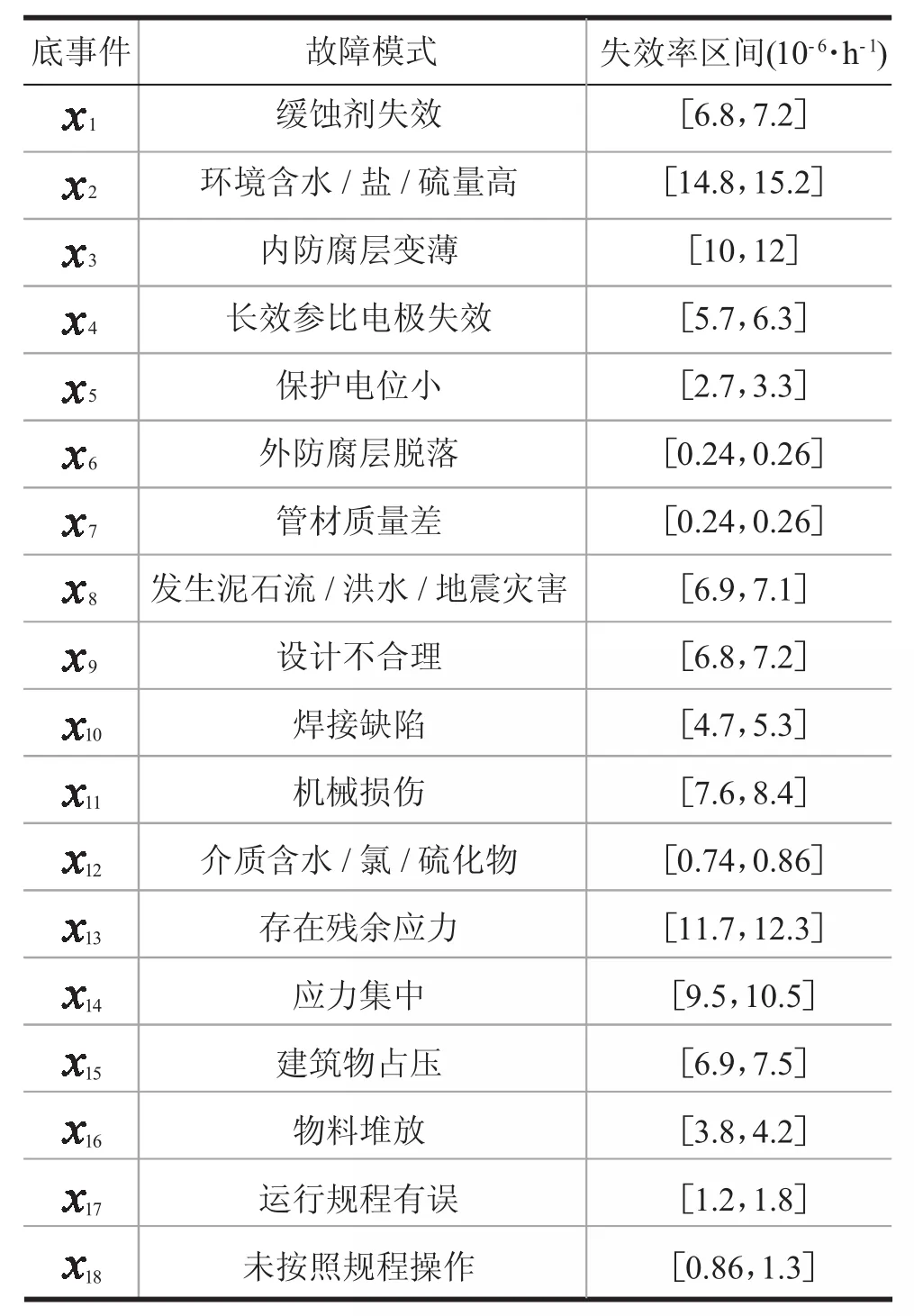
表1 底事件及其失效率区间

三、可靠性分析

根据所建造的T-S故障树，将区间模型引入T-S故障树分析，对城市综合管廊内燃气管道进行可靠性分析，求得廊内燃气管道泄漏的故障概率区间、各底事件的概率重要度区间和关键重要度区间。

（一）故障概率求解

在区间模型中，不确定性变量用一个具有上、下界的区间集合来定义[7,8]。区间变量X表示为：

式中X∈R为实数集R中的有界闭区间变量；X(L)为区间变量的下界；X(U)为区间变量的上界，X(L)，X(U)∈R，且X(L)≤X(U)。当区间数的上下界相等时，即X(L)=X(U)，区间数则变为一个数值。

假设有两个区间变量X1，X2，且X1=［X1(L)，X1(U)］，X2=［X2(L)，X2(U)］，则X1，X2组成一个二维的箱体模型，如图2所示。

图2 二维箱体模型

区间的上下界是用一对实数表示的，使得它具有算术运算的性质，且区间运算仍然是闭的[9]。因此，以下运算规则在区间模型中成立

城市综合管廊内燃气管道平均每年的实际工作时间为t=7200h，若各底事件的寿命均服从指数分布，则底事件xi的可靠度与故障概率可由式(6)和式(7)求得

将区间模型引入T-S故障树分析[10,11]，底事件的可靠度与故障概率可用式(8)和式(9)表示。

假设T-S门的输入事件总数为n，逻辑规则总数为r，输出事件为y，T-S门输出事件的故障概率可用式(10)表示。式中T-S规则l（l=1，2，…，r）的执行可能性F0l可以由式(11)计算得到

根据所建T-S故障树以及给出的基础数据，进行编程并计算，求得中间事件的故障概率区间，如表2所示。

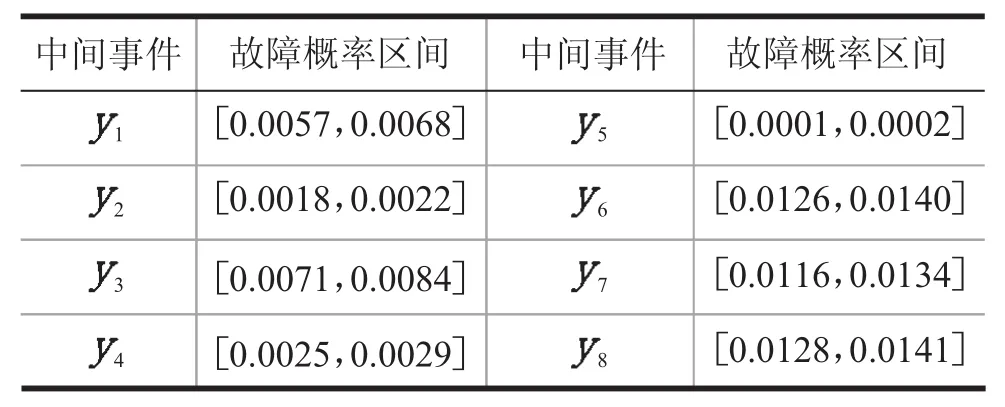
表2 中间事件故障概率区间

进而求得系统故障概率区间:

传统故障树求解顶事件故障概率需要求得系统顶事件故障的最小割集，最小割集为:{x1}、{x2}、{x3}、{x4}、{x5}、{x6}、{x7}、{x8，x10}、{x9，x10}、{x11}、{x12}、{x13}、{x14}、{x15}、{x16}、{x17}、{x18}。根据容斥定理求得系统故障概率区间Fs(t)为

结果与T-S故障树相同，验证了所提方法的可行性，而T-S故障树无需求最小割集且计算更简便。

（二）重要度分析

重要度分析是故障树分析中的重要组成部分，不同的底事件在系统中呈现非均等的重要性，底事件重要度不仅应用于系统可靠性分析，而且在系统设计优化、系统维护、故障诊断方案提出等方面有着重要的作用。因此用重要度来衡量廊内燃气管道泄漏故障各底事件的重要性对系统可靠性分析具有重要意义。

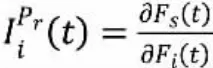
若顶事件的故障概率函数Fs(t)因系统较为复杂而难以确定，底事件xi的概率重要度可以利用式(13)计算[12]

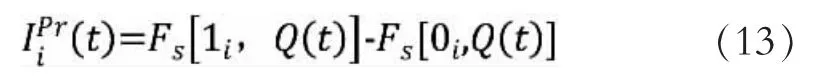
式中，Fs[1i，Q(t)]为底事件xi故障条件下顶事件的故障概率;Fs［0i，Q(t)］为底事件xi正常条件下顶事件的故障概率；Q(t)表示除xi外的其他底事件的组合。

关键重要度表示任意一个底事件Xi故障概率的变化率引起顶事件故障概率的变化率，可定义为

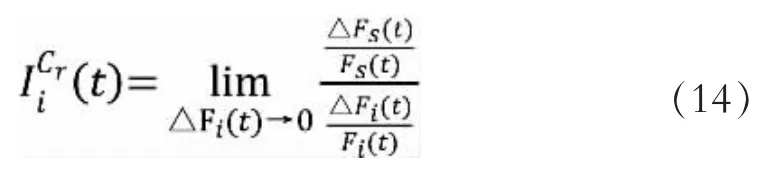
对式（14）进行简化可以得到

概率重要度能反映底事件的重要性，并为系统故障诊断中底事件的重要性计算提供了一种理论依据。关键重要度的意义在于通过改进系统最薄弱的环节以提高系统的可靠性。与概率重要度相比，关键重要度含有部件的概率重要度和其本身的故障概率两个方面。关键重要度不仅体现了部件在故障树中的地位，而且还体现了部件本身的故障概率，能更客观地体现部件对系统故障的影响。

根据式(13)、式(15)，结合区间模型，求得各底事件的概率重要度区间、关键重要度区间如表3所示。

重要度数据可以直观反映出在廊内燃气管道可靠性中重要度较大的因素为内防腐层变薄、机械损伤、存在残余应力和应力集中由(见表3)，因此应重点对这几个方面进行检查和定期维护，同时对这些因素进行有针对性的优化改进可以大幅度降低廊内燃气管道泄漏故障概率，从而改善系统的可靠性。

表3 底事件重要度区间

四、结语

将区间模型引入T-S故障树分析，能够解决了底事件失效可能性的不确定性问题，可以改善实际工程中故障数据不易精确获取的问题；通过分析城市综合管廊内燃气管道泄漏故障因素，对其进行建树分析，求得系统的故障概率区间和各底事件的概率重要度区间、关键重要度区间，为发现系统的薄弱环节、缩短故障查找与维修时间以及系统的优化改进提供了依据。