结合半监督AP聚类和改进相似度的推荐算法

李昆仑，赵佳耀，王萌萌，于志波

(河北大学 电子信息工程学院，河北 保定 071002)

1 引 言

推荐算法可以分为基于内容的推荐、基于协同过滤的推荐、基于关联规则的推荐、基于知识的推荐等类别，其中协同过滤推荐是应用最广泛的推荐算法之一，但它也存在数据稀疏性、冷启动问题、可扩展性等问题[1].目前针对稀疏性问题的优化可以分为两大类，第一类是通过聚类或引入优化因子的方式提高相似性度量精度；第二类是按照某种方法对部分缺失值进行填充[2].本文采用第一类优化方法，以提高相似性度量精度.

一方面，由于传统的大多数聚类算法的聚类精度难以满足要求，因而可以从聚类方式的角度进行改进.H.Koohi等人使用Fuzzy C-Means聚类对用户分组，精确了最近邻用户搜索范围，解决了近邻用户寻找不准确问题[3]；为了解决H.Koohi的算法中用户聚类结果不理想问题，S.Fremal等人根据属性进行项目聚类，在多个集群中对目标项目进行评分预测，然后使用加权策略将这些预测评分合并[4].为了进一步提高协同过滤算法中聚类模型的性能，以提升推荐质量和推荐效率，本文提出了一种基于k近邻密度估计的半监督AP聚类(Semi-supervised AP clustering based onk-nearest neighbor density estimation，SAP-KND)：使用基于近邻密度选择的成对约束信息与上层推举思想改进AP聚类.另一方面，也可以考虑从相似性度量的角度进行改进.M.Shamr等人考虑到并非所有评分对用户都有相同的重要性，将评分权重融入到Pearson相关系数中[5]；S.Bag为了将用户的总评价向量融入相似度计算，将相关Jaccard相似度和均方距离相似度进行了融合[6]；孙红等人在Pearson相似度原理上添加物品热门因子，一定程度上提高了推荐的精确度[7].

根据上述分析，本文提出了一种基于半监督AP聚类和改进用户相似度的协同过滤算法：首先使用基于近邻密度选择的成对约束信息与上层推举思想改进的AP聚类(SAP-KND)得到项目类簇；然后利用初始评分矩阵构造用户对项目类簇的偏好矩阵；最后使用改进后的用户相似性度量得到近邻用户集，通过具有相似偏好的用户评分预测评分值.本文实验部分使用vowel、glass 及Movielens这3种数据集，采用FMI值和平均绝对误差(MAE)评价本文算法，并得到实验结果.

2 相关工作

由上文可知，传统协同过滤算法中相似性度量对象较为单一，无法同时利用项目侧和用户侧的近邻项信息.近年来为了解决此问题，研究人员提出了一种基于项目类别偏好的混合协同过滤算法(Hybrid Collaborative filtering algorithm based on user preference model，UP-HCF)：K.Shinde等人对稳定的项目特征进行聚类，构建用户对项目类别的偏好模型，并结合传统协同过滤算法预测评分，寻找近邻用户得到推荐结果[8]；J.Li等人根据电影属性形成电影特征向量，并结合用户评价矩阵生成用户兴趣向量，通过迭代的方式对电影特征向量和用户兴趣向量进行相互更新，然后根据用户兴趣向量构造用户相似度矩阵[9].

在传统的UP-HCF算法中使用的K-Means、K-medoids、DBSCAN、BIRCH等无监督聚类算法在面对噪音数据和大规模数据时，存在一定的局限性，进而导致聚类算法无法在稀疏的数据集中完成推荐任务.近邻传播聚类(Affinity Propagation，AP)与以往的无监督聚类方法相比，此方法可以更快的处理大规模数据，不受限于选择初始类代表点的选择，且能够得到高精度聚类结果，其最大的优点在于，AP算法的输入矩阵没有规定相似度矩阵的对称性，因此提高了AP算法的泛化能力[10].AP算法假设所有的样本点都为聚类中心；在各个节点(样本点)之间，存在被称为吸引度(Responsibility)和归属度(Availability)的两种消息在不断地进行迭代传递；直到找到距离最近的类代表点的相似度之和最大的数据点，作为最优的类代表点集合[10].

现有的半监督聚类算法大致可分为两类：基于约束的半监督聚类、基于距离的半监督聚类.其中基于约束的(constraint-based)半监督聚类：在聚类过程中遵循约束条件，使聚类结果满足所有约束信息，must-link约束表示两个样本必须被聚到同一类簇中，cannot-link约束表示两个样本必须被聚到不同类簇中[11].由于成对约束具有弱监督特性，在实际问题中往往更容易获取先验信息.但是，对于复杂结构的数据集，AP聚类通常不能得到合理的聚类结果.AP聚类的相似度矩阵S包含数据对之间的信息，因此，利用先验信息约束数据对，更容易达到提高聚类精度的目的.基于以上启发，本文考虑将半监督AP聚类算法应用到推荐系统，旨在进一步提高推荐性能.

传统UP-HCF算法的相似性度量方式仍然存在以下问题：1)计算用户相似度时往往只依赖评分数值的大小；2)将所有用户或物品对计算相似度的贡献视为一致的；3)没有考虑到用户评分行为的相似性带来的影响.为了全面客观地评价用户相似度，本文使用用户活跃度和用户行为轨迹对相似度进行改进.

3 基于k近邻密度估计的半监督AP聚类

利用先验信息改进相似度矩阵，可以有效优化AP算法.但是在实际问题中，数据本身没有任何先验信息；无论是球型数据结构还是流形结构，同一类簇的样本主要分布于一个密度较高的区域，类簇之间通常存在于一个低密度区域，且簇中心只是部分存在于高密度区域.为了避免Parzen算法中窗函数h的选择问题，本文采用了k近邻思想估计局部密度，然后假设处于高密度极值点的样本的k个最近邻样本必定与该样本属于同一类别，并且在极为稀疏的几个区域的大部分样本存在cannot-link关系.基于此极端假设对数据集进行少量标记，可以使靠近的点更近，远离的点更远，同时避免must-link约束信息过于集中而产生违反问题.

虽然针对较复杂的数据倾向于产生更多的类，说明算法具有较高的聚类精度，但是往往无法满足实际需求，无法得到合理的聚类结果.为了避免增加算法复杂度同时可以保障理想的聚类结果，首先使用传统欧式距离计算相似度矩阵，然后使用马氏距离处理AP聚类结果.因此SAP-KND使用马氏距离(Mahalanobis distance)并融合上层推举思想，得到期望的簇数.SAP-KND算法详细过程如下.

k近邻密度估计法不断扩大体积Vi直到区域内包含k个样本点，进而对数据集进行密度结构分析.则样本xi的局部密度估计值如式(1)[12]：

(1)

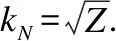
(xi，xj)∈must-link&&(xj，xk)∈must-link⟹(xi，xk)∈must-link

(xi，xj)∈must-link&&(xj，xk)∈cannot-link⟹(xi，xk)∈cannot-link

利用上述传递关系可以进一步扩大M集和C集.

本文采用欧式距离构建相似度矩阵S[s(i，j) ]Z×Z，使用成对约束信息可将数据集分为3种集合，这里的集合M又称为高密度集，设置集合D{D∈X&D∉M∪C}为中密度集，集合C又称稀疏集.按如下方法调整相似度矩阵：

s(k，k)为偏向参数(Preference)，AP算法假设所有点成为簇中心的可能性相同，即s(k，k)=p，一般将p值设置为相似度矩阵的均值p=median(s)，且p越大簇数越大.在SAP-KND算法中，需要对AP聚类结果进行再聚类，所以这里将p值设置稍大.

吸引度r(i，j)代表点j适合作为i的类代表点的代表程度；归属度a(i，j)代表点i选择点j作为其类代表的适合程度.利用相似度矩阵S和归属度矩阵A=[a(i，k)]，更新吸引度矩阵R=[r(i，k)]：

r(i,k)←s(i,k)-max{a(i,k′)+s(i,k′)},i≠k

(2)

r(k,k)←p(k)-max{a(k,k′)+s(k,k′)},i=k

(3)

再根据吸引度矩阵R更新归属度矩阵A：

(4)

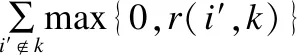
(5)

引入阻尼因子λ，默认值为0.5消除可能出现的震荡：

rnew(i,k)=λ×rold(i,k)+(1-λ)×r(i,k)

(6)

anew(i,k)=λ×aold(i,k)+(1-λ)×a(i,k)

(7)

假设第t次迭代后簇中心集合为Etold，如果Et=Et-1，则稳定次数δ加1，若此时δ=stableNum则完成迭代，最后计算A+R的值得到AP过程的簇中心点：

(8)

由于AP算法容易产生较多的类，无法满足本文推荐模型的聚类目标，所以需要对簇中心进行再聚类，使聚类算法输出一个固定的类簇数m.这里考虑融入上层推举思想：计算簇中心点间的距离，选出距离最近的一对簇中心，将所代表的类簇合并，并计算新类簇的簇中心；重新计算新簇中心和其他簇中心的距离，重复上述过程直至得到期望类簇数目m和最终簇中心集合Etnew.鉴于推荐算法所使用的数据集中各类别的占比具有很大的差异性且簇中心具有较强的代表性，所以此过程要考虑到簇中心各分量的差别以及样本各特征之间的联系，因此这里使用马氏距离度量簇中心间的相似性：

(9)

其中Σ-1为矩阵[ci，cj]的协方差矩阵的逆矩阵[14].

本文聚类算法步骤如算法1所示.

算法1.基于k近邻密度估计的半监督AP聚类算法

输入：数据集X，kN，p，δ，stableNum，m.

输出：簇中心集合为Etnew，m个类簇.

Step1.使用k近邻密度估计法得到p1，…，pZ，使用kd-tree选择出集合H、集合L;

Step2.分别将集合H和集合L通过特定方式标记为must-link和cannot-link，生成M约束集和C约束集；

Step3.使用成对约束对相似度矩阵进行3段式处理，并进行AP聚类；

Step4.不断交替更新矩阵A和矩阵R，迭代完成得到Etold；

Step5.利用上层推举思想进行再聚类，簇中心间距离使用马氏距离，得到Etnew，m个类簇.

4 改进用户相似性度量

针对传统用户相似度存在的问题.

问题1.假设A用户与B用户只有两个共同评分项目且分值大小相近，而A用户与C用户拥有30个共同评分项但是A的评分均值大于C，则得到的相似度结果就是：AB之间的相似程度远远大于AC之间的相似度.而事实却恰恰相反，这就造成了极大的误差.

问题2.如果一个爱好广泛的用户对所有的类型都有评分记录，那么这个用户就没有其利用的价值，共同评分项的数量也不能完全成为决定相似度的因素.为了全面客观地评价用户相似度，本节基于Jaccard相似度(轨迹相似度)[6]的思想和皮尔逊相关系数法(Pearson)[15]改进用户相似度.两种传统相似度公式分别如式(10)、(11)所示：

(10)

(11)

4.1 活跃用户惩罚因子与轨迹相似度

在稀疏矩阵中，用户间评论项目的轨迹信息对降低推荐所产生的误差尤为重要.针对问题一可以考虑结合Jaccard相似度，但是Jaccard相似度只考虑了用户间共同评分项的数量，没有利用共同评分项的评分等级.Tanimoto系数(广义Jaccard相似度)的元素的取值可以是实数，所以也同时将评分等级的影响融入了计算结果，因此本文使用了Tanimoto系数，计算方式如式(12)：

Ej(A,B)=(A*B)/(‖A‖2+‖B‖2-A*B)

(12)

其中，其中A、B分别表示为两个向量，向量中每个元素表示为向量中的一个维度，在每个维度上，取值为非二值性的，A*B表示向量乘积，‖A‖2表示向量的模.

针对问题二本文加入了活跃用户惩罚因子.本文的活跃用户惩罚因子根据用户对19类电影类型的评分记录的数量来衡量.根据函数的特性，本文使用y=1/ln(2x-1)(ln─以e为底的对数)作为惩罚函数，N(u)代表活跃用户u的活跃度，当活跃度到达阈值β时，则启动惩罚因子，表达式如(13)：

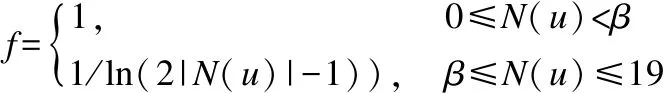
(13)

4.2 本文用户相似性度量

在计算相似度时，本文综合考虑了活跃用户惩罚因子f、轨迹相似度E以及实际评分对结果的影响，将活跃用户惩罚因子融入Pearson相似度并于轨迹相似度相结合，旨在为相似性度量提供更多的信息，缓解数据稀疏性带来的影响.与传统Pearson相似度不同的是，式(14)中的i表示用户x和y的共同评分项目类别，并且融入了惩罚因子f.本文相似性度量具体公式见式(14)：

(14)

(15)

newSim=∂Sim1(u,v)+(1-∂)Sim2(u′,v′)

(16)

其中，Sim2(x，y)为Tanimoto系数，x′、y′代表经过数据处理的用户评分向量；N(u)代表活跃用户u的活跃度，这里的活跃度是指用户对19个种类的评价状况；∂为权重因子，取值范围是[0，1].

5 基于半监督AP聚类和改进用户相似度的协同过滤算法

对于本文算法有以下两点论述：1)相似性度量依据具有相似偏好的用户生成相似度矩阵，所以本文算法相似性度量结果的有效性极大依赖于用户对电影类别的偏好；2)一个电影标签可能同时存在于多个电影中，每个电影还有多个特征向量，因此数据集的复杂结构增加了聚类的难度.使用近邻密度寻找成对约束的方法可以初步标记各个类别的初始位置和分类间隔的位置，最后使用SAP-KND算法可以得到一个更加精确的电影分类结果，进而可以更准确的得出用户对电影类别的偏好.具体实现过如算法2所示.

算法2. 本文算法

输入：评分矩阵R，近邻个数N.

输出：预测评分矩阵R*，MAE值.

Step1.加载数据集，得到评分矩阵R和电影特证矩阵M.

Step2.使用SAP-KND对电影特征矩阵M进行聚类，将全部电影分为19类(电影的全部类别).

Step3.聚类结果结合评分矩阵R，得到每个用户对19个电影种类的平均分，生成矩阵U1，且U1中还有大量缺失值.

Step4.使用本文提出的相似度newSim(x，y)，基于U1构造用户相似矩阵U2.

Step5.根据用户相似矩阵U2生成近邻用户集(top-n)，使用式(17)对U1进行缺失值填充，得到矩阵U3.

Step6.观察缺失值所属电影种类，根据U3将评分矩阵R中的缺失值填充，生成新的评分矩阵R*.

Step7.加载测试集数据，使用评分矩阵R*计算MAE.

其中，评分预测公式见式(17)：

(17)

6 实验与分析

6.1 实验环境及数据集介绍

本实验在CPU为 Intel(R) Core(TM)i5-7200U，运行内存为4GB内存的计算机上运行，使用python3.6中的sklearn等程序包进行实验.本文的推荐算法实验数据集采用的是Minnesota大学Grouplens项目组制作的Movielens100k版本的数据集[3].训练集和测试集分别使用ua.base文件和ua.text文件.

本文采用的聚类实验数据是从 UCI 机器学习数据库中选出2个标准数据集：vowel和glass.采用5重交叉验证(cross validation)，每次从原始数据集中抽取80%作为训练数据集，剩余的20%作为测试数据集.相关信息见表1所示.

表1 数据集相关信息Table 1 Data set

6.2 评价指标

本文所采用的聚类评价指标是FMI指标，其将准确率和召回率结合在一起来评价聚类结果.对于实际类别w和簇类Cm的准确率和召回率分别是：pre(w，Cm)=Nwm/Nm，Rec(w，Cm)=Nwm/Nw其中：Nwm代表簇类m中实际类别为w的样本数；Nm代表簇类m中的样本数；Nw代表实际类别w中的样本数[16].对于整划分的FMI值为：

(18)

其中FMI的取值越大则算法越准确.本文所采用的推荐质量度量标准是平均绝对误差MAE (Mean Absolute Error)，表达式如式(19)所示：

(19)

其中pi表示系统对用户的预测评分，qi表示用户实际的评分.

6.3 实验结果及分析

6.3.1 聚类算法分析

6.3.1.1 不同密度估计参数kN值对t、MAE的影响

首先，针对SAP-KND中簇中心的迭代次数t设置对比试验，以体现算法在不同kN值下的收敛速度.其次，为了得到算法在不同kN值下的预测准确度，这里设置了针对MAE值的对比试验.控制其他参数不变的情况下，将kN设置为24，28，32，36，40，44，48，依据7个数值进行实验从而获取迭代次数t和MAE值，依据这两个变量可以更好的确定最佳kN值.在寻找最近kN值的同时，将传统AP算法的迭代次数t和F值与SAP-KND算法进行对比.

图1 不同kN值对迭代次数t的影响Fig.1 Influence of different kN values on iteration times t图2 不同kN值对MAE的影响Fig.2 Influence of different kN values on MAE

针对SAP-KND算法的曲线.考虑到实验中的偶然性因素，每组均通过多次实验取平均值的方式得到上述结果.结果显示，图1中可以清晰的得到折线图总体呈现一种低凹形状，因此kN范围在[28，40]区间时的迭代次数t较少，意味着迭代次数较快达到了稳定次数stableNum；图2中显示折线图总体趋势与图1表现相类似，但也有细微差别，可以得到在本文算法中迭代次数的大小对MAE值具有相对较大的影响而且呈正相关.因此，当kN取28与32时推荐精度相对较高，综合观察两组实验可以得到SAP-KND算法在kN的取值在32附近时算法综合性能最好.

针对AP算法的曲线.图1的实验结果表明，成对约束的引入使数据集得到了稀疏化，进而降低数据复杂度，使得算法较快满足类簇中心集{ci}的稳定条件.两组实验表明SAP-KND算法提高了聚类精度，加快了收敛速度.

6.3.1.2 不同聚类算法在不同数据集下的对比

为了更好的体现本文聚类算法的优越性.在其他参数不变的情况下，SAP-KND算法针对3个数据集设置不同的m值，在最佳kN值的情况下计算FMI值.其他两种算法取10次5重交叉验证的最优值作为FMI值，并设计以下对比实验，见表2所示.

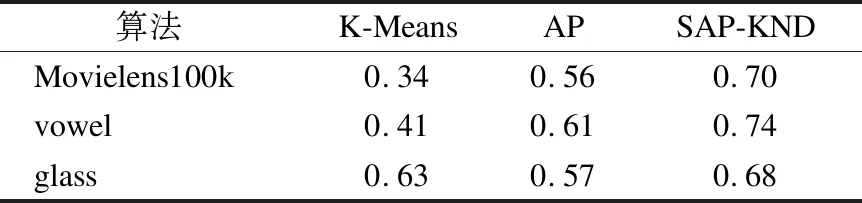
表2 不同算法在数据集下的FMI值Table 2 FMI values of different algorithms in data sets

表2的实验结果得到了以下结论：1) SAP-KND算法相较于传统AP算法得到了一定的提高，相较于K-Means具有明显的优势；2) K-Means算法适合处理小规模复杂度较低的数据；3) 观察AP算法及其改进算法SAP-KND，AP系列算法适用于不同规模的数据，其稳定性较高；4) 对比两种AP算法，验证了近邻密度标记规则的有效性，使不同类簇的样本点更好的分割开来.

6.3.2 本文算法在不同相似度参数下的对比

活跃因子与活跃程度的函数关系如图3所示，纵坐标是活跃因子f，横坐标是活跃度N(u).在计算相似度时，由于f作为相似度公式分子的一部分并作为一种限制因素，所以其取值不能大于1.原始图像纵坐标的取值范围(0，+∞)不能应用于实际的算法计算，因此本文规定取值范围为0

本节旨在直观的表现出不同活跃度阈值β在不同权值∂下的MAE值的变化情况，同时得到MAE到达最小值时两参数的最佳取值.∂值的意义可以描述为：计算相似度时更偏重用户可靠度(行为轨迹因素)或者更偏重分值的差异因素.当近邻个数设置为12时，将β初始值设为6，以1为间隔逐步增至16；权值∂选取0.2、0.4、0.6、0.8，实验结果如图4所示.

图3 f的函数图像Fig.3 Function image of f图4 不同相似度参数下的对比Fig.4 Comparison of different similarity parameters

首先，观察MAE值的变化情况可以得出，β值对预测精度的影响大于∂值产生的影响.当∂=0.4时节点处在最低处，所以此处为最优权值，进而说明用户的轨迹相似性对相似度的准确性影响更大.其次从总体的折线走势中可以看出，4条曲线总体走势基本相似，说明β值对预测精度的相对影响不随着其他因素的变化而变化.最后，观察β在6至12的区间时变化缓慢，在β为14时到达了最低点，随后β为16时出现了一个大幅度增加.结果说明当用户的活跃度为14时启动活跃因子为最佳时间，如果对活跃度过于敏感会得到适得其反的效果.

6.3.3 本文相似度有效性验证

为了验证本文相似度的有效性，将没有考虑融入用户活跃度的算法( algorithm1)、没有考虑轨迹相似度的算法( algorithm 2)、只考虑轨迹相似度的算法( algorithm3)作为3种对比算法，与本文算法(The new algorithm)在不同近邻个数N的情况下进行对比.选取的目标用户最近邻居数初始化为4，并以2为间隔逐步增至20.

从图5中首先可以看出，algorithm3的MAE值明显高于其它3个算法，并与algorithm2相比较可以得出：只考虑用户之间的评分轨迹相似性而不考虑评分的数值最终会导致相似度的有效性极低，并且Pearson相似度的有效性要高于Tanimoto系数；其次观察到 algorithm2随着近邻数的增加，MAE值下降的趋势较为明显，这说明：近邻用户越多，活跃用户因子f的惩罚功能对算法精度的影响越明显.最后综合观察4种相似度所对应的4条曲线可以得出：综合考虑用户的活跃度、可靠度以及用户实际评分3种因素的协同过滤推荐算法有效性明显高于单独考虑一种因素的算法，同时也验证了本文算法的有效性.

图5 4种算法在不同近邻个数N下的对比Fig.5 Comparison of four algorithms under different N neighbors

6.3.4 不同算法在不同近邻个数N下的对比

为了验证本文算法的有效性，这里选择了4种算法作为对比进行实验：

1)基于用户聚类协同过滤算法(Collaborative filtering algorithm based on user clustering，UBCF)[3]；

2)基于项目聚类和加权策略的协同过滤算法(Collaborative filtering algorithm based on item clustering and weighting strategy，ICWSCF)[4]；

3) 基于用户偏好的混合协同过滤算法(Hybrid Collaborative filtering algorithm based on user preference model，UP-HCF)[5]；

4) 融合混合兴趣向量和评级自适应权重的推荐算法(A recommendation algorithm that hybrid interest vectors and rating adaptive weights，IVAWCF)[6].

最近邻居数目的选定对推荐质量有着重要的影响，为了对不同邻域条件下的实验结果进行评价和比较，本节将4种算法与本文算法(The proposed algorithm)在不同近邻个数N下进行对比.将选取的目标用户最近邻居数初始化为4，并以2为间隔逐步增至20，在kN、∂、β为最优值的情况下进行实验，实验结果如图6所示.

图6 不同算法在不同近邻个数N下的对比Fig.6 Comparison of different algorithms under different numbers of neighbors N

结果显示，IVAWCF的MAE值随着近邻数的增加呈下降趋势并逐渐趋于平缓；本文算法与UP-HCF的算法相比曲线走势明显较为平缓且在N为10时MAE值最小，剩余两种算法在N为12时MAE值最小，通过综合观察近邻个数为10-12时推荐效果最佳.

本文算法在近邻个数相同的几种情况下比UBCF 、IVAWCF和IVAWCF在预测精度上具有明显的提高；IVAWCF具有较高的近邻用户需求量，本文算法在低近邻用户需求量时更具有优势.通过与ICWSCF算法的对比可以证明：同时利用用户和项目两侧信息寻找近邻用户的方法明显优于仅凭单一侧寻找近邻项目的方法.与UP-HCF算法相比，本文算法在稳定性上得到了明显的提高，在推荐精度方面也得到了一定提高，说明SAP-KND算法在一定程度上克服了无监督聚类算法的局限性.

7 总 结

传统的基于项目类别偏好的混合协同过滤算法存在相似性度量精度较低的问题，为此本文首先提出一种半监督聚类算法-SAP-KND算法，并用于项目聚类，然后对相似度计算方式进行了改进.理论分析和实验结果均表明：与传统算法相比，本文算法可以保证近邻用户与目标用户具有更高的相似度进而提高了推荐的准确性与稳定性.本文的下一步工作考虑将上述半监督聚类与迁移学习相融合，希望可以利用更丰富的偏好信息为用户推荐项目.