融合SDE算法和双路加权门控循环神经网络的股价走势预测模型

吴 彬,张 勇,唐颖军

(江西财经大学 软件与物联网工程学院，南昌 330013)

1 引 言

数据预测作为数据挖掘的主要研究分支之一,一直以来备受学者们的关注.对金融时间序列进行预测从而挖掘金融市场的运动规律进而准确地预测金融市场的走势，有助于金融投资者制定出低风险、高收益的投资策略，并且有利于金融市场的平稳运行[1].然而，股市这类金融市场是一个复杂的动力学系统，具有非线性、非平稳、易变性以及高噪声的特性，这使得股价这种时间序列数据的预测过程会受到多种复杂因素的影响[2].随着数据的获取途径不断扩大，以及信息提取能力和数据预测技术的不断提升和发展，特别是深度学习等人工智能技术的蓬勃发展，为股价等金融时间序列的预测这一难题开辟了新的研究空间以及提供了更多的解决思路和可能性.

本文基于神经网络构建预测模型的基础架构，融合自适应差分进化(Self-adaptive Differential Evolution,SDE)算法对实验过程中的网络参数进行寻优，以及引入改良的双路加权门控循环单元进行预测，得到一种优化的股价趋势预测模型.为了直观显示预测效果，提高预测模型实用价值，给投资者和金融研究者提供有价值的预测数据，本模型选择对股票价格的走势方向进行预测，展示个股股价及股票指数的变化趋势.大量的仿真实验验证了该优化的预测模型与其他传统模型相比，预测误差有效降低，预测精度明显提升.

2 相关工作

股市指标预测方法主要包括统计分析方法、传统机器学习方法以及基于深度学习的人工神经网络方法等[3].张永东等[4]比较了指数平滑和长期平均等模型对股市波动性预测的效果，Jeffrey等[5]将差分自回归移动平均模型应用于股价的预测，这些统计分析模型在特定情境下预测股票数据可以取得不错的预测效果，但是这类模型很难准确把握股票数据的非线性特征，面对股市这个复杂系统的诸多影响因素和噪声数据，模型的整体预测性能不够优秀.Sibao Fu等[6]利用支持向量机算法预测金融时间序列数据，T.Renugadevi等[7]利用K-means算法预测股市行情，这些传统机器学习算法的特征提取能力不够强，从而使预测精度受限.

随着深度学习的深入发展和广泛应用，基于神经网络的深度学习预测模型大量出现.吴微等[8]利用BP神经网络预测股票涨跌，有一定的预测性能，但是网络结构过于简单，无法考虑过多的复杂股市规律.邓凯等[9]将遗传算法引入BP神经网络，优化网络参数，从而得到优化的BP网络.Shotaro等[10]意识到了简单的BP网络预测性能不佳，利用具有记忆功能的长短期记忆网络(Long Short-Term Memory,LSTM)对股票走势进行预测，该网络的当前神经单元会受到前一时间点的同单元的输出值的影响，这一特点很适合时间序列的预测，有效避免梯度消失与爆炸、长程依赖等神经网络中常见问题.张金磊等[11]以具有比LSTM更少门结构的门控循环单元(Gated Recurrent Unit,GRU)为网络主体进行预测，预测速度更快且效果更佳.李梅等[12]将LSTM与CNN进行结合，使用多层的循环神经网络构建预测模型，并引入注意力机制，虽进一步提高预测精度，但模型复杂度增高以及训练时间增加过多.

通过对已有研究方法的学习和梳理，本文在前人研究的基础上提出了一种融合SDE算法和双路加权GRU神经网络的股价走势预测模型.双路加权GRU网络的神经单元能同时考虑过去时刻和未来时刻的状态，采用加权方式对过去和未来的双向值进行叠加，并且整个网络结构由SDE 算法全局寻优出最合适的网络参数.

3 本文的预测模型

本文的预测模型分为两大部分，SDE对网络参数寻优和网络预测求解.

3.1 SDE优化网络参数

网络预测求解过程中，选择合适的网络结构参数，比如各神经单元之间连接的初始权值和阈值以及网络单元值的权重系数，会提升整个网络的预测精度，避免局部最优值的出现.参数寻优算法可以得到网络结构中初始权值和阈值等参数的优化组合.差分进化(Differential Evolution，DE)算法是一种基于种群遗传进化的启发式搜索算法，具有很强的自适应性和全局寻优能力[13].为了克服基本DE算法早熟和后期搜索迟钝等缺点，本文采用了自适应的DE变异和交叉因子，使用优化的SDE(自适应差分进化)算法对网络初始结构参数寻优.SDE优化本模型网络参数的工作步骤如图1所示.

图1 SDE算法的工作步骤Fig.1 Working steps of SDE algorithm

本文预测模型中SDE算法寻优参数的详细步骤如下：

1)种群初始化与编码.一个染色体即个体就是寻优过程中的一个解，而种群则是一组个体的集合[14].先随机产生若干个个体，构成初始种群规模，再对每个个体使用实数编码法进行编码.为了寻找最优初始权值和阈值等结构参数，每个个体即每个解的构成为网络结构中各所求参数的集合.

2)确定适应度评价函数并计算适应度.我们用适应度作为“适者生存”的评价标准，个体的适应度即适应度函数值越大，则其被选中的可能性就越大[15].因为本模型中每个个体就是一组可能的参数最优解，将其代入网络中进行训练，用其训练的输出结果与期望输出的平均绝对误差的倒数可以作为评价个体好坏的一个指标，则本文的预测模型就选择此指标作为SDE的适应度函数值，具体如式(1)所示：

(1)

式中，yi为第i个样本的期望输出，oi为第i个样本的实际输出，K为样本数.

(2)

(3)

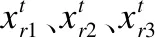
4)交叉.某代进化过程中通过变异产生了一个变异个体，然后将变异个体与每个原个体进行交叉操作以构成候选的下一代新个体，也称实验个体[17].SDE算法的交叉操作通过引入自适应的交叉因子C来完成，自适应交叉因子产生公式如式(4)所示.而交叉操作产生实验个体的公式如式(5)所示.

(4)

(5)

式中，Cmax代表交叉因子的最大值，Cmin代表交叉因子的最小值，t为当前的进化代数，i为个体编号，j为基因编号，rand是介于0和1之间的随机数,jrand是介于1和个体的基因总数之间的随机数.这样的交叉操作公式可以保证每个实验个体至少能获得变异个体中的一个基因.

5)选择.通过一定的方法选择优秀的个体进入后续的变异和交叉过程以及下一次的进化过程[18].通过逐个比较实验个体和原个体的适应度函数值，选择出适应度值更高的个体作为下一代进化的种群新个体.选择操作的公式如式(6)所示：

(6)

通过逐代进化，到达最大进化次数之后，产生的全局最优个体的基因值，就是预测模型网络结构中所需的各最优参数组合.

3.2 网络预测求解

网络预测求解部分主要由网络输入层、网络编码器、网络解码器构成，解码器的输出值即为预测模型的输出.编码器和解码器均基于双路加权GRU单元实现.

3.2.1 网络模型结构

本文提出的预测模型的网络结构以循环神经网络为主体，因为循环神经网络能够接收历史信息，具有记忆功能[19]，很适合处理股票这种复杂的时间序列数据.本模型采用优化的经过加权的双路门控循环单元(Bidirectional Gated Recurrent Unit,BiGRU)作为循环网络的神经单元，充分利用过去和未来数据对股价预测的影响.预测模型的输入数据经由编码器和解码器处理之后，得到分类预测结果.网络模型的整体结构如图2所示.

图2 网络预测模型结构图Fig.2 Network prediction model structure diagram

图中Xt为某一时刻的股票时序数据即网络输入数据，t代表时间序列数据的时刻.Ft表示第t时刻时序数据对应的编码器层的输出值，Ot为t时刻输入数据对应的解码器层输出值即网络模型的输出值.

3.2.2 双路加权GRU神经网络

GRU网络作为循环神经网络的一种变体，和传统循环神经网络一样考虑了历史时刻的状态对当前状态的影响，同时引入门控机制来控制信息的积累速度，有选择的加入新的信息和遗忘之前累积的信息，能够有效解决传统循环神经网络训练过程中的长程依赖问题[20].而本模型使用的BiGRU在训练过程中不仅考虑了历史时刻的状态，还同时考虑了未来时刻的状态对当前时刻的影响，使得网络单元输入信息更加全面，提高模型的预测能力.BiGRU在单向GRU基础上增加了一个隐含单元，用来额外接收未来方向的状态值.BiGRU的输出值由两个方向的隐含单元输出值结合得出.BiGRU网络结构如图3所示.

图3 BiGRU结构图Fig.3 BiGRU structure diagram

图3中，ft表示历史方向训练过程中t时刻隐含层的状态，f′t表示未来方向训练过程t时刻隐含层的状态.两个方向上的神经单元都是GRU,Ft是一个完整BiGRU单元的最终输出值，由两个方向上的GRU单元输出值共同决定.本文的预测模型使用加权方式结合两个方向的状态，避免传统的累加带来的模型不稳定和预测低精度问题.加权公式如下所示：

(7)

式中，q为权重系数.本模型中q由SDE算法寻优确定.过去和未来两个方向共同训练，并由加权方式组合每个方向的GRU值，构成一个完整的加权BiGRU神经网络模型.

BiGRU神经网络的训练和预测过程都分为两个方向进行，每一个方向都可看作一个传统的单向GRU网络[21].不管是历史方向还是未来方向，隐含层的神经单元都是GRU.GRU的内部结构如图4所示.

图4 GRU内部结构图Fig.4 GRU internal structure diagram

rt=σ(Wr[ft-1,Xt]+br)

(8)

ut=σ(Wu[ft-1,Xt]+bu)

(9)

(10)

(11)

式中，Wr,Wu,Wf,br,bu,bf为GRU网络单元运算过程中的权值和阈值，本文的预测模型中由SDE算法寻优获得它们的初始值.

双路加权BiGRU神经网络的基础运算单元GRU与同样应用广泛的门控网络单元LSTM相比较，它不对记忆细胞有额外的处理和计算，它的记忆细胞值就是GRU单元输出值，而且不引入遗忘门，只用一个更新门就能巧妙控制输入和遗忘之间的平衡，简化了门控网络模型且提高了训练速度.

3.3 预测模型的工作流程

本文提出的融合SDE算法和加权BiGRU神经网络的股价走势预测模型的工作流程如下：

1)获取股票时间序列数据集，并对数据进行归一化预处理操作，获得同一特定区间的数据值.

2)运用SDE算法多次迭代和进化进行参数寻优，获得加权BiGRU结构中初始权值、初始阈值以及权重系数的最优组合.

3)使用SDE优化的参数完善加权BiGRU网络结构，并通过多次仿真确定其他的运行超参数.

4)应用训练数据集迭代训练网络，最小化网络损失函数值及误差.

5)使用迭代训练好的预测模型对预测数据集进行测试，计算预测模型各评价指标值，并与传统模型进行对比分析.

4 仿真实验与结果分析

4.1 实验环境说明与数据预处理

本文的预测模型是基于python的开发环境进行仿真实验的，主要采用了深度学习和机器学习框架Tensorflow和Sklearn来应用SDE算法以及构建、训练、测试网络模型，最终完成预测模型的搭建与仿真.仿真实验所需的数据集均来自雅虎财经官方网站，其中训练数据集选择的是上证的代码区间在600600-601000的股票数据，测试数据集选择代码区间为603500-603998的股票数据以及上证指数数据.个股及指数都采用2017年11月29日-2020年5月22日的数据进行训练，共601个开盘日.每一支股票的数据就是一个独立的数据集，本模型采用前两天的输入数据来预测后一天的开盘价，即时间步长为2，每两天的数据则是一个输入样本，故训练网络时的每个数据集的有效输入样本为599个.每个开盘日的输入数据包括：开盘价、最高价、收盘价、最低价、成交量.

不同量纲的数据会让训练和预测的结果紊乱且失真，而且预测网络的激活函数的值域也在特定范围内，因此本模型对输入的不同维度的数据进行预处理即归一化，采用最大最小归一化的方法，将所有数据全部映射到[-1,1]的区间.这样可以避免不同的股票数据因为量纲相差过大而导致最终的开盘价预测走势产生巨大的波动或者与真实走势有过大的差距，同时与预测网络的函数值域相契合.归一化的公式如式(12)所示：

(12)

式中，S表示归一化后的数据，X表示输入的样本数据中某一个维度的数据，Xmin表示某维度输入数据中的最小值，Xmax表示某维度输入数据中的最大值.

4.2 超参数和评价指标的确立

本文的预测模型中，网络结构中的初始权阈值和权重系数由SDE寻优获得，网络结构和SDE算法的其他超参数由多次实验仿真确定.为了将本模型与传统模型进行对比，不同的模型中的相同结构使用相同的超参数.经过大量仿真实验，本预测模型的超参数设置如表1所示.

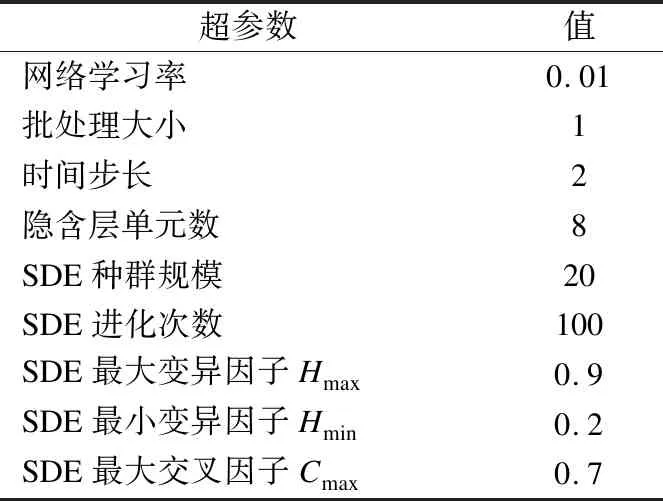
表1 超参数的设置Table 1 Setting of hyperparameters

本文选择3种评价指标作为模型对比分析的依据，分别为MAE(平均绝对误差)、RMSE(均方根误差)和R2(决定系数).MAE能直观看到真实值与预测值之间的差距，RMSE能敏感的捕获误差变化，R2用于判断网络的拟合程度，可作为预测能力指标，R2值越大，则模型预测能力越强，预测精度越高.3个指标的运算公式如式(13)-式(15)所示：

(13)

(14)

(15)

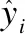
4.3 实验结果分析与对比

将股票数据集的各样本输入进本文提出的优化预测模型中进行训练，全部训练完之后，选取其中代码为600652的股票数据集的训练结果进行展示，图5展示了该个股数据集在预测模型中的训练过程，最小损失值就是训练过程中的最小误差值.通过图5可以观察到训练过程的前期使用较少样本数能使损失值迅速降低，训练到500样本数左右损失值收敛至稳定的区间，且损失值达到极低水平，这说明本模型有着较高的误差收敛性能.

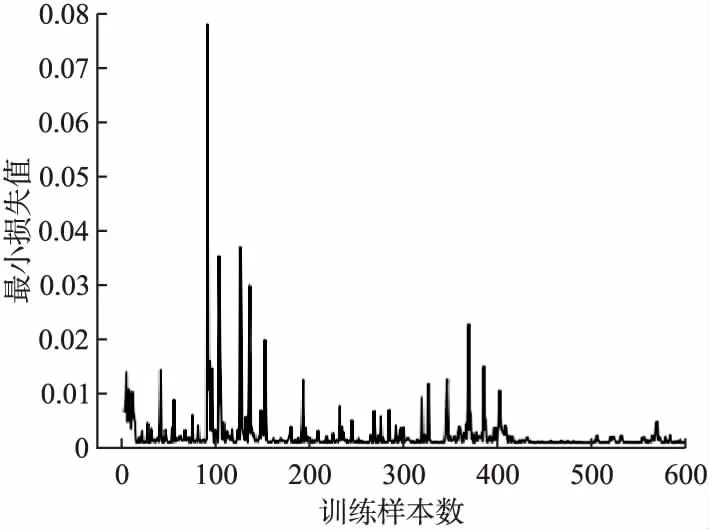
图5 预测模型的训练损失值Fig.5 Training loss of the prediction model

通过模型的迭代训练，不断更新和优化网络权值和阈值，使得网络损失值达到全局最小，得到可供预测的预测模型.使用预测数据集对模型进行多次测试，并将代码为603396的个股以及上证指数的价格预测走势作为预测结果进行展示，分别由图6和图7展示.从图片可以看到，不管是个股还是

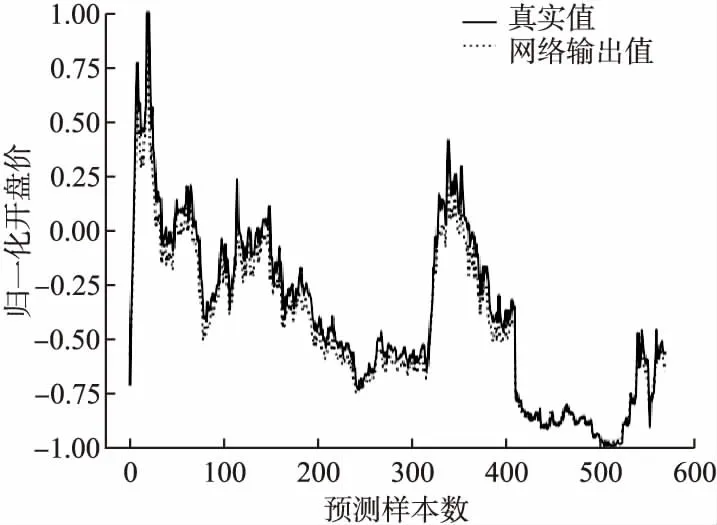
图6 预测模型的预测结果(个股)Fig.6 Forecasting results of prediction model(Stock)

图7 预测模型的预测结果(上证指数)Fig.7 Results of prediction model(Shanghai composite index)

上证指数，本文的预测模型都能将股价预测走势与真实走势高程度的拟合，达到很高的预测效果.总体来看，对指数的拟合程度高于个股，因为影响个股股价的因素更复杂和多元，而指数的走势更能反映股市整体规律，对于模型来说更容易把握整体规律.

为了验证本文的预测模型的优势，将其分别与BP网络模型、LSTM网络模型、单向GRU网络模型、BiGRU网络模型这几种预测模型进行比较，对比分析MAE、RMSE和R23种预测评价指标在各预测数据集下的平均值.由表2可以发现，这几种预测模型都具备一定的预测能力，但是各模型的表现有着较大的差异.LSTM模型及单向的GRU模型与BP网络模型相比，3种预测指标值均表现更优，这是因为LSTM和GRU增添了循环单元和门控机制，使网络具备记忆功能，且有效解决长程依赖和梯度消失等问题，促使预测能力得到进一步提升.作为LSTM模型的变体，单向GRU模型的预测指标与其相比没有优势，因为GRU的改良特点主要在于优化结构以及提升训练速度.而同时考虑历史方向和未来方向的BiGRU网络模型，与LSTM和单向GRU模型相比，预测指标值得到明显优化，因为 BiGRU同时对其过去和未来数据的影响进行处理，充分考虑了多方向的因素对预测结果的影响.本文引入SDE算法进行参数寻优的加权BiGRU优化模型则在基础BiGRU模型基础上进一步提升了预测性能.由表2实验数据分析可知，与上述4种模型中表现相对较优的BiGRU模型相比，本文的模型不论是预测误差指标MAE和RMSE还是预测能力指标R2，都有着显著的提升.其中，MAE降低了17%，RMSE降低了24%，R2提高了1.7%.由此可知，本文提出的优化预测模型能够在传统的各预测模型基础上使预测误差进一步缩小，预测能力即预测精度也得到进一步提升，充分验证了本文预测模型的性能优越性.

表2 本文预测模型与其他传统模型的比较Table 2 Comparison of the prediction model to others

5 结 语

本文提出的融合SDE算法和双路加权门控循环神经网络的股价走势预测模型，通过SDE寻优求得全局最优的BiGRU网络初始权阈值和权重系数，构成优化的加权BiGRU神经网络预测模型.SDE寻优可避免网络训练过程的局部最优情况，加权BiGRU通过双路门控机制，有选择的考虑过去和未来重要节点的影响，不仅能避免网络长程依赖问题，还能充分考虑股票时序数据受重要时间节点影响的特性.经过反复多次的试验，本预测模型达到了预期的优化效果.通过与传统神经网络预测模型进行对比，可以发现优化的预测模型较大程度减小了股价走势预测的误差，走势预测的准确度也大大增加.本文的优化预测模型通过增加较小的计算成本而较大程度提高了股价走势预测的准确度，所以该优化模型具有较高的社会使用和科学研究价值.未来的研究会考虑增加一些其他的影响因子到预测模型中去，以求实现更高的预测精度和使用效率，同时实现更低的计算成本.