协作机器人逆运动学形式化建模与验证
2021-07-08王国辉施智平张倩颖邵振洲
王 畅,王国辉,施智平,关 永,张倩颖,邵振洲
(首都师范大学 信息工程学院,北京 100048)
1 引 言
随着人工智能和计算机的快速发展,工业机器人被广泛地应用于各个领域中,在电子电气、汽车制造、物流运输、食品加工等行业都有着不同的贡献.当前,人机协作型机器人成为工业机器人领域里备受关注的类型之一.与传统的工业机器人相比,协作型机器人成本低廉、场景多元、操作便捷.作为工业机器人新兴领域,协作型机器人虽然有许多的优点,给人类的生活带来极大的便利,但是随之而来的安全问题也越来越受到重视.传统工业机器人致死的新闻屡见不鲜,例如:2015年德国大众汽车制造厂中一个机器人杀死了一名人类工作人员.在安装和调制机器人过程中,该工作人员被机器人击中胸部导致其被碾压在金属板上,当场死亡.频发的安全事故表明,即使传统的工业机器人在部署时,还额外安装了安全围栏,也无法避免因机器人突然的“暴走”而引发的灾难性事故,因此人机协作机器人的安全性问题成为人们关注的焦点,也对其安全性提出了更高的要求.
机器人逆运动学的建模与求解是决定其安全性的必要因素之一.机器人的逆运动学是指根据所要到达的目标位置来确定机器人各关节的运动变量[1].目前关于机器人模型的方法主要有D-H参数法[2]和旋量法[3]两种.其中,D-H参数法是一种为关节链中的每一连杆建立坐标系的矩阵方法[4].但是对于相邻关节平行的机器人,会出现模型参数不连续而导致的奇异性问题[5].相较于传统的D-H参数法,旋量法从整体上描述刚体的运动,它无需建立各连杆坐标系,只建立惯性基坐标系和末端工具坐标系,从而避免了用局部坐标系描述时所造成的奇异性[6].目前,也有许多学者基于旋量法对协作型机器人逆运动学求解进行研究[7].例如:Igor Dimovsk[8]
等基于旋量法描述了一些常见的Paden-Kahan子问题在机器人逆运动学求解中的应用.然后基于这些常见的子问题扩展出了一些新的子问题.Chen[9]等基于指数积公式和分类的子问题对机器人逆运动学求解.但是,这些研究还都停留在使用传统的测试用例方法对机器人逆运动学进行验证.
目前,机器人模型的验证也有许多不同的方法.常见的有:利用MATLAB对机器人模型进行模拟与仿真,以及用Maple、Mathematica等数学软件验证机器人的代数系统.然而这些软件自身的短板和漏洞,常常会导致数值计算的误差或符号计算的错误,从而无法实现机器人逆运动学正确的求解[10].例如:计算仿真系统(如MATLAB)因为浮点表达的天然局限无法提供100%精确的结果[11];计算机代数系统(如 Maple、Mathematica等)虽然支持符号运算从而可以得到精确结果,但是其在边界条件的处理上存在短板(如x≠0是表达式1/x的边界条件),同时计算机代数系统内核中的符号计算算法也尚未得到验证,可能因其自身存在漏洞而影响其验证结果的精确性[12].因此,提出使用形式化的方法对其进行验证,可以克服上述传统方法的局限性,从而保证机器人逆运动学求解模型的可靠性.
形式化验证是基于计算机的数学分析技术,用严谨的数学逻辑来验证模型的可靠性.高阶逻辑定理证明是形式化验证中的一种,它是一种交互式验证方法,主要涉及到基于高阶逻辑的系统数学建模和基于演绎推理的系统性能验证,它将系统与规范都描述成数学逻辑的形式,从公理出发寻求描述,证明数学模型的准确性与可靠性[13].
由于机器人逆运动学的建模与求解是决定其安全性的必要因素之一.然而,目前使用形式化方法对机器人运动学进行建模与验证的案例还屈指可数.2017 年日本国家先进工业科学研究院信息技术研究所Affeldt[14]等人在COQ 定理证明器中,实现了罗德里格斯公式等数学理论定理库的构建,完成了SCARA 型串联机器人运动学模型的构建与验证.巴基斯坦伊斯兰堡国立科技大学Adnan Rashid[15]等采用旋量理论对细胞注射机器人动力学分析进行了形式化验证.2020年首都师范大学陈琦[16]等采用定理证明的方法实现了平面并联机构的相关数学理论的高阶逻辑表达,验证了平面并联机构运动学分析的正确性和求解方法的可靠性.但是,对机器人逆运动学形式化建模与验证的工作还是空白.因此本文在旋量高阶逻辑定理证明库的基础上,实现指数积[17]和Paden-Kahan子问题(subprob-R)等数学理论的高阶逻辑表达,在交互式定理证明器HOL-Light[18]中对6R协作型机器人逆运动学建模与求解过程进行形式化验证.本文的主要贡献如下:
·基于旋量理论,对刚体运动的运动旋量的指数形式进行形式化建模;
·对Paden-Kahan子问题(subprob-R)进行形式化建模;
·对6R型协作机器人逆运动学的求解过程进行形式化分析与验证.
2 预备知识
本节将简要介绍定理证明器HOL-Light和工具中常用符号的含义,然后分析6R型协作机器人的经典结构.
2.1 HOL-Light基础
HOL-Light是一种基于LCF理论的定理证明器[19].它的实现语言为元语言(ML),广泛地应用于理论形式的数学证明地构造[20].在定理证明器中,必须确保已经建立了相关的数学定理库,然后才可以进行定理证明[21].目前,在定理证明器HOL-Light中已存在大量的定理库例如旋量、多元分析、实数、超越等.这些定理库为本文的后续工作提供了强大的支持.因此,本文选择使用定理证明器HOL-Light对机器人逆运动学进行形式化建模.为了方便对本文其它部分的理解,这里对定理证明器HOL-Light中一些常用的符号和函数进行了说明,如表1所示.

表1 HOL-Light中的符号与函数
2.2 人机协作机器人经典结构
与发展了几十年的工业机器人相比,协作机器人最大的突破在于它可以直接与人类并肩合作,而无需使用安全围栏进行隔离,这种方式不仅减少了人和机器人之间的距离,大大减少了工位所占的面积,更重要的是可以充分结合人和机器的优势,彼此取长补短,让机器人辅助人类去完成高重复性、高精度的工作,而人类则解决灵活性高、不断优化的工作.例如,在装配高精度的重型零部件时,人机协作便凸显出其将人和机器结合在一起的优势.正是由于人与协作机器人的紧密工作关系,使得它的安全性问题受到格外的重视.
常见的协作型机器人如:UR、OUR等系列都是关节均为旋转关节的6R型机器人,其结构图如图1所示.其中1、2关节,4、5关节和5、6关节的轴线分别相交于一点,相邻的2、3、4关节相互平行.在进行刚体变换时,它仅进行旋转运动,没有平移.

图1 人机协作机器人旋量坐标系
3 刚体运动与求解方法的形式化
在本节中,首先实现刚体运动旋量指数形式相关内容的高价逻辑表达.然后基于旋量理论,构建Paden-Kahan子问题(subprob-R)的形式化模型.
3.1 刚体运动旋量指数形式


定义1.算子“∧”
|-∀screw_2_matrixξ=lambdaij.ifi<=3∧j<=3then(vec3_2_ssm(FSTξ))$i$jelseifi<=3∧j=4then(SNDξ)$ielse&0

定义2.位置的齐次变换矩阵
|-∀homo_transxR=lambdaij.ifi=(dimindex(:N)+1)∧~(j=dmindex(:N)+1)then&0elseifi=(dimindex(:N)+1)∧(j=dmindex(:N)+1)then&1eslseif~(i=(dimindex(:N)+1) )∧(j=dmindex(:N)+1)thenx$jelseR$i$j
定义2中homo_transxR是位置的齐次矩阵在HOL-Light中的表示形式,其中的R为三阶矩阵,x为三维列向量.

定义3.速度的齐次矩阵
|-∀homo_trans_tangentdxdR=lambdaij.ifi=(dimindex(:N)+1)then&0elseif~(i=dimindex(:N)+1)∧(j=dimindex(:N)+1)thendx$ielsedR$i$j
定义3中的homo_trans_tangentdxdR就是速度的齐次矩阵在HOL-Light中的表达形式,其中dR为三阶矩阵,dx为三维列向量.
由定义1可知,运动旋量和速度的齐次矩阵的数学含义是相同的,但其描述形式是不同的.因此,需要在定理证明器HOL-Light中对其数学含义相同的属性进行证明,该过程被形式化描述为定理1.
定理1.运动旋量的矩阵表达形式
|-∀s.screw_2_matrixξ=homo_trans_tangent(SNDξ)(vec3_2_ssm(FSTξ))
定理1证明了运动旋量可以表示为速度的齐次矩阵形式.

定理2.当仅进行平移时的旋量的指数形式
|-∀ξθ.FSTξ=vec0⟹matrix_exp=(θ%%screw_2_matrixξ)=homo_trans(θ%(SNDξ))(mat1)
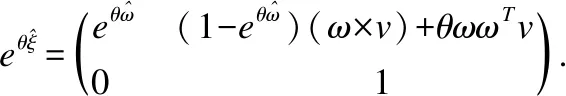
定理3.当既平移又旋转时的运动旋量的指数形式
|-∀ξθ.norm(FSTξ)=&1⟹matrix_exp=(θ%%screw_2_matrixξ)=homo_trans((mat1-matrix_exp(θ%%vec3_2_ssm(FSTξ)))**((FSTξ)cross(SNDξ) )+θ%%(vec3_2_ssm(FSTξ)**(SNDξ)))(matrix_exp(θ%%vec3_2_ssm(FSTξ)))
3.2 Paden-Kahan子问题(subprob-R)
基于Kahan[22]的研究,Paden[23]提出将几何求解方法应用于机器人逆运动学中.一般情况下,运动学求逆解的子问题是指涉及的运动旋量个数不超过3,且具有明确的几何意义和数值稳定性[1].根据子问题中运动旋量的个数与性质可以将其分为11种子问题,例如:描述刚体旋转的subprob-R、描述刚体平移的subprob-TT以及描述刚体旋转和平移相结合的subprob-RT(或subprob-TR)等,这些统称为Paden-Kahan子问题[8].其主要思想是将复杂的机器人运动学逆解分解为若干个具有明确几何意义的逆解子问题,然后逐一解决,即将复杂的运动分解为几个连续的简单运动[24].在用旋量法对机器人求逆解的过程中,经常会遇到这些子问题,现在越来越多的人关注到这个问题并对其进行研究.

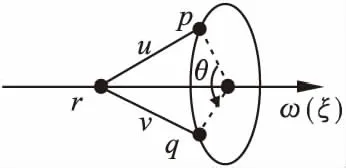
图2 子问题(subprob-R)
定理4.Paden-Kahan子问题(subprob-R)的解
|-∀θωruu′vv′pqξ.--(pi/&2)<θ∧θ<(pi/&2)∧ξ=(ω,rcrossω)①
u=p-r∧v=q-r∧normω=&1∧②
u′=u-(vec3_vtrans(FSTξ)**u)∧③
v′=v-(vec3_vtrans(FSTξ)**v)∧④
matrix_exp(θ%%screw_2_matrixξ)**(homo_point(mk_pointr))=(homo_point(mk_pointr))∧⑤
matrix_exp(θ%%screw_2_matrixξ)**(homo_point(mk_pointp))=(homo_point(mk_pointq))∧~(u′=0)⟹⑥
θ=atn((ωdot(u′crossv′ ))/(u′dotv′))
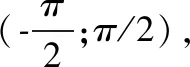
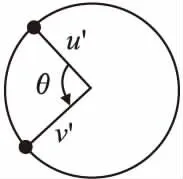
图3 子问题(subprob-R)投影

(1)

(2)
将公式(2)带入子目标后,可得公式(3).
(3)
然后,再引入一个子目标ωωTu′=0,证明其成立.由于u′和u存在关系式:u′=u-ωωTu.利用重写策略将该关系式写入子目标中,可得ωωTu′=ωωTωωTu′.通过使用化简策略可将公式(3)化简为公示(4).

(4)
在定理证明器中通过再次使用重写策略将公式(4)重写入公式(1),经过化简策略即可证明子目标成立.最终证明Paden-Kahan子问题(subprob-R)是成立的.
4 6R协作机器人逆运动学形式化验证
4.1 正向运动学形式化建模
在对机器人进行逆运动学求解时,需要先根据图1的坐标系对机器人进行运动学建模.
各关节单位矢量ωi,轴上一点ri和运动旋量分别构建如下[5]:
图1中机器人对应的初始位姿可由公式(5)描述.
(5)
公式(5)中的初始位姿可被形式化定义为定义4.
定义4.初始位姿
|-∀gst_initialx=homo_transx(mat1)
在定义4中,mat1表示的是三阶单位矩阵,x为三维列向量.
6自由度串联机器人正向运动学的数学公式如公式(6)所示.
(6)
其正向运动学的形式化模型如定义5所示.
定义5.正向运动学
|-∀gstξ1ξ2ξ3ξ4ξ5ξ6θ1θ2θ3θ4θ5θ6x=matrix_exp(θ1%%screw_2_matrixξ1)**matrix_exp(θ2%%screw_2_matrixξ2)**matrix_exp(θ3%%screw_2_matrixξ3)**matrix_exp(θ4%%screw_2_matrixξ4)**matrix_exp(θ5%%screw_2_matrixξ5)**matrix_exp(θ6%%screw_2_matrixξ6)**(gst_initialx)
4.2 逆运动学求解模型验证
4.2.1 验证关节角θ1
第1个关节到末端执行器的刚体运动变化过程可由公式(7)描述.
(7)
该过程形式化模型如定义6所示.
定义6.从第1个关节到末端执行器的刚体变换的运动过程
|-∀gst1ξ1ξ2ξ3ξ4ξ5ξ6θ1θ2θ3θ4θ5θ6=matrix_exp(θ1%%screw_2_matrixξ1)**matrix_exp(θ2%%screw_2_matrixξ2)**matrix_exp(θ3%%screw_2_matrixξ3)**matrix_exp(θ4%%screw_2_matrixξ4)**matrix_exp(θ5%%screw_2_matrixξ5)**matrix_exp(θ6%%screw_2_matrixξ6)
根据定义6,可得到第1个关节到末端执行器的刚体运动变化过程,这个运动变换过程的代数运算可由公式(8)描述.
(8)
根据公式(7)与公式(8)相等的属性.该刚体的运动过程可以被形式化建模为定理5.
定理5.从第1个关节到末端执行器的刚体变换的运动过程的代数运算
|-∀ξ1ξ2ξ3ξ4ξ5ξ6θ1θ2θ3θ4θ5θ6x
gstξ1ξ2ξ3ξ4ξ5ξ6θ1θ2θ3θ4θ5θ6x**(matrix_inv(gst_initialx))=gst1ξ1ξ2ξ3ξ4ξ5ξ6θ1θ2θ3θ4θ5θ6
在定理5中,假设ξ1,ξ2,ξ3和ξ4是具有零节距的单位运动旋量,验证了gst-1(0)同乘公式(6)两边可得到gst(1)的过程.
若设机器人第5、6关节轴线相交于点p56,用该点同时右乘公式(8)两边,并根据位置不变原则,可得:
(9)
公式(9)表示点p56分别绕着前4个关节轴线做旋转运动,最终到达目标位置p1,其几何表示如图4所示.
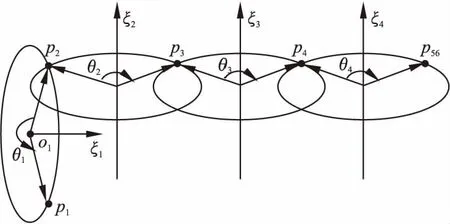
图4 前4关节螺旋运动
从图4可知,当机器人位于初始位姿时,点p56分别围绕第4、3、2关节轴线转动角度θ4、θ3、θ2到达p2点位置.最后该点再围绕第1关节轴线ξ1转动角度θ1到达目标位置p1.求解角度θ1的关键是求出点p2的坐标,那么该点可通过已知的p56和p1两点来求得.则根据图4可得到公式(10).
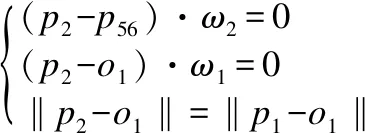
(10)
由于各变量的值分别为p1=(px,py,pz),ω1=(0,0,1),ω2=(1,0,0),o1=(0,0,pz)和p56=(d4,0,a2+a3+d5).结合公式(10)即可求得点p2的坐标如公式(11)所示.
(11)
推导点p2坐标的过程可形式化描述为定理6.
定理6.p2点坐标
|-∀o1ω1ω2p1p56p2pxpypza2a3d4.
(p2-p56)dotw2=&0∧(p2-01)dotω1=&0∧norm(p2-01)=norm(p1-o1) ∧p1=vector[px;py;pz]∧ω1=vector[&0;&0;&1]∧ω2=vector[&1;&0;&0]∧o1=vector[&0;&0;pz]∧p56=vector[d4;&0;a2+a3+d4]⟹(p2$1=d4∧p2$3=pz∧p2$2pow2=(pxpow2+pypow2-d4pow2))
点p2在第1关节中的螺旋运动可表示为公式(12).
(12)
根据已知的各个变量的坐标值,通过应用Paden-Kahan子问题(subprob-R),可得θ1的值为公式(13).
(13)
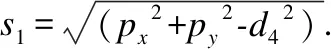
根据Paden-Kahan子问题(subprob-R)求解θ1值的过程可形式化描述定理7.
定理7.验证关节角度θ1
|-∀p1p2ω1r1o1pxpypzs1d4ξ1θ1.
p1=vector[px;py;pz]∧p2=vector[d4;b1;pz]∧ω1=vector[&0;&0;&1]∧ξ1=(ω1;vec0)∧o1=vector[&0;&0;pz]∧~(d4=0)∧--(pi/&2)<θ1∧θ1<(pi/&2)∧norm(p2-01)=norm(p1-o1)∧matrix_exp(θ1%%screw_2_matrixξ1)**(homo_point(mk_pointp2))=(homo_point(mk_pointp1))⟹θ1=atn((--(px*s1)+d4*py)/(d4*px+py*s1))
其中,atn表示的是反正切函数arctan.其证明过程如下,首先使用特殊化策略引入Paden-Kahan子问题(subprob-R),然后结合旋量指数形式定理(定理3),运用化简策略SIMP_TAC实现定理7的证明,该策略的主要功能是通过已有定理进行有条件的上下文重写来简化目标.
4.2.2 验证关节角θ5和θ6
第2个关节到末端执行器的刚体运动变化过程可由公式(14)描述.
(14)
该过程可被形式形式化描述为定义7.
定义7.从第2个关节到末端执行器的刚体变换的运动过程
|-∀gst2ξ2ξ3ξ4ξ5ξ6θ2θ3θ4θ5θ6=matrix_exp(θ2%%screw_2_matrixξ2)**matrix_exp(θ3%%screw_2_matrixξ3)**matrix_exp(θ4%%screw_2_matrixξ4)**matrix_exp(θ5%%screw_2_matrixξ5)**matrix_exp(θ6%%screw_2_matrixξ6)

在公式(6)中,可令gst(θ)如公式(15)所示.
(15)
根据公式(14)可得如公式(16)所示的关节角θ5和θ6与其他变量之间关系,其形式化模型如定理8所示.
(16)
定理8.关节角θ5和θ6与其他变量之间关系形式化模型
|- ∀ξ1ξ2ξ3ξ4ξ5ξ6xθ1θ2θ3θ4θ5θ6d4d5a2a3R11R21R31R12R22R32R13R23R33t1t2t3.
gstξ1ξ2ξ3ξ4ξ5ξ6θ1θ2θ3θ4θ5θ6x=homo_trans(vector[t1;t2;t3])(vector[vector[R11;R12;R13];vector[R21;R22;R23];
vector[R31;R32;R33])∧x=vector[d4;&0;a2+a3+d5]∧ξ1=(vector[&0;&0;&1],vector[&0;&0;&0] )∧ξ2=(vector[&1;&0;&0],vector[&0;&0;&0] )∧ξ3=(vector[&1;&0;&0],vector[&0;a2;&0] )∧ξ4=(vector[&1;&0;&0],vector[&0;a2+a3;&0])∧ξ5=(vector[&0;&0;&1],vector[&0;--d4;&0] )∧ξ6=(vector[&1;&0;&0],vector[&0;a2+a3+d5;&0] )⟹cosθ5=R11*cosθ1+R21*sinθ1∧sinθ5*sinθ6=R13*cosθ1+R23*sinθ1∧--(sinθ5*cosθ6)=R12*cosθ1+R22*sinθ1∧sinθ5*sin (θ2+θ3+θ4)=R31∧sinθ5*cos(θ2+θ3+θ4)=R21*cosθ1-R11*sinθ1
定理8验证了各个变量之间的关系是准确的.
通过化简公式(16)可得公式(17)-(19),即为关节角θ5,θ6和θ2+θ3+θ4的解析模型.
(17)
θ6=arctan((s3/sinθ5)/(-s4/sinθ5))(sinθ5≠0)
(18)
θ2+θ3+θ4=arctan((R31/sinθ5)/(s5/sinθ5))(sinθ5≠0)
(19)
式中,s2=R11*cosθ1+R21*sinθ1,s3=R13*cosθ1+R23*sinθ1,s4=R12*cosθ1+R22*sinθ1,s5=R21*cosθ1-R11*sinθ1.
根据变量之间的已知关系,关节角θ5,θ6和θ2+θ3+θ4解析模型的形式化验证过程描述如定理9所示.
定理9.验证关节角θ5和θ6
|-∀θ1θ2θ3θ4θ5θ6s2s3s4s5R11R21R31R12R22R13R23.
~(sinθ5=&0)∧--(pi/&2)<θ6∧θ6<(pi/&2)∧--(pi/&2)<(θ2+θ3+θ4)∧(θ2+θ3+θ4)<(pi/&2)∧s2=R11*cosθ1+R21*sinθ1∧s3=R13*cosθ1+R23*sinθ1∧s4=R12*cosθ1+R22*sinθ1∧s5=R21*cosθ1-R11*sinθ1∧cosθ5=R11*cosθ1+R21*sinθ1∧sinθ5*sinθ6=R13*cosθ1+R23*sinθ1∧--(sinθ5*cosθ6)=R12*cosθ1+R22*sinθ1∧sinθ5*sin(θ2+θ3+θ4)=R31∧sinθ5*cos(θ2+θ3+θ4)=R21*cosθ1-R11*sinθ1⟹(&0<θ5∧θ5<(pi/&2)⟹θ5=atn((sqrt(&1-s2pow2))/b2))∧(--(pi/&2)<θ5∧θ5<&0⟹θ5=atn(--(sqrt(&1-s2pow2))/s2))∧θ6=atn((s3/(sinθ5))/(--(s4)/sinθ5))∧(θ2+θ3+θ4)=atn((R31/sinθ5)/(s5/(sinθ5)))
根据已知的变量之间的关系,首先使用策略UNDISCH_TAC把假设列表中条件改写为目标的前件,然后结合策略DISCH_THEN(MP_TACoSYM)使得目标前件中等价条件的两侧互换位置,最后使用库中已有定理化简证明定理9.
4.2.3 验证关节角θ2,θ3和θ4
第3个关节到末端执行器的刚体运动变化过程可由公式(20)描述.
(20)
该过程的形式化描述如定义8所示.
定义8.从第3个关节到末端执行器的刚体变换的运动过程
|-∀gst3ξ2ξ3ξ4θ2θ3θ4=matrix_exp(θ2%%screw_2_matrixξ2)**matrix_exp(θ3%%screw_2_matrixξ3)**matrix_exp(θ4%%screw_2_matrixξ4)

(21)
根据公式(20)和公式(21),可以得到公式(22).
(22)
式中t7=t5-(θ2+θ3)sin(θ2+θ3+θ4),t8=t6+(a2+a3)cos(θ2+θ3+θ4).结合公式(21)和公式(22)即可求得θ2和θ2+θ3的解.关节角θ2,θ3和θ4与各个变量之间的关系可形式化描述为定理10.
定理10.各个变量之间几何关系形式化模型



通过定理10验证了各个变量之间的关系是准确的,然后可求得θ2和θ2+θ3的解如公式(23)和公式(24)所示.

(23)
(24)
其中,A=2a2t7,B=2a2t8,C=a32-a22-t72-t82,s6=a2sinθ2+t7,s7=t8-a2cosθ2.
关节角θ2和θ2+θ3的形式化验证过程如定理11所示.
定理11.验证关节角θ2和θV2+θ3
|-∀θ2θ3a2a3t7t8s6s7ABC.
--(pi/&2)<θ2∧θ2<(pi/&2)∧--(pi/&2)<θ2+θ3∧θ2+θ3<(pi/&2)∧--a3*sin (θ2+θ3)-a2*sinθ2=t7∧a3*cos (θ2+θ3)+a2*cosθ2=t8∧A=&2*a2*t7∧B=&2*a2*t8∧C=(a3)pow2-(a2)pow2-(t7)pow2-(t8)pow2∧s6=a2*sinθ2+t7∧s7=t8-a2*cosθ2∧~(a2=&0)∧~(t7=&0)∧~(t7pow2+t8pow2=&0)∧--(pi/&2)<(atn(t8/t7)+atn((t7*sinθ2-t8*cosθ2)/(t7*cosθ2-t8*sinθ2))))∧(atn(t8/t7)+atn((t7*sinθ2-t8*cosθ2)/(t7*cosθ2-t8*sinθ2))))<(pi/&2)⟹(&0<(&2*t7*a2*cosθ2+&2*t8*a2*sinθ2)⟹(θ2=atn(B/A)+atn(C/(sqrt((Apow2)+(Bpow2)-(Cpow2)))))∧((&2*t7*a2*cosθ2+&2*t8*a2*sinθ2)<&0⟹(θ2=atn(B/A)+atn(C/(--(sqrt((Apow2)+(Bpow2)-(Cpow2)))))∧θ2+θ3=atn((--(s6)/a3)/(s7/a3))
首先引入变量C和sqrt((Apow2)+(Bpow2)-(Cpow2))的最简形式的子目标,然后结合重写策略REWRITE_TAC,化简策略SIMP_TAC实现定理11的证明.
通过公式(19)、公式(23)和公式(24),结合公式(25)和公式(26)即可得到θ3和θ4的解.在HOL-Light中,可以直接利用重写策略和实数自动证明策略完成θ3和θ4的求解过程的形式化验证.
θ3=(θ2+θ3)-θ2
(25)
θ4=(θ2+θ3+θ4)-(θ2+θ3)
(26)
4.2小节完成了对6R型协作机器人逆运动学各个关节角求解模型的形式化验证,从而确保6R协作机器人逆运动学求解的安全性和可靠性.
5 结 论
本文以旋量理论和指数积公式为基础,通过解析、几何、矩阵理论和Paden-Kahan子问题(subprob-R)对6自由度协作型机器人求逆解过程进行形式化验证.在高阶逻辑定理证明器HOL-Light中,首先基于已有的旋量库,对于缺少的刚体运动旋量的指数形式进行了补充.然后实现了指数积公式和Paden-Kahan子问题(subprob-R)相关理论的高阶逻辑化.最后,结合旋量理论、指数积公式和Paden-Kahan子问题(subprob-R)等相关定理对协作型机器人逆运动学求解模型进行形式化分析与验证.从而确保基于旋量理论的机器人逆运动学求解模型与求解过程的完备性与可靠性,保证机器人工作过程中的安全性.本文的研究内容有效的确保了机器人逆运动学建模和求解过程的可靠性,从而保证了机器人系统的安全性.同时也促进了机器人产业更快更好的发展,为未来协作型机器人逆运动学的形式化分析奠定了基础.
