沥青混合料压实度振动加速度温度关系模型
2021-07-07梁乃兴曹源文向阳开
赵 毅, 杨 臻, 梁乃兴, 曹源文, 向阳开
(1.重庆交通大学 交通土建工程材料国家地方联合工程实验室, 重庆 400074; 2.重庆交通大学 材料科学与工程学院, 重庆 400074; 3.重庆交通大学 土木工程学院, 重庆 400074; 4.重庆交通大学 机电与车辆工程学院, 重庆 400074)
压实度是铺筑材料压实质量控制的关键指标之一[1].如果压实度不足,路面容易出现车辙、松散、坑槽等病害[2].国内外现场压实度传统的测试方法普遍存在检测效率低、检测范围覆盖率低、检测滞后等问题,无法实时、快速、连续地反映道路工程材料的压实质量[3].
目前,路面材料智能压实检测技术蓬勃发展[4-5].振动压路机振动轮与被压材料之间的相互作用较为复杂,压实控制指标能否真实反映道路材料的压实质量成为智能压实的关键技术[6].Yoo[7]基于完全弹性理论建立了振动压路机- 土系统的二自由度动力学模型,为振动压路机智能化发展奠定了理论基础.Pietzsch等[8]提出了机架-振动轮-土的四自由度动力学模型.徐光辉等[9]利用动力学原理和自动测试技术,以振动加速度响应值来评价路基结构的压实状态.Horan等[10]探讨了智能压实技术应用于热拌沥青混合料铺筑质量控制的可行性.Yoon等[11]认为运用智能压实技术可以提高热拌沥青混合料的压实覆盖率和均匀性.Hu等[12]运用智能压路机压实计算值来反映沥青层的压实程度,并分析了温度的影响.Chang等[13]使用配有全球导航卫星系统和加速度测量系统的智能压路机进行压实作业,实现了压实效果实时控制和全覆盖.黄志福等[3]建立了振动加速度与路面材料压实度的关系模型.曹源文等[14]以振动压路机-路面材料二自由度动力学模型为基础,建立了振动压路机振动加速度与路面材料刚度关系模型.综上所述,道路工程智能压实技术仍处于探索研究阶段,且集中于路基压实自动连续检测技术,考虑温度分布的沥青路面沥青层智能压实技术相关研究报道较少.
本文将江西省抚吉高速公路作为试验路段,以二自由度动力学模型为基础,开发沥青混合料振动压实实时分析检测系统.结合沥青混合料摊铺—碾压过程中的温度分布,建立沥青混合料压实度-振动加速度- 温度关系模型来反映被压沥青材料碾压过程的实际物理力学性能,为路面材料压实度的自动连续检测和实时反馈提供理论指导.
1 智能压实测试机理
智能压实技术是基于振动压路机钢轮上加速度传感器,测量和计算得到相应的控制指标,以此来反映路面材料的压实状态[6].因此,建立振动加速度(α)与压实度(K)的关系模型成为智能压实技术需要解决的关键问题.智能压实测试机理如图1所示,振动轮施加压实力于被压材料,而被压材料对振动轮产生反作用力,被压材料越密实,反作用力越大,振动轮相应的加速度也越大.通过加速度传感器测量反作用力,以控制系统处理响应信号,并计算智能压实测试值,从而判断被压材料压实程度.
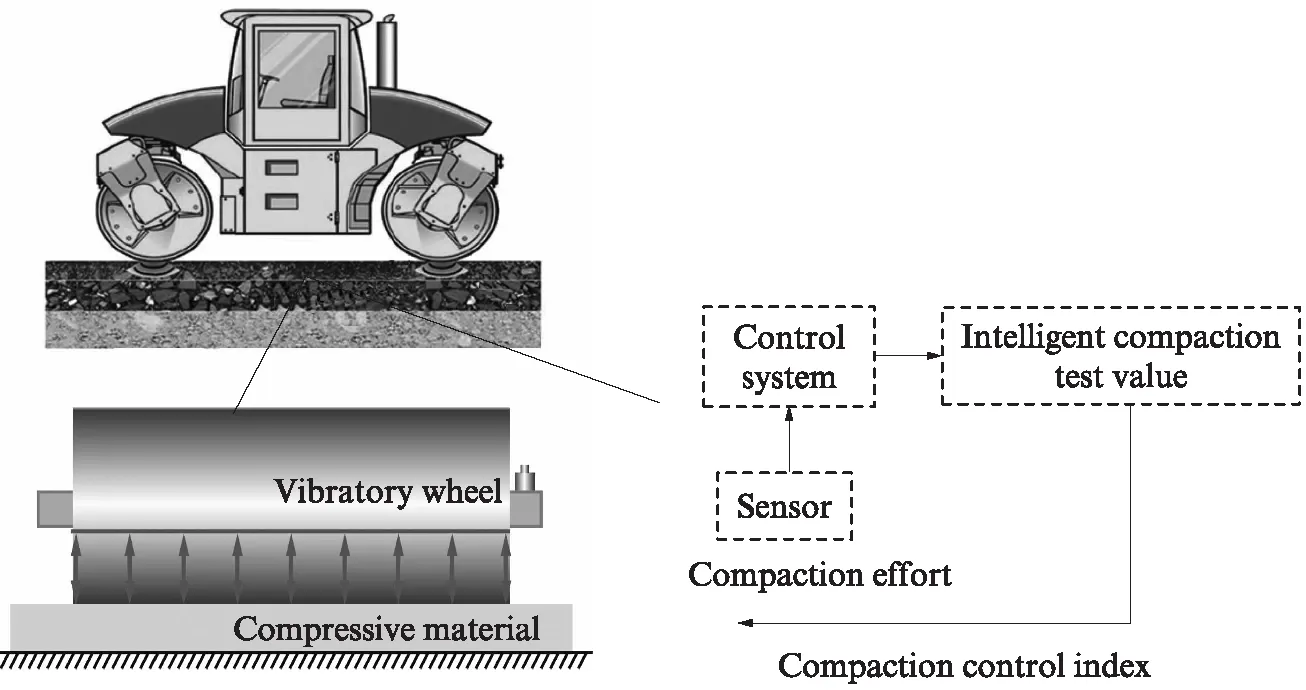
图1 智能压实测试机理
2 振动轮-被压材料系统动力学模型
振动压实是沥青混合料常见的压实方法之一,其原理如图2所示.振动压路机通过偏心块式振动器高速旋转产生的横向离心力来形成激振力,从而使振动轮作用于被压材料[15].振动压实过程是一个复杂的过程,伴随着振动、接触、弹跳和冲击作用,从而使智能压实的精确测量成为一个难题[6].本文以振动轮-被压材料二自由度动力学模型为基础,假设:(1)振动压实过程中机架和振动轮为等效刚体,基本不发生错位和变形,简化为集中质量块.(2)减振器和被压实材料简化为弹簧-阻尼耦合,以描述压实过程中发生的弹性和塑性变形,且弹簧和阻尼元件的质量忽略不计.(3)振动轮的质心在中心位置,简化为平面振动模型.(4)压实力只考虑垂直方向激振力作用.(5)以质量-弹簧-阻尼耦合模型表示振动压实过程中振动轮对被压实材料的压实作用.
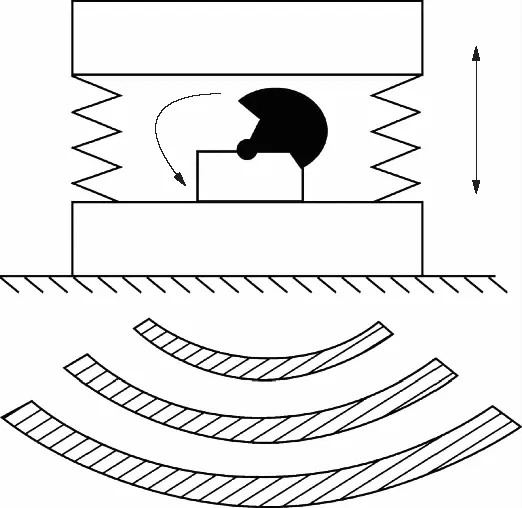
图2 振动压实法原理示意图
振动压路机振动轮-被压材料系统动力学模型如图3所示.图中m1为机架质量,k1为振动轮减振器刚度,c1为振动轮减振器阻尼系数,x1为机架瞬时位移,m2为振动轮质量,F0为激振力,ω为偏心块旋转角速度,Me为静偏心力距,t为作用时间,x2为振动轮瞬时位移,k2为被压材料弹性刚度,c2为被压材料阻尼系数,m3为被压材料质量,x3为随动土体瞬时位移,Fs为接触力.
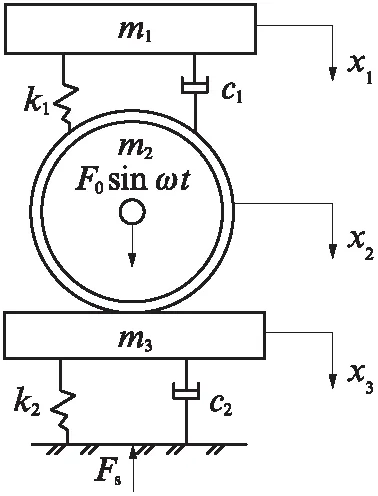
图3 振动轮-被压材料系统动力学模型
沥青混合料振动压实可分为A、B、C 3个阶段[16].A阶段:该阶段产生较大的塑性变形,弹性模量增加,刚度增加,阻尼减小,为荷载-变形阶段;B阶段:该阶段沥青混合料密实度逐渐增大,塑性变形减小,吸收振动能量的能力减弱,产生以弹性变形为主的应力-应变阶段;C阶段:该阶段为刚性的应力-应变状态,路面材料基本压实,变形不再增加.若继续振动压实,则会产生跳振,容易破坏混合料级配和内部结构,应停止压实.
当振动轮-被压材料系统处于A和B阶段时,振动轮与被压材料接触,属于正常压实,未出现跳振,x2=x3,可将m2和m3视作一体进行动力学分析.本文以B阶段作为研究对象,选取m1、m2、m3离开其静平衡位置的位移分别为x1、x2、x3,作为系统运动的坐标.根据牛顿第二定律,振动轮-被压材料系统动力学模型的振动微分方程为:
(1)
(2)
F0=Meω2
(3)
Me=Ffr
(4)
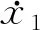
该方程组为二阶线性常系数非齐次微分方程组,其特解为稳定阶段的等幅振动,系统按与激振力相同的频率ω做强迫振动.解微分方程得:
式中:A1=k1-m1ω2;B1=c1ω;A2=k1;B2=c1ω;C=(m2+m3)m1ω4-(m2+m3)k1ω2-m1k2ω2-c1c2ω2+k1k2-m1k1ω2;D=k2c1ω+k1c2ω-(m2+m3)c1ω3-m1c2ω3-m1c1ω3.
由于振动轮受到简谐激振力的作用,因此振动轮的垂直加速度(幅值)可表示为:
(5)
在任一激振力作用下,式(5)中除k2、c2外其他参数均不变.因此,振动轮的垂直加速度只与被压材料的刚度和阻尼有关.
相关资料表明[4],振动压路机作业时,沥青混合料的刚度和阻尼为:
(6)
(7)
式中:e为孔隙比;υ为泊松比;β为振动轮触地角,(°);R为振动轮半径,mm;L为振动轮宽,mm;σ0为平均固结力,N;εd为应变,m/m;ρ为振动压实沥青混合料密度,g/cm3.
由式(6)、(7)可知:振动压实过程中,沥青混合料刚度随孔隙比减小而增大,阻尼随密度增大而减小;压实度与孔隙比成反比,与密度成正比.被压材料孔隙比减小,压实度增大;密度增大,压实度增大.因此,路面面层压实度随刚度增大而增大,随阻尼减小而增大.
综上分析,振动压路机振动轮垂直加速度与被压材料刚度成正比,与阻尼成反比.被压材料压实度能够较好地反映刚度和阻尼的变化.在振动压实过程中,被压材料压实度的变化反作用于振动轮上.被压材料压实度越大,其反作用力越大,则垂直加速度越大.因此,建立的压实度-振动加速度关系模型能够准确反映被压材料的压实效果.
3 压实度-振动加速度关系模型
以抚吉高速公路试验路段,路面结构层为4cm SBS改性SMA-13上面层+6cm SBS改性AC-20C中面层+7cm AC-25C下面层+8cm ATB-25上基层+16cm水泥稳定碎石上基层+16cm水泥稳定碎石下基层+20cm级配碎石底基层.压实机械为HD130型振动压路机,振动频率为50Hz,振动幅值为0.74mm,行驶速度控制在5km/h左右,激振力为416~528kN.
振动压实实时分析检测系统主要由信号采集、信号处理、信号传输和信号显示与存储4个单元组成.信号采集单元由压电式加速度传感器、温度传感器和GPS信号接收机等组成,负责采集振动轮加速度信号、被压材料温度分布和碾压轨迹.信号处理单元由DH5902动态数据采集仪和Labview虚拟语言程序组成,负责信号放大、过滤、转换和分析.信号传输是基于无线网络通信技术,由路由器、服务器及远程监测PC平台组成,实现振动压实数据远程实时传输.信号显示与存储是接受传输信号,并在电脑、远程监测平台显示压实程度.振动压路机激振信号处理是振动压实度实时分析检测系统的核心,被压材料压实度-振动加速度关系模型是重中之重.振动压实实时分析检测系统结构框架如图4所示.
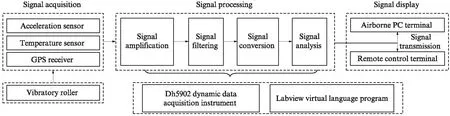
图4 振动压实实时分析检测系统结构框架
3.1 振动加速度信号采集及处理
振动压路机振动加速度信号采集及处理是智能压实技术的第1步.振动轮加速度信号采集及处理系统主要包括DH5902型动态数据采集仪、DH-186型压电式加速度传感器、电脑等.加速度传感器安装方式为磁吸式,分别位于振动钢轮振动轴的垂直方向和45°对称方向3个位置.DH-186加速度传感器参数见表1.
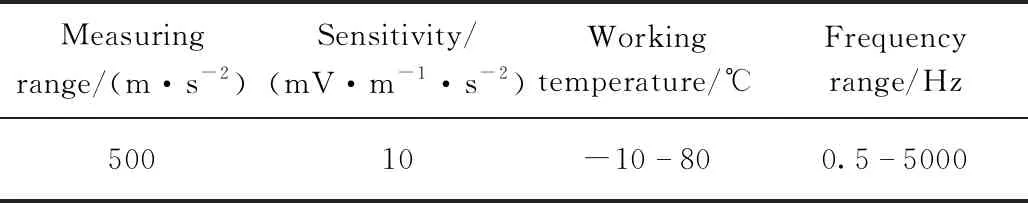
表1 DH-186加速度传感器参数
沥青混合料振动压实信号采集频率通常根据采样信号确定,一般选定采样频率为1000Hz.在振动压实过程中,由于系统内部和周围环境等因素影响,导致在采集信号中夹杂着许多干扰信号.因此,需要对电压信号进行处理,消除或减弱干扰信号,突出有效真实信号,尽可能使加速度信号真实反映振动压实状态.本文选择无限长脉冲响应数字滤波器(IIR)对采集的振动信号进行滤波处理.阻带下边界的截止频率为10Hz,阻带上边界的截止频率为150Hz;带通上边界频率为70Hz,下边界频率为30Hz,通带的平坦度是0.3dB.滤波前,振动信号幅值存在较大差别;滤波后,振动信号幅值基本相等,波形曲线较为光滑平顺,接近正弦波,基本符合振动压路机的振动规律.
3.2 振动加速度有效值选取
以加速度有效值表示1个正弦周期内的加速度值.在沥青混合料压实过程中,一般压路机振动频率f=50Hz,每个振动信号的振动周期为0.02s.考虑到振动压路机行驶速度较慢,振动周期时间短,故需确定反映加速度有效值的振动周期个数,即沥青混合料振动压实连续检测时间.参考文献[17],选取沥青混合料第3遍振动压实第10~22个振动周期的振动加速度数据进行处理分析,结果见表2.
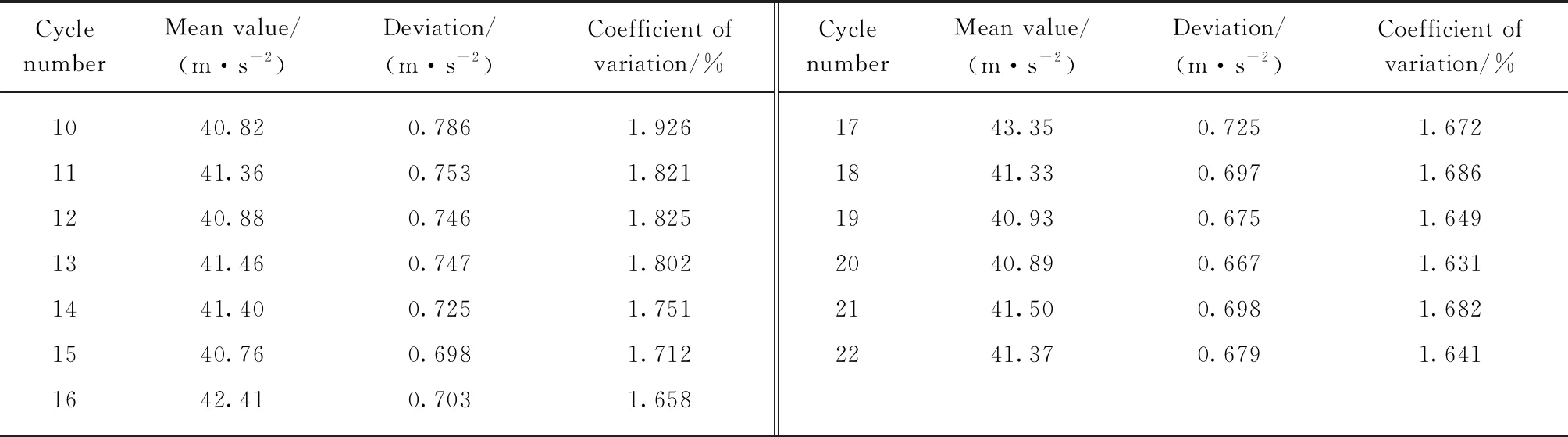
表2 不同周期振动加速度数据处理分析
由表2可见,每个周期数范围内的振动加速度标准偏差均比较小,数据离散性较小,数据比较集中.数据变异系数在第20个振动周期趋于最小值,故采用20个振动周期内的加速度数据进行拟合得到1个有效加速度值是比较合理的.振动信号的采集频率为1000Hz,即相邻2个加速度离散点采集的时间间隔为0.001s,则每个拟合周期(0.02s)采集的加速度离散点数据为20个,推荐振动加速度连续检测分析时间间隔(20周期)为0.4s.
3.3 振动加速度离散性检验与处理
振动加速度采集数据量巨大,难以对全部数据进行分析.本文采用“偏度、峰度检验法”来确定有效数据[18].按检测周期为0.4s,则振动压路机行驶距离约为0.5m.选取24s的压实检测数据,经信号处理后得到60个连续的加速度有效值,结果见图5.
假设H0:数据来自正态总体,n=60.则有
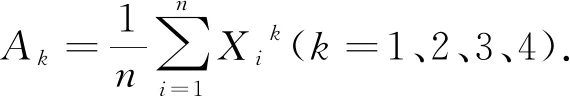
则样本偏度G1和样本峰度G2分别为G1=B3/B23/2=-0.276,G2=B4/B22=2.777.
显著性水平α表示当H0为真时,拒绝H0的概率.zα/4表示标准正态分布的上α/4分位点.当α=0.05时,zα/4=2.244,则H0拒绝域为|μ1|≥zα/4、|μ2|≥zα/4.振动加速度采集样本|μ1|和|μ2|均小于2.244,确定H0成立,判断在同一遍检测的振动加速度数据来自正态分布.因此,该样本数据在置信水平为0.95时,ta/2=2.000,置信区间为(38.72,39.07).置信区间的数据保留,其余剔除.振动加速度采集数据离散性处理结果如图5所示.
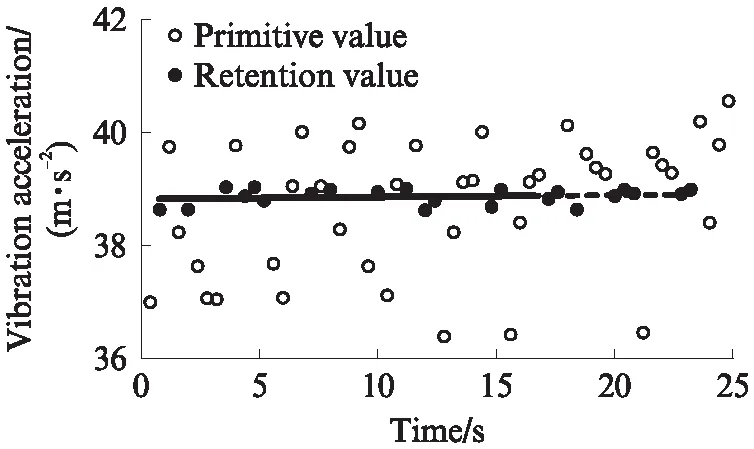
图5 振动加速度离散性处理
3.4 压实度-振动加速度关系模型
依托抚吉高速公路ATB-25基层、AC-25下面层和AC-20中面层试验段,现场采集振动压路机加速度信号,并使用核子密度仪测试压实度.在测试过程中,振动压路机匀速行驶,振幅和振动频率平稳,尽可能保证被压材料受到的激振力恒定.按前述方法对振动加速度信号进行滤波、转换等处理,计算每遍压实后的振动加速度有效值.AC-20、AC-25、ATB-25沥青混合料压实度与振动加速度的关系如图6所示.由图6可见,振动轮加速度与沥青混合料压实度呈线性关系,振动加速度越大,则沥青混合料压实度越大.拟合方程相关性系数R2均不低于0.91,表明拟合效果良好.
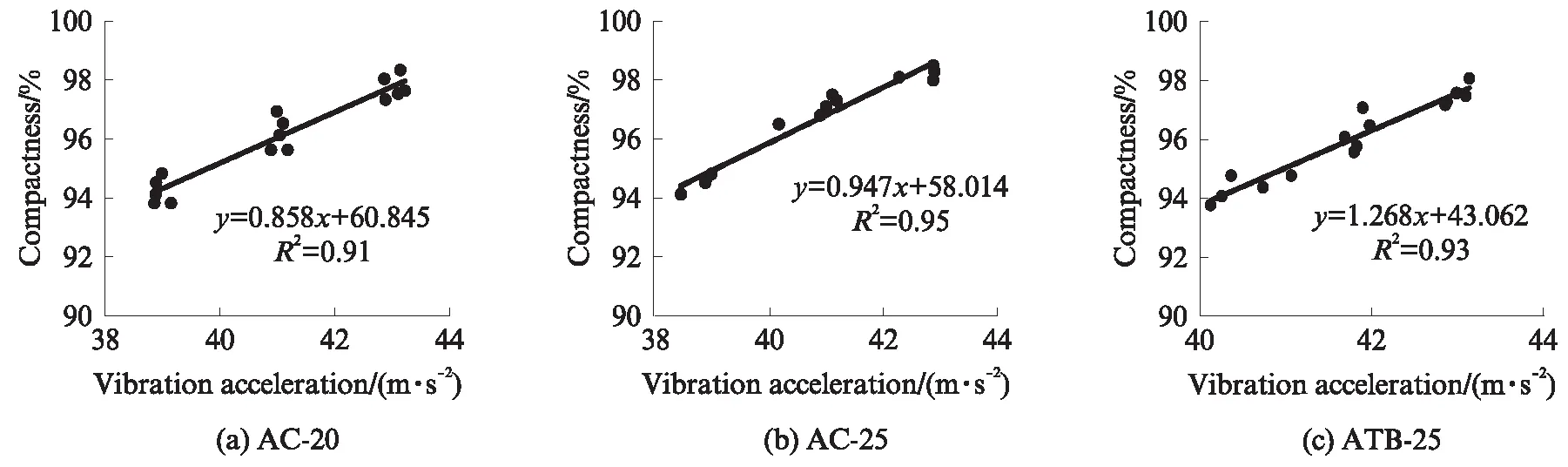
图6 压实度与振动加速度拟合曲线
4 压实度-振动加速度-温度关系模型
在沥青混合料摊铺碾压过程中,温度随时间推移不断下降,其降温规律对混合料智能压实有着重要影响[19].以AC-25沥青混合料为例,开展压实度-振动加速度-温度关系模型研究,以期更加全面反映沥青混合料压实度与振动加速度的关系.
4.1 沥青混合料摊铺-碾压过程温度分布
4.1.1沥青混合料摊铺-碾压过程降温规律
采用红外温度传感器和插入式测温仪测量沥青混合料摊铺-碾压过程中路表温度及距路表4cm处的温度.红外温度传感器选用PT-100型铂电阻温度计,测量范围0~500℃,温度采集探头距沥青混合料高度约25cm.沥青混合料内部温度采用插入式测温仪,以45°角将测温探头插入路面内部.沥青混合料摊铺平面以横向10m、纵向5m范围内为1个测温区域.横向和纵向分别以0.50、0.25m为间隔布置测温点.本文温度采集时风速较小,假定无风,忽略风速对沥青混合料降温速率的影响.施工气温为32~38℃,单向2车道+硬路肩(10.5m)一次摊铺成型,摊铺速度为2.5m/min,双钢轮振动压路机碾压速度4~6km/h,单次碾压长度30m.沥青混合料摊铺-碾压过程降温曲线如图7所示.
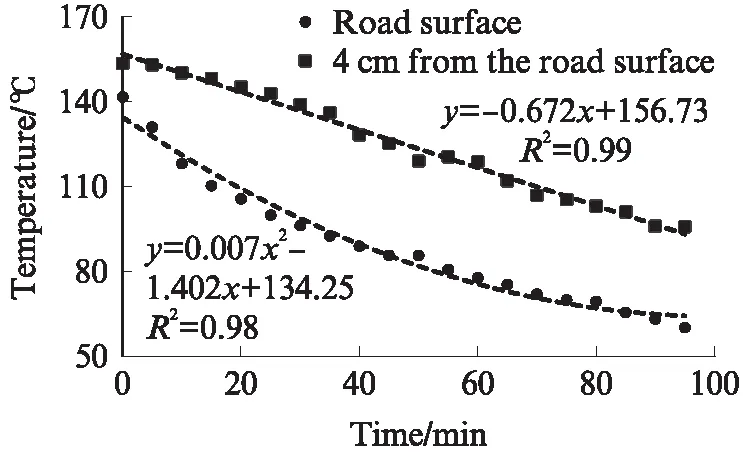
图7 沥青混合料降温曲线
由图7可见:沥青混合料路表温度和路面内部温度散失规律不一致;路表降温呈下凹抛物线,路面内部降温呈线性关系,路表降温速度明显高于路面内部;沥青混合料摊铺后,最初的20min内,路表温度急剧下降,特别是摊铺后5min内,温度能够降低约10℃;距路表4cm处,摊铺后5min内,降温仅1℃ 左右.
4.1.2沥青混合料摊铺横断面温度分布规律
选取3个横断面,每个横断面宽度内测试20个点温度,沥青混合料摊铺横断面温度分布如图8所示.由图8可见,沥青混合料摊铺时,横断面温度曲线中间高,两边低,呈倒V形分布.沥青混合料是由螺旋布料器输送到路面两侧,不断翻转的过程中,温度散失较快.沥青混合料摊铺温度三维曲面如图9所示.由图9可见,沥青混合料摊铺横断面路中间位置的温度比两侧高约10℃,纵断面前后相差约5℃,平均温度变化约1℃/m,温度分布呈波浪状,存在一定的温度离析,碾压均匀性受到一定影响.
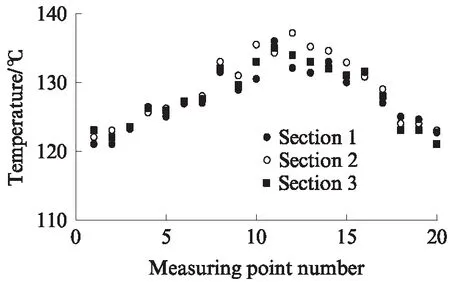
图8 沥青混合料摊铺横断面温度分布
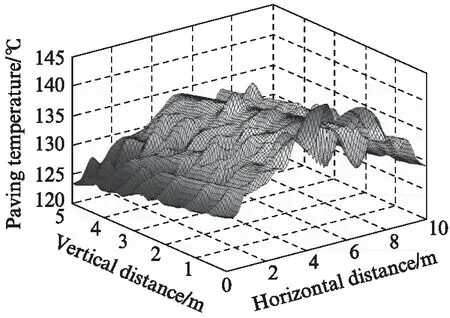
图9 沥青混合料摊铺温度三维曲面
4.2 压实度-振动加速度-温度关系模型标定
碾压温度是沥青混合料压实过程的重要控制参数.本文碾压温度选取125、135、145℃ 3种工况.不同碾压温度下沥青混合料压实度与振动加速度的有效值如图10所示.现场数据采集过程中,测试了3种碾压温度条件下沥青混合料压实度与振动加速度的关系,但在实际碾压过程中,沥青混合料的热量逐渐散失,温度不断下降.因此,有必要构建沥青混合料压实度-振动加速度-温度关系模型:
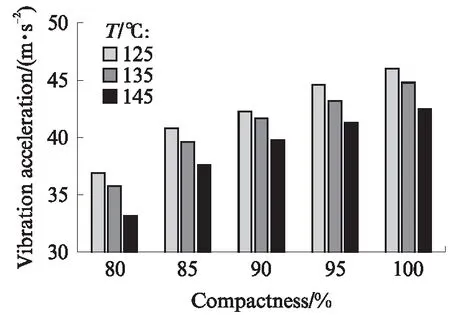
图10 不同碾压温度下沥青混合料压实度与振动加速度有效值
K=aebTα+cT+d
(8)
式中:T为碾压温度,℃;a、b、c、d为拟合参数.
根据图10数据,AC-25沥青混合料压实度-振动加速度-温度关系模型拟合结果如下:
K=0.826e0.009Tα-0.555T+60.934,R2=0.99
(9)
由式(9)可知,AC-25沥青混合料压实度-振动加速度-温度关系模型的相关性系数R2=0.99,拟合效果良好.在125~145℃范围内,沥青混合料温度越高,内摩阻力较小,压实效果越好.以相同功碾压且达到同一压实度时,沥青混合料温度越高,振动加速度测试值越小.碾压温度145℃条件下的振动加速度比135℃条件下、135℃条件下的振动加速度比125℃条件下分别要小约2、1m/s2.温度较低时,其对振动加速度的影响可忽略不计.
4.3 模型计算值与实测值对比
根据式(9)可以得到不同碾压温度时压实度的计算值,实测值为沥青混合料现场摊铺碾压时不同温度采集的压实度值.现场实测值与模型计算值对比结果如图11所示.由图11可见,15个实测点中压实度计算值与实测值相差介于-3.0%~1.4%.综上所述,该模型运用碾压温度和振动加速度实时预测沥青混合料压实度是可行、有效的.
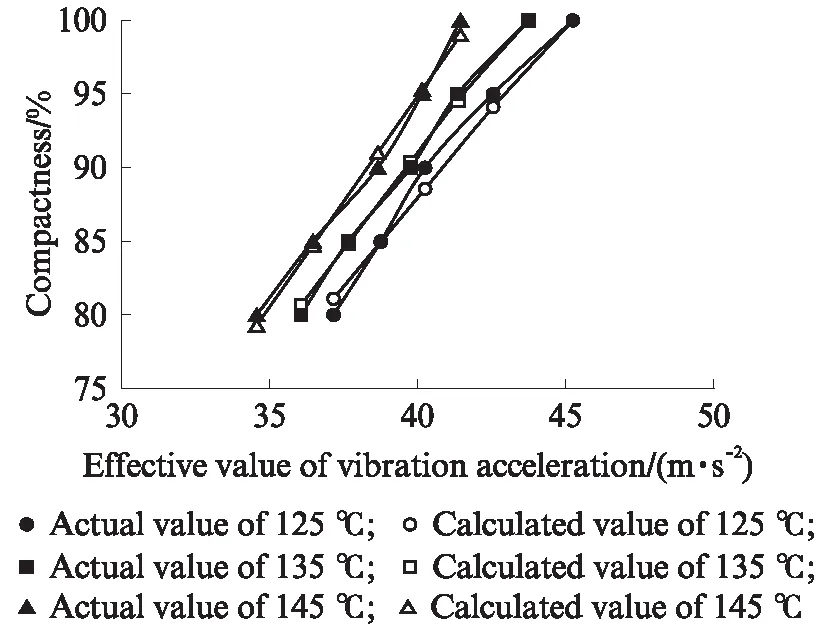
图11 模型计算值与实测值对比
4.4 温度对压实度预估模型影响
选取初始振动加速度为35m/s2,并按0.5m/s2递增,设计17种工况;碾压温度为125、135、145℃ 3种工况,则AC-25沥青混合料压实度-振动加速度模型(CVAM模型)与压实度-振动加速度-温度模型(CVATM模型)对比结果如图12所示.由图12可见:沥青混合料碾压过程可分为3个阶段,压实度- 振动加速度模型随振动加速度有效值逐渐增大分别与压实度-振动加速度-温度模型的高温、中温、低温曲线存在交集;按振动加速度有效值[35,38)m/s2、[38,41)m/s2、[41,43)m/s2分成3级,并与碾压温度125、135、145℃对应,得出CVAM与CVATM压实度计算值相差介于-2.21%~3.04%、-2.39%~1.29%、-1.43%~0.97%.运用压实度-振动加速度-温度模型预测现场沥青混合料压实度是较为科学、合理的.
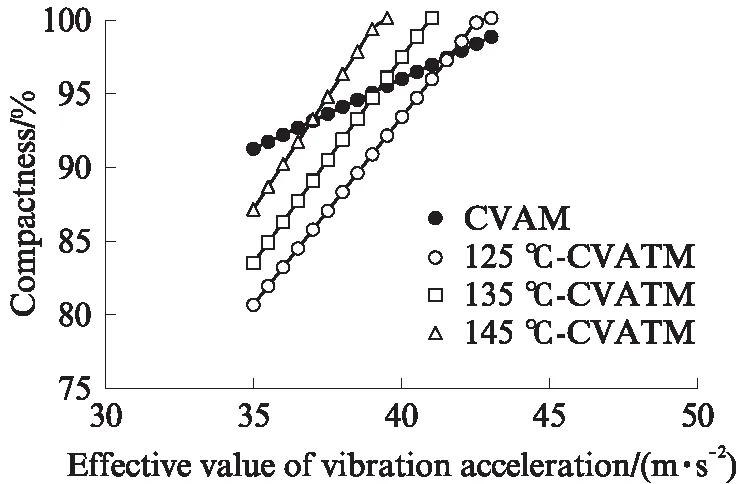
图12 CVAM与CVATM对比
5 结论
(1)振动压路机振动轮垂直加速度与被压沥青材料刚度成正比,与阻尼成反比.
(2)沥青混合料压实度与振动加速度有效值呈线性关系,相关性系数R2均大于0.91.
(3)沥青混合料压实度-振动加速度-温度关系模型相关性系数R2为0.99,压实度计算值与实测值相差介于-3.0%~1.4%.
