基于广义费用函数的多式联运路径优化研究
2021-07-07户佐安贾叶子
户佐安 贾叶子 孙 燕 薛 锋* 赵 宝
(西南交通大学交通运输与物流学院1) 成都 611756) (西南交通大学综合交通大数据应用技术国家工程实验室2) 成都 611756) (大秦铁路股份有限公司科学技术研究所3) 太原 030013)
0 引 言
多式联运参与的主体众多,托运人、承运人及运输管理者等决策主体均出于自身利益考虑对运输组织方案有不同的需求,进而影响多式联运的运输路径和运输方式选择.因此,在多式联运路径优化问题中综合考虑不同决策主体的目标,有利于整合社会资源、提高多式联运效率,实现整个社会综合效益最大化.
国内外学者在多式联运路径优化方面已有诸多研究.Qu等[1]构建了考虑中转成本和碳排放成本的多商品流多式联运整数非线性规划模型;Athanasios等[2]构建了以运输时间最短为目标的模型,并设计相关算法得到最优运输方案;Min等[3]在研究多式联运运输方式选择问题时,以成本、时间和风险为目标,构建了不考虑运输能力限制的优化模型;刘璘等[4]在研究海铁联运路径优化问题时,将总成本划分为制冷成本、运输成本和转运成本,并构建了以总成本最小为目标的冷藏集装箱路径优化模型;李珺等[5]在研究不确定条件下的多式联运路径优化问题时,考虑了运输成本、碳排放成本和时间惩罚成本等因素对运输方案的影响,并构建绿色多式联运路径优化模型;彭勇等[6]在构建模型时,除了考虑运输成本、运输时间等常见因素外,还增加了对运输风险和班期限制的研究;魏航等[7]考虑了危险物品在运输途中可能对运输路线周边人口产生危险,将危险物品途经处的人口覆盖率以及成本、风险共同作为模型目标;甄远迪等[8]在构建不确定情况下的多式联运路径优化模型时,选择的优化目标包括成本、时间、碳排放量及转运节点能力;雷定猷等[9]在研究长大货物多式联运路径优化问题时,在模型构建中增加了适用于长大货物运输的约束条件.
综上,现有关于多式联运路径优化方面的研究较多,但针对于多式联运全过程构建广义费用函数的相关研究较少,且多是从运输客户需求角度,而从交通管理部门出发的研究较少,所考虑的因素不够全面.文中针对当前研究存在的问题,在已有研究成果的基础上,从托运人、承运人和运输管理者等不同决策主体的角度出发,采用广义费用函数体现多式联运对成本、时效性、安全性和环保等多方面的现实要求,构建基于广义费用函数的多式联运路径优化模型,设计算例进行优化,为不同决策主体提供参考意见.
1 多式联运广义费用函数构建
1.1 托运人目标分析
1) 运输成本
(1)
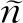
2) 运输时间价值成本 货物运输总时间见式(2),运输时间价值成本优化目标见式(3).
(2)
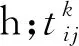
式中:CT为货物运输时间价值成本,元;Vmax为单位集装箱满载时的货物价值,元;η为货物入箱率,%;ρ为年货物持有成本系数,%;Vr为单位集装箱单位时间租赁费用,元/(箱·d).
1.2 承运人目标分析
1) 运输安全性
(4)

2) 运输准时性
minf(tD)=pE·max(ET-tD,0)+
pL·max(tD-LT,0)
(5)
式中:f(tD)为时间偏离惩罚函数;tD为货物到达目的地的时间;pE为货物因提前到达需等待的单位时间滞留成本,元;pL为货物因延迟到达需支付的单位时间惩罚成本,元;ET为客户要求时间窗的最早时间;LT为客户要求时间窗的最晚时间.
3) 运输可靠性
(6)

1.3 运输管理者目标分析
1) 大气污染成本
(7)

2) 噪声污染成本
enk=φ·enuk·ψg·ψp
(8)
式中:enk为我国第k种运输方式的单位噪声污染成本,元/(t·km);enuk为欧洲第k种运输方式的单位噪声污染成本,欧元/(t·km);φ为欧元兑人民币平均汇率;ψg为人均GDP调整系数;ψp为人口密度调整系数.
3) 交通事故成本
(9)

根据该地区该种运输方式的货物周转量,可计算得单位交通事故外部成本,为
(10)
式中:uck为第k种运输方式的单位交通事故外部成本;TCk为第k种运输方式的交通事故总外部成本;TQk为第k种运输方式的总货运周转量.
由上述分析可知,多式联运广义费用函数由运输成本、运输时间成本、运输安全性、运输准时性、运输可靠性和运输外部成本六部分组成,即
s.t.λ1+λ2+λ3+λ4=1,λ1,λ2,λ3,λ4>0
In order to translate Zhuang drama into English and maintain the faithfulness of cultural transmission,understanding the cultural characteristicsof Zhuangdramawill beutmost priority.
(11)
式中:GC为广义费用函数;λi为权重系数,反映各影响因素在广义费用函数中所占比重.
2 模型构建
2.1 问题描述与模型假设
某货主有一批货物需要从起始地O运送到目的地D,货物从起始地到目的地会经过若干个转运节点,每两个相互连通的节点之间可通过铁路、公路、水路三种运输方式进行运输,每种运输方式的运输成本和运输时间不同.每个转运节点处可选择一种运输方式转换,由此产生相应的转运时间和转运成本.在以上条件下,以广义费用函数最小为目标,确定合理的运输方案.
为贴近实际情况并方便对模型求解,提出以下假设:①同一批货物在运输及中转过程中不可拆分;②不考虑不同类别货物间的拼箱运输;③集装箱在运输及中转过程中的箱型均为TEU标准箱;④任意两个相邻节点之间最多只能选择一条路径,每条路径只能选择一种运输方式;⑤不同运输方式的转换只能发生在节点处且每个节点最多只能完成一次中转;⑥不同运输方式的运输能力均能满足托运人货运量的要求.
2.2 模型建立
对相关集合、参数的说明见表1.

表1 模型相关集合、参数说明
以广义费用函数最小为目标,建立模型为
λ3·(pE·max(ET-tD,0)+pL·max(tD-LT,0))+
(12)
s.t.
(13)
(14)
(15)
(16)
(17)
(18)
(19)
2.3 模型求解
本文建立的模型为多目标混合整数规划模型,由于各单目标量纲不同,无法直接采用线性加权法进行求解.理想点法的基本思想是先构造满足所有目标的理想点,之后在约束条件下寻找与该理想点最接近的可行解并以最小偏差量作为目标函数进行求解[10],在多目标决策和多目标优化中已有广泛应用.本文选择该方法进行求解,具体步骤如下.

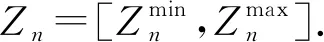


本文采用二项分布赋权法对含有n个目标的多目标模型设定权重,可用概率公式对二项分布描述为
k=0,1,2,…,mp∈(0,1)
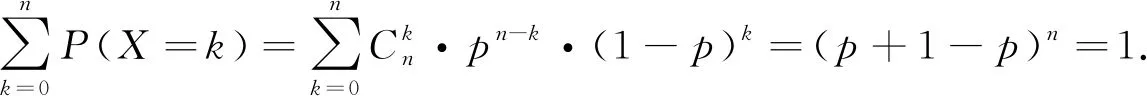
设权重组合为r组,则各组权重对应p=(c+1)/(r+1),其中c可取0,1,2,…,r-1.
通过上述步骤,多目标规划问题转化为以加权欧氏距离最小为目标的单目标规划问题,借助优化求解器LINGO可进行求解.
3 算例分析
3.1 算例描述
某货主现有一批360 t的集装箱货物,采用TEU标准集装箱从起始节点运输到目的节点,假定集装箱满载量为24 t,则所需要标箱数量为15 TEU.运输途中有8个集装箱中转站可进行运输方式转换.

表2 集装箱各运输方式运价核算表

表3 不同运输方式之间单位中转费用 单位:元/TEU

表4 各节点运输距离 单位:km

表5 不同运输方式之间单位节点换装时间 单位:h/TEU

表6 各节点运输方式班期时刻表
铁路运输速度为55 km/h,公路运输速度为65 km/h,水路运输速度为30 km/h.单位集装箱满载运输价值为60万元,货物入箱率为100%,年货物持有成本系数为25%,单位集装箱单位时间租赁费用为100元/(TEU·d).每百公里条件下,公路运输货损率为0.01%,铁路运输为0.015%,水路运输为0.02%,转运节点处货损率为0.04%/次.货物在凌晨零点出发,客户要求的软时间窗为[15 h,25 h],因提前到达需等待的单位时间滞留成本为40元/h,因延迟到达需支付的单位时间惩罚成本为60元/h,运输弧上不同运输方式的各因素可靠度见表7.
大气污染成本计算中,铁路运输以HXD3D型电力机车为例,公路运输以一汽解放J6P重卡为例,水路运输以内河全集装箱船舶相关参数为例,见表8~14.铁路运输中,假定电力机车能源结构中77.7%来源于火力发电,平均传输损耗率为93%,充电损耗率为20%,燃烧1 t标准煤生产的可用电量为8 131 kW·h.

表7 运输弧上不同运输方式的各因素可靠度

表8 HXD3D型电力机车相关参数表

表9 标准煤排放率 单位:kg/t

表10 一汽解放J6P重卡相关参数表

表11 公路运输污染物功率排放表 单位:g/(kW·h)

表12 内河全集装箱船舶相关参数表

表13 水路运输污染物功率排放表 单位:g/(kW·h)

表14 污染物排放单价表 单位:元/kg
欧元兑人民币平均汇率为7.783 4(2019年),人均GDP调整系数为0.26,人口密度调整系数为1.19,欧洲噪声污染情况见表15.

表15 欧洲噪声总成本和平均单位噪声成本预测值
根据我国实际情况,事故死亡1人平均赔付30万元,受伤1人平均赔付5万元,公路事故管理救助成本为1 000元/起,铁路事故为10万元/起,水路事故为15万元/起.通过查阅相关统计年鉴和行业数据,得到不同运输方式2018年的交通事故统计情况和货运周转量,见表16.
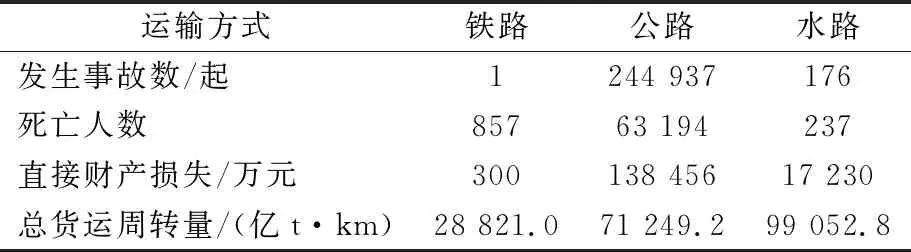
表16 各运输方式交通事故相关数据
3.2 算例求解
采用二项分布赋权法对六个目标设定权重,设权重组合为10组,得到各组权重对应p=(1/11,2/11,…,9/11,10/11).借助数学规划软件LINGO12.0对不同权重组合下的单目标规划模型进行求解,得到多组最优解下的多式联运运输方案,见表17.

表17 不同权重组合下的运输方案
由表17可知,当p=1/11时,运输外部成本目标权重取最大,运输方案为铁水联运,可见公路运输所产生的外部成本远大于铁路和水路运输,从运输管理者角度制定运输方案时,为降低运输外部成本,应尽量选择铁水联运模式;当p从2/11增加至6/11时,运输外部成本目标权重逐步减小,而承运人所关注的安全性、准时性和可靠性的目标权重逐步增大,此阶段运输方案为公铁联运且铁路运输所占比例远大于公路运输,说明公铁联运在时效性方面强于铁水联运,而铁路运输的安全性、可靠性等指标优于公路运输和水路运输,因此从承运人角度制定运输方案时,应优先选择铁路运输和其他运输方式组合的运输模式;当p从7/11增加至10/11时,托运人所关注的运输成本和运输时间价值成本的目标权重不断增加,而承运人和运输管理者的目标权重都有所减小,此阶段运输方案经历了由公铁联运转为全程公路运输后又转为公铁联运的过程,且公路运输与铁路运输所占比例相近,可看出公铁联运模式可同时满足时效性和成本两方面要求,因此从托运人角度制定运输方案时,从时效性和成本两方面考虑时应尽量选择公铁联运.
4 结 束 语
本文考虑了多式联运不同决策主体的需求,分别对其目标进行分析和量化处理,建立了包含运输费用、运输时间价值成本、时间偏离惩罚成本、运输外部成本、运输安全性和运输可靠性在内的多式联运广义费用函数,并以广义费用函数最优为目标构建了多式联运路径优化模型.设计理想点法并应用LINGO12.0对算例进行求解,获得了不同权重组合下的多组全局最优解,算例求解结果表明本文所建模型能够为不同决策主体提供参考依据,同时能够较好平衡不同决策主体目标之间的关系,具有一定的有效性和实用性.为简化模型,本文对多式联运外部成本的核算方法进行了部分简化,这也是后续将进行的工作.
