扭曲型材腹板曲面几何模型研究
2021-07-07王全华李培勇张文杰
王全华 李培勇 吕 浩 张文杰
(武汉理工大学产业集团有限公司1) 武汉 430063) (武汉易华船舶设计有限公司2) 武汉 430063) (武汉理工大学交通学院3) 武汉 430063)
0 引 言
船舶上数量众多的型材构件是支撑船体外板、保证船舶形状和承受载荷的重要结构件,而且在腹板平面内具有弯曲形状,还有少量的具有扭曲形状,甚至是既弯又扭的弯扭构件.扭曲结构件主要分布在船艏或艉区域内.扭曲状型材构件的出现,在结构形式上保证型材腹板与船体外板呈正交关系,使船体结构具有更大的承载能力,而且正交结构有利于型材构件和船体板的装配,避免腹板与外板之间出现较小的装配角度,影响装配.
扭曲型材构件在舰船上使用较多,加工工艺复杂,缺乏专用加工设备,生产中一般通过人工操作压力机借助特殊工装完成.这种工作方式依赖于人工经验,效率低,成本高,质量不够稳定,因此,企业迫切希望研制出用于扭曲型材加工的自动化设备.为了实现这一目标,需要做很多工作,其中重要的一项是掌握扭曲型材的几何特点.
弯扭构件常见的形式是箱形截面空间弯扭构件[1],例如,中国国家体育馆的钢结构[2].不过,船舶扭曲构件和上述箱形截面空间弯扭构件的设计方法、几何形状表达方式等方面存在较大的差异.迄今,尚未看到相关的文献资料.因此,需要针对船舶弯扭构件的几何问题进行专项研究.
常用的船舶型材包括T型材、角钢和球扁钢等薄壁材料,其中角钢和T型材由腹板和面板组成,球扁钢则包括球头和腹板.型材扭曲加工过程中,面板(或球头)和腹板一起变形.根据装配的要求,加工时一般以腹板曲面形状符合设计要求作为加工目标,对面板形状则不做专门要求.并且,由于薄壁型材腹板的厚度远小于其平面尺寸,所以可忽略其厚度的影响.
文中以扭曲型材腹板曲面的几何特征作为主要研究内容,分析了扭曲型材构件的截面特征,采用双三次B样条对腹板曲面进行几何建模,从理论上证明了扭曲型材构件腹板曲面的任意横剖线都是直线[3],其腹板曲面具有直纹面特征,可以采用直纹面进行建模.
1 扭曲型材几何特征分析
不考虑型材的板厚,在整数肋位剖切扭曲型材,见图1.其剖面线具有以下特征:①腹板和面板剖线均属于直线,长度分别为腹板高度和面板宽度;②面板剖线与腹板剖线垂直,腹板剖线与肋骨型线垂直.

图1 扭曲型材剖面图
分析扭曲纵向构件在不同肋位处的腹板剖线,可看出属于异面直线.分别顺次连接整数肋位腹板剖线上相应的两个端点,得到型材构件的外口线和内口线,见图2.其中外口线即型材与船体外板的装配线.船舶设计时,通常只定义外口线与肋骨剖面交点的坐标,放样时再确定内口线.

图2 腹板的外口线和内口线
2 B样条曲线曲面
B样条曲面是张量积曲面,它是由两个方向上的控制点网格、两个节点矢量和单变量B样条基函数的乘积定义的,其曲面方程为[4-6]
(1)
式中:Pi,j(i=0,1,…,n;j=0,1,…,m)为(1+n)×(1+m)的控制点阵列;Ni,p(u)为定义在节点矢量U上的p次B样条基函数;Nj,p(v)为定义在节点矢量V上的q次B样条基函数.节点矢量U和V为
(s=n+p+1)
(t=m+q+1)
B样条曲面的反算是指已知一组矩形阵列的数据点,求解一个通过所有数据点的B样条曲面.反算过程分为节点矢量的确定和控制点的计算,控制点的计算也可以转化为两步B样条曲线控制点的计算.
3 扭曲型材构件腹板曲面的拟合
为了方便叙述,将坐标系统一为船体坐标系,即X方向为船长方向,船艏为正;Y方向为船宽方向,右舷为正;Z方向为型深方向,向上为正.将腹板剖线与水线面的夹角定义为扭曲角θ,见图3.

图3 扭曲角的定义
船舶设计时,通常只定义外口线与肋骨剖线交点Q的坐标,放样时再确定内口上线对应的点Q′的坐标值.
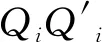
(2)
因此对于扭曲型材的腹板,已知的数据点只有腹板外口线和内口线上的两组数据点,见图4中实心圆.

图4 已知的数据点以及数据点的加密
欲用双三次B样条拟合腹板曲面,仅有两组数据点不够,需要对数据点加密.根据扭曲型材的剖面特征可知,其腹板在整数肋位处的剖线是直线,因此可在同一肋位上外口线和外口线上两数据点之间做线性插值,生成n等分点,见图5中空心圆.
对每一肋位的数据点都按同样方式加密,最终得到(1+n)×(1+m)个数据点,记为Qi,j(i=0,1,…n;j=0,1,…,m),上述数据点中的任意一列数据点均为对应腹板剖线上的n等分点,因此对任何一列数据点,均存在以下关系:
(i=0,1,…n;j=0,1,…,m)
(3)
根据B样条曲面的反算方法可知,腹板曲面控制点的反算分两步:
步骤1拟合通过每列(1+n)个数据点的曲线,也就是腹板剖线,得到(1+m)组控制多边形,每组控制多边形含有(3+n)个控制点,记第一步反算得到的控制点为{Ri,j}(i=0,1,…,n+2;j=0,1,…,m);
步骤2将第一步反算得到的控制点作为新的数据点,拟合通过每一组新数据点的曲线,得到(3+n)组控制多边形,每组控制多边形含有(3+m)个控制点,记最终的控制点为Pi,j(i=0,1,…,n+2;j=0,1,…,m+2).
下面以某35 000 DWT散货船的舷侧纵桁为例进行说明.该船从船艉FR12到FR20在4 500 mm吃水处设有一扭曲纵桁,见图5.采用图5所述的方法在外口线和内口线之间做线性插值,生成n等分点.经过两步反算得到控制点阵Pi,j(i=0,1,…,7;j=0,1,…,10)和腹板曲面.连接控制点得到8×11控制网格,最终拟合得到的腹板曲面见图6.
蕲州城中有一小河,初为小溪,碧流如玉,两岸杨柳依依,故名小柳河。流至荆王府水面渐宽,名为二郎河,注入长江成一道绿,如青龙戏水,直入云天。相传吴承恩在荆王府中创作不朽名著《西游记》,每至疲惫困惑之时,便到河边漫步,河风一吹,顿觉神清气爽,灵感天降,有如二郎神君相助,故赐名二郎河。明亡清兴,二郎河悄然易道,渐次消失,仅存上游小柳河溪水叮咚,清澈如故。
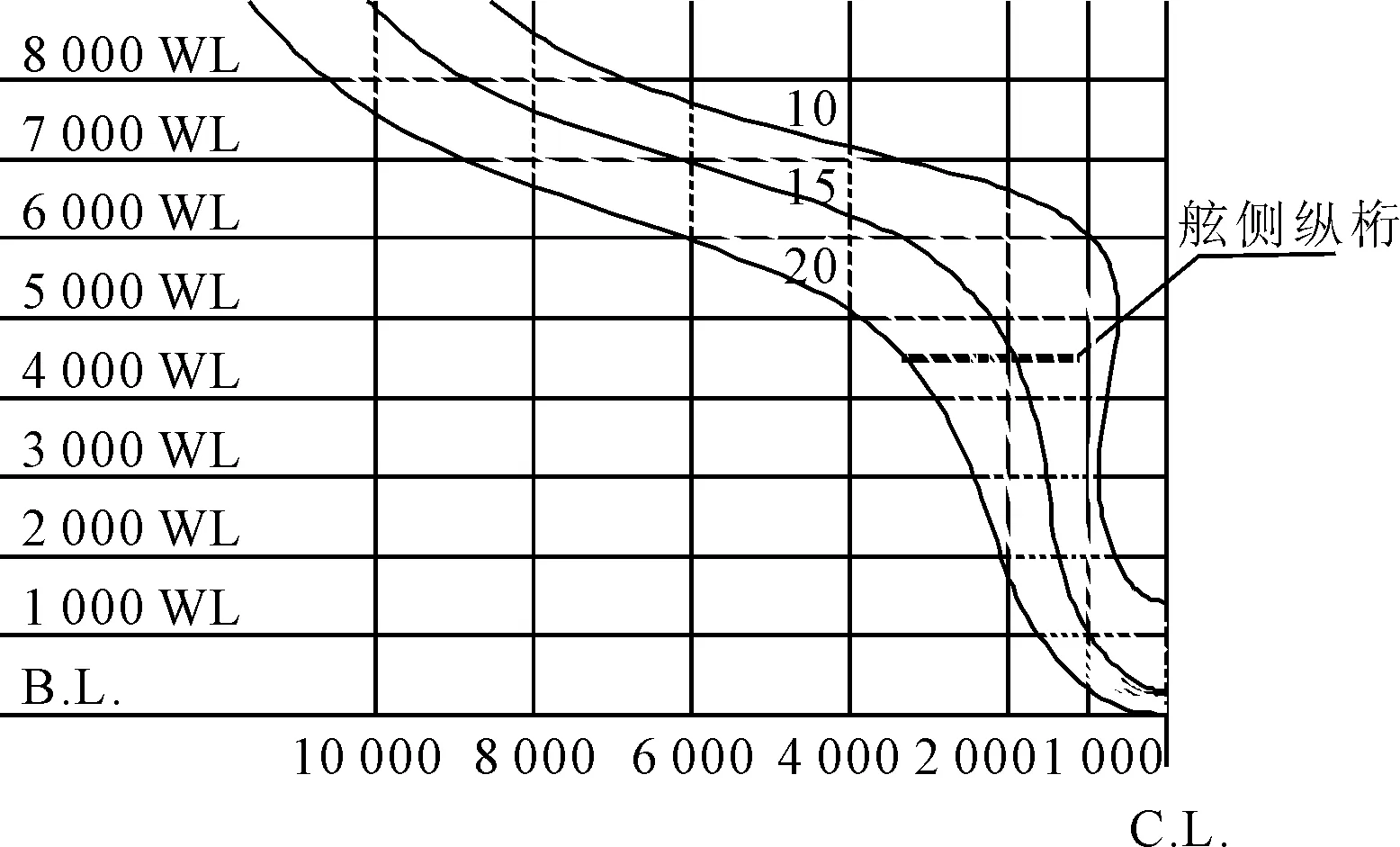
图5 局部肋骨型线图和舷侧纵桁

图6 拟合的腹板曲面
采用上述曲面方程,对腹板曲面进行插值,其中半肋位横剖面(如10.5、11.5、…、17.5)与扭曲构件腹板曲面的交线见图7.

图7 中间肋位剖线
由图7可知,半肋位腹板剖线都是直线,并且控制线上控制点的分布程度相同.随机选择了一些横剖面进行计算,计算结果具有相同的特点,因此初步认为腹板曲面在任意横剖面处的剖线都是直线.
4 腹板曲面任意横剖线都是直线的证明
4.1 证明控制线都是直线且控制点分布均匀程度相同
对于第一步反算的控制点,由于加密后的每一列数据点Qi,j都是在原始的外口线和内口线相应数据点之间通过线性插值生成的n等分点,因此经过第一步反算得到的控制点Ri,j(i=0,1,…,n+2;j=0,1,…,m)中的每一组控制点也是线性分布的,且分布均匀程度相同,即:
Ri,j=(1-ki)R0,j+kiRn+2,j
(i=0,1,…,n+2;j=0,1,…,m)
(4)
由式(4)可知:
(i=0,1,…,n+2)
(5)
即上述控制点中的任意一行控制点都是第一组控制点和最后一组控制点的线性组合.
(6)
式中:
因为
Ri,j=(1-ki)R0,j+kiRn+2,j(i=0,1,…,n+2)
所以
(7)
即:
Pi,j=(1-ki)P0,j+kiPn+2,j
(i=0,1,…,n+2;j=0,1,…,m+2)
(8)
故每一个横剖面上的一组控制点都是线性分布的,且分布情况相同,连接每一组控制点得到的控制线也都是直线.
4.2 证明腹板曲面任意横剖线都是直线
根据B样条曲面的正算算法有:
(9)
由B样条基函数的规范性可知:

(10)
在v=vt的等参数曲线上取S(u1,vt)、S(u2,vt)和S(u2,vt)三点.
(11)
(12)
(13)
因为
所以
S(u1,vt)-S(u2,vt)∥S(u2,vt)-S(u3,vt)
故在v=vt的等参数曲线上,S(u1,vt)、S(u2,vt)和S(u2,vt)三点共线,命题得证.
扭曲型材构件腹板曲面的任意横剖线都是直线的特征,对于扭曲加工过程中成形控制非常有意义,例如,腹板任意横剖线对应的扭曲角可以很方便的用于成形检测.
5 直纹面方程表达扭曲型材腹板曲面
扭曲型材腹板曲面在任意位置处的横剖线都是长度为腹板高度的定长直线,在数学上,具备这种特征的曲面称为直纹面.
对直纹面而言,当素线相互平行或相交时,形成的直纹面属于单曲面(如圆柱面和锥面),否则称为扭曲面(如螺旋面和双曲抛物面).船体扭曲型材腹板曲面是由腹板剖线沿着内口线和外口线运动形成的,由于不同肋位的腹板剖线属于异面直线,既不平行也不相交,因此腹板曲面属于扭曲面.
工程上,直纹面一般表达为
S(u,v)=(1-v)a(u)+vc(u)
(16)
即直纹面本质上就是表达直纹面的两条边界导线.对于扭曲型材的腹板曲面,母线是其腹板剖线,边界导线是其外口线和内口线,拟合腹板曲面实际上就是拟合腹板曲面的内口线和外口线.若用3次B样条方法拟合内口线和外口线,那么得到的腹板曲面实际上就是3×1次B样条曲面.
以上文的扭曲纵桁腹板为例,采用三次B样条拟合外口线和内口线,最终拟合的腹板曲面见图8.

图8 腹板曲面
为了了解B-样条曲面和直纹面方程在拟合扭曲构件腹板曲面的差异,分别采用两种方法进行插值.不失一般性,在半肋位剖面线上进行插值计算点,两种方法的插值结果显示,分别采用双三次B样条方法和直纹面方程分别拟合扭曲型材腹板曲面(取自由端边界条件),对应插值点的偏差均不超过0.01 mm,这种偏差在工程上可以忽略不计.但是比较两种拟合方法的计算过程和计算量,显然用直纹面拟合扭曲型材腹板曲面,过程更简单,计算量更小,因此采用直纹面方程拟合扭曲型材的腹板曲面更为便捷.
6 结 论
1) 分析了扭曲型材构件的几何特征,根据设计和制造的特点,将腹板曲面作为主要的研究对象.
2) 采用B样条曲面对型材腹板曲面进行建模,模型结果显示腹板曲面在任意横剖面上的剖面线都是直线,并从理论上对此结论得以证明.
3) 扭曲型材腹板曲面具有直纹面的特征,可以采用直纹面方程进行建模,并以具体算例验证了结论的正确性.
