激波管内黏性流场流动数值模拟
2021-07-07汪东旭张尊华梁俊杰衡怡君李格升
汪东旭 张尊华 梁俊杰 衡怡君 李格升
(武汉理工大学能源与动力工程学院 武汉 430063)
0 引 言
激波管是一种利用激波实现对工质进行加热获得目标范围内温度和压力的实验装置[1-2],其包括两端封闭的圆管和膜片分隔开的驱动段和被驱动段.激波管有结构简单,可在较宽范围调节试验区的温度和压力的优点,广泛应用于研究可压缩流体现象、高温气体、气相燃烧反应和超音速燃烧等领域.
随着国内外流体数值模拟软件的发展,计算流体力学(CFD)数值计算技术在激波与介质相互作用机理研究中占据较为重要的地位,可应用计算流体动力学流场可视化方式研究和解释激波管内的流场结构[3].激波管在设计优化前,需预先了解激波管中的流动和激波运行过程,由于数值模拟可以在较广的参数范围内较快给出定量效果,所以可在设计初期利用数值模拟来优化激波管性能参数,选择最佳结构和驱动方案;使用CFD数值模拟方法可设置多测点监测激波的传播及参数变化曲线,能够直观预测激波运行过程中内部气流之间、流体与管壁之间和流动随时间变化过程中气体间的相互作用而产生的热力学特性,获得空气动力参数,如温度、压力、密度等参数分布;利用数值方法对激波管内流场流动进行计算对实际设备的传感器测量过程也有参考意义.
近年来,国内外学者针对激波管内激波和流体运动特性进行了一系列试验与模拟研究,无黏模型和层流黏性模型在激波管的流动数值计算中得到广泛应用.Lamnaouer等[4]针对高压激波管,模拟了激波在非反应流和反应流中的传播和反射,对激波管侧壁传热和反射激波/边界层相互作用等非理想状态进行了量化研究,模型能够准确地模拟激波和膨胀波的传播和反射以及激波反射后的流动不均匀性;Amrollah等[5]在两种不同驱动气体压力和膜片厚度的情况下,基于激波管二维轴对称模型研究了正激波在层流粘性流体中的运行过程,仿真激波通过的时间间隔数据与试验数据一致性良好;Davidson等[6]利用激光诊断技术对激波管边界层效应进行了试验研究,结果表明:边界层与激波分岔发生在湍流区域,它们受激波管结构和激波前后条件影响;何中伟等[7]通过试验研究发现实际激波管中管壁壁面边界层基本上是湍流边界层占主导,激波与边界层干扰中,大多是激波与湍流边界层的相互干扰.为更准确反映激波管中的物理现象,有必要对激波管进行湍流流动模拟研究并验证其结果的可信度,其结果可为下一步开展激波管流体力学与化学动力学耦合的参数化研究提供重要理论依据.
利用数值模拟的方法,模拟理想气体空气在总长为2.08 m、直径为67.00 mm的激波管内湍流粘性流场的流动过程,并与相关试验数据进行对比,验证模拟方法的可靠性.依据不同时刻下激波传播位移和入射激波后温度、压力等参数随时间的变化,总结激波运行规律,获得激波管最大试验时间限度.
1 数值模拟方法和边界条件
1.1 几何模型描述
研究对象为轴对称结构激波管,采用二维模型对计算区域进行建模,见图1.该模型参考了阿米尔卡比尔理工大学的小尺寸激波管全几何形状,激波管长度为2.08 m,直径为67.00 mm,主要由高压段、中间膜片、低压段三个部分组成,破膜方式为压差破膜,当高压段和低压段达到一定压差时膜片破裂产生激波.

图1 激波管计算区域
X=0处定义为膜片位置,高压驱动段长度为0.64 m,低压被驱动段长度为1.44 m,为记录不同位置的流体压力随时间的变化,在高压段靠近膜片处至低压段尾端依次分别设置了9个压力传感器监测点Sn,监测点位置见表1.
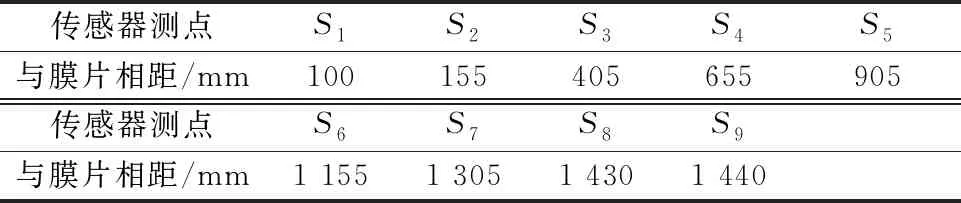
表1 监测点位置
1.2 控制方程
为描述激波管内的流体流动,采用非定常雷诺平均纳维-斯托克斯方程进行数学建模.其流体力学控制方程包括连续性方程、动量方程和能量方程,为
连续方程:
(1)
动量方程:
(2)
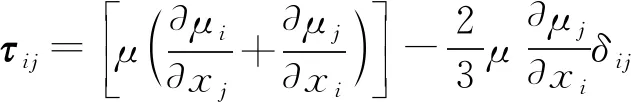
能量方程:
(3)
式中:keff为有效热传导系数;Jj为组分j的扩散流量;Sh为其他体积热源项,不考虑化学反应的情况下,Sh=0,以上方程右边的前三项分别表示热传导、组分扩散和黏性耗散引起的能量运输.
控制方程通过有限体积法转换为可以用数值方法求解的代数方程,在每个控制体内积分控制方程,进而产生基于控制体的每一个变量都守恒的离散方程.对与任意控制体积V的积分形式的方程有:
(4)
式中:ρ为密度;v为速度矢量;A为曲面面积矢量;Γφφ为φ的扩散系数;φ为φ的梯度,对二维问题即为(∂φ/∂x)i+(∂φ/∂y)j;Sφ为单位体积φ的源项.对于每个网格区域:
(5)
式中:Nfaces为封闭单元面的数量;φf为通过表面f的对流量;ρfvf·Af为通过表面的质量流量;Af为表面f的面积;φf为表面f上φ的梯度;V为单元体积.
1.3 模型模拟方法的选择
湍流是一种高度复杂的三维非稳态、带旋转的不规则流体运动[8].超声速流动模拟中常用的有Baldwin-Lomax代数涡黏性模型,Spalart-Allmaras湍流模型,k-ε双方程模型,为仿真激波管内多尺度复杂流动的激波及非定常流场流动,选用模拟复杂流动和高压力梯度流动均有较好性能的双方程湍流模型,该模型用于计算有旋的均匀剪切流,平面混合流,平面射流,圆形射流,管道内充分发展流动,都取得了与实验数据比较一致的结果[9].压力基求解器主要适用于低速不可压缩流体,故采用适用于高速可压缩流体的密度基隐式求解器.求解器的时间类型设定为瞬态,Flux-Type选择Roe-FDS差分格式,Roe格式可在流动不连续性附近产生振荡解,标量梯度采用基于格林高斯网格节点方法,空间离散化采用二阶迎风格式,为提高计算精度,选择双精度并行模式进行数值模拟.在求解初始化过程中,利用patch命令对高低压区分别设置相应的初始压力和温度,仿真迭代时间步长为1×10-7s,最大迭代次数为20.
1.4 网格划分和网格敏感性验证
运用前处理软件ICEM划分网格,为了加速计算收敛,采用良好的结构化四边形网格对计算区域进行离散化,在壁面附近创建精细的网格层以捕捉边界层效应,局部计算网格见图2.
图2 局部计算网格
FLUENT软件数值模拟结果与网格划分质量有很强的关联性,为减少数值误差对模拟结果的影响,进行了网格敏感性研究.在长为2.08 m、直径为67 mm的模型中,绘制网格数目分别为700×15,1 000×20,2 000×25,2 500×40和2 999×80的五种计算网格,X轴方向基础网格尺寸分别约为2.971,2.080,1.040,0.832和0.694 mm,Y方向全局加密比例因子设置为1.111,以上网格正交质量接近1,网格最大长宽比均低于边界值80,处于理想范围内[10].选用相同的边界条件(air-air,p4=500 kPa,p1=50 kPa,T4,1=300 K)和数值方法进行数值模拟,记录t=1.0 ms时刻激波管径向Y=0.03 m位置所对应的3区和2区接触面处温度边界层内等值线轴向坐标值,见图3.由图3可知:发现随着网格数增大,径向Y=0.03 m位置所对应的等温线轴向坐标值差异越小,当网格数增大到2 000×25时,激波管温度边界层内温度分布几乎不受网格变化影响,综合考虑计算成本和求解精确性等方面,选择网格数为2 500×40(X轴方向基础网格尺寸为0.832 mm)的网格划分方案开展二维激波管内流体流动数值模拟研究.
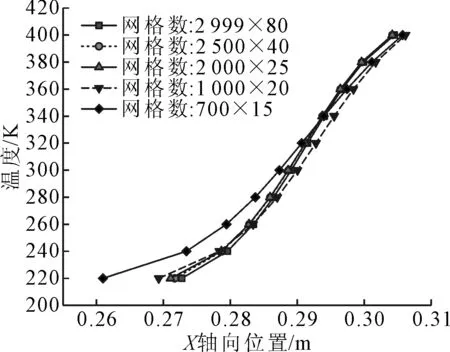
图3 径向Y=0.03 m时,激波管内温度等值线轴向坐标分布
实际激波管中可观测到湍流和层流两种边界层,层流边界层向湍流边界层转变是通过临界雷诺数定义的,层流边界层只有在被驱动段初始压力很低、激波较弱等条件下可能存在,边界层大部分区域是湍流的.y+值为管壁有界流动的无量纲壁面距离,是评判各种模型壁面边界层网格分辨率的一个重要参数[11].采用标准壁面函数划分湍流边界层网格,合理的y+值应在(30,300)范围内,以保证流场结构解析到粘性子层,壁面边界层网格y+值计算公式为
(6)
式中:Δy为第一层网格与壁面之间的距离;ρ为流体密度;UT为流体速度;μ为黏性系数,随着网格分辨率的增加,y+值会减小,利用这种规律使网格分辨率达到理想值.通过调整管壁第一层网格高度后经计算获得.由于本文流场是瞬态流动,需利用不同时刻壁面边界层y+值判断边界层网格设置质量,值设定为0.05 mm时,记录Case1激波运行全过程壁面边界层y+值,不同时刻壁面边界层y+值均在(30,36)范围内,故认为本文湍流边界层网格设置是合理的,第一层网格与壁面之间的距离值设置为5×10-5.
1.5 初始边界条件
由图2可知,模型共有壁面(wall)、轴对称(axis-symmetry)、内部面(interior)三种边界类型,忽略浮力和重力影响:①激波管左右两端端壁和两侧管壁均设定为绝热、无滑移wall边界;②管体设定为axis-symmetry边界;③膜片部分设定为interior边界.
数值模拟初始条件见表2.本文研究背景为无反应流场流动,为避免非理想介质对模拟结果精确性的影响,高低压段气体工质均设定为理想空气,黏性常数为1.789 4×10-5kg/(m·s).基于以下边界条件,研究激波的传播规律,分析激波运行和激波后温度边界层的分布规律.
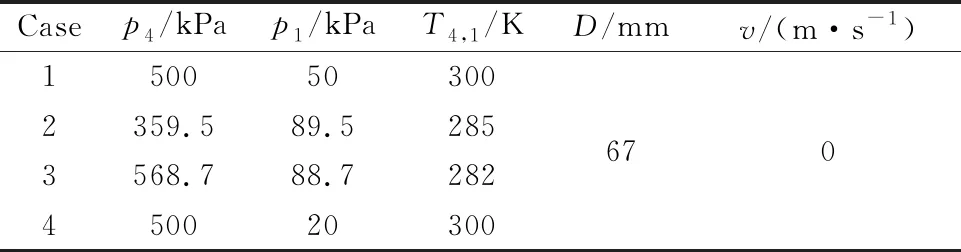
表2 数值模拟的边界条件
2 数值模拟方法的验证
为验证湍流粘性流体数值模拟方法的适用性,需将数值计算得到的结果与实验数据进行对照分析,文献[5]中激波管几何模型与本文相同,实验设定的边界条件见表3.本文激波管湍流模型采用相同的实验条件进行模拟计算,湍流模拟算例记为Case2和Case3,激波位移计算结果情况见图4.

表3 文献实验条件
图4 不同工况下入射激波所抵达的位置
由图4可知,Case2条件下,t=0.002 2 s时,正激波抵达位置的横轴坐标为X1=0.966 m,入射激波速度为vs=452.73 m/s;Case3条件下,t=0.002 0 s时,正激波抵达位置的横轴坐标为X2=0.991 m,入射激波速度为vs=495.5 m/s.
将湍流模拟不同时刻入射激波速度与文献数据进行对比,见表4.由表4可知,本文湍流数值模拟算例2在0.002 2 s时刻得到的激波速度相对文献试验数据的误差为0.291%;算例3在0.002 0 s时刻激波速度相对试验数据的误差为2.641%.数值模拟结果与试验结果存在一定的误差,考虑到试验过程中激波管管壁为非绝热壁面,同时实际流体的黏性效应和激波管壁面的摩擦效应会使激波强度有一定的损失,而模拟时假定激波管管壁为绝热恒温无滑移壁面,因此模拟结果与试验结果必然会产生一定的误差.湍流模拟结果相对于层流模拟更接近试验数据,且两个算例模拟结果产生的误差数值小于5%,均在数值模拟误差可接受范围内,综上所述,可认为该湍流粘性流体数值模拟方法适合用于预测激波管内激波的运动特性.

表4 湍流模拟结果与文献试验、模拟值对比
3 模拟结果与讨论
3.1 激波的产生与传播
在仿真初始状态,高低压段充入不同压力的空气,此时管内包含两个区域:初始高压气体区域(4区)、初始低压气体区域(1区).模拟过程从膜片破裂时刻(t=0 s)开始,假设X=0 m处的膜片瞬时破裂消失,见图5.由图5可知,初始时刻,4区与1区之间的压力间断面称为接触面.

图5 t=0 s时刻,膜片破裂时激波管内瞬时压力(Pa)云图(Case4:p4=500 kPa,p1=20 kPa,T4,1=300 K)
高低压气体之间的压差会使气体进行非定常运动,同时形成正激波向低压段传播,入射激波和反射激波对工质进行压缩加热加压,由于激波对介质的加热时间极短,可认为整个压缩加热过程是绝热、非等熵、均匀加热的.图6为t=1.50 ms时刻沿轴向位置管内入射激波后管体温度局部分布云图.由图6可知:入射激波压缩区域温度高于初始温度,膨胀波压缩区域温度低于初始温度,其中具有温度梯度的薄层称为温度边界层[12].壁面边界层温度高于中心主流区温度,这是由于粘性影响,气体在边界层内减速,动能转化成热能,边界层内的流动为非等熵过程,同时存在动能交换和热交换过程,因此温度边界层处的温度要高于中心主气流.
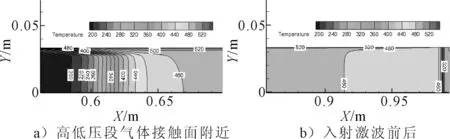
图6 t=1.50 ms时,沿轴向位置管内温度(K)局部分布(Case4:p4=500 kPa,p1=20 kPa,T4,1=300 K)
此时,激波管内形成四个区域,沿轴向位置温度分布见图7,膜片破裂后,产生的正激波由膜片位置向低压段传播,正激波与高低压段气体接触面之间的区域称为2区,产生的膨胀波向高压段传播,膨胀波与接触面之间的区域称为3区;正激波到达右侧尾端端壁后会发生反射产生反射激波,反射激波经过的区域称为5区,即试验区.粘性流体流经管体壁面时,入射激波后壁面附近的流体区域会形成一定厚度的边界层,边界层内激波速度会迅速降低,在管壁处的速度为零,激波管内2区、3区及5区壁面因流体粘性效应附近均会出现边界层,1区和4区的气体处于静止状态不存在边界层.
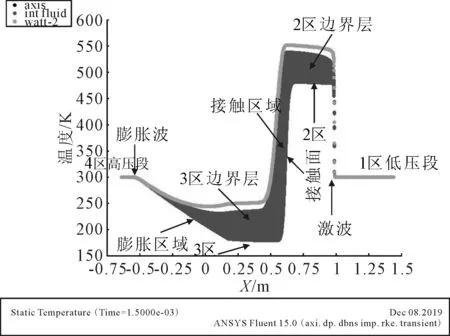
图7 t=1.50 ms时,沿轴向位置管内温度(K)分布范围(Case4:p4=500 kPa,p1=20 kPa,T4,1=300 K)
采用不同时刻的压力和温度云图来反映激波移动的过程,见图8~9,给出了激波产生、传播及反射过程中流体的压力和温度变化云图.t=0.1 ms时,膜片消失后,入射激波向低压段传播,经过的2区压力和温度迅速升高,膨胀波向高压段传播,膨胀波后的区域压力和温度会降低;t=1.0 ms时,由压力云图可以清晰观察到膨胀波和入射激波面的运行位置,根据温度云图可观察到入射激波与接触面之间的2区,随着时间推移,2区范围会逐渐增大,这是因为激波运行速度大于接触面前进速度;当t=2.5 ms时,入射激波抵达右尾端端壁并产生反射激波向左传播,经过的5区压力和温度再一次升高达到稳定状态并持续一段时间,膨胀波到达左端端壁后发生反射产生反射膨胀波向右传播;t=3.0 ms时,反射激波向左传播与接触面相遇并产生二次反射激波,二次反射激波向右传播;t=3.2 ms时刻,二次反射激波会对5区进行压缩作用,使5区压力和温度不均衡上升,试验区的气体状态发生改变,试验区环境被破坏,距尾端最远的测点压力稳定状态最先被破坏,当二次反射激波行至尾端端壁,5区有效试验时间结束;t=3.5 ms时,二次反射激波已到达尾端端壁,再次反射产生三次反射激波,这个过程会持续多次,直至激波管内整体压力处于平衡状态.
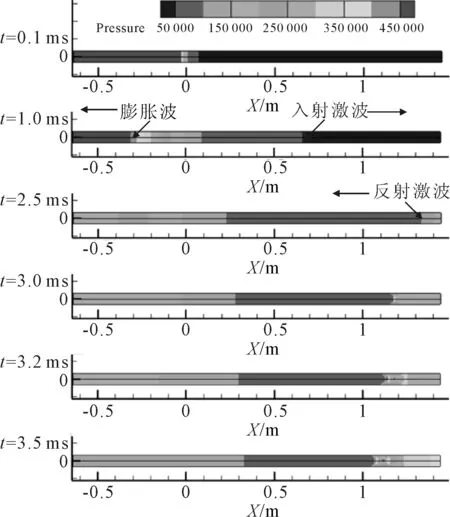
图8 Case4激波管内流体瞬时压力(Pa)云图

图9 Case4激波管内流体温度(K)云图
3.2 激波管5区试验时间限度的计算
以空气(理想状态)为例,计算移除高压段与低压段之间膜片后可以获得的激波管5区有效试验时间,将反射激波后的流动特性稳定的时间定义为试验时间,试验时间是评估激波管设备性能的重要参数,可为进行着火延时测量提供重要理论参考依据.
激波管中流体运动位置-时间平面图是一种重要的工具,它可以很好地估计在移除膜片后可获得的有效试验测试时间.图10~11为Case4(air-air,p4=500 kPa,p1=20 kPa,T4,1=300 K)运行时压力和温度分布的预测x-t图.图10压力分布x-t图中接触面没有出现,因为它连续的跟随入射激波后,图11为整个激波管设备的温度变化,激波、膨胀波和接触面都呈现在图中,激波之后是接触面,直到反射激波与接触面相互作用,然后被进一步反射.膨胀波到达左端壁面会产生反射膨胀波,由图11可知,膨胀波1曲线斜率小于和接触面的曲线斜率,即接触面传播速度大于反射膨胀波,因此,高压段长度足够条件下,反射膨胀波到达低压段末端之前,激波就已与接触面相交.二次反射激波到达右端壁面时,标志激波管测试时间结束.
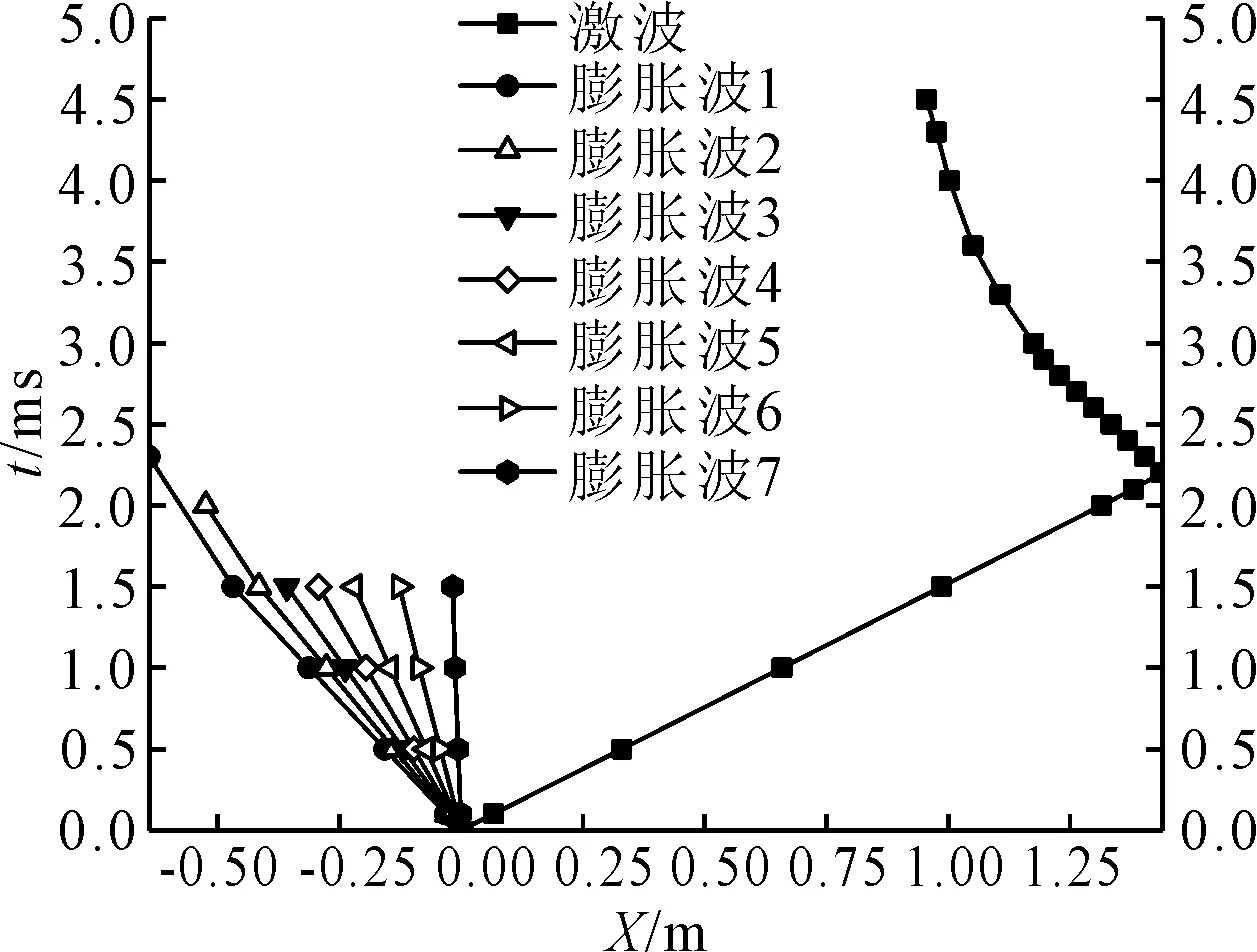
图10 压力云图中,激波的位置随时间变化曲线
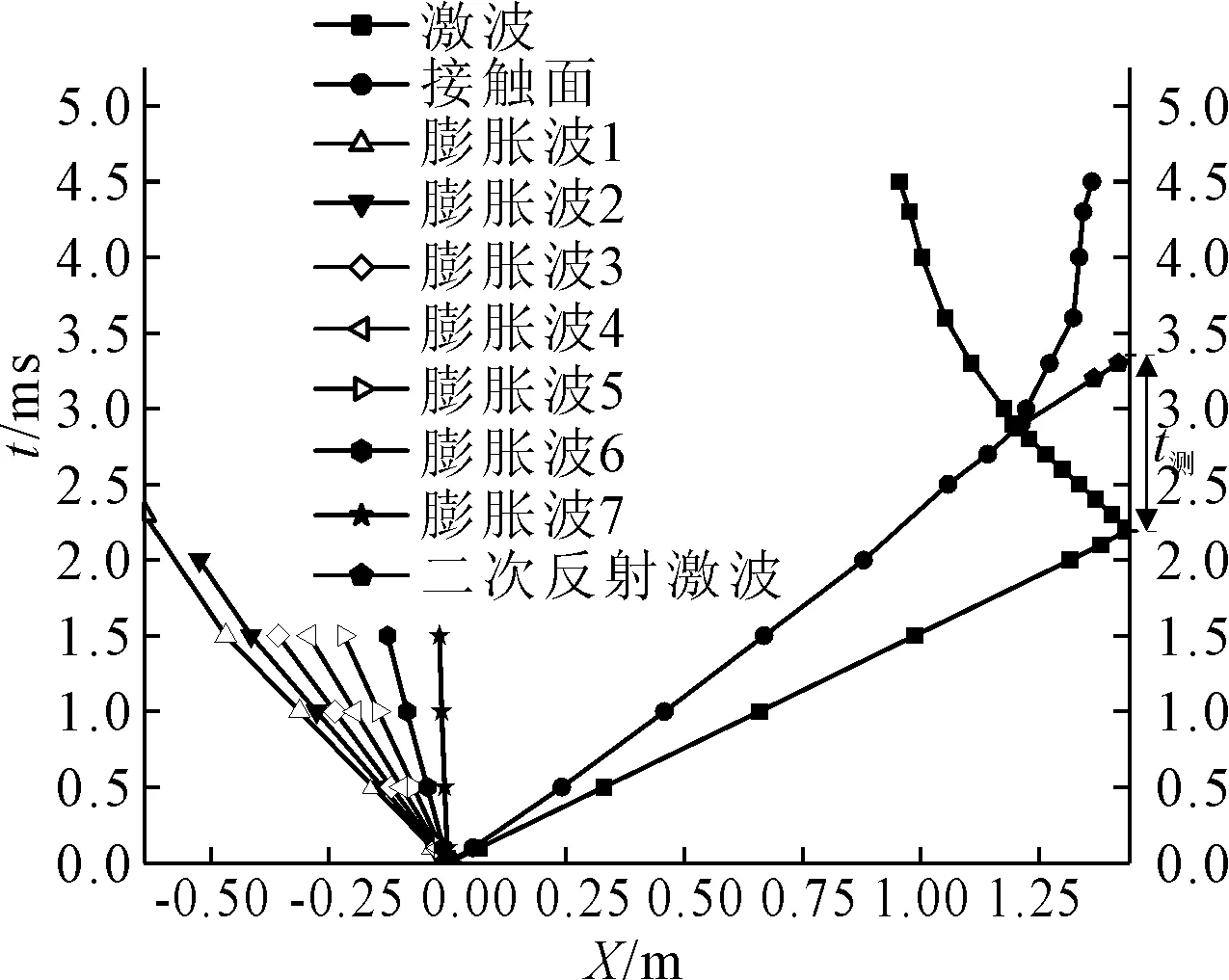
图11 温度云图中,激波和高低压段间的接触面的位置随时间变化曲线
在激波管壁面设置了8个监测点,另外在低压段端面中心设置了1个监测点,图12为Case4工况下激波管壁面监测点压力随时间变化情况.开始时,高压段测点S1保持初始压力不变,膨胀波经过后压力持续降低,待反射膨胀波达到时再次降低;低压段壁面测点S2~S8入射激波到达时压力均有阶跃升高,S6~S8处反射激波经过,S6处距尾端较远,反射激波已遇到接触面产生二次反射激波,反射强度下降,因此压力二次升高值低于测点S7、S8.测点S9不同于侧壁测点S8,只有一次压力阶跃过程,入射激波与尾端壁面相遇时刻就是5区的开始.
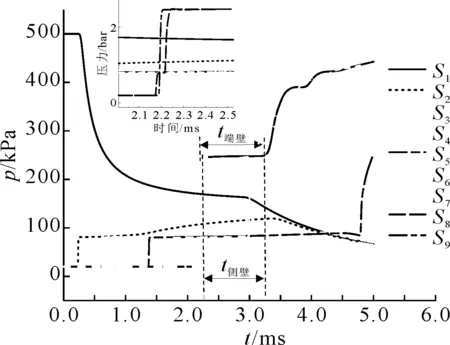
图12 激波管壁面监测点压力变化
实际试验过程中,通常有两种方式表示测量时间,分别为侧壁传感器压力稳定时间t侧和端壁传感器压力稳定时间t端,压力测点相当于实际设备上的压力传感器,以上方式也是5区试验时间限度的重要参考参数.表5为激波管试验时间限度计算结果比较.

表5 激波管试验时间限度计算结果比较
由表5可知,该工况下几种试验时间限度估计方式得出的结果差异较小,侧壁测点S8得到的压力稳定时间为1.039 ms,比端壁测点时间S9压力稳定时间1.073 ms要短,这是因为边界层效应的影响,反射激波会发生激波分岔和激波衰减,离反射端面处的距离越近,受边界层影响越小,侧壁测点压力开始上升至稳定的时间稍长于尾端端壁测点.然而,激波管在该算例下x-t图得到的测试时间为1.169 ms,大于端壁测点的压力稳定时间,综上所述,该算例理论有效试验时间为1.169 ms,实际测量有效试验时间最大为1.073 ms.
4 结 论
1) 采用FLUENT中的湍流模型进行激波管流体流动数值模拟,计算结果与层流模型模拟结果以及实验结果进行比较,与实验结果吻合较好,表明湍流模型对激波管流动具有较好的模拟效果,本文CFD数值方法是高效可靠的.
2) 详细模拟了激波的产生和传播过程,给出了激波形成、传播、反射和激波与接触面相互作用的整个过程,接触面与反射激波相遇时刻和二次反射激波行至端壁的时间是有效试验时间限度的重要影响因素.
3) 本数值方法能够提供x-t关系图,从该图中可以确定激波管实验测量有效持续时间,激波管5区内侧壁、端壁压力传感器测得的试验时间长度均小于x-t图获得的最大的测试时间,且差值较小,符合预期结果.
