基于多目标优化的系泊系统设计

金珈辉，刘永慧

（上海电机学院电气学院，上海201306）

随着新能源需求的不断增长，风电行业的发展不断加速，相关的近浅海浮式风电研究成为学者们的研究热点。对于浮式风电平台而言，近浅海的气象观测尤为重要，观测网络的传输节点由浮标系统、系泊系统和水声观测通信系统组成。其中系泊系统由钢管、钢桶、重物球、锚链和抗拖移锚组成，水声通信观测系统安装在系泊系统的钢桶内［1］。针对通信方面，通信传播效果在钢桶轴线与竖直线重合时达到最大［2］。对于观测过程，观测精度随着钢桶水平漂移半径的减小而增强［3］。因此，优化观测通信器竖直倾斜角和水平漂移半径，有助于提高系统的观测和通信性能。

张华杰等［4］通过对悬链线进行受力分析，建立悬链线标准方程，并分析不同应力情况下系泊系统的数学模型，考虑约束条件对锚链形态优化求解。Touzón等［5］针对浮标与系泊系统之间产生的动态张力进行分析，避免拟静态分析在张力方面的不准确性，并将线性化运动耦合模型应用于双体浮杆型振荡水柱，通过与等效时域仿真结果进行比较，验证该方法在张力方面的准确性。以上研究主要通过模拟构件的张力进行悬链线的近似建模，但悬链线模型的误差极易受到构件数量和近海气候的影响。因此后续通过分析构件的应力，建立系统的受力分析模型。Monteiro等［6］针对用于超深水油气开采的浮式生产系统（FPS）在非对称布局下的大量立管，建立确保立管完整性的系泊配置优化模型，利用跟踪中心轨迹内点法进行求解，有效地处理了非线性约束。王志东等［7］通过对内转塔内部结构进行数据化，引入系泊缆预张力等参数，分析外部荷载对单点系泊系统的动力效应影响。

上述研究均针对单一材料的系泊系统进行模型优化，而对于复合材料的系泊系统，模型的计算量较大。为提高系泊系统的观测和通信性能，优化系泊系统的结构设计，减小模型的计算复杂度，本文首先进行力学计算得出构件所受的外部荷载，对构件进行受力和力矩分析，并通过联立方程组，推导出构件倾斜角，进而简化数学计算。然后以通信器倾斜角为底层优化目标，水平漂移半径为上层优化目标，建立多目标优化模型。最后分析最优解的分布特性，引入基于粒子群和人工鱼群的混合优化算法，综合利用粒子群优化（Particle Swarm Optimization，PSO）算法的局部收敛性和人工鱼群算法（Artificial Fish Swarms Algorithm，AFSA）的良好全局性，使计算的收敛速度加快，结果更加精确。

1 力学模型

1.1 基本假设

为简化问题，便于模型的建立与求解，针对图1系泊系统提出以下假设：

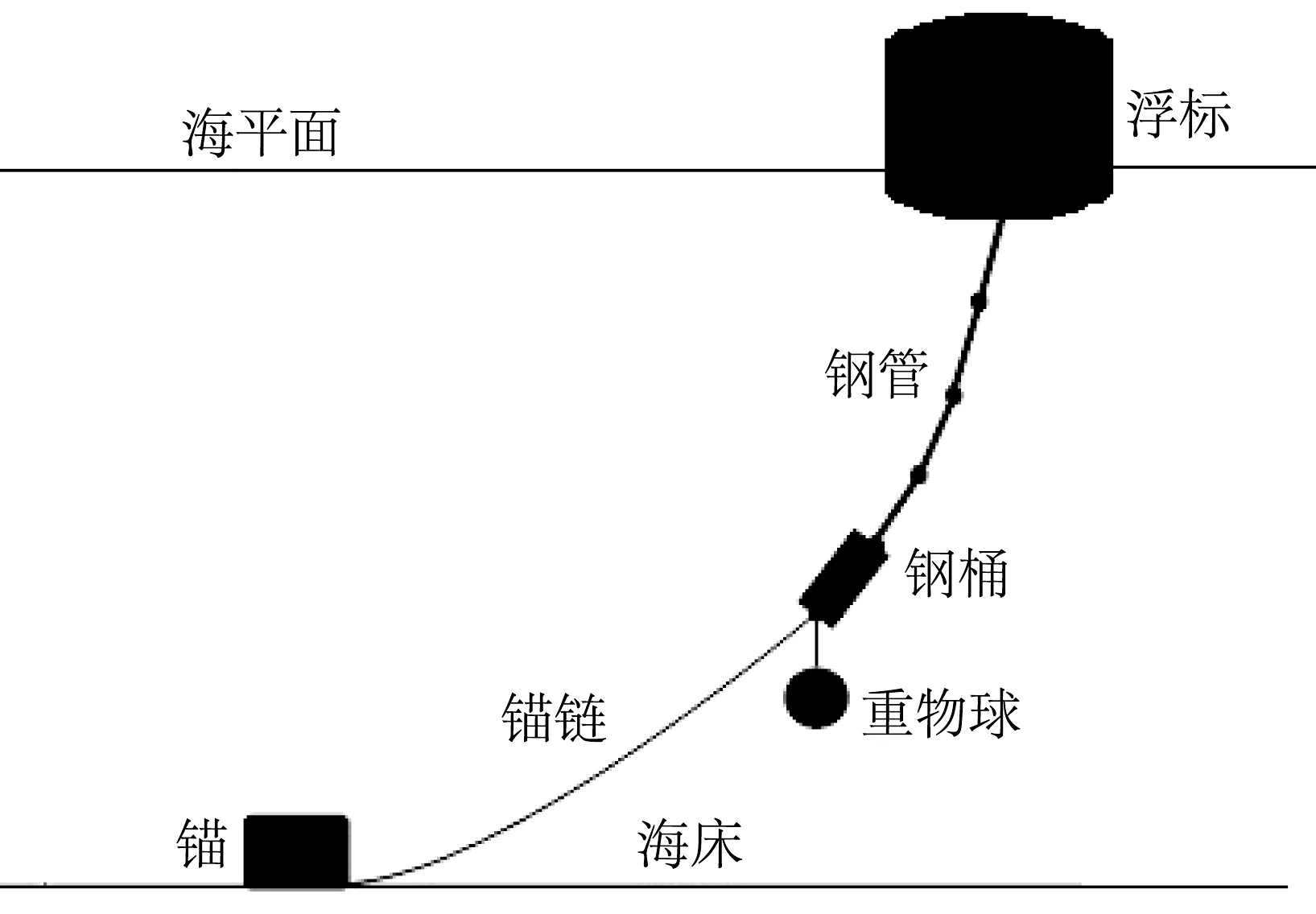
图1 系泊系统示意图

（1）假设锚链所受到的浮力可以忽略。

（2）假设重物球可以看作一个质点，即只有质量，体积忽略不计。

（3）假设锚链末端切线方向与海床夹角不超过特定角度时锚不动。

1.2 力学计算

分析系泊系统所受外部环境，构件易受到风和水流外力的作用发生倾斜。本节将系统所受外力，以构件所受荷载的形式导入优化模型。

1.2.1 近海荷载 相对于物体内应力，荷载是使物体产生形变的外力，为施加在工程结构上使物体产生效应的同种直接作用力的总和，近海的浮标和构件只受到风荷载和水荷载作用。

（1）风荷载。风荷载也称风的动压力，是空气流动对工程结构所产生的压力。由文献［8］近似公式可得近海风荷载为

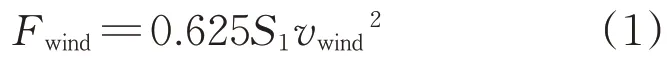
式中：Fwind为构件所受近海风荷载；S1为物体与风的有效接触面积；vwind为风速。

（2）水荷载。水荷载也称水的动压力，是由于水流的质量及流速而产生的力。由文献［9］近似公式可得近海水荷载为

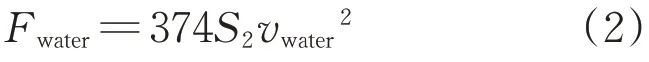
式中：Fwater为构件所受近海水荷载；S2为物体与水的有效接触面积；vwater为水流速度。

1.2.2 构件浮力 浮力为物体在流体内各表面受流体压力的总和，即物体所受的浮力等于物体下沉静止后排开液体的重力。构件所受浮力为[10]

式中：Fb为构件所受浮力；ρ为海水密度；g为重力加速度；V为构件入水体积。

1.3 力学分析

本节对系泊系统各构件进行力学分析，结合构件近海所受风荷载和水荷载，建立各构件的受力平衡和力矩平衡方程。

1.3.1 受力平衡 力学系统中，受力平衡是指在参照系内，物体保持静止或匀速直线运动状态。基于假设条件，对构件进行受力分析，构件的受力示意图（示意图仅表示力的方向，不表示力的大小）如图2所示。

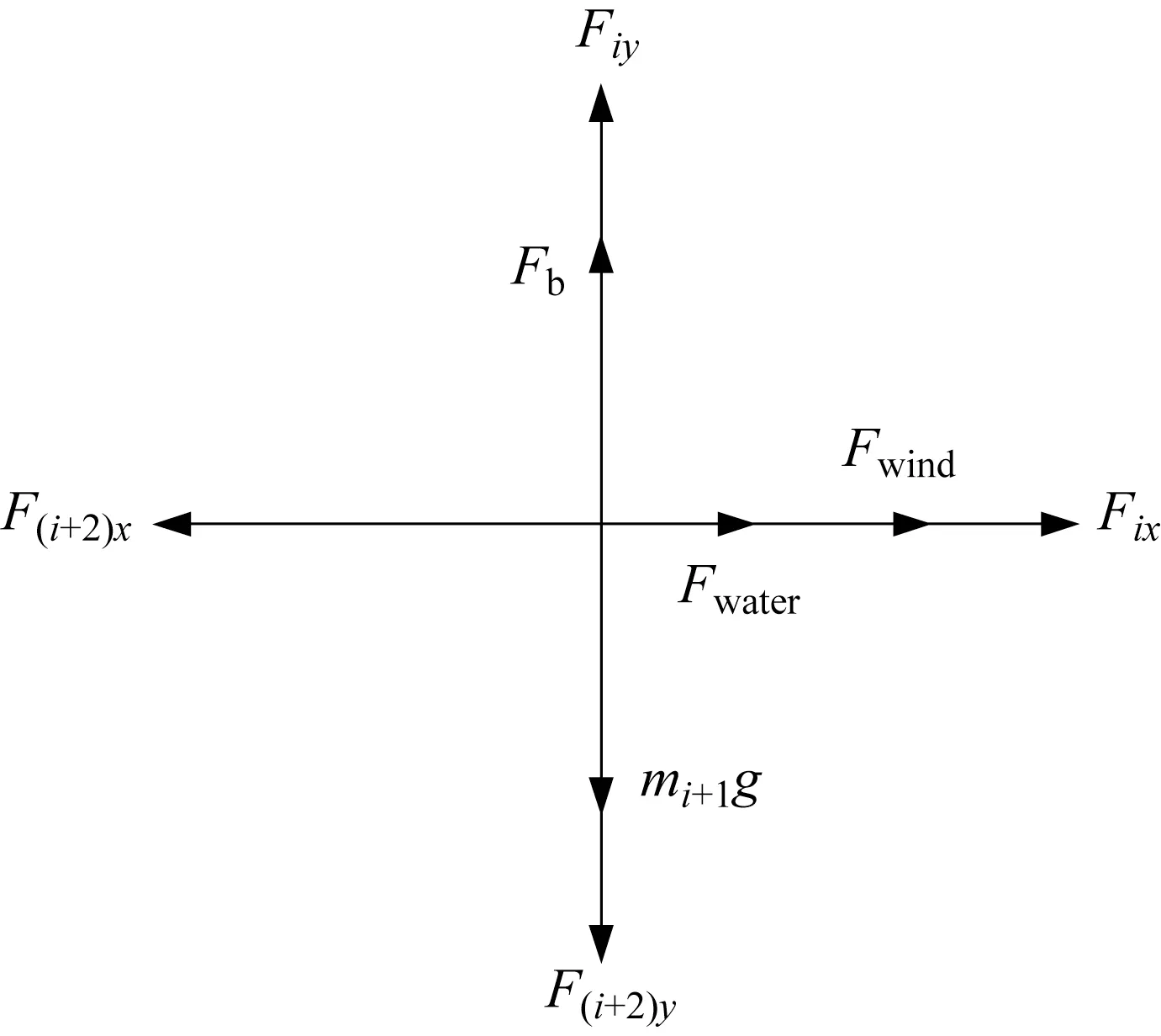
图2 构件受力平衡示意图

将力分解得到浮标受力平衡方程为

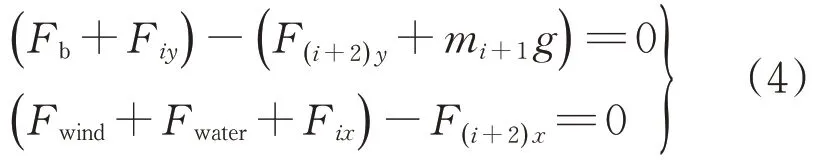
式中：mi+1为构件i+1的质量；F iy、F ix和、分别为构件i和构件i+2拉力在y轴和x轴分解后所得的力；i为构件编号，取值范围为i=1，2，…，q，q为构件总数。

1.3.2 力矩平衡 物体上的作用力与力臂的乘积称为力矩。稳定的系泊系统应满足力矩平衡，为便于模型简化，选择构件与上一构件相连节点作为支点进行分析。

根据力学力矩平衡公式［11］，可得钢管与钢桶力矩平衡方程为

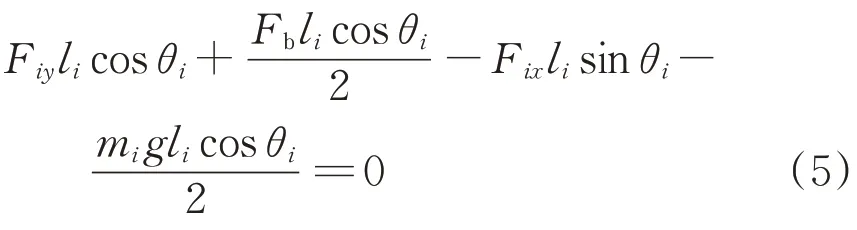
式中：l i为构件长度；θi为构件末端与水平面夹角；mi为构件i的质量。

1.4 模型简化

联立式（4）、式（5），可得受力平衡和力矩平衡方程组，但方程组的计算复杂度会随着构件数量呈现指数级别的上升。为降低计算的空间复杂度，对构件倾斜角化简可得

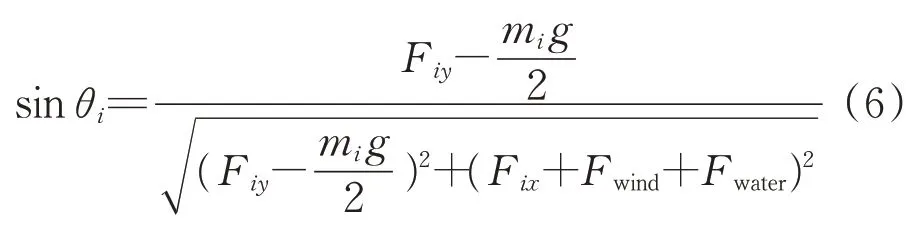
可见式（6）降低了求解计算的空间复杂度。由于近海系泊系统遇到风浪会产生动态激发运动，因此系泊系统的设计需要确保水深，同时不影响通信和观测。本文采用海水深度进行求解，提高了模型的实际应用程度。海水深度等于构件垂直方向投影之和，即

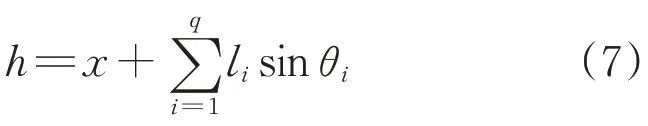
式中：x为浮标吃水深度。

2 系泊系统优化

通过分析系泊系统构件可知，构件增多，钢桶倾斜角减小，水声通信效果提高，但构件的增多会造成漂移半径增大，降低观测效果。考虑到设备运行的质量要求，需同时对水声通信器倾斜角和漂移半径进行优化。因此，系泊系统的优化设计可以描述成以下多目标优化问题，同时实现通信器倾斜角和漂移半径最小化目标。

2.1 通信器倾斜角

2.1.1 目标函数 系泊系统的水声通信器，其工作原理是通过模拟转换器将采集的信息转换成电信号，又通过电转换器将电信号转换为声音信号；声音信号通过介质将声音信息传递到声音接收器，将声音信号又转换为电信号，最后通过电反转器将电信号还原成采集信息［12］。相比有线通信来说，水声通信速率低，且易受干扰，因此减小通信器倾斜角保证通信质量，是保证数据采集的前提，其目标函数为

式中：e为通信偏正量；θ5为钢桶与水平轴夹角。

2.1.2 约束条件 由流体力学理论可知，当重物球质量增大时，通信器倾斜角减小。但重物球质量过大时，浮标沉入水中，会导致观测节点丢失。因此通信器倾斜角需满足重物球质量约束如下：

①上限。仅挂重物球就能使浮标恰好没入水中，即

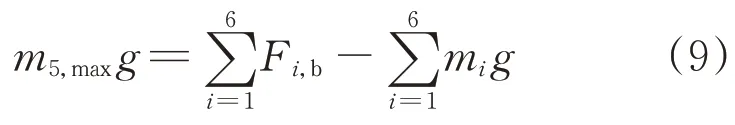
式中：m5，max为重物球上限质量；F i，b为构件i所受浮力。

②下限。系统无需挂重物球就能达到稳定效果，即重物球下限质量m5，min=0。

2.2 漂移半径

2.2.1 目标函数 由于观测端与被观测端的相对运动，使观测信号的频率发生变化。除了设备的相对运动外，起伏的海面、无规则的海洋状况对观测信号的回收也会引入多普勒频移，导致多途效应非常明显。为增加设备的观测精度，减小多途效应，本文通过构件的长度和倾斜角度，计算构件在水平方向的投影长度，得出其漂移半径目标函数为

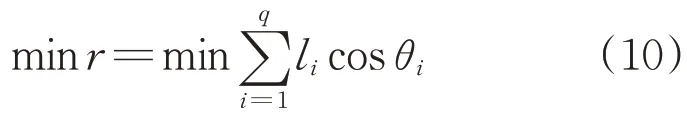
式中：r为漂移半径。

2.2.2 约束条件 分析式（10）可知，锚链过多时，漂移半径增大，导致观测精度降低；而锚链过少时，由于锚链末端、锚链接处的切线与海床的夹角超过特定角度，锚被拖行，会致使节点移位丢失。因此漂移半径需满足锚链节数约束和节点稳定性约束如下：

（1）锚链节数约束。

①上限。当不挂重物球且浮标恰好完全没入水中时锚链的长度达到上限，即

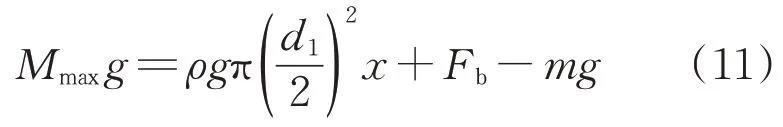
式中：Mmax为锚链的总质量。

依据锚链总质量、线密度和单节锚链长度，得到锚链节数的上限，即

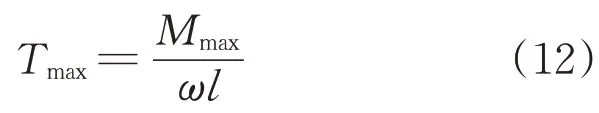
式中：ω为锚链的线密度；l为单节锚链长度。

②下限。假设此时钢管、钢桶、锚链处于同一竖直线，可得锚链节数的下限为

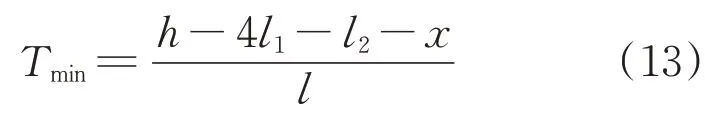
式中：l1为单节钢管长度；l2为钢桶长度。

（2）节点稳定性约束。该系泊系统工作时，要求锚链末端、锚链接处的切线方向与海床的夹角不超过特定角度θmax，以此角度为约束条件得

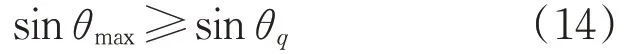
式中：θq为连接拖锚的锚链与水平轴夹角。

2.3 目标函数

综合式（7）～式（14），对目标设置权重，将多目标优化转化为单目标优化，建立的目标优化模型如下：

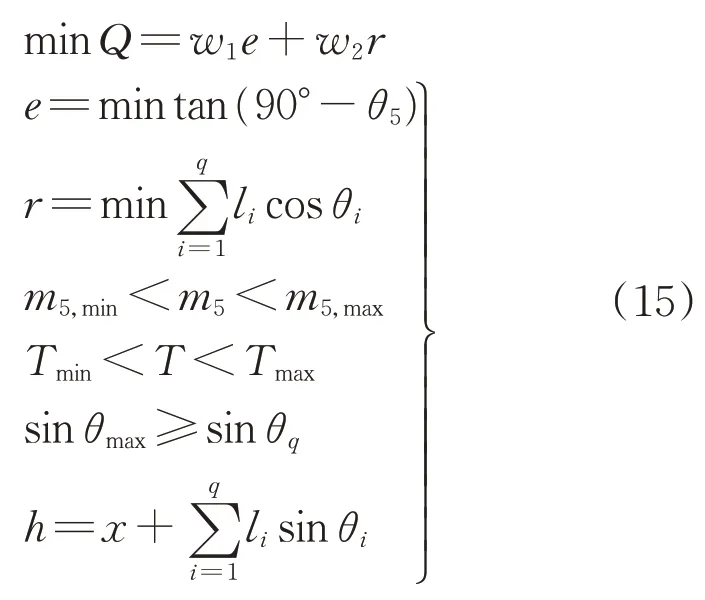
式中：w1、w2分别为通信器倾斜角和漂移半径的优化权重；T为锚链节数。

3 混合优化算法

考虑到多目标优化模型的求解计算量较大，由此引入智能优化算法进行辅助求解。通过分析可知，单一材料的系泊系统优化模型具有单调性，可以通过PSO算法进行求解。但对于复合材料，建立的系泊系统优化模型不具有单调性，单纯采用AFSA求解非单调模型，收敛速度较慢［13］。因此引用人工鱼群和粒子群的混合优化算法（PSOAFSA），结合PSO算法的局部收敛性［14］和AFSA的全局对比性［15］，提高算法的收敛速度和精度。

分析解空间的局部单调性，将鱼群设置为精英群和普通群，以AFSA和普通群探索局部最优区域，再通过精英群将局部最优区域传递给PSO算法，并快速收敛至局部最优解，从而加快全局最优解的计算。

（1）初始化。设置人工鱼群初始位置状态X={X1，X2，…，XN}，视野半径Vs，移动步长S，鱼群拥挤限度δ，最大试探次数nmax；设置粒子群惯性权值ωp，加速度参数c1和c2。

（2）设置公告板。计算个体人工鱼的适应度值Y，得最优值Yb记录在公告板内。

（3）粒子群。根据适应度值排序Y，选出前T1个作为精英群p1，按PSO算法进行更新，得最优适应度值Pb和新种群。

（4）人工鱼群。精英群之外的普通群p2，按AFSA算法进行更新，得最优适应度值Ab和新种群。

（5）更新公告板。比较Pb和Ab的适应度值，得到最优值，并与公告板上Yb比较，如优于Yb，则更新公告板，否则不变。

（6）终止条件判断。重复（3）～（5）步，直到公告板上的最优解满足误差条件。

（7）算法终止。输出最优解（即公告板上适应度值及个体位置）。

通过式（6）对倾斜角化简，引入混合优化算法，从而降低力学模型计算的时间和空间复杂度。在约束条件下，以通信器倾斜角和漂移半径为多目标进行全局搜索，求解出最优的锚链型号、长度和重物球设计方案。

4 算例分析

设定钢桶的倾斜特定角度为5°，锚链末端的倾斜角度小于16°时，系统不会被拖拽偏移。以最大水速1.5 m/s，最大风速36 m/s为近海水域背景条件，表1锚链数据为选择范围，进行混合优化算法的求解。

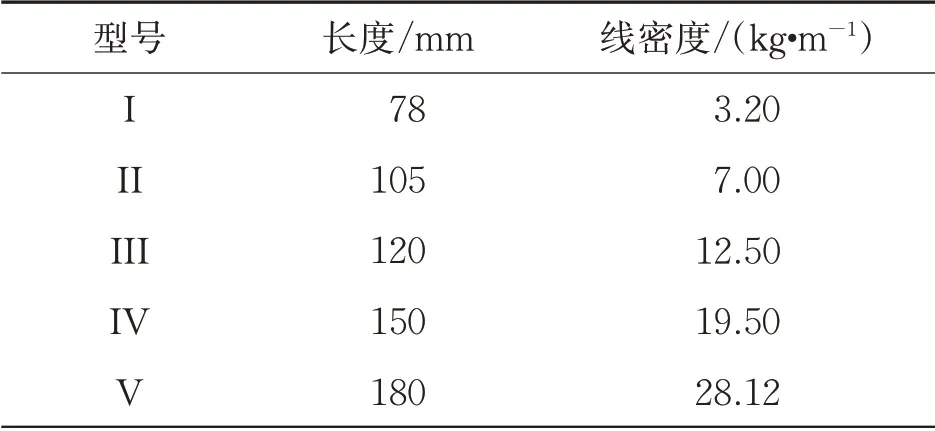
表1 锚链型号和参数

综合考虑目标函数的重要程度，求解上述优化模型，部分搜索结果如表2所示。

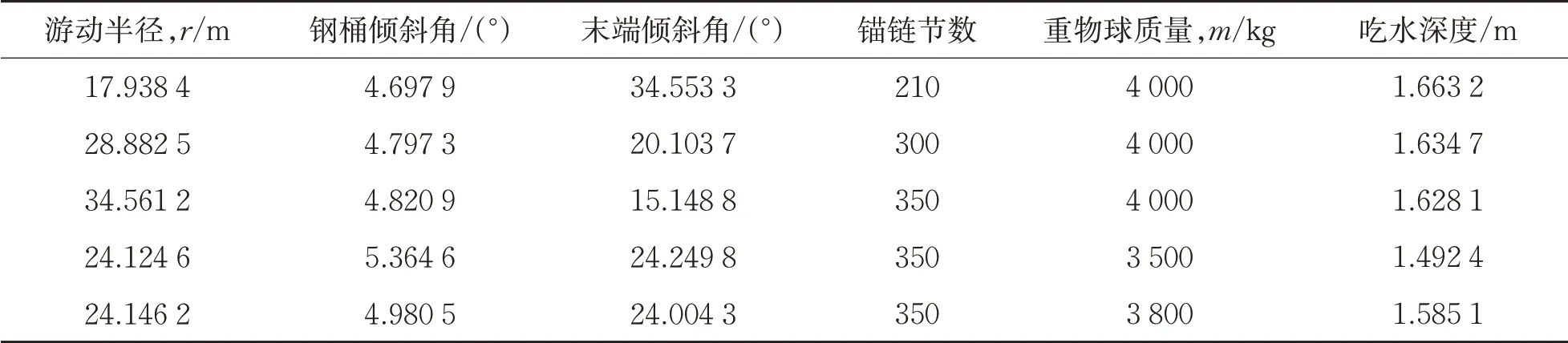
表2 型号I锚链部分迭代结果

选取V型号的锚链19.8 m，重物球3 500 kg作为系泊系统最优设计。该设计在风速36 m/s，水流速度1.5 m/s，水深20 m的情况下，钢桶倾斜角度为4.853 3°，钢管倾斜角度从上到下依次为4.631 3°、4.698 2°、4.765 4°、4.832 8°，浮标的吃水深度为1.619 1 m，浮标的游动半径为14.281 m，锚链末端的倾斜角度为15.778 6°。

为了对比混合优化算法的计算性能，将AFSA、PSO算法和PSO-AFSA连续运行30次所得函数最小适应度值的平均误差和平均迭代次数作为对比指标，测试结果如表3所示。

由表3可知，PSO算法迭代速度最快，但易陷入局部最优，导致结果误差较大；AFSA误差最小，但迭代次数过多，计算效率较低；PSO-AFSA迭代次数比PSO算法略高，结果误差比AFSA算法略高，但综合了两者的计算效率和精度。为进一步检测算法的有效性，建立误差随迭代次数的变化趋势，如图3所示。

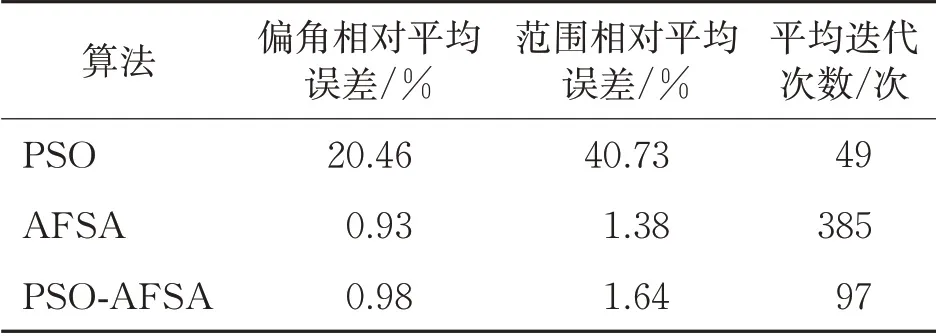
表3 不同算法测试结果比较

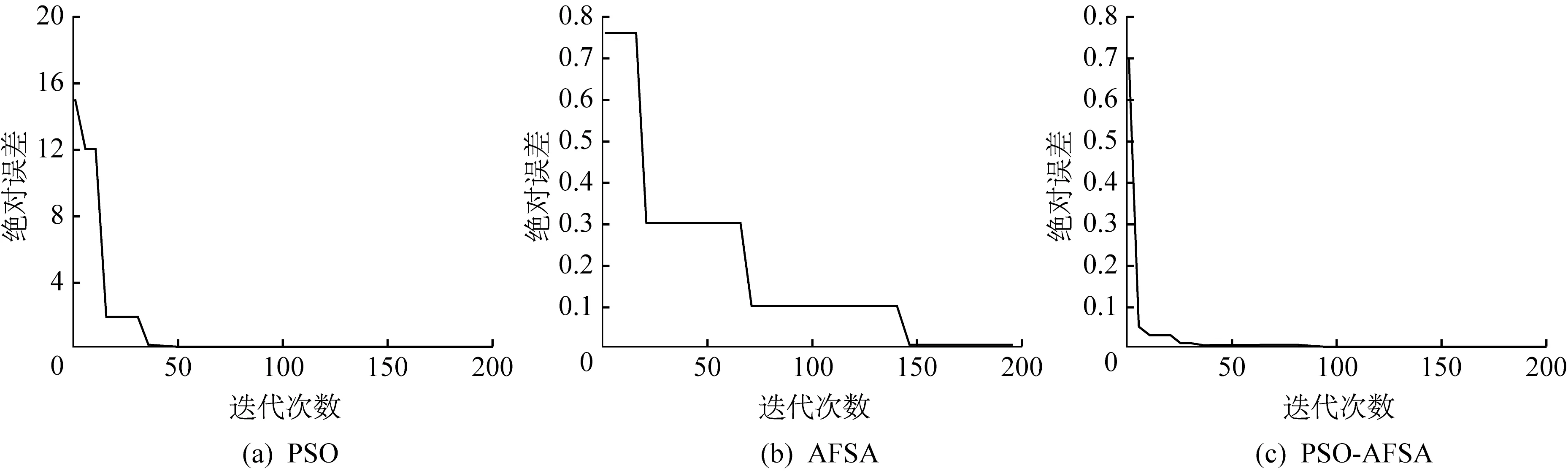
图3 适应度误差变化曲线

由图3可知，PSO算法收敛速度过快，陷入局部最优，导致结果误差较大；AFSA算法迭代过程中滞留时间过长，导致迭代速度较慢；PSO-AFSA不仅收敛速度快，而且求解精度高。

5 结 论

本文通过分析海水深度、海水浮力、风荷载以及水荷载，建立了系泊系统的力学平衡模型。以系泊系统的采样稳定为目标，建立了以通信器偏角和游动范围为优化目标的模型，并引入PSO-AFSA进行模型求解。对单个构件进行力学分析建立优化模型，并通过PSO-AFSA优化算法提高计算效率和计算精度，设计出系泊系统的最优设计方案，为一定范围内近海海域情况提供了参考方案。