基于改进蚁狮算法的分布式电源选址定容方法
2021-07-07高桂革文传博
柳 康,高桂革,文传博
(上海电机学院电气学院,上海201306)
分布式电源(Distribution Generation,DG)接入配电网后,因自身的灵活性和可持续性,能有效缓解传统配电网与能源配置之间的矛盾[1],支撑节点电压,改变潮流方向,改善网络损耗。DG与大电网结合是一种节能减排、绿色环保的电力系统运行方式[2]。但是,DG的安装位置及容量配置不当时,对电力系统也是一种负担。
目前,很多学者从不同角度对DG选址定容问题进行研究。文献[3]采用隐式编码方式的遗传算法,以投资总成本最小为目标函数进行计算验证,但是DG的数量及接入位置需再次计算,增加了计算量。文献[4]考虑负荷不确定性,利用场景分析方法对大规模场景进行缩减,得到典型的场景及场景概率,虽然加快了计算时间,但是计算结果不够精确。文献[5]采用双层优化的方式进行优化计算,上层以年综合成本最小为目标函数,下层以有功切除量最小为目标函数,由于计算过程太过复杂,容易出现维数灾难。文献[6]以网络损耗、电压及电流的稳定指标为目标函数,将蒙特卡洛准则引入天牛须算法,增加了算法的稳定性,但算法的收敛性差,迭代次数较多。利用上述文献进行DG的选址定容计算时,或多或少存在一些缺陷,DG的最优位置和容量问题不能得到最好的解决。
本文将粒子群算法(Particle Swarm Optimization,PSO)中粒子的位移方式引入传统蚁狮算法(Ant Lion Optimization,ALO),并在蚂蚁种群的生成过程中引入动态比例调节参数。对ALO全局遍历性差、易陷入局部最优等缺点进行改进,提出改进ALO。以IEEE-33节点为算例,利用改进ALO进行DG的选址定容计算,并与遗传算法(Genetic Algorithm,GA)和PSO计算结果进行比较。
1 目标函数及约束条件
1.1 目标函数
从配电公司的角度出发,建立年综合成本最小的DG选址定容模型:
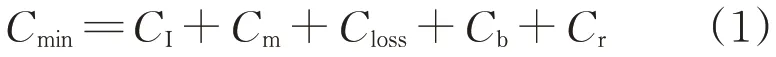
式中:Cmin为最小年综合成本;CI为DG投资费用;Cm为运行维护费用;Closs为有功网损费用;Cb为向上级电网购电费用;Cr为政府补贴费用。
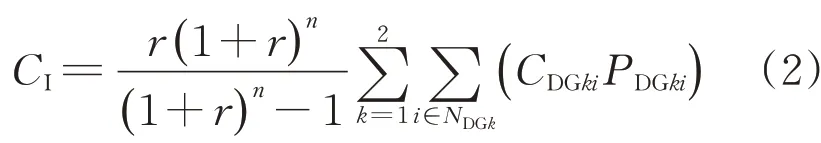
式中:r为贴现率;n为规划年限;k为DG类型,取1或2代表风力(WT)和光伏(PV)发电;NDGk为第k种DG可以安装的节点集合;CDGki为第i个节点第k种DG单位容量投资成本;PDGki为第i个节点第k种DG的安装容量。运行维护费用为
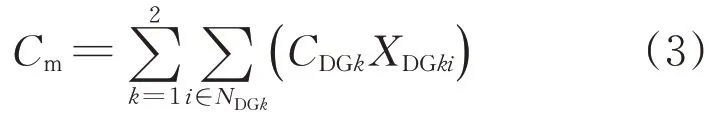
式中:CDGk为第k种DG单位发电量所需维护费用;XDGki为第k种DG在节点i的年发电量。有功网损费用为
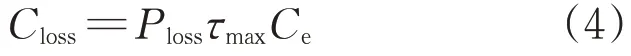
式中:Ploss为接入DG后配电网的有功损耗;τmax为最大负荷损耗小时数;Ce为单位电价。向上级电网购电费用为
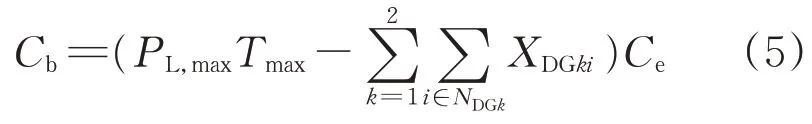
式中:PL,max为配电网有功负荷最大值;Tmax为最大负荷利用小时数。政府补贴费用为
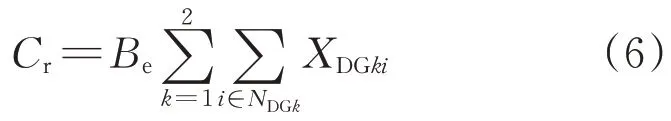
式中:Be为DG单位发电量的政府补贴费用。
1.2 约束条件
(1)等式约束。各节点的潮流约束方程为
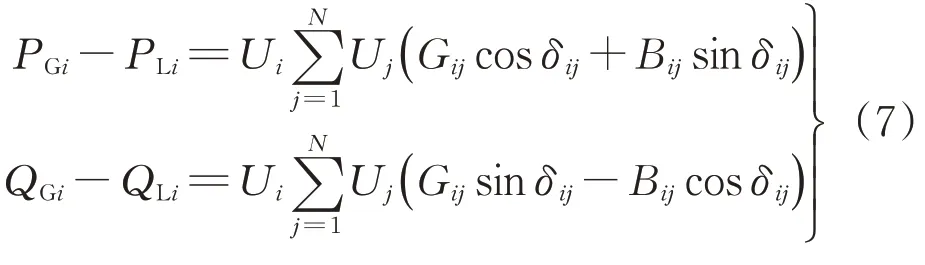
式中:PGi和QGi分别为节点i注入的有功和无功功率;PLi和QLi分别为节点i的有功和无功负荷;U i和U j分别为节点i和j的电势差值;Gij和Bij分别为线路导纳的实部和虚部;δij为功率因数角。
(2)不等式约束
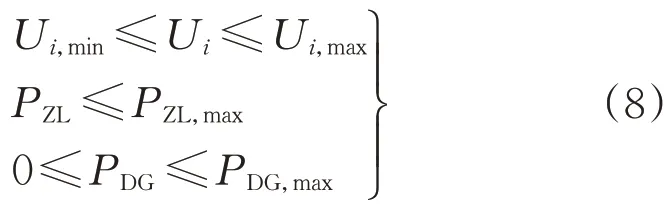
式中:Ui为节点电压;U i,max和U i,min为节点电压的上下限;PZL为支路产生的有功功率值;PZL,max为支路产生的有功功率最大值;PDG为DG接入容量;PDG,max为允许配电网接入DG的最大有功功率[7-8]。
2 对ALO的改进
2.1 ALO
ALO是澳大利亚学者Mirjalili于2015年提出的新型算法。ALO算法具有调节参数少、收敛准确度高和鲁棒性好等优点,是一种新型群体智能算法[9]。ALO算法实质上是一种仿生学算法,模拟蚁狮捕捉蚂蚁的过程:蚁狮在地下挖好陷阱,等待做不规律运动的蚂蚁掉入陷阱。蚁狮捕捉蚂蚁后会重新挖好陷阱,等待下一只蚂蚁。
ALO算法中每个蚂蚁代表待求问题的一个解,蚂蚁的随机游走就是对未知空间的搜索过程。每次迭代,蚁狮捕捉蚂蚁不断需求最优解,当蚂蚁的适应度低于蚁狮适应度时,则认为该蚂蚁被蚁狮捕获。在每一代的蚁狮中选出一个适应度最优的蚁狮作为精英蚁狮,下一代蚂蚁的位置由精英蚁狮和轮盘赌随机选择的蚁狮共同决定[10]。
本文采用十进制编码方式,蚂蚁和蚁狮都由待选节点和DG安装数量组成。每一个体的维数即为待安装分布式电源的节点数,每一维上的值为DG的安装数量。由于是两种DG选址定容,所以每个粒子的维数由原来的N变为2N。编码方式为
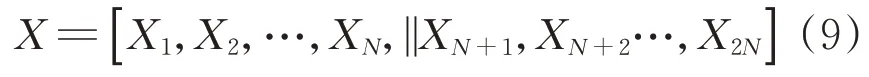
式中:X的前N个变量和后N个变量分别为各待选节点接入WT和PV的数量。
2.2 改进ALO
(1)优化轮盘赌选取值。ALO算法应用轮盘赌随机选择蚁狮进行随机游走,虽然增加蚂蚁的种群多样性,但是,有可能选中适应度较差蚁狮,降低算法的寻优效率。因此,对轮盘赌的适应度选取值进行约束,约束方式为
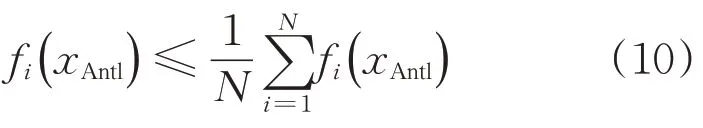
式中:fi(xAntl)为蚁狮适应度值。
如果fi(xAntl)≤蚁狮平均适应度值则参与轮盘赌,否则不参与轮盘赌选择。
(2)优化蚂蚁种群。ALO算法的优化过程就是在每一代最优解的周围进行寻优,试图找到更优解[11]。虽然不易陷入局部最优,但是全局遍历性不高,容易忽视蚂蚁与精英蚁狮之间的位置,错过更优解。受PSO全局寻优启发,在传统ALO算法蚂蚁游走步长基础上进行改进,增加种群多样性,改进方式为
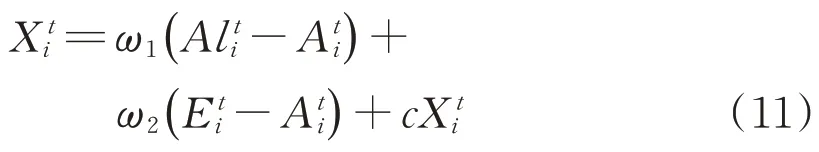
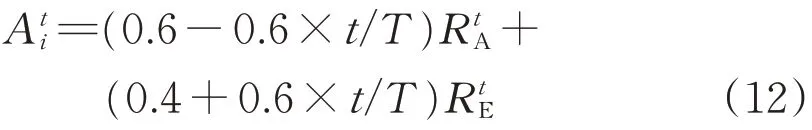
改进ALO的计算流程如下:
(1)输入配电网的原始数据、各种约束条件,确定蚂蚁和蚁狮的数目、最大迭代次数以及适应度函数维数和变量范围;
(2)初始化蚂蚁和蚁狮的位置,计算适应度值,找出其中适应度最优的蚁狮,将其视为精英蚁狮;
(3)围绕优化轮盘赌选择出的蚁狮以及当代最优蚁狮进行游走,然后通过式(12)更新蚂蚁的位置;
(4)计算位置更新后的蚂蚁的适应度,与蚁狮的适应度进行比较。若小于蚁狮适应度,蚁狮将其位置替换,并在蚁狮种群中选出适应度最优蚁狮为精英蚁狮。根据新的步长更新公式生成新的种群,并计算适应度值,直接与精英蚁狮适应度进行比较,选择适应度最小的值为精英蚁狮;
(5)判断是否达到最大迭代次数,达到最大迭代次数则停止迭代。
3 仿真验证
本文利用改进ALO和其他比较算法在IEEE-33节点系统进行仿真比较。IEEE-33节点系统如图1所示,该系统额定电压为12.66 kV,系统总有功负荷为3 715 kW,总无功负荷为2 300 kvar,DG装机总容量不超过系统总负荷的30%。系统规划年限为20年[14-15]。
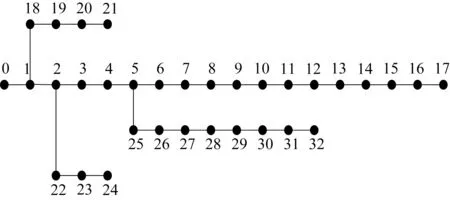
图1 IEEE-33节点配电系统
本算例中最大负荷损耗小时数τmax和最大负荷利用小时数Tmax都为5 000 h,单位电价为0.5元/kWh。本文假设DG可以安装的节点为7,15,17,18,25,29,30,31,32,33,DG的单台容量为50 kW,功率因数为0.9。WT的前期投资费用和运行维护费用分别为1万元/kW和0.1元/kWh;PV的前期投资费用和运行维护费用分别为1.3万元/kW和0.06元/kWh。考虑实际天气情况,WT和PV分别按额定容量的60%和50%投入运行。
表1为不同算法方案DG安装位置及容量。由表1可以看出,改进ALO、ALO、GA以及PSO计算得出的DG位置大都集中在配电网络末端。这是因为配电网络首端电压固定,末端线路电压容易低于配电网络允许电压下限。然而,当线路末端接入DG后,电压水平就会得到提升,首末端电压差减小,同时功率损耗也会大大减小。
表2为不同方案费用对比。由表2可以看出,接入DG与不接入DG相比,配电网向上级购电费用明显降低,且有功网损费用明显降低。这表明接入DG有利于节能减排。结合表1和表2可知,在5个方案中,改进ALO总费用最低。这是因为改进ALO得出更优的DG接入位置和容量,使得配电网络有功网损费用和向上级购电费用相较于其他方案更低。
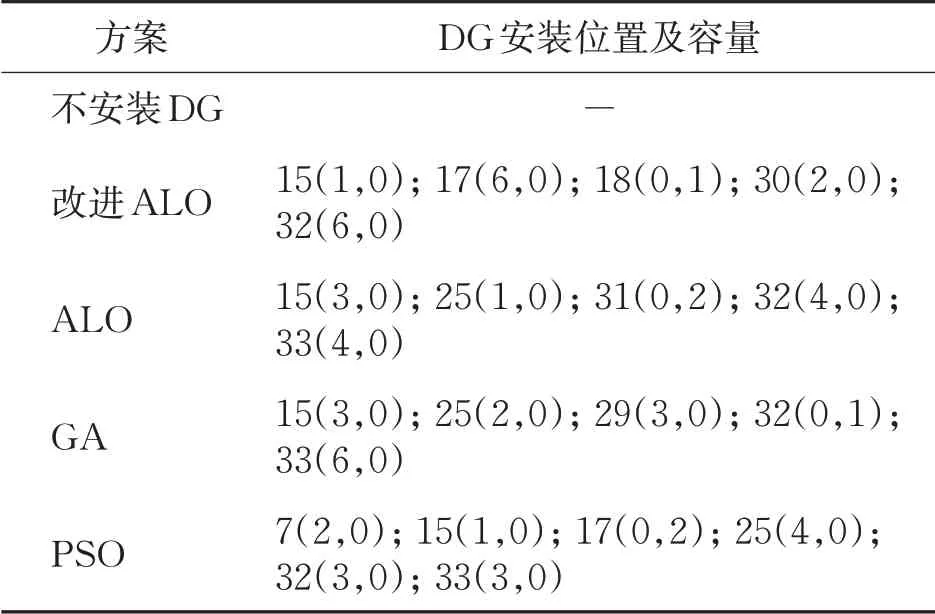
表1 不同算法方案DG安装位置及容量
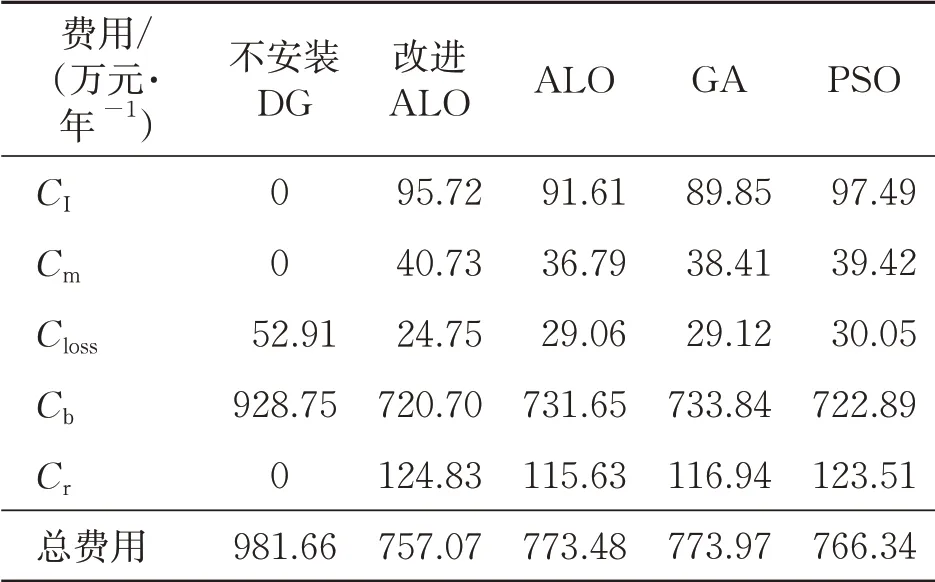
表2 不同方案费用对比
图2所示为不同算法迭代收敛曲线对比。由图2可知,采用改进ALO进行仿真计算,所得适应度最优,且收敛速度最快。这是因为改进ALO采用新的种群更新方式,拥有更好的全局遍历性;并且采用动态比例参数调整蚂蚁个体的生成过程,避免陷入局部最优解。相较于ALO在50代左右趋于平稳,改进ALO在30代左右趋于平稳,且适应度值更小,证明算法的有效性。
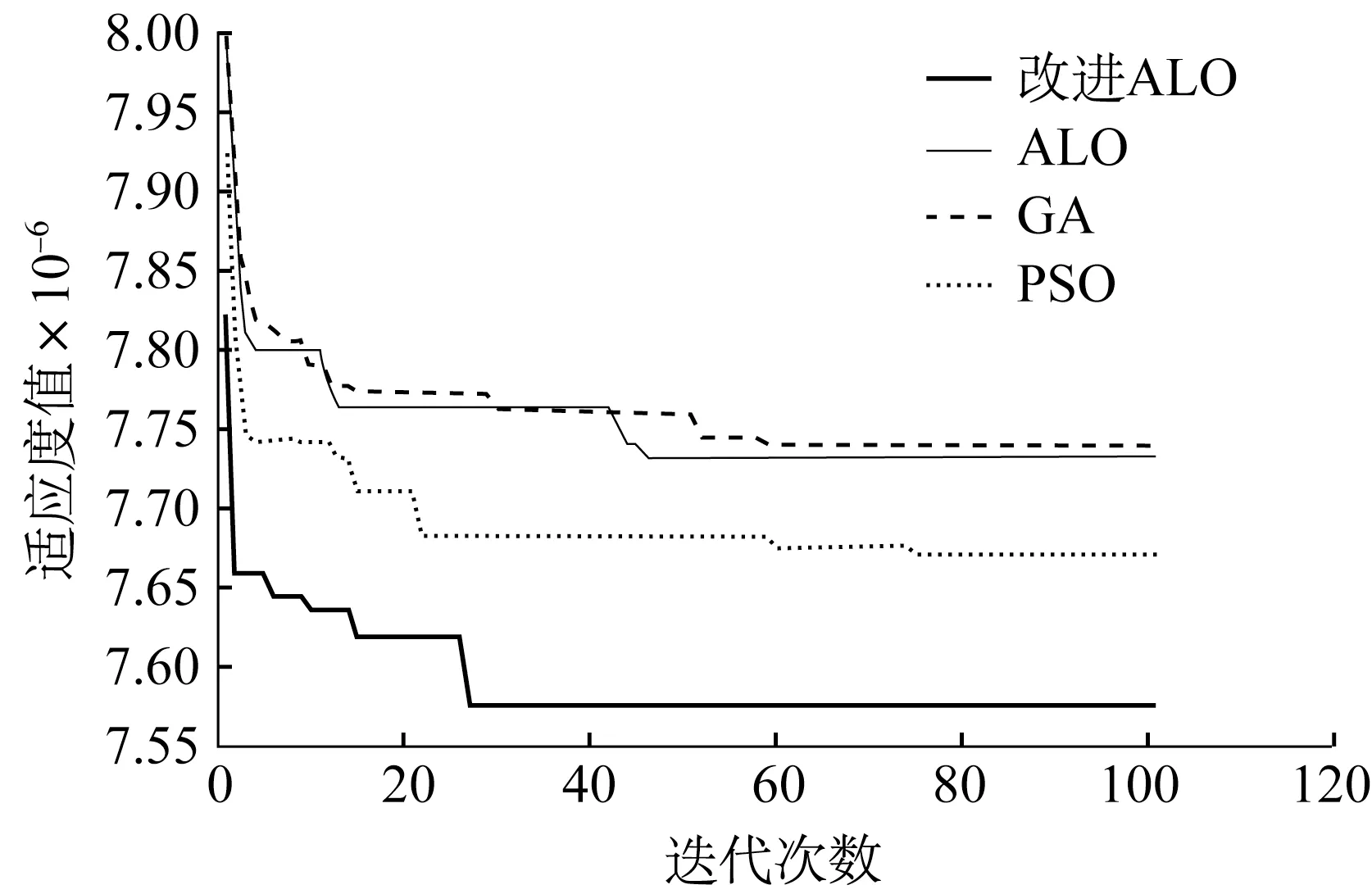
图2 不同算法迭代收敛曲线对比
4 结 论
本文建立配电网年综合成本最小目标函数模型,利用改进ALO、ALO、GA及PSO对目标函数进行计算。以IEEE-33节点为例进行仿真验算,得到以下结论:
(1)DG接入配电网可以降低有功网损,提高节点电压水平,有利于配电网安全稳定运行;
(2)相比于接入DG前,配电网年综合成本更小,说明DG有良好的经济效益,且有利于节能减排;
(3)改进ALO相对于ALO、GA及PSO收敛速度更快,且适应度值更优,算法有效可行。
