基于XGBoost算法的房价预测模型
2021-07-07王冬雪郭秀娟
王冬雪,郭秀娟
(吉林建筑大学电气与计算机学院,吉林 长春 130118)
0 引言
近年来,人们对房价的关注一直居高不下。由于城市化的加剧,对房屋租赁和购房的需求也持续增加,而房价问题不仅关系到人民生活水平,更是与国民经济发展息息相关。因此,对房价进行预测不仅对人们买卖房屋具有参考意义,而且对于政府进行房价调控也有积极作用[1]。因而确定一种可以精准反映房价走势的算法具有重要意义。
本文通过使用XGBoost算法来预测房价。通过对数据分析、预处理及基于XGBoost模型来构建房价预测模型。影响房价的因素多且复杂,如房屋面积、房屋地理位置、房屋户型等,本文仅选取对于房价影响较大的79个特征对房价预测模型进行评估,并选择RMSLE算法作为预测房价的评估算法。
1 数据预处理
在实际情况下,由于环境复杂等因素,我们获取的数据往往是存在缺失和异常的,因此,在建模前要对数据进行预处理。
1.1 数据集来源
该数据采集来源于Kaggle 2016年竞赛项目,分为训练数据和测试数据。其中训练数据中有1 460个样本,每个样本中含有80个特征,测试数据中包含1 459个样本,每个样本中有79个特征。
1.2 缺失值处理
对于数据的缺失问题,要考虑2个重要因素:缺失数据的情况是否普遍,丢失的数据是规律的还是随机的。数据的缺失可能意味着样本量的减少,这可能对我们接下来的分析和建模产生阻碍。因此,对缺失值的处理是必需的。对于不同的数据缺失机制,处理的方法也是不同的,常用方法分为数据填充和删除样本两大类[2]。对缺失值的统计如图1所示。本文所使用的数据缺失值不能确定是否是随机的,例如缺失比例最高的游泳池质量,可能是由于很多房子里并没有游泳池。因此根据缺失值的统计结果,本文通过删除缺失比例较高的变量及带有缺失值的样本对缺失值进行处理。
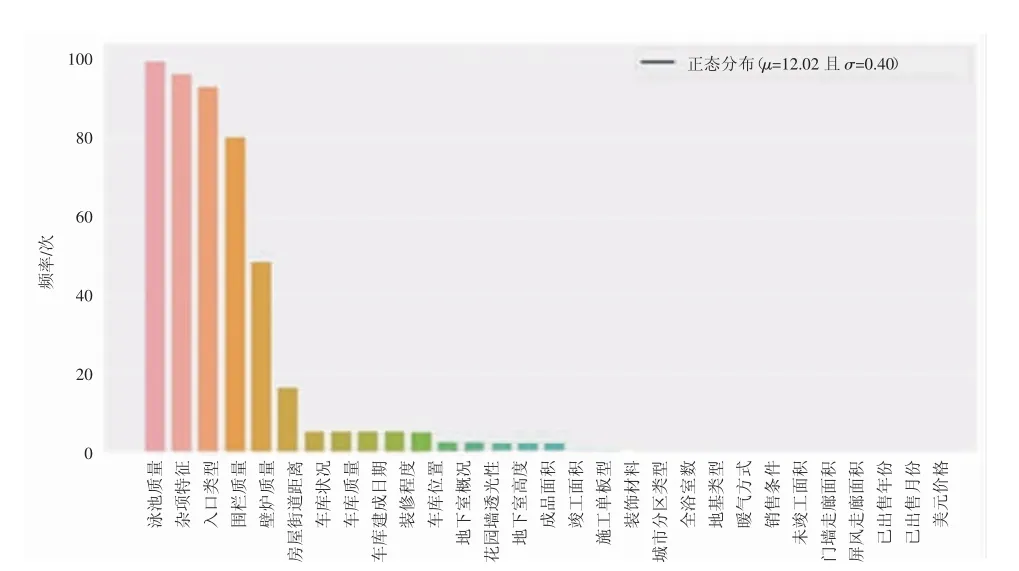
图1 缺失数据统计图
1.3 样本因自变量相关分析
本文所使用的数据集虽然给出了80个自变量,但是有些因素对房价的影响非常小,如果不进行筛选可能会影响结果的准确性[3]。因此,进一步筛选后,得出对房价最具影响的特征依次为:整体质量(整体材料和装修)、居住面积(地面以上)、车库容量、车库面积、地下室总面积、一楼面积、高档全浴室、客房总数(不含浴室)、建成年份。其相关矩阵热力图如图2所示。

图2 相关矩阵热力图
1.4 数据标准化处理
如图3所示,房屋的价格已经偏离了正态分布。因此,对于非正态分布,本文采用Box-Cox变换,使数据变得更“正常”。
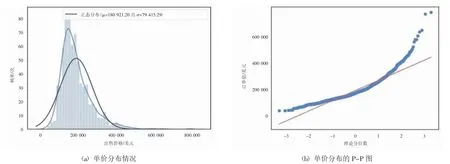
图3 原始数据分布
Box-Cox变换的一般形式为:

式中y(λ)为经Box-Cox变换后的响应变量,y为原始连续因变量,λ为变换参数。以上变换要求原始变量取值为正[4]。图4为经Box-Cox变换后分布。
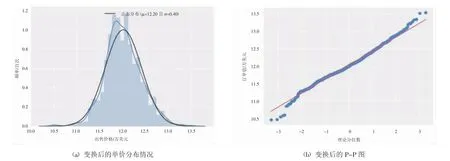
图4 变换后数据分布
2 XGBoost模型
XGBoost又称极端梯度上升,它是大规模并行Boosted Tree,是Gradient Boosting Machine的扩展,在相同的环境和条件下,XGBoost比同类算法快10倍以上[5]。XGBoost还可以通过分布式运算,进一步提高训练速度[6]。
2.1 基本模型
XGBoost是由k个基模型组成的加法运算式:

其中ft为k个基模型,为第i个样本的预测值。

其中n为样本数量。
模型的偏差和方差共同决定了该模型的预测精度,模型的偏差具体表现为损失函数,模型越简单则其方差越小,所以目标函数由模型的损失函数loss与抑制模型复杂度的正则项Ω组成,所以目标函数可表示为:
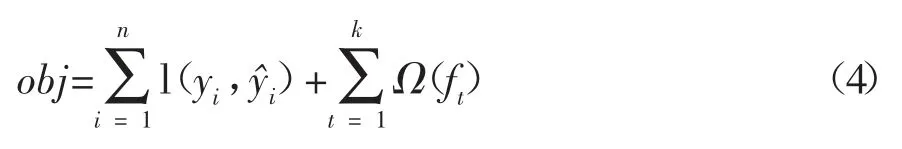
其中Ω为模型的正则项。
以第t步的模型为例,模型对第i个样本xi的预测为:

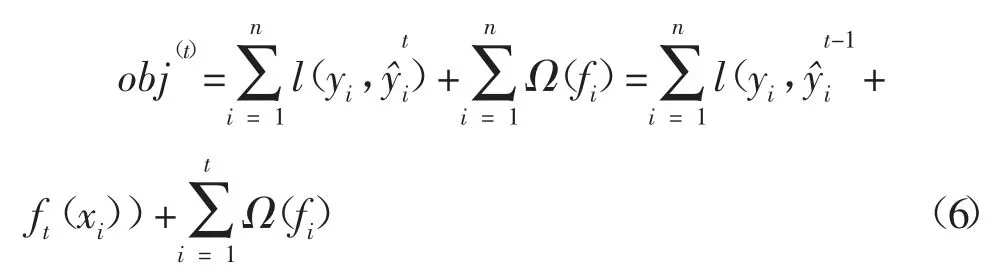
而根据泰勒公式,可以把上述目标函数写为:

其中gi为损失函数的一阶导,hi为损失函数的二阶导。
将决策树定义为ft(x)=wq(x),x为某一样本,q(x)代表该样本所在的叶子结点,而wq则代表叶子结点取值w,所以wq(x)代表每个样本的取值w(即预测值),则目标函数的正则项可以定义为[7]:

其中λ和γ是XGBoost定义的,其值可设定,值越大,表示越希望获得结构简单的树,T为叶子数。

而其中叶子结点j对应的权值可表示为:

所以目标函数可简化为:
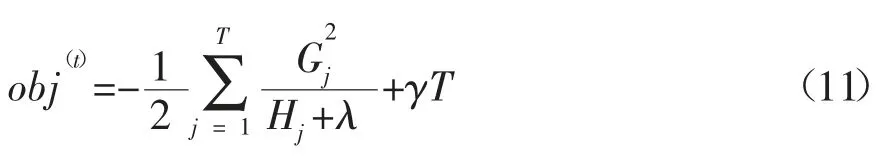
记IL,IR分别是数据集的左右结点,其中I=IL∪IR,则分裂后增益为:
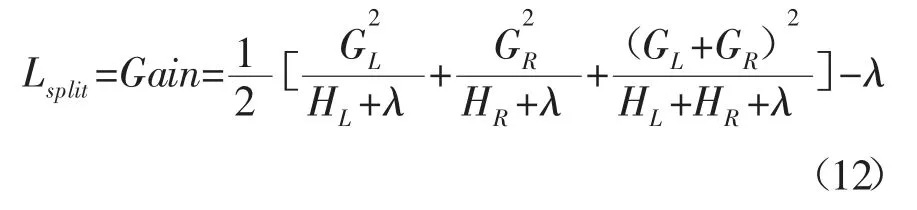
XGBoost在构建树的节点时,为每个节点添加了一个缺省方向,当样本缺失对应特征时,就会被归类到缺省方向上。如果样本存在特征缺失的情况,则只需分配到左右节点而无需遍历,故算法所需遍历的样本量大大减少。稀疏感知算法比basic算法速度快了超过50倍[9-10]。
2.2 模型评价
本文采用均方根对数误差(RMSLE)来作为模型评价的标准。其公式如下:
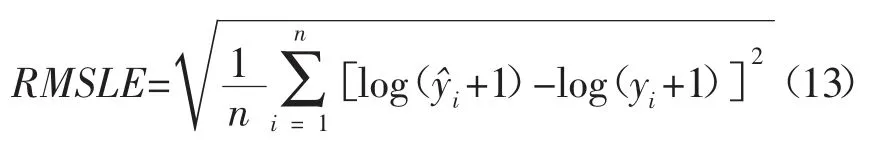
对训练集训练100次后的RMSLE为0.041 646 875 398 8,如图5所示。XGBoost能更好地适应不平衡的数据集,同时也更不容易过拟合,泛化能力较好,应用范围广泛,因此该模型基本可以实现对房价的精准预测。对于该预测模型,可应用到以下场景。
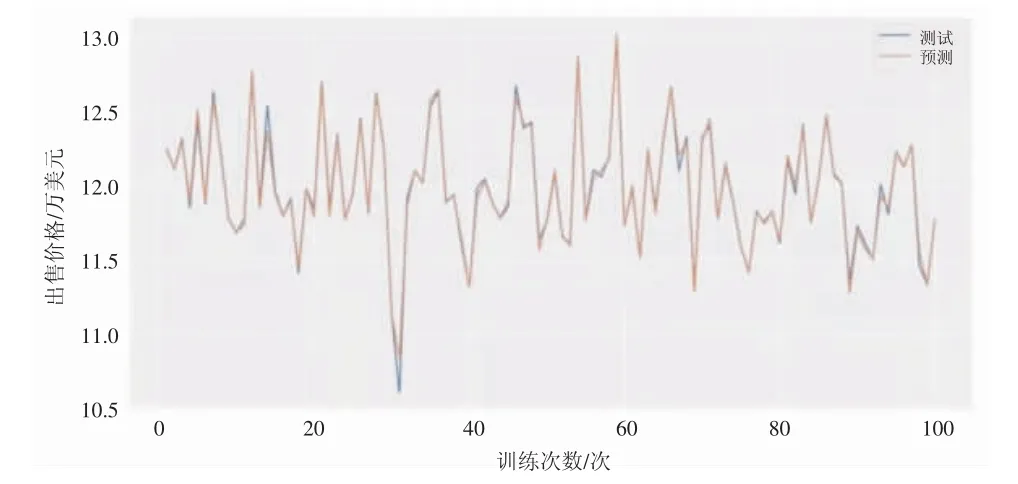
图5 预测结果图
1)链家、安居客等二手房的交易。该模型更加有利于买卖双方看清房价接下来的走势,及时把握住期望成交价格。
2)房产投资的应用。近年来,从《新中产白皮书》中可以看到,新中产人群,除去自住房,投资性房地产占比是最多的。因此,该模型对于投资者有一定的指导性作用。
3 结论
房价预测问题本质上来说就是典型的回归问题。本文基于XGBoost算法进行房价预测,首先对数据进行缺失值处理、相关分析及标准化处理等一系列预处理,然后使用XGBoost算法对数据集进行建模和训练,最终实现对房价的精准预测。
