独柱墩桥梁在偏心荷载作用下的抗倾覆研究
2021-07-07林尚河陈玉骥蓝睿杰
林尚河,陈玉骥,陈 鸿,蓝睿杰
(佛山科学技术学院,广东 佛山 528225)
1 研究背景和意义
独柱墩连续梁桥因其空间利用率高、施工便捷度好、结构轻盈雅致等特点被广泛用在城市快速干道或高速公路匝道桥中,由于桥墩的单支承作用导致稳定性不足、抗扭能力弱,尤其是在重载交通的作用下,重车偏载倾覆问题突出[1-2]。近几年发生的桥梁垮塌事故,如无锡市312国道锡港路上跨桥倾覆、津晋高速公路港塘收费站匝道桥坍塌、浙江上虞立交桥事故等,均为超载车辆偏载引起的独柱墩桥梁垮塌的重大安全事故[3]。可见,独柱墩桥梁有单台或多台严重超载的大型货车同时短间距行驶在桥梁同一侧、同一条车道的极端工况下,桥梁存在倾覆危险。
随着我国交通事业的发展,公路车辆大型化、重载化已成为发展趋势,而目前对独柱墩梁桥倾覆问题的研究主要集中在正常运营状态下车辆荷载引起的倾覆问题,对严重超载车辆等特殊荷载作用下的倾覆问题研究较少。基于以上原因,本项目针对独柱墩桥梁结构的倾覆问题开展研究,以探索能提升独柱墩高架桥服役能力的新型结构型式。
2 结构选型
2.1 研究的主要内容
本项目依托结构设计创新和实践平台,模拟独柱墩桥梁桥面上单侧行车的情况开展研究,通过有限元建立梁板结构模型,分析桥梁的支座反力,从而达到使模型除能承受自身的自重外还可承受一定偏心荷载的目的,进而找到造成独柱墩桥梁倾覆的原因。用Auto CAD画出2种方案的带支座横截面图(见图1),运用Midas Civil进行有限元模型分析,并结合相关力学理论对其进行数据分析,在理论上比较2种方案的倾覆特点及规律。
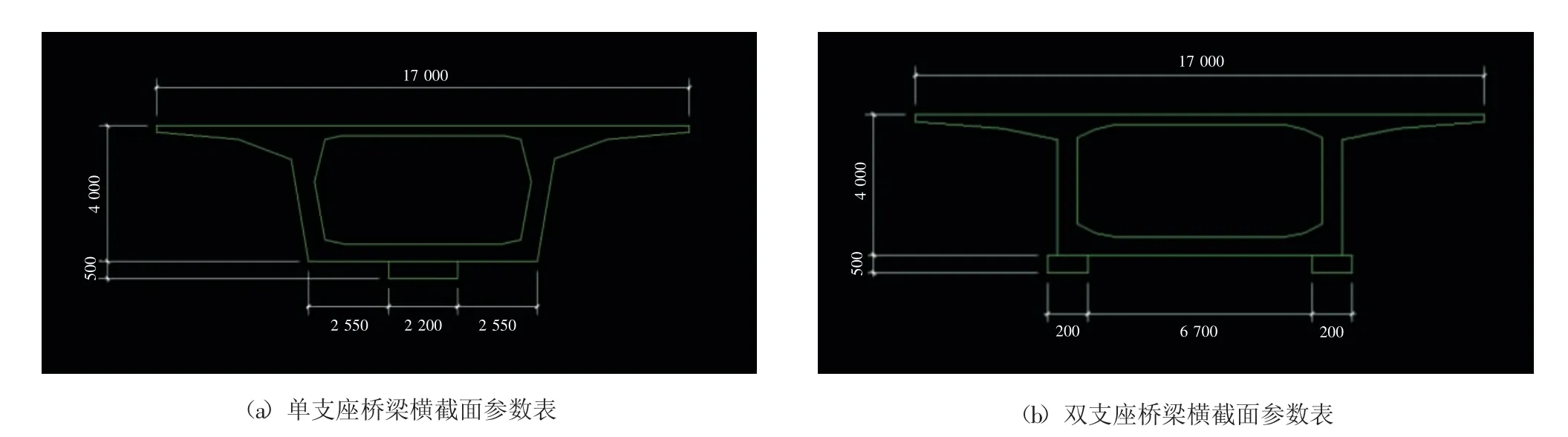
图1 模型横截面示意图(mm)
2.2 计算说明
此次研究所模拟的汽车尺寸为车长6.8 m,宽1.8 m。通过Midas Civil输入荷载、设置边界条件、运行分析,可得出各支座反力的数值,将汽车4个轮子底下的节点为加载点施加节点荷载并进行偏心加载,通过观察各支座是否出现脱空现象(即支座反力≤0,反力以竖直向上为正)来判断桥梁倾覆。
3 结构建模
3.1 Midas模型建立
利用Midas对模型计算分析,在建立模型前需要对模型的材料、节点、单元进行定义,最终建立的单、双支座局部模型见图2~图3。桥梁梁板材料定义时,参数见表1。建模时所有的节点均为刚性节点。2个方案模型支座底下均采用固定铰支座约。

表1 材料参数表

图2 移轴前的节点荷载(N为汽车荷载,G为桥梁自重)
3.2 施加荷载说明
根据《公路工程技术标准JTG B01—2014》规范,汽车荷载可以看作4个节点作用荷载,即模拟汽车4个轮子底下的节点为加载点作节点荷载,分别施加在模型桥面的单侧(见图2,考虑0.5 m护栏)向4个点上,进行偏心加载。但由于Midas的局限性,并不能将实际荷载直接施加在模型桥面单侧,根据等效原则可将单侧的汽车荷载效应分为桥面中心汽车重力N和逆时针力矩My(见图3)。
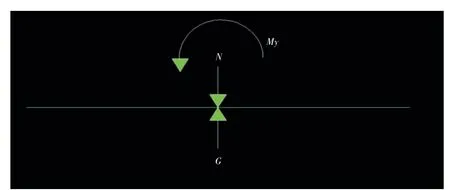
图3 移轴后的节点荷载(N为汽车荷载,G为桥梁自重,My为汽车荷载产生的力矩)
3.3 选型情况对比及数据分析
3.3.1 工况说明
在建立Midas模型时,单、双支座模型施加的约束均在支座下方设置一般支承,支座的上、下节点为弹性连接,且支座上节点与桥梁单元节点为刚性连接(见图4~图5)。
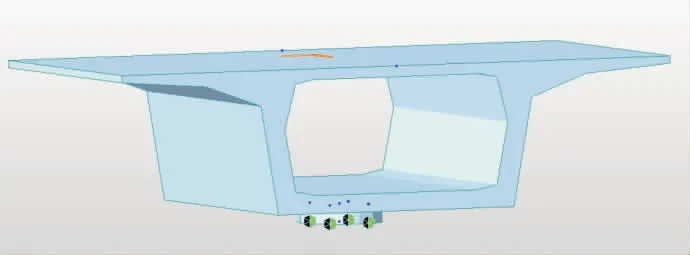
图4 单支座模型及其施加的约束
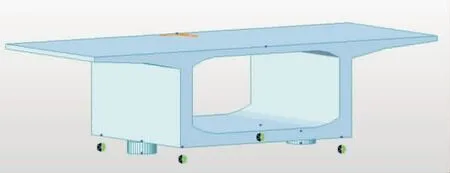
图5 双支座模型及其施加的约束
单支座模型在车辆总质量为5.049 t时,其支座反力为0;双支座模型在车辆总质量为33.77 t时,其支座反力为0。支座反力≤0时即出现支座脱空,最终导致桥梁倾覆,模拟施加荷载及对应的支座反力见表2。

表2 2种模型的模拟施加荷载及对应的支座反力
3.3.2 方案分析对比
通过对两种支座模型施加不同汽车荷载而得到的支座反力数据进行分析,进而对2种支座模型相比较见表3。

表3 2种模型支座反力对比
4 理论计算
4.1 桥梁倾覆的计算理论
桥梁倾覆的案例多发生于单支座独墩桥中,双支座独墩桥几乎不发生倾覆,但为了能更好地通过计算演示桥梁倾覆的过程,计算方法从桥梁双支座的情况考虑,即支座间距>>0。桥梁倾覆计算作如下几点假定:①假定桥梁整体结构并没有发生破坏;②假定墩柱为刚性结构,即EI=∞,EA=∞;③不考虑伸缩缝等构件产生的抵抗弯矩;④取桥体重心为间距的中点处;⑤认为支座1完全脱空时,结构倾覆;设桥梁自重为G,车辆荷载为P,支座1反力为R1,支座2反力为R2,支座间距为L,荷载偏心距为e,重力作用力力臂为L/2。计算简图(见图6)。

图6 计算简图

解得,

由公式(3)~(4)可知,在P增大的过程中,支座1反力不断增大,支座2反力逐渐减小(见图7)。
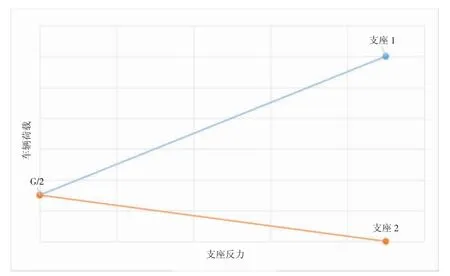
图7 支座1,2反力随车辆荷载的变化线(kN)

当R1=0时,即结构恰好倾覆时,P0为临界荷载,由公式(5)可知,P0与支座间距和偏心距有关,由于偏心距受车辆荷载控制,为不可控因素,因此可以通过适当调宽支座间距加强桥梁抗倾覆的能力。变化趋势(见图8)。
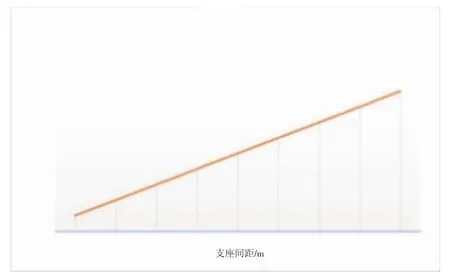
图8 支座间距在抗倾覆中的影响
定义安全系数K=P/P0。当2个支座间距不断缩小直至0,即体系成为单支座结构,可知结构此时只有2个约束为静不定结构,临界荷载为0。然而实际单支座桥梁上L并不为0,而是比较小的一个值,等于支座在横截面方向上的长度,故其仍然存在临界荷载,但是其临界荷载相较于双支座将大大缩减,缩减倍数和L缩减倍数相同。因此单支座的桥梁抗倾覆能力将远小于双支座桥梁抗倾覆能力。
4.2 抗倾覆的理论解决方案及相关计算
由于桥梁的倾覆是桥梁所受倾覆弯矩大于或等于抵抗弯矩所导致的,因此可以通过增大抵抗弯矩来解决这一问题。由于单支座桥梁支座受力较复杂,因此相关可行性通过双支座桥梁说明,即间距远大于支座长度的情况。
设在桥梁横断面右端增加一个竖向约束力。
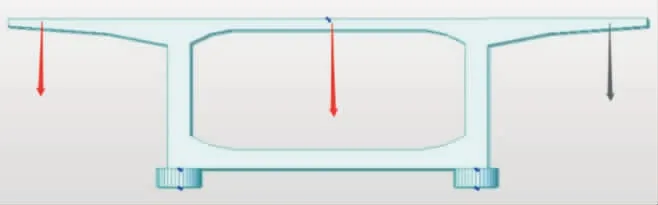
图9 附加约束力示意图
这种约束力方向与支座反力相反,则公式(1)~(2)可改写为公式(6)~(7)式。
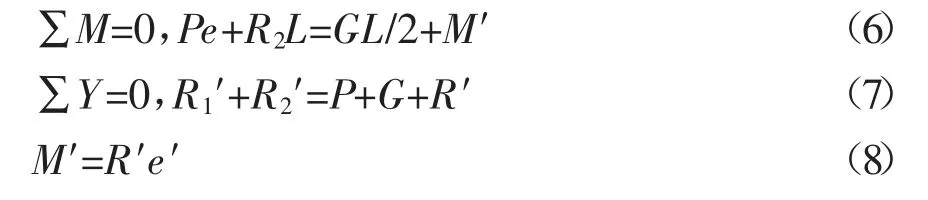
综合(6)~(8)得
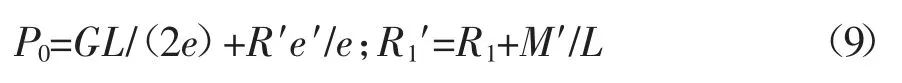

式中:M′为附加抵抗弯矩,kN·m;R′为附加约束力,kN;e′为偏心约束距,m,即附加约束力作用点到支座1的距离;R1′,R2′为加了附加约束力之后的支座反力(kN);其余符号同前。
由于多加了一个约束,方程数目小于未知量数目,体系成为一个超静定结构,解算这个超静定结构如下:
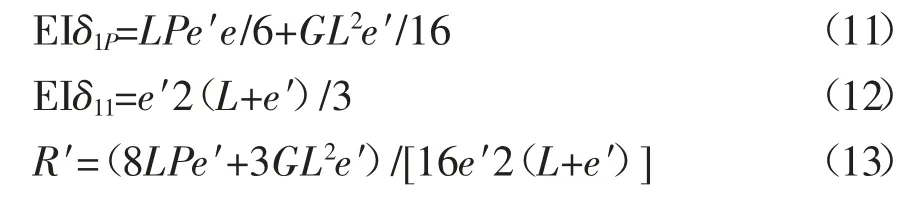
令e=γe′,L=λe′,G=kP,于是:
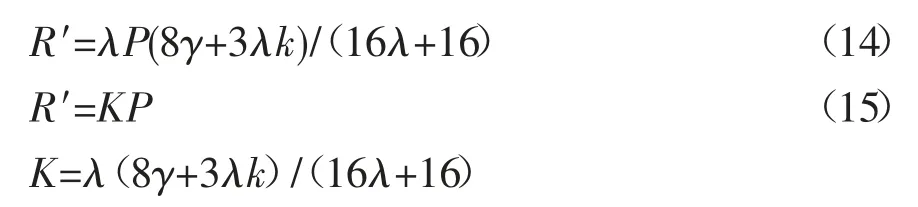
K在同一段桥中为常数,将(15)代入得:

式中:P0′为加约束力之后的临界荷载;其中k可理解为荷载占桥梁自重的比重,λ为偏心距占支座间距的比例,γ为偏心约束距车辆荷载偏心距的比值。由于R′对于桥梁属于外加荷载,希望其值越小越好,由表4可知,3个系数越小,R′越小,对结构就越有利。

表4 各种系数变化对安全系数的影响
方案评估:可以看出临界荷载在加了附加力之后大大增加,由公式(16)看出,临界荷载是未加约束力的(1-K/γ)倍,但是这种抗倾覆措施让支座1的反力大大增加,而对公式(10),由于附加项为负值,支座2的反力减小,这将导致桥梁两支座的反力差异大大增加,使钢筋混凝土的利用率大大降低,并且对支座1附近的RC混凝土抗剪强度要求提高。
方案的实际应用:该外加约束力可由绳索提供,在桥的两端对称安装,安装位置由γ或确定,抗拉强度满足σ≥KR′0/A(K为安全系数,R0′为倾覆时绳索拉力,A为绳索截面积)由公式(15)~(16)得:

5 结语
通过软件有限元分析及理论分析与计算可知,桥梁倾覆临界荷载可以通过在桥两端设置拥有适合抗拉强度和刚度的拉绳来有效提高,但相应带来的不利影响使桥两端支座受力差异变大,即降低了桥梁的工作性能,但是在允许范围内,这种抗倾覆方案仍然具有一定的可行性。
