基于伪曝光融合的快速图像均衡化算法

孙 瑶，杨 硕

(沈阳化工大学 计算机科学与技术学院， 辽宁 沈阳 110142)

直方图均衡化(histogram equalization，HE)是最简单有效的图像增强算法之一，由于速度快，被广泛用于图像处理和预处理中.均衡化算法基于完备的数学理论，但受到离散误差的影响，只是对灰度级进行了适当的拉伸和合并，实际效果取决于原直方图的分布情况.与此类似的是灰度拉伸算法，灰度拉伸对相邻灰度级执行的是等间距拉伸，不进行灰度合并，或仅将超出0或255的灰度级合并.而直方图均衡化后的灰度级间距取决于该灰度级对应的像素数目所占的比例，比例越高，间距越大，比例越小，越容易被合并.这种做法往往更容易被人眼接受，因此，直方图均衡化得到了广泛的应用.

对于直方图呈聚集分布的图像，如，整体偏亮或偏暗的图像，应用直方图均衡化会产生较好的图像增强效果.这类图像经过均衡化后，直方图分布会由聚集变为分散，提高了图像的对比度.而对于存在明显亮部和暗部(光照不均)的图像，均衡化所带来的对比度提升效应则有可能导致过曝和欠曝现象，或者将相邻的灰度级合并，使得图像细节丢失，产生过增强现象.针对经典算法的各种问题，研究人员提出了大量的改进算法.如：文献[1]提出一种根据灰度级间距加权的灰度级合并判定方法，对两个灰度是否合并进行判断，较好地保留了图像的细节；文献[2]在灰度直方图基础上，引入了梯度幅值直方图，分别进行均衡化并迭代融合，改善了经典直方图均衡化细节丢失的问题；文献[3]根据输入图像的平均亮度获得阈值，并自适应修剪直方图，将直方图峰值修剪并移至峰谷处，从而限制了均衡化过程对对比度的增强效果；文献[4]先进行直方图均衡化，再根据人眼对灰度级的分辨能力对截取的部分直方图进行灰度拉伸，提高了算法的保边缘能力.

以上算法属于全局算法，较实用的是限制对比度的直方图均衡化算法(contrast limited adaptive histogram equalization，CLAHE)[5].CLAHE通过对直方图的修剪，改变了灰度级的比例，从而抑制了过度均衡化.基于CLAHE，很多学者提出了改进策略，如：通过插值加快速度[6]，改变为自适应阈值[7]，用拉普拉斯梯度算子增强细节[8]，用伽马矫正提高视觉效果[9].CLAHE改善了全局算法的各种问题，但计算量过大，且未能根本解决过增强的问题.

本文提出一种改进算法，旨在不减弱增强效果的同时，改善过曝和欠曝问题，保留图像细节，以及保持经典HE算法高效的优点.算法受到多曝光融合算法的启发[10-12]，分别对图像的亮部和暗部均衡化，将暗部变亮并将亮部变暗，经过融合后，不仅不会破坏直方图的均匀分布，在空间上，亮度的分布也更加均匀；同时，将方差作为融合系数，防止图像细节丢失.不同于对全幅图像做均衡化处理的全局算法，本算法将处理对象由全局图像变成了被分割后的暗部和亮部两部分图像，分别对亮部和暗部进行均衡化处理，故属于半全局算法.

1 半全局均衡化算法

1.1 直方图分割

算法的流程如图1所示.令I为输入的灰度图像.首先，获得图像的直方图(图1中直方图的横坐标为灰阶，纵坐标为像素的数目)，并在直方图上找到分割中点c，使得左右像素数目相同(接近相同)，将图像分为亮部和暗部.然后，重新分布直方图，以暗部的处理方式为例，具体做法是：将另一半直方图(亮部)平均分布化，即将平均值平均分配给整个灰度阶(0-255)；对于亮部，采用对称的方式处理(如图1).相比图2中CLAHE算法所采用的限制对比度的直方图处理方式，本文的做法实际上略微增强了对比度，均衡化后的暗部和亮部图像记为Il和Ih.

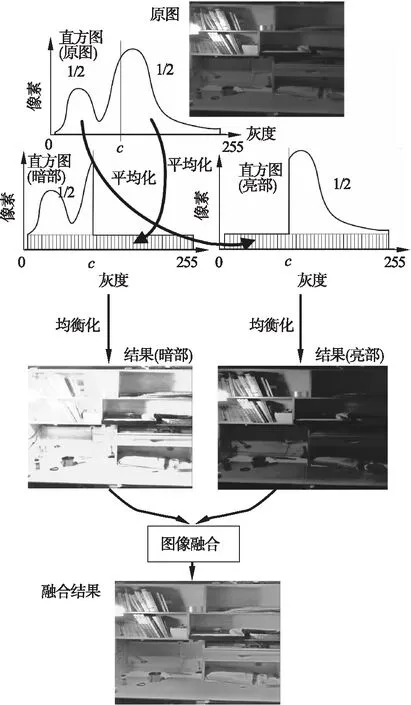
图1 算法处理流程Fig.1 Algorithm processing flow

图2 限制对比度的直方图均衡化原理(CLAHE)Fig.2 Contrast limited adaptive histogram equalization(CLAHE)

对图像的暗部进行直方图均衡化，可以拉伸直方图的低值部分，避免了经典直方图均衡化对直方图低值部分的压缩带来的欠曝光现象；同理，对亮部进行均衡化可以避免过曝问题.

1.2 图像融合

图像融合过程是将经过直方图均衡化的暗部和亮部图像合成为最终结果的过程.由于暗部和亮部均来自于同一图像，因此，算法属于伪曝光融合.融合公式为

O(i)=Tl(i)×Il(i)+Th(i)×Ih(i).

(1)

其中：

式(1)中:Il和Ih分别为均衡化后的暗部和亮部图像；Tl和Th为对应的归一化融合系数；O为融合输出.融合系数由归一化的权重A和B组成，其中A为归一化的分割权重，B为归一化的方差权重；H为分割权重，E为方差权重；γ为方差权重在融合系数中所占的比例，该系数决定了细节保留程度，过小会导致细节模糊，过大则会引入噪声或产生伪边界效果，经实验，一般取1.0到5.0可以获得较好的效果.获取权重H和E是算法的关键.

1.3 分割权重H的获取

分割权重H表示在融合过程中的固有系数，分为暗部权重Hl和亮部权重Hh.其原理是：对于输入图像I在i位置处的像素值e，如果e小于分割点c，则Hl(i)应大于Hh(i)，表示在融合的时候用暗部图像Il多一些；反之，Hl(i)应小于Hh(i)，则在融合的时候用亮部图像Ih多一些.Hl和Hh要根据图像像素值e和分割点c获取.

(2)

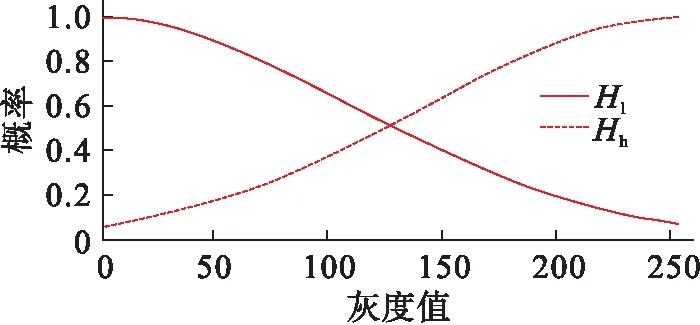
图3 Hl和Hh对应的指数函数Fig.3 Exponential functions corresponding to Hl and Hh

图4为图1中示例图像的暗部分割系数Hl和亮部分割系数Hh，越亮表示权重越大.

图4 Hl和HhFig.4 Hl and Hh

1.4 方差权重E的获取

图像的局部方差能够反映图像的细节，融合过程中，应选取暗部图像和亮部图像中细节较多的部分.方差可以由积分图快速获取.

(3)

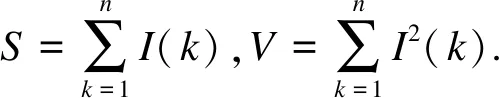
式(3)中，E(i)为图像在i(i={x，y})位置处的局部方差；S和V可以通过积分图快速获取；n=W×W，W为窗口尺度.这里使用多尺度窗口计算方差，获得图像细节，避免图像均匀区域方差无法获取和融合不平滑的现象.具体算法如下.

算法1：方差权重的获取算法

输入：均衡化后的暗部图像Il或亮部图像Ih，大小为w×h;令Wmax为w和h的较大者;令N为保存方差的计算次数.

forW=5 toWmax/2 do

生成窗口{W，W};

fori=0 tow×hdo

if窗口超出图像尺寸then

continue;

else

E(i)=E(i)+式(3)的方差值;

N(i)=N(i)+1;

endif

endfor

endfor

E=E/N;

算法1中，窗口尺度W从5开始增加到Wmax/2，其增量可以采用绝对增量(如：1、2…)或相对增量(如：是上一个窗口的1.5倍或2倍等).使用小的绝对增量可以使权重平滑，但需要较大的计算量，一般情况下可以使用相对增量获得效率和效果的平衡.图5为算法1得到的El和Eh，使用的增量为1.5倍相对增量.像素越亮表示权重越大.

图5 El和EhFig.5 El and Eh

2 实验和结果分析

为了保证算法的运行效率，使用了OpenCV计算机视觉库.算法实现的软件环境为：Windows 7.0+QT 5.9.2+OpenCV3.3.1；硬件环境为：Intel Core I3 3110M(2.4GHz)+8GB内存.对比算法有：HE、CLAHE[6]和二维伽马矫正[13].对比的指标有全局方差Eg、平均梯度值Gavg和平均梯度数量Gn，具体定义为：

(1)全局方差Eg.全局方差主要反映图像在空间上亮度分布的均匀性.为了避免梯度对全局方差计算的影响，计算全局方差前，需要用大尺度的高斯滤波器对图像滤波.

(2)平均梯度值Gavg.用Sobel梯度算子获取梯度幅度绝对值并求平均，该值能够反映算法对细节的保留情况.

(3)平均梯度数量Gn.首先用Sobel梯度算法获取梯度幅值绝对值；然后扫描梯度图像，如果梯度绝对值大于10,将Gn加1；最后将Gn平均化.该值能够反映梯度分布的均匀情况.

部分实验效果如图6～图9所示，图像分辨率均为800×600.

图6 场景1实验对比效果Fig.6 Scenario 1 experiment contrast effect

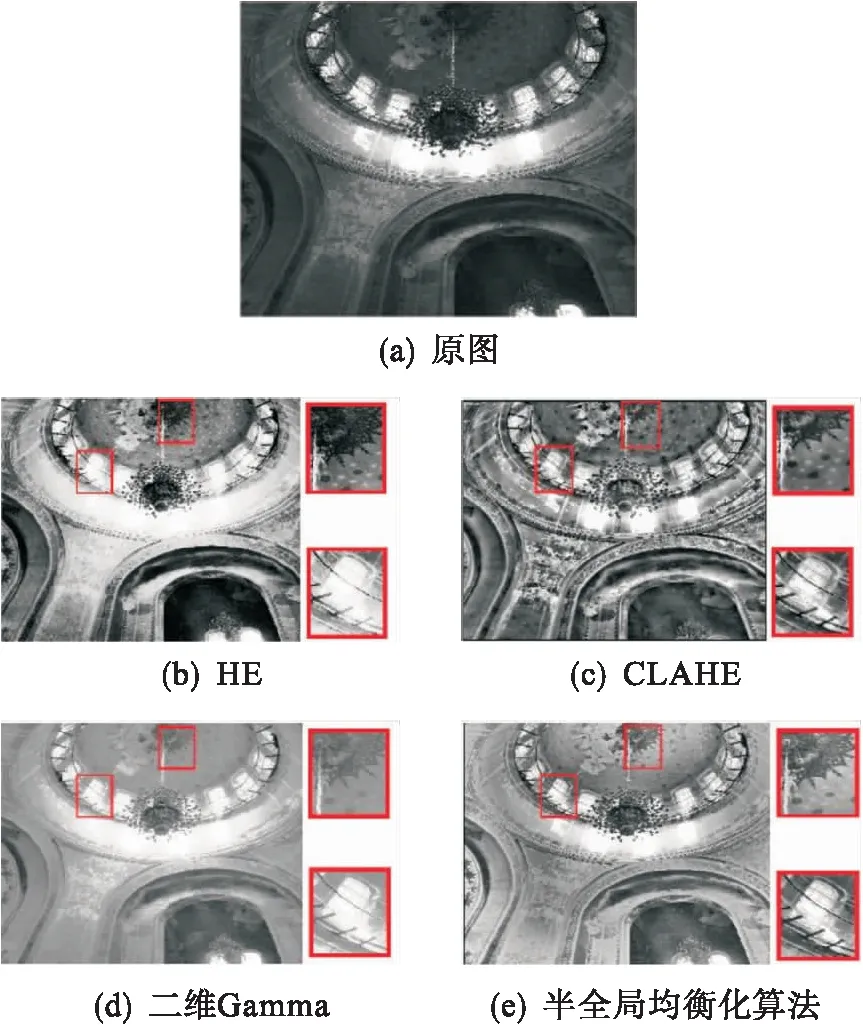
图7 场景2实验对比效果Fig.7 Scenario 2 experiment contrast effect

图8 场景3实验对比效果Fig.8 Scenario 3 experiment contrast effect

图6～图9的4个场景中，从图像局部可以看出：HE算法均产生了过曝和欠曝现象；CLAHE 是局部算法，对细节保留最好，但存在明显的过增强现象；二维Gamma算法处理后的图像较柔和，但图像增强效果不足，对图像细节的保留效果也一般；半全局均衡化算法处理的结果具有较好的主观视觉效果，整体亮度均匀，没有发生过曝和欠曝现象，对细节的保留仅次于CLAHE 算法.表1为定量的实验数据.

图9 场景4实验对比效果Fig.9 Scenario 4 experiment contrast effect

表1 对比算法实验数据Table 1 Contrast algorithm experimental data

表1中，全局方差Eg指示出图像整体的均匀程度，这里希望越小越好，从数据上看，半全局均衡化算法表现最好，HE算法增强了图像的对比度，表现最差.平均梯度Gavg应越大越好，对比算法中，CLAHE表现最好，但其梯度有很大一部分来自于对噪声的放大，半全局均衡化算法表现稍差，该项指标虽然能够反映出图像的细节保留程度，但并不一定客观.表1中的Gn值仅记录梯度的数量，能够反映出梯度分布情况，希望越大越好，CLAHE因为对噪声放大的原因，在该项上表现最好，半全局均衡化算法其次.此外，表2 统计了几种对比算法在图6～图9上的平均运行时间，半全局均衡化算法慢于HE算法，但远快于CLAHE算法.半全局均衡化算法最耗时的部分是在算法1中计算多尺度局部方差的过程，实验中将窗口尺度增量设置为1.5倍的相对增量，在800×600的分辨率下需要计算12个尺度，该增量使效果和速度较为平衡.由于流程较少且使用积分图加快了速度，半全局均衡化算法可以在800×600甚至更高的分辨率下实时运行.

表2 处理速度对比Table 2 Processing speed comparison

3 结束语

直方图分布不均是导致图像质量下降的重要原因，直方图均衡化算法对于直方图呈单峰值聚类分布的情况具有较好的效果，但对于光照不均引起的双峰分布的情况容易产生过曝、欠曝和细节丢失的问题.针对这些问题，本文提出了改进的直方图均衡化算法.实验结果证实了所提算法的有效性.由于算法的复杂度较低，算法可以用于视频实时处理，具有较高的实用性.算法进一步研究的方向将集中在：(1)优化直方图初始分割阈值(暗部和亮部的中值c)，该阈值对最终效果有较大的影响，将其固定在中值的做法是否合理还没有得到充分验证；(2)参数的自适应性，实验发现方差权重比例γ对最终结果也会产生影响，因此，有必要在未来的研究中将其改为自适应阈值.