基于先验误差模型的机载高分宽幅DBF-SAR自聚焦算法
2021-07-07鲍悦陈俊宇施天玥毛新华
鲍悦,陈俊宇,施天玥,毛新华, 2,*
1. 南京航空航天大学 电子信息工程学院,南京 210016
2. 南京航空航天大学 雷达成像与微波光子学教育部重点实验室,南京 210016
合成孔径雷达(Synthetic Aperture Radar, SAR)具有全天时、全天候的高分辨成像能力,是一种重要的远程遥感手段。作为一种高分辨率成像雷达,努力提高获取图像的空间分辨率(测绘精度)和空间测绘宽度(测绘效率)始终是SAR不懈追求的目标[1]。对于常规单通道SAR,一方面,为了获得高的方位分辨率,需要系统有较高的多普勒带宽(方位分辨单元大小与多普勒带宽的倒数成正比),从而系统需要具有较高的脉冲重复频率(Pulse Repetition Frequency, PRF);另一方面,为了获得宽的空间测绘带,同时又要避免距离模糊,又需要尽量降低PRF,因此常规单通道SAR往往无法同时实现高分辨率和宽测绘带成像[2-3]。数字波束形成(Digital Beam Forming, DBF) SAR[4-6]采用方位向多个空间通道接收回波信号,在成像处理中利用空域采样弥补时域采样的不足,可等效实现单通道宽波束接收的方位高分辨率功能,从而达到等效增加SAR系统PRF的目的。因此,高分宽幅DBF-SAR可以有效缓解方位高分辨率与距离向宽测绘带之间的矛盾,获取高分宽幅图像,具有重要的军用和民用价值。
然而,仅当DBF-SAR运动参数满足偏置相位中心天线(Displaced Phase Center Antenna, DPCA)条件,即发射相邻两次脉冲期间DBF-SAR平台的飞行距离为相邻天线间距的一半时,空时等效后获取的等效方位向信号为均匀采样。在实际工程应用中,DPCA条件往往很难满足,因此DBF-SAR回波信号往往在方位向呈现周期性非均匀采样的特点,这为成像处理带来了极大困难。常规的处理方法是在成像处理前增加一个额外的预处理重构过程,恢复均匀采样信号的频谱,进而实现精确的高分辨成像[7-9]。
前期工作中我们提出了一种适用于DBF-SAR的改进极坐标格式算法(Polar Format Algorithm, PFA)[10],该算法将周期性非均匀采样信号的重构嵌入在极坐标格式算法的方位重采样过程中,与传统基于时域的重构算法 (如:Spectral-Fit法和时域重构法[11])以及基于多普勒域的算法[12-13](如:数字波束形成算法等)相比,无需引入额外的运算量,因此具有更好的计算效率。
尽管如此,上述成像算法获取高分辨率图像都存在一个基本假设,即各通道数据得到较好的均衡与校准,同时成像采用的几何参数都是精确已知的。实际上,由于通道硬件、设备噪声、环境等因素的影响,各个通道的幅相特性不可能完全一致。受制造工艺、运动传感器测量精度有限等因素的影响,机载DBF-SAR采样几何参数也不可避免地会存在误差,最典型的误差包括雷达平台飞行速度误差和多通道相位中心间隔误差等。通道间幅相误差与相位中心间距误差会引入周期性的相位误差,而平台速度误差主要在回波相位中引入一个额外的低频二次相位误差。对于这些误差,如果成像时不加以估计和补偿,成像结果将出现成对回波及散焦现象,严重影响SAR成像质量。对于多通道幅相误差的校正,可以通过内校正和外校正等算法实现,目前也已有很多相关报道[14-16]。但对于多通道DBF-SAR采样位置误差的分析和补偿,目前还很少见有相关公开报道,为了弥补这一缺陷,因此本文主要关注该类误差的估计和补偿。
为了提高雷达成像的聚焦精度,可以从回波数据中估计相位误差参数并进行补偿,从而实现目标的重聚焦,这一过程称为自聚焦。传统的SAR自聚焦算法可以分为参数类算法和非参数类算法。参数类算法,如子孔径相关法(Map Drift,MD)、多子孔径相关法(Multi Aperture Mapdrift,MAM)和相位差法(Phase Difference,PD)[17]主要利用相位误差可用有限项多项式表示这一假设,将相位误差的估计问题转变成对多项式系数的估计,该类算法可高精度估计低阶相位误差,但无法估计复杂的高阶相位误差;非参数类算法理论上对相位误差模型没有限制,但实际应用时对图像特征有限制,如在实际SAR中得到广泛应用的相位梯度自聚焦算法(Phase Gradient Algorithm, PGA)[18],由于处理过程中需要对强点目标信号进行加窗,因此也难以估计周期性相位误差。近年来得到广泛研究的另一类算法是基于图像质量指标的最优化算法[19-20], (如最小熵准则自聚焦、对比度最优准则自聚焦),它们通过选择合适的代价函数,对误差进行逐脉冲估计。这类算法由于要在高维空间中搜索未知参数,流程通常较为复杂、计算效率通常非常低。德国宇航局提出在场景中放置定标器[21],引入参考点目标的先验信息,提高了搜索算法的运算速度。然而,对定标器的依赖导致该算法也不适用于一般的应用场景。因此,在已有的自聚焦算法中,还没有一种算法能够完美地解决DBF-SAR中周期性相位误差的高效精确估计和补偿问题。
为解决上述问题,本文提出通过引入误差相位的先验数学结构模型信息,极大降低未知误差参数的维数,从而改善自聚焦参数估计精度和计算效率。经过分析,得到了DBF-SAR图像残留相位误差的解析结构模型,根据该模型,可知残留相位主要包含周期性跳变的高频误差和二次相位误差,其中周期性误差主要导致图像产生重影,而二次相位主要导致目标主瓣展宽,降低分辨率。针对这两种误差,分别采用估计和补偿的策略。首先,利用高频相位误差先验模型,将相位误差逐脉冲估计问题转化为对误差模型参数的估计问题,由于模型未知参数维数极大地降低,采用基于图像对比度准则的最优化方法可准确、高效地估计出模型参数进而得到高频相位误差;高频误差估计和补偿完成后,对于残留二次相位误差的估计与补偿,利用经典的MD算法来实现。
本文结构安排如下:第1节简要介绍无误差时适用于DBF-SAR改进PFA成像原理;第2节首先分析了存在通道间距误差及机载平台速度误差时, PFA成像处理结果中残留相位误差的先验模型,然后利用该先验模型提出了一种基于对比度准则的自聚焦算法(CO-MD算法);第3节是实验验证与分析,通过对仿真的点目标和面目标DBF-SAR数据进行处理和分析,验证了理论分析的正确性以及所提算法的有效性;最后是本文的总结。
1 DBF-SAR极坐标格式成像处理
1.1 DBF-SAR采样模型
不失一般性,假设N通道DBF-SAR数据采集几何关系如图1所示(以N=3为例)。雷达工作于聚束模式,采用一发多收方式采集信号。假设场景中有一理想点目标P,其空间坐标为(x0,y0)。
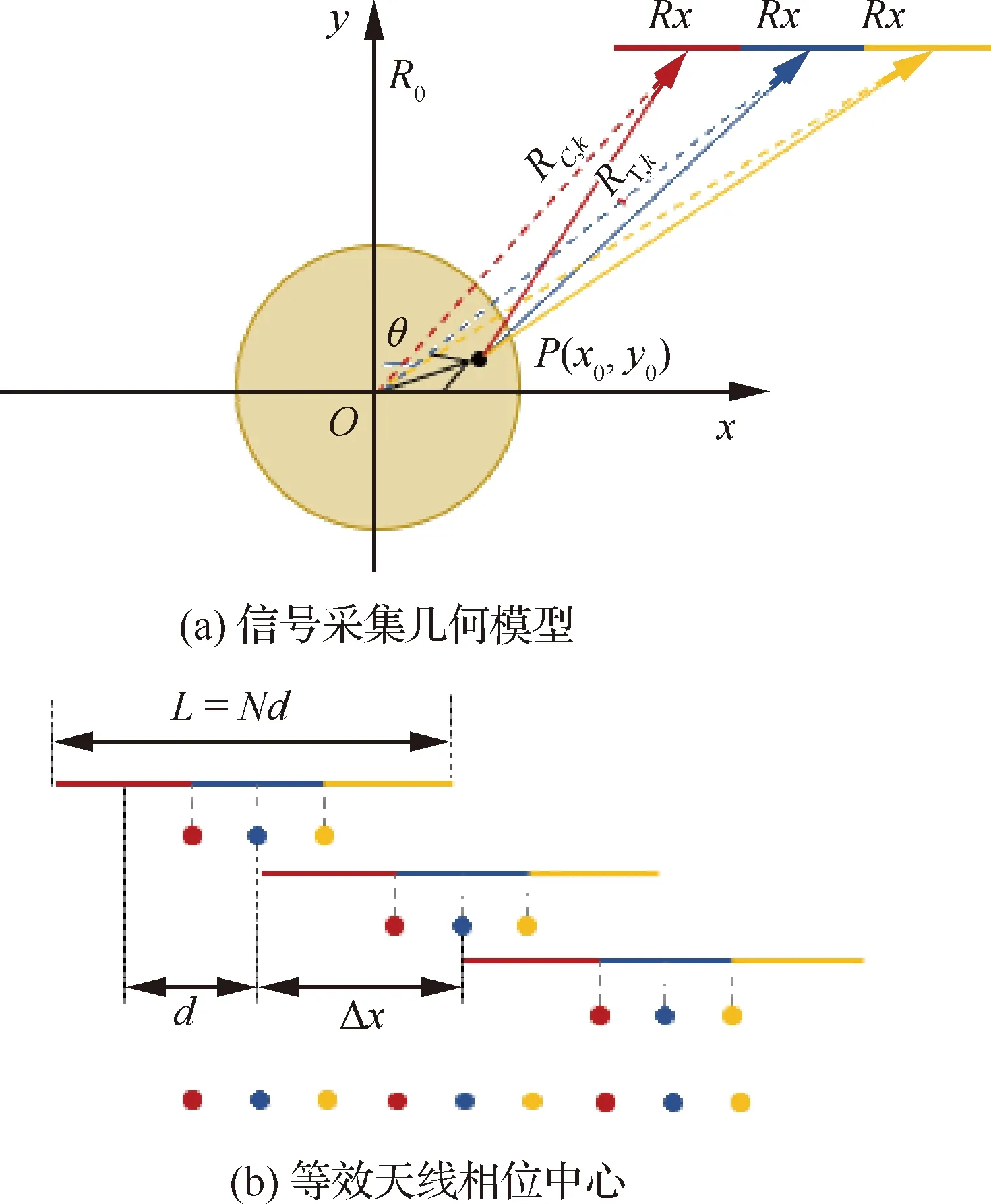
图1 DBF-SAR采样几何关系示意图
DBF-SAR发射天线发射信号由目标反射被第k个子通道接收(M-N+1≤k≤M,M=[N/2])所经过的距离RT,k为
(1)
式中:R0为天线到场景中心的最短斜距;v为雷达平台运动速度;t为方位慢时间;d表示相邻通道相位中心之间的间距。
发射信号通过场景中心反射由第k个子通道接收所经历的距离RC,k可表示为
(2)
式(2)和式(1)中两距离之差ΔRk(t)为
ΔRk(t)=RT,k(t)-RC,k(t)
(3)
而对于传统雷达在方位位置x=kd/2处收发信号,目标与场景中心的双程距离差为

(4)

因此,通道k的回波信号可等效为传统SAR在x=kd/2处的回波信号。为得到均匀采样的方位回波信号,脉冲重复频率为PRF时,发射相邻两次脉冲期间DBF-SAR的飞行距离Δx=v/PRF与天线总长度L=Nd之间应满足Δx=L/2,又称DPCA条件,即
(5)
实际应用中DPCA条件往往很难满足,DBF-SAR方位采样信号大多呈现非均匀采样特性。
1.2 DBF-SAR改进的极坐标格式算法
为了解决DPCA条件不满足时方位信号非均匀采样下的高效成像问题,前期提出了一种改进的极坐标格式算法[9]。新算法将DBF-SAR获取的周期性非均匀采样回波信号重构嵌入到传统PFA方位重采样中,可极大提高运算效率。下面,先简单介绍一下该改进PFA算法原理。
假设SAR发射宽带信号,每一通道接收回波信号经过匹配滤波、运动补偿等预处理后,第k通道的距离频域方位时域信号模型可表示为
(6)
式中:f0为载波频率;fr为距离频率。
在平面波前假设条件下,式(6)中差分距离可近似为:ΔRk(t)=2(x0sinθk+y0cosθk)。由图1几何关系可知,方位角可表示为θk=arctan[(vt+kd/2)/R0]。则式(6)可改写为
(7)
不满足DPCA条件时,DBF-SAR预处理后信号在(t,fr)域呈图2(a)所示非均匀极坐标格式排列。传统极坐标格式算法通过两个一维重采样对该信号进行极坐标格式转换,获取空间频域二维均匀采样信号。其距离向重采样在数学上等效于对距离频率作一个带偏置的尺度变换,方位向重采样在数学上等效于一个Keystone变换[22-24]。不难发现,方位非均匀采样DBF-SAR信号方位向重采样完全可以嵌入传统极坐标格式算法方位向重采样过程,以节约传统算法预处理过程的运算量。为此,提出的适用于高分宽幅DBF-SAR的改进极坐标格式算法原理如图2所示。
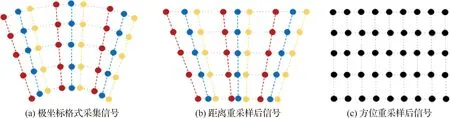
图2 DBF-SAR极坐标格式采样算法原理示意图
首先,对DBF-SAR各通道分别作距离向重采样,在文献[22]中,将这一重采样过程解释为如下的一个距离频率尺度变换:
fr=f0(δr-1)+δrf′r
(8)
式中:δr=1/cosθk,f′r为替换后的距离频率变量。因此,距离重采样后的信号表达式为
(9)
此时信号排列如图2(b)所示。
距离重采样完成后,将各通道数据依据采样位置关系合并,并对合并后的信号在方位向进行重采样,方位重采样等效于做如下变换:
t=f0/(f0+f′r)t′-kd/2v
(10)
式中:t′为替换后的方位时间变量。因此,式(9)经方位重采样变为
(11)
式中:Ω=v/R0。此时,信号排列如图2(c) 所示。可以看到此时采样信号在二维空间频域都是均匀的,因此再对重采样后的信号直接做二维逆傅里叶变换即可得到聚焦的目标图像。
2 高分宽幅DBF-SAR成像自聚焦算法
2.1 DBF-SAR相位误差分析
改进的极坐标格式算法首先通过预处理使场景中心点回波相位为零,获得极坐标格式排列的信号。实际应用中受相邻通道相位中心间距与雷达平台运动速度误差等的影响,改进的PFA对各通道回波信号预处理过程的不精确往往会引入复杂的相位误差,严重降低成像质量[25-26]。
为了获得残留相位误差的先验结构信息,进而改善自聚焦算法效率,首先详细分析了极坐标格式算法对相位误差的作用机理,获得极坐标格式处理图像中残留相位误差的解析结构。在此基础上,通过引入先验误差模型,提出了降维的自聚焦算法,极大地改善自聚焦算法的聚焦精度和计算效率。
2.1.1 DBF-SAR相位历史域误差
在1.2节极坐标格式算法的推导中,假设雷达运动几何参数是精确已知的,而且假设了雷达波前是平面波前。下面,考虑精确的信号模型。相位历史域回波信号可精确建模为
(12)

极坐标格式转换前,先对距离压缩域信号作运动补偿使得场景中心相位为零,参考函数为
(13)

运动补偿后,极坐标格式算法认为的理想差分距离是仅与目标位置x0和y0有关的一次项,其余项均为误差项,不难得到误差项为
(14)
这里,Re=Rr-R,式(14)也可简化为
(15)
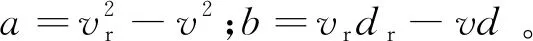
由式(15)可知,DBF-SAR距离向脉冲压缩后的回波信号,经运动补偿相位历史域误差可分为两部分:第1部分是仅与速度有关的二次相位误差,该部分将导致目标点主瓣展宽;第2部分是与通道有关的高频变化相位误差,该部分将导致图像出现重影。
2.1.2 PFA图像残留误差
2.1.1节得到了相位历史域的误差信号模型,但在自聚焦处理时,更关心经极坐标格式转换后的误差信号,因此下面分析极坐标格式转换对误差的影响。
由2.1.1节分析可知,在极坐标格式转换前,精确的二维相位历史域信号为
(16)
极坐标格式转换的第1步是距离向重采样,即对距离频率做尺度变换。将式(8)代入式(16),得到距离重采样后的信号表达式:
(17)
极坐标格式转换的第2步是方位重采样,即对方位时间做如式(10)所示尺度变换,方位重采样后的信号变为
(18)

因此,方位采样时间离散化后的误差信号如式(19)所示:
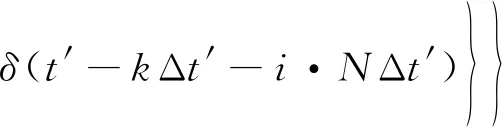
(19)
式中:Δt′为方位重采样后的离散化方位时间采样间隔,Δt′=1/(N·PRF)。
通常,f′r≪f0且θ′→0,残留相位误差导致的距离徙动效应可以忽略不记,假设发射信号波长表示为λ,式(19)可简化为
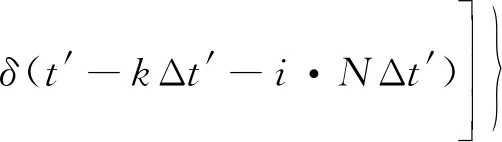
(20)
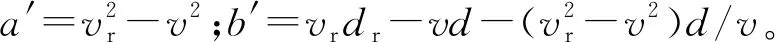
由式(20)可知,残留误差仅与方位时间有关,因此在自聚焦过程中仅需估计和补偿方位相位误差;通过式(20)还可以看到,方位相位误差模型中仅存在两个未知参数a′与b′。未知参数a′对应二次相位误差,导致图像主瓣展宽;未知参数b′对应周期性跳变相位误差。对式(20)第2部分做傅里叶变换可得:
iPRF)kΔt′]·δ(f-kb′/λR0+iPRF)
(21)
由于误差一般较小,b′≪λR0,周期性跳变相位误差将导致图像在k·PRF处产生虚假目标,对方位宽度为totalx的场景,即在k·totalx/N处出现虚假目标;同时该误差还会引起主瓣略微展宽。
仅有相邻通道相位中心间距误差存在时,vr=v,式(20)中a′=0、b′=v(dr-d)≠0,无二次相位误差,存在周期性跳变误差,主要导致虚假目标出现,图像产生重影,降低成像质量。
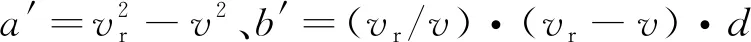
DBF-SAR实际工作过程中,相邻通道相位中心间距与机载平台速度误差往往同时存在,方位相位误差包含一个二次相位误差与呈周期性跳变的误差项,成像结果存在明显的重影,同时目标主瓣展宽严重。因此有效的自聚焦算法必须对二者均进行有效补偿。
2.2 基于先验误差模型的DBF-SAR自聚焦算法
通过2.1节的分析,得到DBF-SAR图像残留相位误差的解析结构模型,根据该模型,知道残留相位主要包含周期性跳变的高频误差和二次相位误差。针对这两种误差,采用分别估计和补偿策略。
对于高频相位误差的估计,考虑到经典的MD和PGA等算法都无法有效估计,提出采用基于图像对比度准则的最优化算法来实现。传统最优化算法采用迭代搜索策略,在误差参数维数较高时计算效率极低。但在本文中,通过推导已经得到了高频相位误差模型,通过引入该误差模型信息,对相位误差参数的估计可以转化为对先验误差模型中少量未知参数的估计,因此实际只需要估计式(20)中的模型未知参数b′。这样采用最优化算法仍可以得到很好的计算效率。
对比度最优自聚焦算法(Contrast Optimization Autofocusing Algorithm,COAA)通过对误差区间内的参数搜索估计相位误差,可以有效估计误差模型中的各项未知参数,实现图像聚焦。
图像对比度有许多不同定义,本文将其定义为图像强度标准差与平均值之比以衡量图像的聚焦深度。聚焦深度越高,图像对比度越大;无相位误差时图像对比度最优,其计算公式为
(22)
式中:I(m,n)为坐标(m,n)像素图像强度。
对二次相位误差的估计,本质上也可以结合在上述最优化算法中通过搜索得到,但扩展参数搜索的维度将极大增加算法运算量。同时,考虑到目前二次相位误差的估计已有更高效的算法,譬如MD和PD等算法都能高效估计二次相位误差,因此这里采用MD算法来估计二次相位误差。
综上,提出的DBF-SAR自聚焦算法处理流程如图3所示。其主要处理步骤包括:
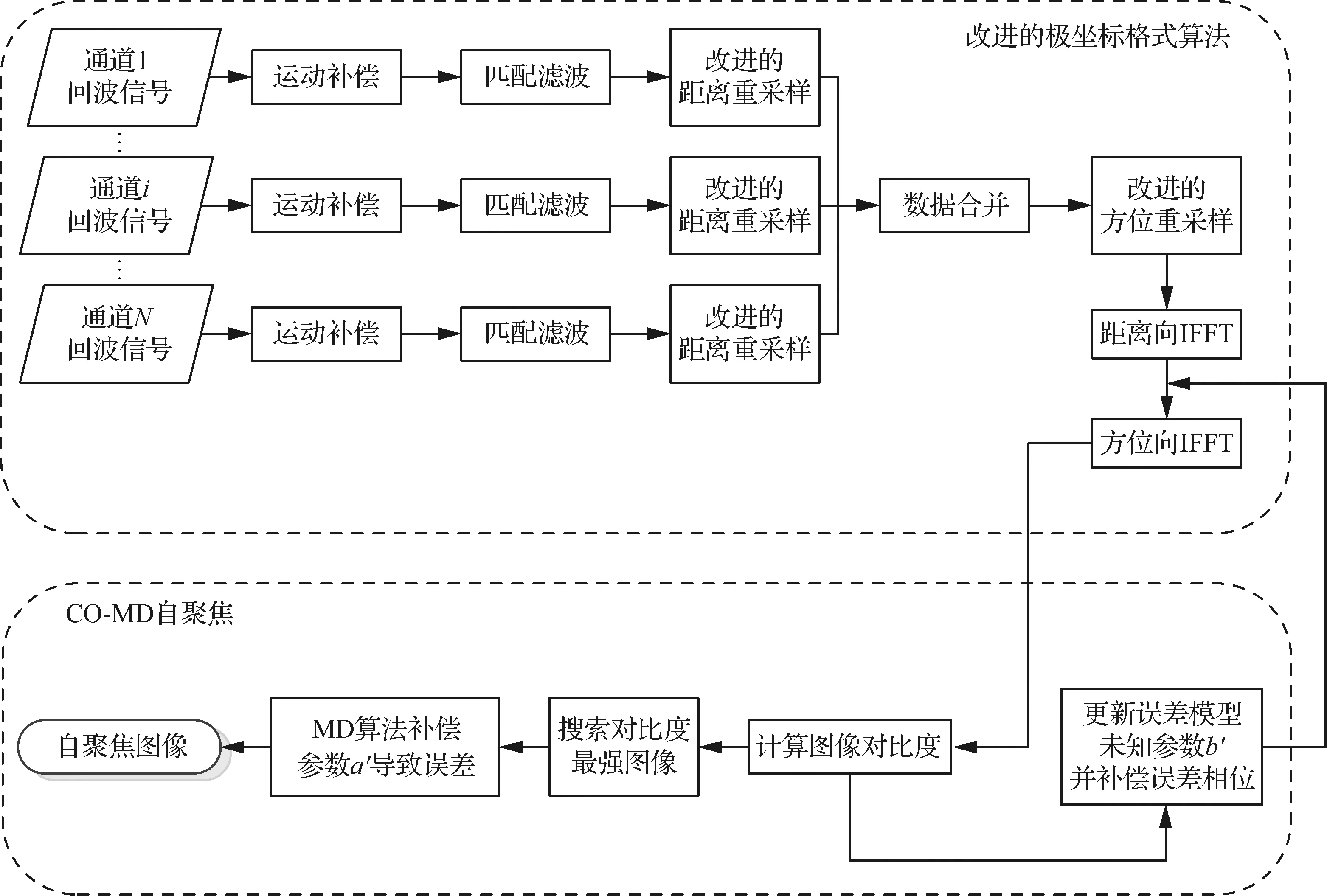
图3 基于误差模型的高分宽幅DBF-SAR自聚焦算法流程图
步骤1基于提供的系统参数,利用适用于高分宽幅DBF-SAR的改进极坐标格式算法实现回波信号的成像处理。
步骤2利用对比度定义式计算成像处理后的DBF-SAR图像对比度。
步骤3将误差模型的未知参数a′设置为0,并根据遍历,更新误差模型中的参数b′,将该值代入式(20)中得到预估相位误差信号,并在距离压缩域进行方位误差相位补偿。
步骤4重复步骤3,直到误差模型参数搜索完毕,提取对比度最强图像。
步骤5对步骤4得到的对比度最强图像,利用MD算法实现二次相位误差的估计和补偿。
3 仿真结果与分析
3.1 点目标仿真
为验证2.1节对DBF-SAR方位相位误差分析结果,分别对仅存在相邻通道相位中心间距误差和仅存在机载平台速度误差的单点目标做仿真分析,点目标所处位置坐标为(0,0) m,方位分辨率为0.27 m,仿真参数如表1所示。
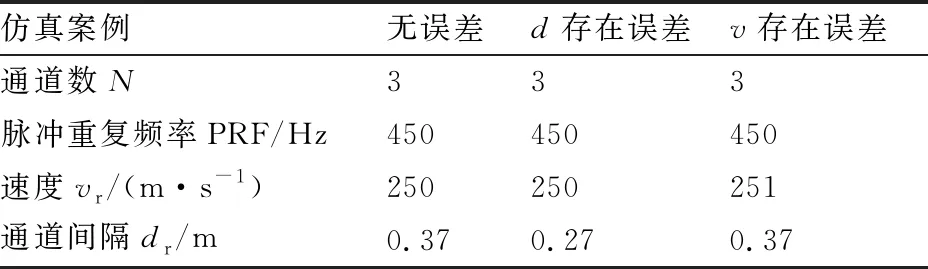
表1 DBF-SAR主要仿真参数
DBF-SAR仅存在相邻通道相位中心间距误差时,其二维重采样后信号的方位相位如图4所示。通道0不存在相位误差,故其相位误差为0;而通道-1及通道1存在符号相反的线性相位误差,三通道数据合并后误差呈现周期性跳变。
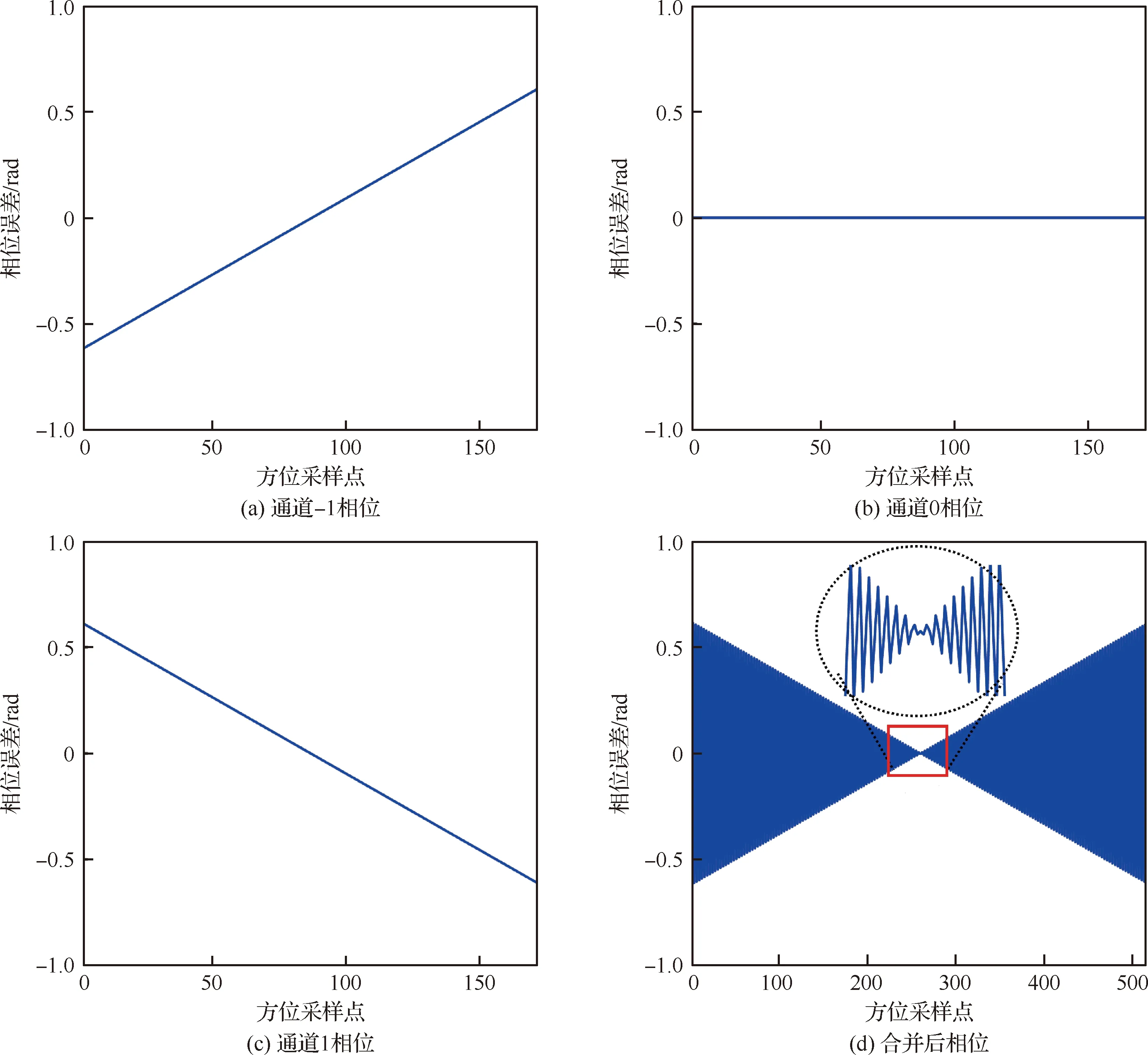
图4 DBF-SAR仅d存在误差时的相位误差
如图5所示,DBF-SAR仅存在速度误差时,二维重采样后信号的方位相位包含二次相位误差,同时也存在周期性跳变误差。3个通道的二次误差项系数均与通道0相同,通道-1与通道1还包含符号相反的线性相位误差,因此3通道数据合并后误差也会呈现出周期性的跳变。
图5 DBF-SAR仅v存在误差时的相位误差
图6实线为无误差时点目标成像结果方位剖面图,虚线为图4信号成像结果方位剖面图。可见相邻通道相位中心间距误差主要导致图像出现虚假目标,成像场景方位向总长度为138.86 m,虚假目标出现在±46.28 m处,与式(21)结论一致。虚假目标导致的重影将严重影响成像质量。图6右上角的局部放大结果中可见点目标主瓣有不明显的展宽,也将降低成像质量,在方位分辨率误差允许的范围内可忽略不计。
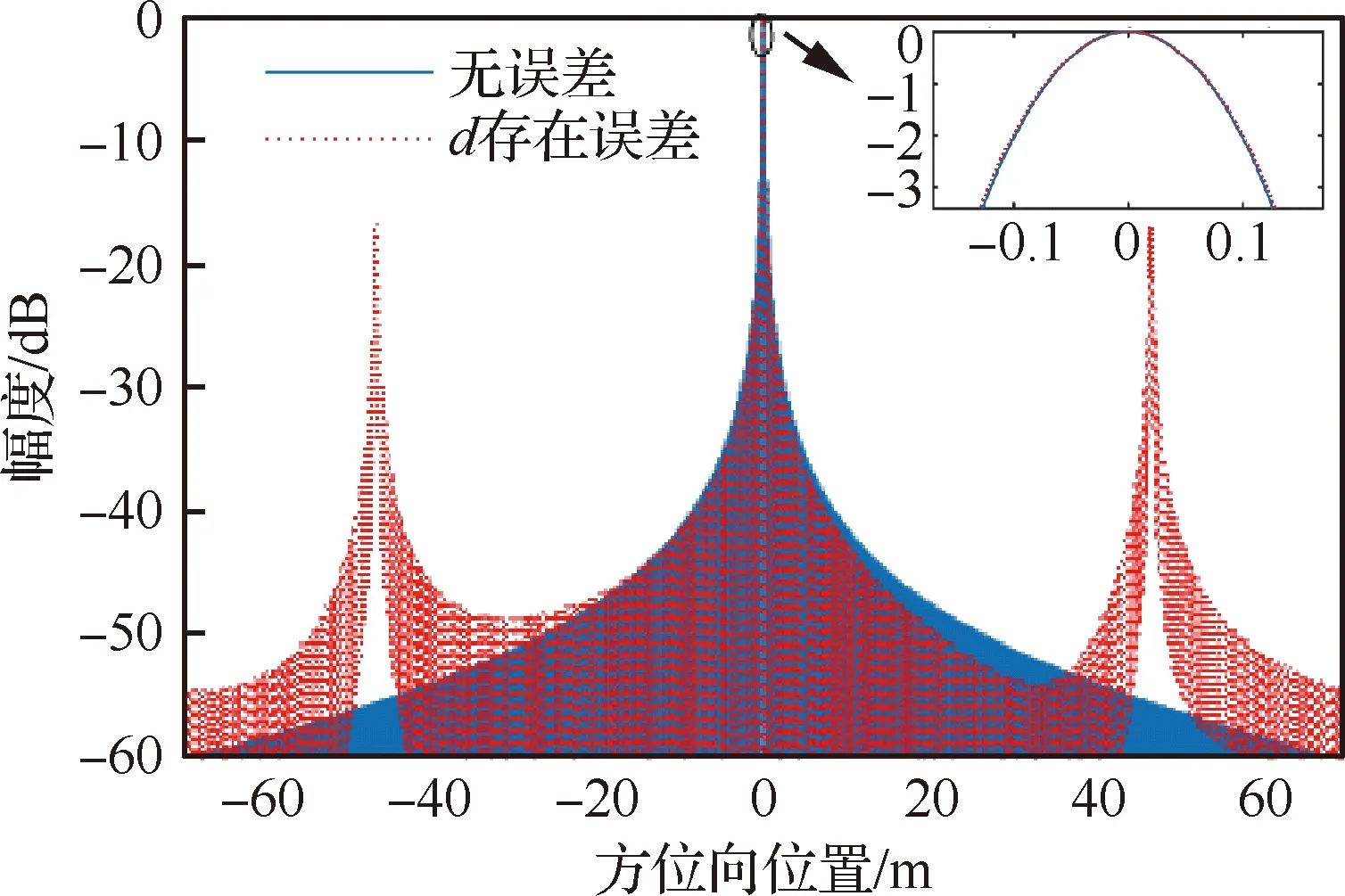
图6 d存在误差时方位剖面对比图
图7虚线为存在速度误差的信号成像结果方位剖面图。可见点目标主瓣有明显的展宽,降低了成像质量,而±46.28 m处的虚假目标幅度很小,对成像质量无明显影响,可不予考虑。
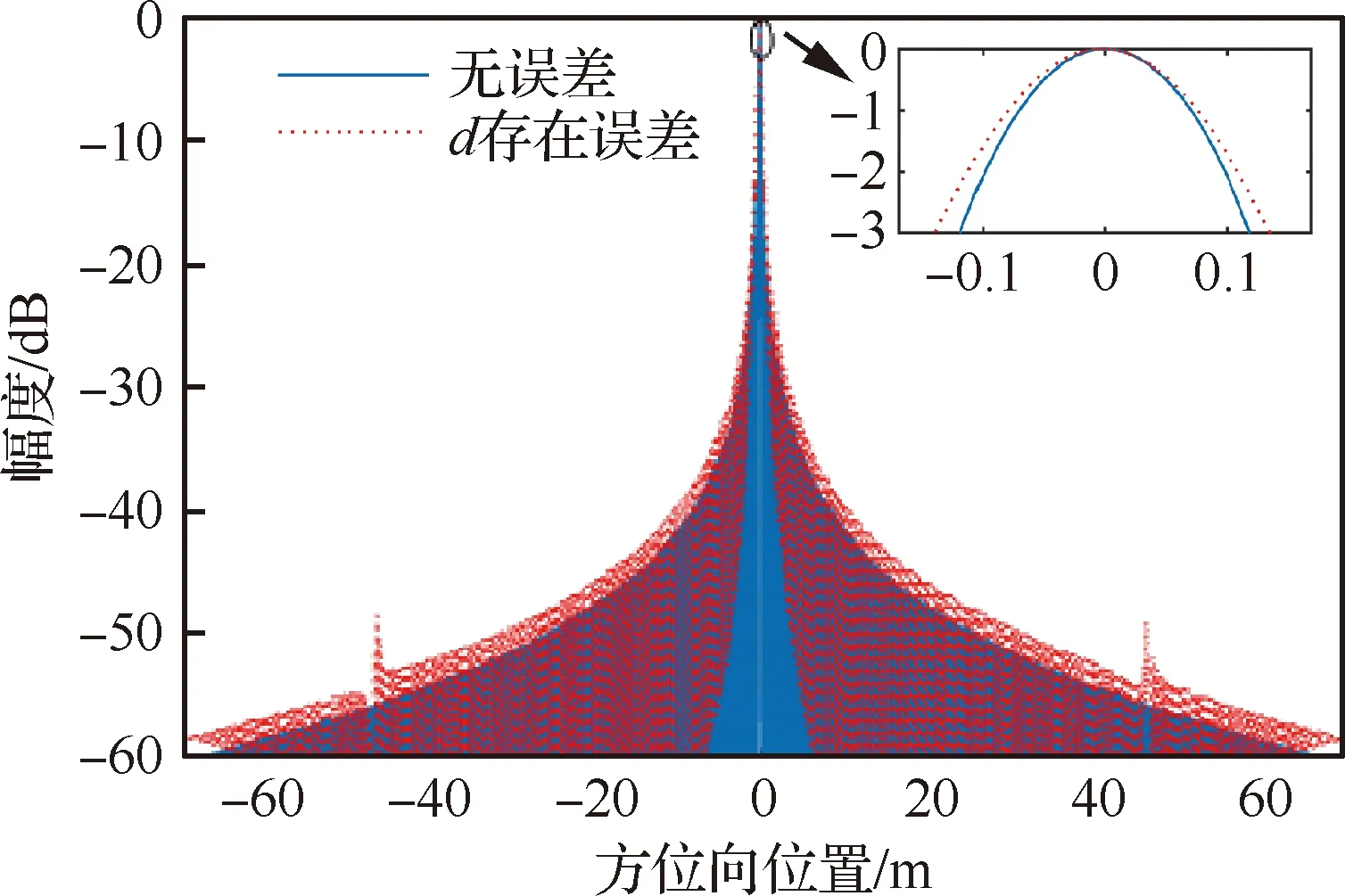
图7 v存在误差时方位剖面对比图
无论何种原因导致的相位误差均会降低DBF-SAR成像质量,图8和图9依次给出相邻通道相位中心间距相对误差、机载平台速度相对误差对DBF-SAR成像指标((a)3 dB宽度、(b)虚假目标幅度)的影响。
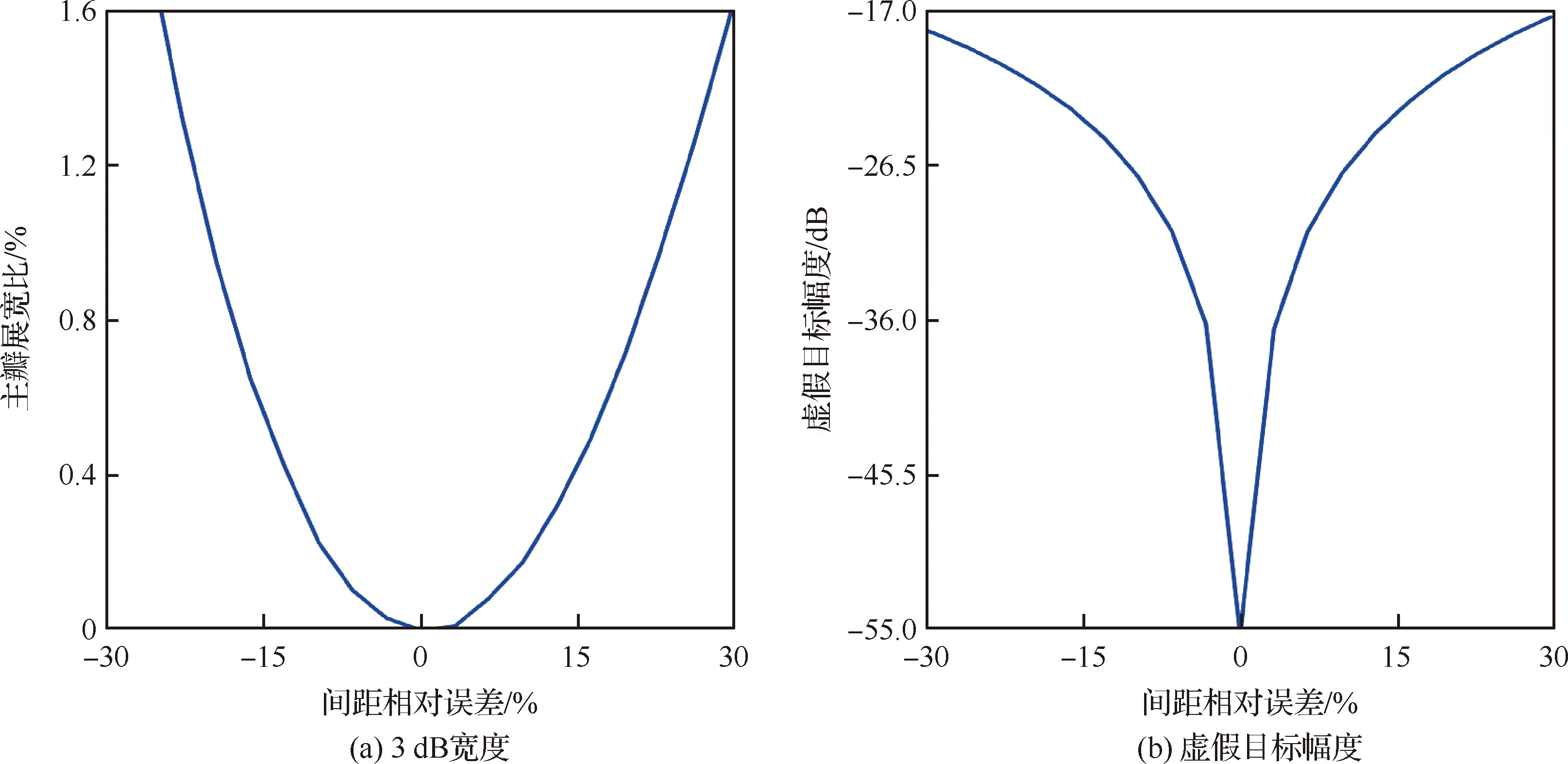
图8 间距相对误差对DBF-SAR成像指标的影响
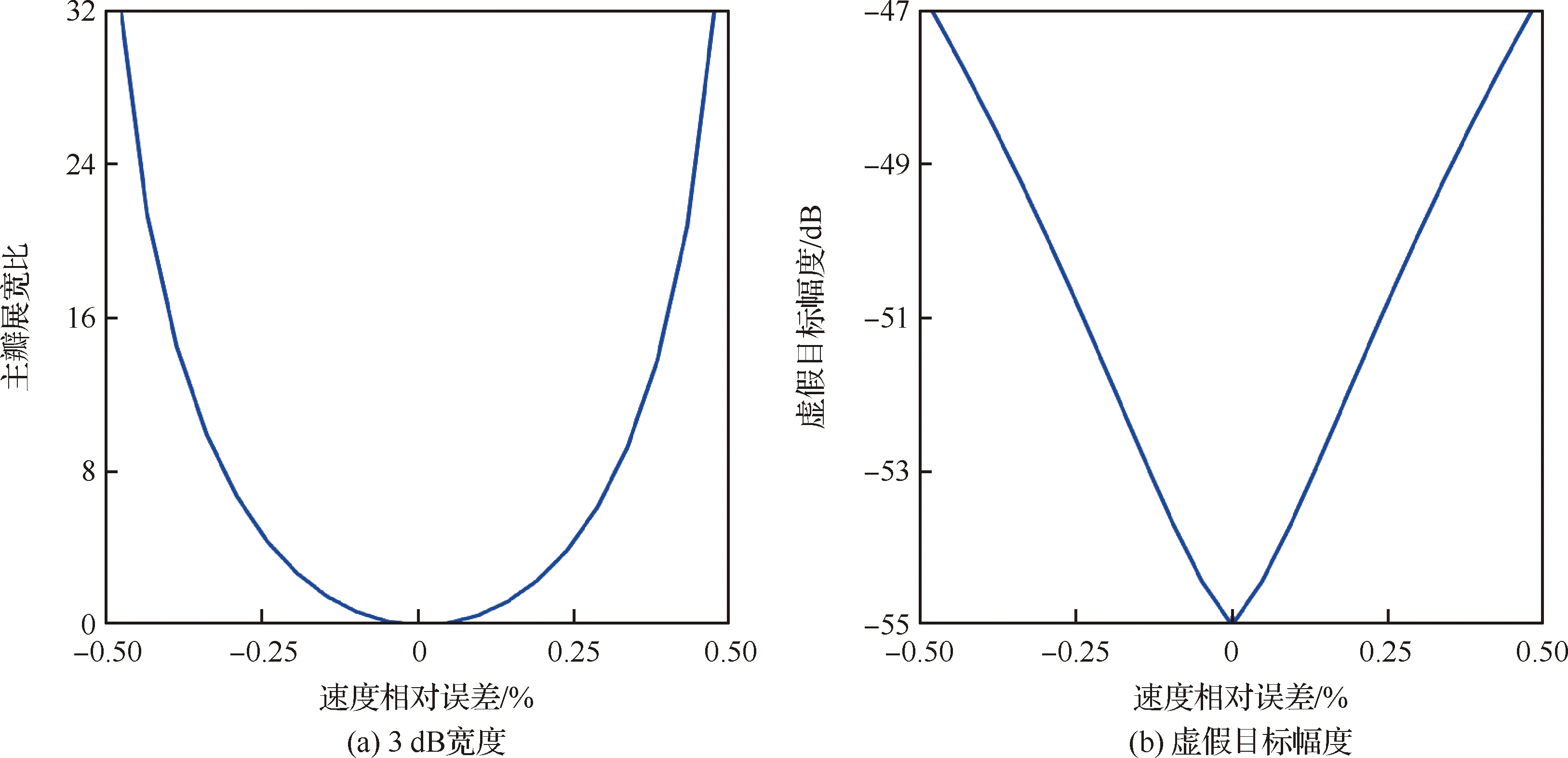
图9 速度相对误差对DBF-SAR成像指标的影响
相邻通道相位中心间距存在0.1 m误差时,相对误差大小为27%,点目标方位向主瓣宽度为0.274 m,相对于0.27 m方位分辨率展宽了1.6%,虚假目标高度为-18 dB;而速度存在1 m/s误差时,相对误差大小为0.4%,主瓣宽度为0.33 m,展宽了25%,其虚假目标高度为-48.7 dB。可见,相邻通道相位中心间距误差主要影响虚假目标幅度,而速度误差对主瓣宽度影响更为明显。
3.2 面目标仿真
为验证2.2节提出的CO-MD自聚焦算法在成像处理中的有效性,给出无误差与存在不同误差时,成像处理结果对比图。由于缺乏DBF-SAR实测数据,实验中通过对某单通道SAR实测回波数据进行处理来模拟得到多通道信号:首先对获取的信号进行方位升采样,再依据采样点与DBF-SAR等效采样相位中心的对应关系,获取方位向非均匀采样的3通道DBF-SAR回波信号。
雷达发射信号带宽为150 MHz,对应距离向理论分辨率为1 m,方位理论分辨率约0.27 m。构造的多通道SAR不满足DPCA条件,相邻通道间隔为0.37 m,雷达做直线运动,速度为250 m/s。
无误差条件下,方位非均匀采样的两通道DBF-SAR改进极坐标格式算法成像结果如图10所示。图像中(9.5,-170) m处的孤立强点目标局部放大后,可见改进的PFA有效实现了成像,该图像对比度为13.256 3。

图10 无误差成像结果
存在相邻通道相位中心间距、机载平台速度误差时,DBF-SAR采集上述场景回波信号经改进PFA成像,图像对比度将会降低。相邻通道相位中心间距相对误差、机载平台速度相对误差与图像对比度的关系如图11所示。由图可知,相邻通道相位中心间距误差与机载平台速度误差均会导致图像对比度下降,因此可将图像对比度作为代价函数,搜索误差模型中的误差参数,实现图像自聚焦。
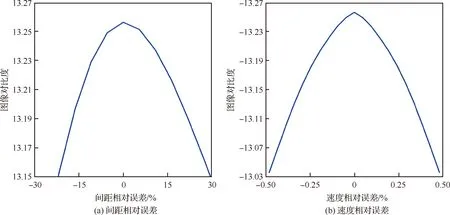
图11 相对误差与图像对比度关系
3.2.1 存在单一误差成像结果
由2.2节推导的误差模型分析知,相邻通道相位中心间距误差主要影响图像虚假目标幅度,对目标主瓣宽度影响不大。图12(a)给出相邻通道相位中心间距存在0.1 m误差时的成像结果,图中可明显观察到成像结果A区域分别在A1与A2区域内形成的重影,无法区分重影与实际目标,该图像对比度为13.250 3。由(9.5,-170) m处点目标的局部放大图像可知,点目标无明显的主瓣展宽,呈现的结果与2.2节理论分析一致。

图12 存在单一误差时DBF-SAR成像及误差补偿结果
当仅存在相邻通道相位中心间距误差时,以图像对比度为代价函数,通过对参数b′的搜索,可以得到误差补偿函数。图12(b)为相邻通道相位中心间距误差补偿后的图像,其图像对比度为 13.256 1,近似等于无误差图像对比度。图像中的重影问题已经得到解决,虚假目标得到抑制,同时(9.5,-170) m处点目标成像效果良好,基于对比度的参数搜索误差补偿可明显改善图像质量。
机载平台速度误差主要导致点目标主瓣展宽,不会产生较为明显的虚假目标。图12(c)给出速度存在5 m/s误差时的成像结果,图像模糊,无明显的重影问题,图像对比度为11.7876。由 (9.5,-170) m处点目标的局部放大图像可见,主瓣存在明显展宽,与2.2节理论分析结果也保持一致。通过MD算法补偿二次相位误差,可以得到如图12(d)所示聚焦好的图像,点目标放大结果显示方位向主瓣展宽问题得到解决。MD算法可以有效提高存在速度误差的图像质量。
3.2.2 误差同时存在成像结果
机载平台速度与相邻通道相位中心间距均存在误差时,图像会出现严重散焦与明显重影,如图13(a)所示(相邻通道相位中心间距误差为0.1 m,机载平台速度误差5 m/s),图像对比度为11.695 6,图像质量明显下降。
图像出现了明显重影,如图中A区域在A2区域内有明显重影,同时 (9.5,-170) m处孤立强点的放大结果可观察到明显的主瓣展宽。直接利用MD算法对其进行自聚焦成像,结果如图13(b)所示,主瓣展宽问题已被完全解决,但A区域在A1、A2区域仍存在明显的重影。
通过图3所示基于先验误差模型的高分宽幅DBF-SAR自聚焦算法流程,首先搜索使得图像对比度最优的DBF-SAR误差信号模型的参数b′,方位向周期性的跳变误差得以补偿,重影消失,其结果如图13(c)所示,图像对比度为11.736 9。
接着,利用MD算法补偿二次相位,即可有效实现图像的自聚焦,其结果如图13(d)所示,相位误差被完全补偿,点目标放大结果显示散焦及虚假目标问题均被解决,图像对比度为13.255 8。
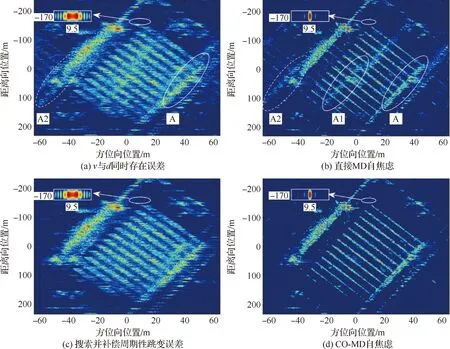
图13 同时存在速度与间距误差时DBF-SAR成像及误差补偿结果
4 结 论
本文针对高分宽幅DBF-SAR信号采集过程存在误差的问题,提出了一种基于先验误差模型的自聚焦算法。主要结论如下:
1) 推导改进的PFA成像处理后DBF-SAR由相邻通道相位中心间距与机载平台速度误差引入的方位相位误差解析模型,并通过点目标仿真深入分析相位误差对成像结果的影响。
2) 算法基于图像最大对比度准则,突破传统自聚焦算法对误差形式的限制,将误差搜索问题转化为先验误差模型中的未知参数搜索,有效解决误差导致的图像重影与散焦的问题。
3) 统一不同误差因素所导致的方位周期性跳变相位误差的形式,简化了误差模型。
4) 利用基于误差模型的MD自聚焦算法估计误差模型中的二次相位误差,降低参数搜索维度,提高了运算效率。
所提算法在诸如MIMO雷达、相控阵雷达等多通道雷达成像信号处理领域具有广阔的应用前景。
本文中的误差分析仅考虑了常见的一维速度误差影响,实际系统中,机载SAR平台运动还可能存在三维运动误差。因此,未来工作中将对更复杂模型下的相位误差形式进行进一步分析,为更一般条件下的机载高分宽幅DBF-SAR自聚焦成像提供理论依据。
