HyTRV流场特征与边界层稳定性特征分析

2021-07-07陈坚强涂国华万兵兵袁先旭杨强庄宇向星皓

航空学报 2021年6期

陈坚强，涂国华，万兵兵,*，袁先旭，杨强，庄宇，向星皓

1. 中国空气动力研究与发展中心空气动力学国家重点实验室，绵阳 621000

2. 中国空气动力研究与发展中心计算空气动力研究所，绵阳 621000

3. 中国空气动力研究与发展中心超高速空气动力研究所，绵阳 621000

自20世纪50年代起，高超声速飞行器已成为各航空航天大国的重点关注对象。高超声速飞行器飞行时有失败，比如美国X-15挡风罩破碎和燃料箱支架烧坏、哥伦比亚航天飞机失事、HTV-2飞行试验失败等。为了发展先进的高超声速飞行器，美国在20世纪80年代启动了国家空天飞机(National Aero-Space Plane，NASP)计划，但因缺乏科学的理论指导最终没能成功，不得不转向对简单模型的基础研究，高超声速边界层转捩问题是其中亟需解决的关键问题之一[1]。由于边界层的层流和湍流两个流动状态对飞行器摩擦阻力、噪声、表面热流等方面存在着巨大差异，对飞行器的安全和气动性能具有显著的影响[2-4]。因此，研究高超声速边界层转捩问题，预测层流到湍流的转捩位置，对飞行器的气动设计和热防护设计尤为重要。

一般来说，边界层转捩是由边界层模态失稳导致的，其失稳机制研究已近百年。失稳模态主要包括第一(T-S波)/第二模态、横流失稳模态、流向涡失稳模态、Görtler失稳模态和附着线失稳模态等。对于不同模型，触发转捩的主导模态可能会不一样。第一(T-S波)/第二模态之于无后掠无攻角的平板和锥形等[5-10]；横流失稳模态之于有后掠或有攻角的平板、锥形、机翼等[11-15]；流向涡失稳模态之于一般曲面模型等[16-17]；Görtler失稳模态之于流向负曲率(凹面)区域[18-20]；附着线不稳定模态之于后掠翼抛物化前缘等[21-22]。对于一些特定复杂模型，转捩甚至可能是通过多种失稳模态相互作用完成的。

长期以来，转捩机理研究一般基于平板、槽道、圆锥等简单外形开展，虽然取得了大量的研究进展，但例如模态干扰/转换、攻角效应、钝度效应等的认知还存在不足甚至相互矛盾之处，对复杂飞行器的转捩预测与控制能力不足，飞行器相关设计(如热防护系统设计)时不得不采用较大的设计余量。目前，国内外已经开始重视转捩机理研究与真实飞行之间的匹配，飞行试验也越来越多地参与其中，比如美国近十多年来从HIFiRE-1的圆锥发展到HIFiRE-5的椭圆锥[23]，再发展到近两年的多曲面体边界层转捩(Boundary Layer Transition，BLT)[24]，所涉及的流动和转捩机理也越来越复杂。中国空气动力研究与发展中心(CARDC)成功完成了高超声速转捩研究的MF-1 飞行试验[25-27]，该试验主要研究圆锥边界层第二模态失稳导致的转捩问题。

纵观国内外，目前所用的高超声速转捩研究标模仍然存在不足。不论是HIFiRE-1和MF-1的圆锥外形，还是HIFiRE-5的椭圆锥，甚至是BLT的四象限曲面外形，都与真实高超声速飞行器有较大差异，且有的外形不是全解析光滑外形，比如HIFiRE-5外形的头部与锥身的过渡段不是解析的，需要采用数模定义，不利于研究人员相互交流。

为进一步研究三维复杂外形的高超声速飞行器边界层转捩问题，CARDC提出并设计了一款更接近真实飞行器典型气动布局特征、全数学解析光滑的升力体模型，名为高超声速转捩研究飞行器(Hypersonic Transition Research Vehicle，HyTRV)。本文针对HyTRV模型，主要利用高精度数值模拟方法分析基本流特性，利用线性稳定性理论(LST)和eN方法分析稳定性特性，为开展更多更细致的数值模拟、理论分析、风洞试验和飞行试验研究给出参考建议。

1 HyTRV外形与计算参数

1.1 HyTRV外形

HyTRV外形为全数学解析光滑的升力体外形，如图1所示。头部区域为长短轴比2:1的椭球型，下表面逐渐光滑过渡到长短轴比4∶1的椭圆型，上表面设计成由CST函数与椭圆函数共同控制的“几”字形状。为了表述方便，上表面的最高点称为模型的顶端，上表面两侧向内弯曲的地方称为腰部，下表面的最低点为椭圆型的短轴端，最低点连线称为下表面中心线。在上表面与下表面之间的连接区域对应于椭圆型的长轴端，其位置类似于后掠前缘，称为前缘附着线(简称附着线)。

图1 HyTRV外形

1.2 计算参数

本文选择风洞试验工况作为计算工况，以便后续风洞试验研究参考，参数见表1。其中，Ma∞代表来流马赫数，Re代表单位雷诺数，α′代表攻角，向上为正，p0代表总压，T0代表总温，T∞代表来流温度，Tw代表壁面温度。

表1 计算工况

2 数值计算与稳定性分析方法

2.1 数值模拟方法

针对HyTRV模型，本文以贴体曲线坐标系下的三维守恒型Navier-Stokes方程为流动控制方程。

由于边界层稳定性分析对基本流场的精细度要求较高，因此采用高精度数值格式。无黏项采用五阶精度的加权紧致非线性格式(WCNS)[28-29]；黏性项采用五阶精度的半节点/节点交错格式[30]，边界上采用三阶精度单侧差分格式；时间项采用隐式LU-SGS方法[31]，并采用SFD (Selective Frequency Damping)方法[32]提高计算收敛能力。壁面采用无滑移、等温条件；远场给定自由来流；出口为线性外推。

2.2 稳定性分析方法

根据线性稳定性理论，小幅值扰动可写成行进波形式：

(1)

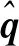
eN方法是基于LST的一种转捩预测方法，基本理念是边界层内各种频率和空间波数的扰动波进入不稳定区域后，其幅值将被放大，放大倍数可表示为eN；对于不同频率和空间波数的扰动波，其开始失稳的位置和增长率通常不相同；所有扰动波幅值放大倍数的N值曲线构成包络线，即为整个边界层扰动演化的幅值曲线。可通过包络线N值大小来判断转捩是否发生。对于二维转捩问题，扰动幅值沿流向ξ方向放大，其N值可表示为

(2)

式中：ξ0是扰动波刚进入中性区域的流向位置。对于一般三维问题，还需要考虑周向变化，因此式(2)还需要考虑周向波数及增长率以及沿三维空间方向的积分路径。然而周向波数沿空间方向一直变化，势必增加迭代求解难度。本文采用天津大学罗纪生团队发展的局部区域等效展向波数法[34]确定扰动波的周向波数和积分方向。三维问题的eN求解方法和软件开发思路具体见文献[35]。

2.3 网格无关性验证

为验证网格无关性，流场计算和稳定性分析测试了3套网格，半个模型(不计头部)流向×法向×周向的网格数分别grid1：1 310万(211×201×309)，grid2：2 354万(211×361×309)，grid3：4 901万(301×361×451)。图2在3套网格下比较了工况1(表1)的基本流，可见基本流等值线基本完全重合(图2(a))，速度剖面也基本完全重合(图2(b))，表明这3套网格的网格密度在计算基本流方面已经足够。图中：η表示垂直壁面方向上的坐标，L为升力体总长度。图3给出了3套网格下的N值对比结果，可见在大部分区域的N值等值线也基本完全重合，仅在中心线附近有所差别。造成这种差别的原因是该区域的基本流高度三维化，不稳定模态对基本流的变化更为敏感，稳定性分析对基本流要求更高。由此说明这3套网格在除流向涡区域外的其他区域中流向、法向和周向均满足网格无关性。本文选用grid2，即211×361×309的网格进行更详细的分析。

图2 不同网格下x/L=0.625处横截面流向速度云图与不同周向位置的流向速度剖面

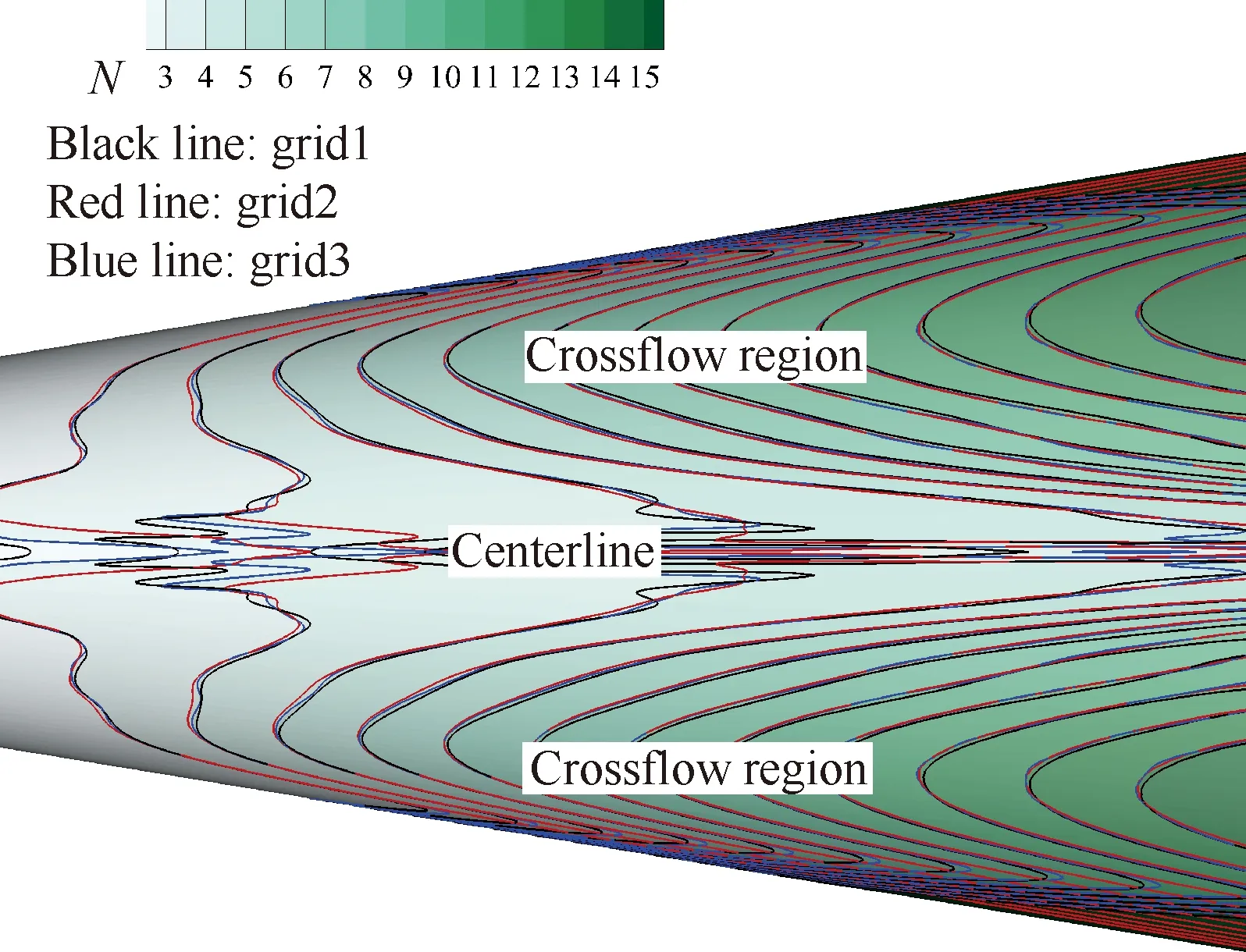
图3 不同网格对应的N值云图(下表面)

3 HyTRV流场

3.1 流向涡

针对表1中工况1～6，利用高精度数值模拟获得HyTRV基本流场。图4和图5分别给出不同攻角下的压力p云图和流向速度云图,4个截面位置为x/L=0.106 3,0.312 5,0.625 0,0.937 5。图中：HPZ指高压区，LPZ指低区。图6给出工况1近壁区的流线分布。由图4(a)可以看出，根据模型的外形特征，模型的附着线和顶端附近的激波强度比下表面中心线和腰部强，前两者激波后的压力比后两者高，因此横截面上存在周向压力梯度。为平衡周向压力梯度，流动从高压区(附着线和顶部)向低压区(下表面中心线附近和腰部)汇聚(图6)，汇集到一定程度后形成流向涡结构，如图5(a)所示。当攻角增加时，下表面中心线附近压力增大，导致下表面流向涡结构变扁；上表面顶端压力减小，低压区逐渐由腰部向顶端移动，导致腰部流向涡结构逐渐移向顶端(图5(b))。攻角为4°时，上表面靠近附着线的区域又出现一种低压区(图4(c))，对应多出一个流向涡结构(图5(c))。攻角为6°时，上表面顶端区域成为低压区(图4(d))，对应形成流向涡结构(图5(d))。继续增加攻角，下表面中心线附近压力继续增大，以致下表面的周向压力梯度逐渐消失(图4(f))，因而流向涡结构继续扁平而最终消失(图5(f))；上表面两个低压区进一步扩大和增强，导致上表面中心线附近出现流向涡，腰部的流向涡也逐渐向上表面中心线靠近，多个流向涡相互干扰，涡结构变得更加复杂(图5(e)和图5(f))。

图4 不同攻角下的压力云图

图5 不同攻角下的流向速度云图

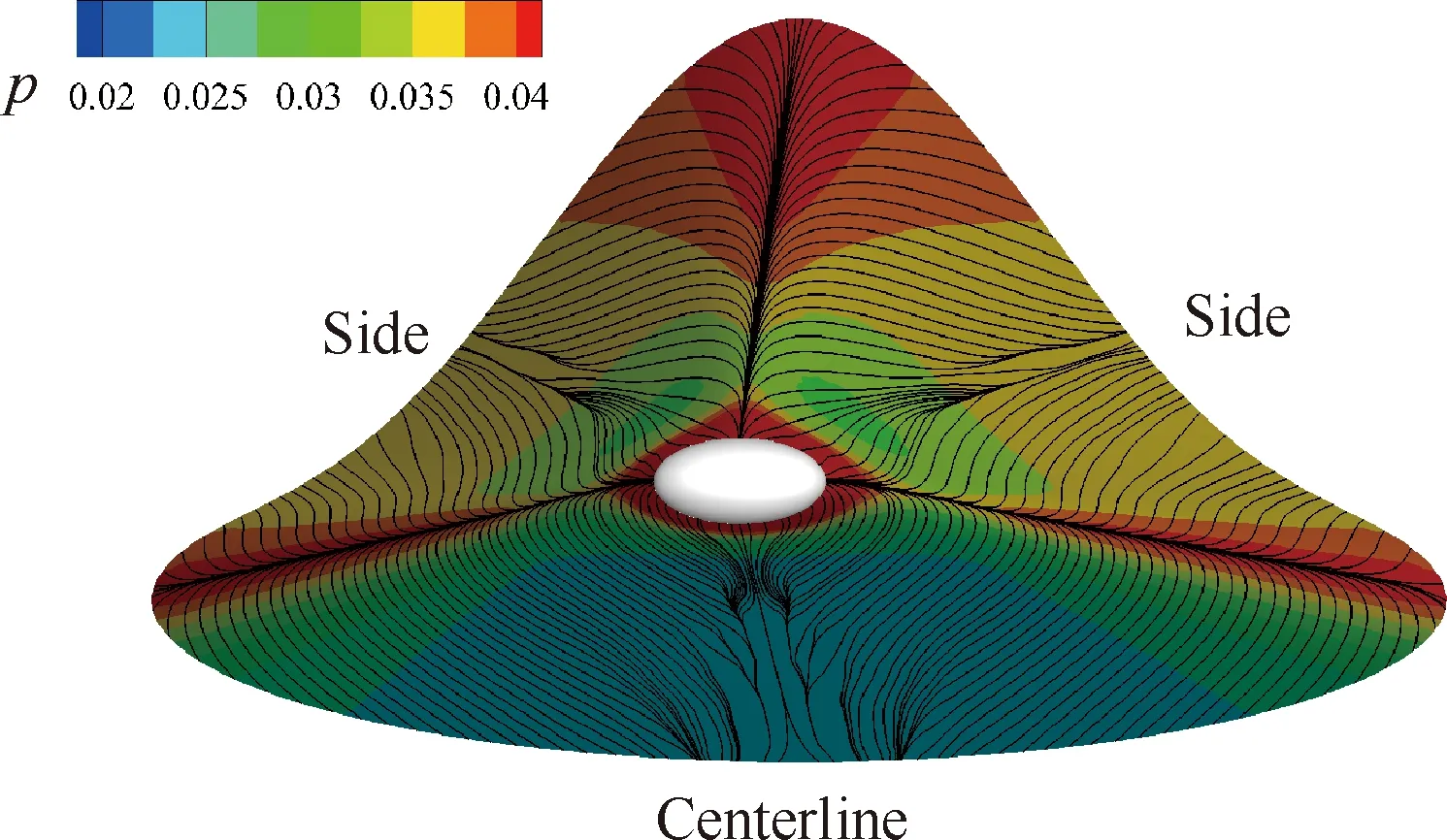
图6 0°攻角流场在中心线附近和腰部区域流线汇聚(工况1)

基于流向涡随攻角的变化情况，建议从如下3个方面研究HyTRV模型的流向涡失稳：

1) 针对小攻角工况研究下表面中心线的流向涡失稳及转捩机理。此流向涡的形成机制与HIFiRE-5椭圆锥模型短轴处流向涡形成机制相同，流向涡都呈现蘑菇状分布。

2) 针对大攻角工况研究上表面多个流向涡干扰及转捩机理，可用来表征真实高超声速飞行器大攻角飞行时的背风面转捩情况。

3) 针对攻角变化情况研究不同扁平程度的流向涡失稳及转捩机理。

流向涡产生之前，通常要经历横流阶段，横流失稳与流向涡失稳相互干扰，可能会出现更多的涡/波结构。下文将对HyTRV的横流特征进行分析。

3.2 横流

在流线汇聚之前，边界层内存在由高压区到低压区的横向流动，其速度从壁面到边界层外缘为从零迅速增加然后迅速减小直至边界层外缘附近时再缓慢减小接近于零，该横向流动称为横流。边界层外的流动受周向压力梯度影响很小，基本沿无黏势流向方向，因此在横流区域中边界层外的势流流线与边界层内黏性流线之间存在较大的夹角。图7给出了表1工况1的模型下表面和侧面的势流流线与壁面黏性流线的分布。根据这种特性，图中可以判断出在0°攻角下横流主要分布在附着线与中心线之间、腰部与附着线之间、顶端与腰部之间的3个区域，分别记为Zone 2、Zone 3、Zone 6。

图7 0°攻角的势流流线和近壁面流线分布(工况1)

横流雷诺数Recf常用来判断流场中横流区域分布及其强度。横流雷诺数越大，说明横流效应越强。计算形式为

(3)

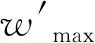
图8和图9分别给出不同攻角上下表面的横流雷诺数云图。可以看出，除去腰部和下表面中心线附近的流向涡区域，当攻角为0°时，有3个区域的横流雷诺数较大，分别对应Zone 2、Zone 3和Zone 6。说明这3个区域的横流效应比较强，且下表面Zone 2更强。随着攻角的增加，下表面Zone 2的横流雷诺数逐渐减小，上表面Zone 6也减小，但Zone 3却逐渐增大。这是因为攻角增加时下表面周向压力梯度逐渐减小，横流效应逐渐减弱；而上表面低压区从腰部逐渐移到顶端，使Zone 6区域变窄，Zone 3区域变宽，同时顶端压力逐渐减小，使Zone 6压力梯度逐渐减小，从而Zone 6横流效应减弱，而Zone 3横流效应增强。

基于横流强度随攻角的变化情况，建议从如下3个方面研究HyTRV模型的横流失稳：

1) 针对0°攻角工况研究3个相对独立区域的横流失稳及转捩机理。这3个相对独立的横流区域为下表面的Zone 2和上表面的Zone 3和Zone 6，且以Zone 2的横流最强，分布区域最大。

2) 针对不同攻角工况研究不同横流强度的失稳及转捩机理。此时下表面的Zone 2区域是比较理想的研究区域，横流强度随着攻角增加而逐渐减弱(图8)。

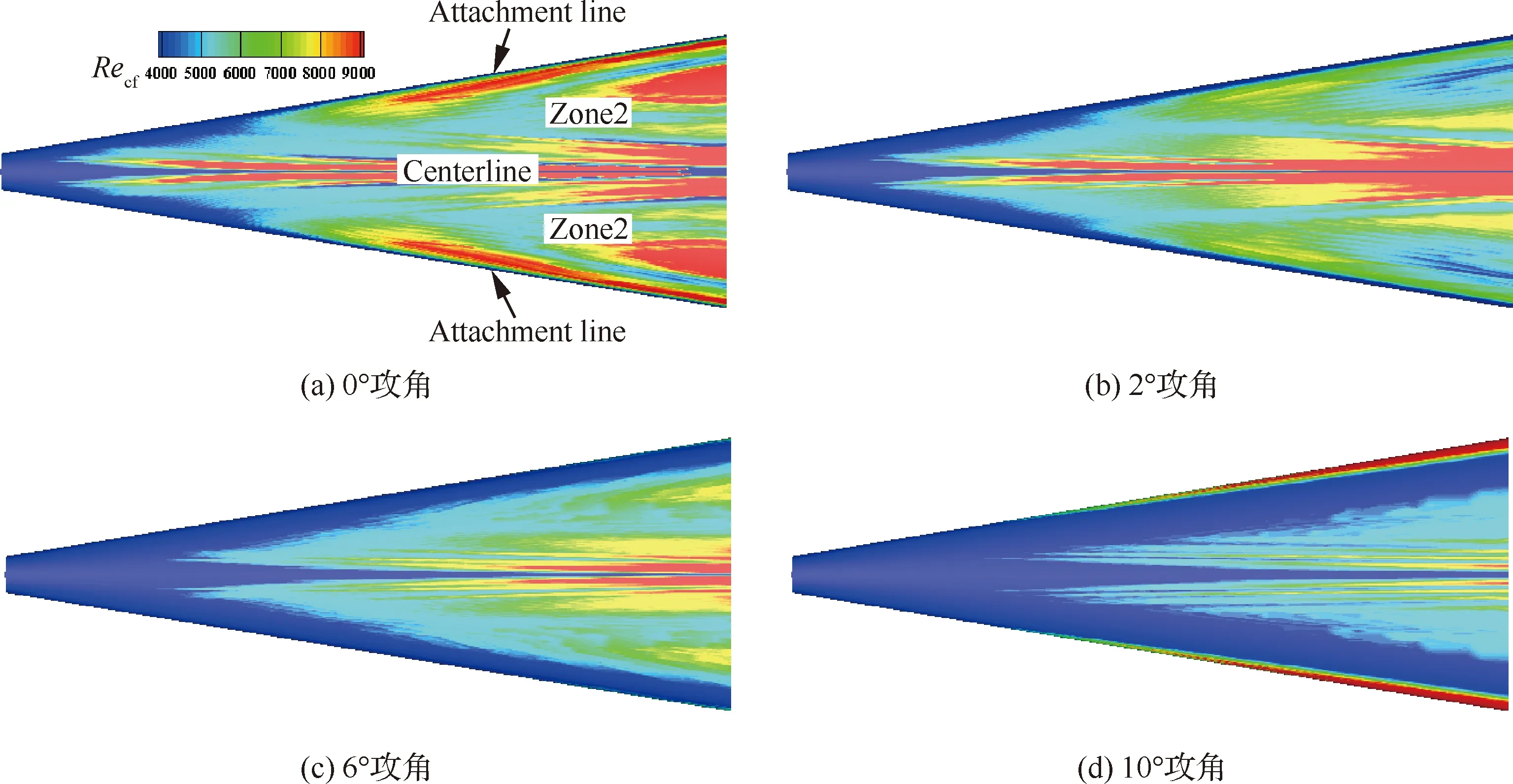
图8 不同攻角下表面的横流雷诺数分布

3) 针对中等和大攻角(比如6°～10°攻角)研究上表面Zone 3区域的横流失稳及转捩机理(图9)。此时Zone 3区域类似于高超声速飞行器“机翼”背风面的横流区域。

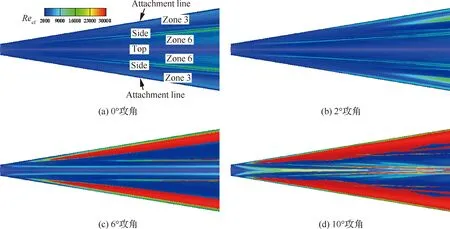
图9 不同攻角上表面的横流雷诺数分布

4) 针对HyTRV模型腰部区域，应对横流失稳与流向涡失稳的相互干扰做详细研究。因为横流区域与流向涡区域交替出现，横流不稳定性的参与，会引入更多的涡/波结构。

4 稳定性与eN分析

对第3节提到的流场区域，除了LST失效的流向涡区域外，其他区域都可采用LST进行稳定性分析，从而求解出该区域的不稳定模态N值分布。下表面中心线附近和腰部(或者更多部位)的流向涡结构是一个法向和周向变化的二维结构，LST分析失效，但可采用二维全局稳定性(BiGlobal)或求解三维抛物化稳定性方程(PSE3D)的分析方法，本文暂不研究。

分析表明所有的第一模态都是稳定的，这可能是由于马赫数较高、壁温较低，故不展示第一模态的分析结果。附着线位置的流场特征类似于圆锥表面的母线，其附着线不稳定性也是边界层的一种失稳机制，稳定性分析需要考虑。下文主要从横流失稳模态、第二模态、前缘附着线失稳模态讨论HyTRV的边界层稳定性特征。

4.1 横流失稳模态

图10和图11给出表1工况1的横流模态不同频率下的N值分布，频率范围为0～40 kHz，图中分别给出上下表面的结果。可以看出在第3节提到的3个区域中均存在对应的横流不稳定模态，如图10(a)和图11(a)所示，其中下表面Zone 2中的模态最不稳定。增加模态频率对比分析发现，Zone 6中0 kHz频率的定常横流模态相比其他频率最不稳定。但并不是所有横流模态都是这样的，Zone 2和Zone 3中最不稳定频率大概在20 kHz(见图10(b)和图11(c))，N值最高可达15。需要注意的是，图10(b)和图11(c)的下表面中心线附近和图10(b)和图11(c)中的腰部附近的狭长不稳定区域位于流向涡范围，失稳特征需要专门研究，此处不讨论。

图10 工况1下表面横流模态不同频率下的N值分布

图11 工况1上表面横流模态不同频率下的N值分布

图12和图13分别给出表1工况1、2、4、6、7上下表面的横流模态N值分布，N值包络的频率范围是0～30 kHz。可以看出，在0°攻角时，最不稳定的横流模态分布在下表面Zone 2。随着攻角增加，下表面Zone 2横流模态N值减小，上表面N值增加。当攻角为2°时，上表面N值已经超过下表面。同时注意到，当攻角增加时，Zone 6中的横流模态逐渐消失，而Zone 3中横流模态区域不断扩大，N值不断增加。直到攻角为10°时，由于上表面存在复杂多变的流向涡结构，求解出的横流模态N值覆盖在整个上表面区域。图12(e)和图13(e)显示，增加单位雷诺数，Zone 2、Zone 3和Zone 6这3个横流区域的N值均显著增加。

图12 工况1、2、4、6、7下表面横流模态的N值分布

图13 工况1、2、4、6、7上表面横流模态的N值分布

建议风洞试验或飞行试验时参考不同攻角不同区域的横流失稳特征进行传感器选型与测点布置。

4.2 第二模态

图14和图15分别给出表1工况1、2、4、6、7上下表面的第二模态N值分布，N值包络的频率范围是100～3 000 kHz。可以看出，在前面提到的3个区域中不仅存在横流不稳定模态，也存在第二模态。而且随着攻角增加，Zone 2和Zone 6中第二模态逐渐消失，Zone 3中先是增大，约2°攻角时N值开始减小。对比横流不稳定模态，第二模态的N值略小，因此这3个区域很可能是以横流模态为主导转捩。图14(e)和图15(e)显示，增加单位雷诺数(对比图14(a)和图15(a))，这3个区域第二模态的N值也显著增加，但仍小于横流模态。另外可以观察到，在附着线附近，N值非常大，远大于横流模态，具体分析见4.3节。

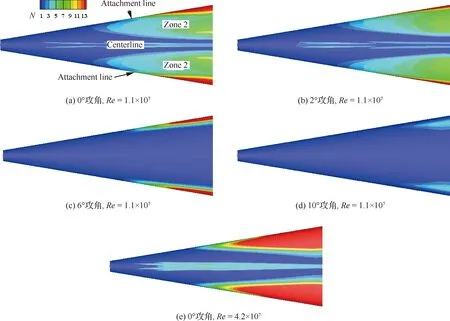
图14 工况1、2、4、6、7下表面第二模态的N值分布

图15 工况1、2、4、6、7上表面第二模态的N值分布

由于大部分横流区域也存在第二模态，且在某些工况(比如0°和2°攻角)条件下N值接近横流失稳模态的N值，所以建议加大第二模态与横流模态的干扰/竞争、甚至非线性相互作用等方面的研究。第二模态扰动波的频率基本在100 kHz以上，频率较高，试验测量时需要留意。

4.3 附着线失稳模态

图16 附着线对应的中性曲线

图17 800 kHz附着线不稳定模态对应的增长率和相速度

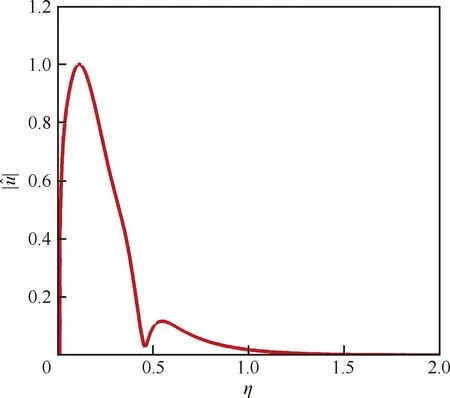
图18 800 kHz附着线不稳定模态的流向速度特征函数

在附着线处，每个频率从中性曲线下支界开始对增长率进行积分得到N值包络线，如图19所示。图19(a)显示，N值在x/L=0.94处达到20.3，对应频率约为755 kHz。改变攻角和单位雷诺数时，x/L=0.94处的N值及频率均发生变化，如图19所示，结果见表2。可以看出，当攻角为2°时，N值和频率均微弱增加；继续增加攻角，N值和频率均逐渐减小，而且临界位置逐渐靠近下游。另外，增加单位雷诺数，N值和对应频率均明显增加(见图19(g))。

表2 x/L=0.94处N值及对应频率

建议后续通过风洞试验进一步验证附着线失稳模态的物理本质，同时需要特别留意附着线失稳扰动波的频率非常高，在有的工况下甚至超过1 000 kHz (图19(g))，这已经超过大部分传感器的响应频率，比如国内外采用的高频PCB压力传感器的响应频率也仅为1 000 kHz的量级。

图19 工况1～7第二模态的N值分布

4.4 eN分析与试验对比

针对HyTRV模型，CARDC在∅2 m激波风洞中进行了初步的风洞试验验证，本文仅取表1工况1，模型是上述的1/2缩比模型。风洞试验中采用温敏漆获取转捩阵面，然后与eN分析结果进行对比分析。在eN分析中，N值包络的频率范围选为0～3 000 kHz，囊括了横流模态、第一模态(虽然是稳定的)、第二模态以及附着线不稳定模态。N值显示的是当地最不稳定的模态。如前面所述，Zone 2、Zone 3和Zone 6以横流不稳定模态为主，附着线附近区域可能是以第二模态为主。针对模型的下表面，图20给出eN分析与风洞试验的对比结果，下游深红色区域表示试验模型表面的温度较高，为湍流区，黑色曲线表示eN分析得到的N值等值线，Lt为风洞模型长度。可以看出，风洞试验中Zone 2区域发生了转捩，转捩位置从x/Lt≈0.75的地方开始，对应N值约为5.6，对应频率在10～40 kHz之间，说明Zone 2发生转捩是由非定常横流失稳模态引起的。另外，附着线附近的表面温度较高，其原因既可能是边界层转捩引起的，也可能是附着线前缘的脱体激波引起的。但是因为风洞试验测量窗口限制及流场视角问题，本次试验还无法判断附着线转捩位置。中心线附近约在x/Lt≈0.56位置温升梯度开始增大，可能是流向涡失稳引起的转捩，需要进一步分析。