一种自动化并行重叠网格隐式装配方法
2021-07-07郭永恒江雄肖中云王子维卢风顺
郭永恒,江雄,肖中云,王子维,卢风顺
中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000
随着大规模并行计算技术的不断进步,计算流体力学(CFD)能够处理的非定常数值模拟问题更加丰富[1];对多体相对运动的情形,比如共轴双旋翼直升机的气动干扰[2-3]、超声速子母弹的播撒[4]、运载火箭低空大动压头罩分离[5]、水陆两栖飞机静水滑行[6]、外挂式导弹的发射[7]等,单纯的结构或非结构网格已不能满足分析需求。凭借较高的灵活性,重叠网格装配已发展成为处理上述问题的关键技术之一。
重叠网格装配有显式与隐式两类方法。在网格生成阶段,显式方法[8]需要在固壁附近构造出挖洞边界以辅助划分单元类型,同时还要人工指定多组部件网格的重叠关系矩阵,从而导致装配自动化水平偏低,难以适应网格运动时的分析需求。相比之下,隐式方法摒弃了人工洞边界,结合网格拓扑结构以及网格组之间的度量关系进行几何计算,能够极大地提升重叠装配的自动化水平。然而,在隐式装配方法并行化过程中,当网格规模和重叠区域增大时,算法涉及的查询运算量和进程间的通信压力急剧攀升,成为制约隐式装配技术工程应用的瓶颈问题[9]。
为了提高重叠网格隐式装配效率、拓展其工程应用范围,大量专业化的重叠分析软件得以发展起来。Overflow[10]与Beggar[11]是基于重叠网格的流场模拟软件,已在工程实践中得到广泛应用,但其重叠分析模块与流场求解器紧密耦合,难以被第三方求解器使用。PEGASUS[12]能够并行装配运动部件网格,但其分析结果只能通过计算机文件系统进行传输,且大量参数的人工控制导致其自动化水平较低。SUGGAR装配软件与插值工具库DiRTlib结合[13]能够很好地解决结构/非结构重叠网格的装配问题,并且可以嵌入到多种流场解算器中;但进行复杂构型网格挖洞时,控制参数需要经大量尝试才能达到合适的水平。SUGGAR++[14]在自动化程度、鲁棒性以及效率方面有了较大改进,但是其直接挖洞算法无法适应几何构型不封闭的情况。重叠网格装配中间件TIOGA[15]将快速搜索算法和动态负载平衡技术相结合,大幅提升了重叠网格的并行装配效率;但算法的内在属性导致隐式挖洞边界光滑性欠佳,进而影响流动模拟品质的提升。
综合来看,常见的重叠网格隐式装配方法皆起源于Lee和Baeder提出的壁面距离准则[16-17]。在其并行化实现过程中,当前部件网格节点到自身所属壁面距离的计算、当前部件网格节点到其他部件壁面距离的插值以及贡献单元的存在性判断共同构成了隐式装配的自动挖洞过程。正是上述3个步骤的高度耦合使几何分析过程呈现出复杂和低效性质,初始阶段节点无差别查找操作影响并行装配效率。
针对上述问题,本文根据壁面距离准则,构造出一种高度自动化的重叠网格隐式装配方法,其基本思路是:首先,结合协方差分析、切割盒子等快速算法,将壁面距离计算与贡献单元存在性判断解耦,实现网格组动态重叠关系的自动化识别;其次,结合集合分析,设计出并行化的自动挖洞算法;最后,通过快速查询方法建立重叠单元与贡献单元的插值关系。其中,第1节使用集合论语言对重叠网格隐式装配算法进行描述;第2节详细介绍算法的并行实现细节,包括提升效率和自动化水平的各种关键技术;第3节使用多部件重叠的网格模型测试算法的并行效率,并结合流场解算器测试重叠插值结果的准确性;最后给出结论与展望。
1 重叠网格隐式装配算法的集合论表示
现有的重叠网格隐式装配方法都是依据“网格节点到固体壁面的距离”进行构造的[18],但是在实现过程中,流场计算单元、重叠插值单元以及洞内单元的划分准则具有很大的差异;例如,很多研究者[18-20]根据网格图形范例进行算法描述。对于复杂几何构型、多部件网格重叠、部件网格外缘边界与挖洞边界相交等复杂情形,图示法的严谨性便显得不够充分。因此,需要使用集合论语言对重叠网格隐式装配原理进行严格地描述。
设整个求解域上包含M个部件的集合为CompSet,对于任意部件compi∈CompSet都存在网格组gpi与之构成一一对应关系,其中i∈{1,2,…,M}。设网格组gpi的节点集合、面单元集合、体单元集合依次为NodeSeti、FaceElemSeti及VolElemSeti,那么根据计算流体力学通用符号系统(CFD General Notation System, CGNS)定义的拓扑结构,三者之间建立起空间链接关系;设固壁边界面上的网格节点集合为SolidNodeSeti,它与NodeSeti的关系为
SolidNodeSeti⊂NodeSeti
(1)
1.1 网格组节点集合划分
任取一个网格节点P∈NodeSeti,设它到第j个部件壁面的距离为
d(P,SolidNodeSetj):=
MinVal{d(P,Q)|Q∈SolidNodeSetj}
(2)
特别地,当i=j时,d(P,SolidNodeSetj)是节点到自身网格组壁面的距离。如果存在一个网格组gpj(j≠i)同时满足如下条件:
(3)
每个网格组节点集合NodeSeti都被划分成活跃节点集合PosNodeSeti与非活跃节点集合NegNodeSeti,即
NodeSeti=PosNodeSeti∪NegNodeSeti
(4)
当网格节点集合完成式(4)的分类后,便得到重叠网格的挖洞边界。通过拓展挖洞边界处的体单元,即可实现洞内单元、重叠单元以及场单元的自动识别。
1.2 网格组单元划分
每个网格组gpi的单元划分包括4个步骤(在不引起歧义的情况下,文中的集合符号均省略下标i):
1) 在部件网格组gp上,由于与延拓型物理边界面相邻的体单元不可能在计算过程中扮演场单元的角色,进而也不可能成为其他网格组上重叠单元对应的贡献单元,因此VolElemSet可划分为一般单元集合GeneralElemSet与延拓型单元集合ExtendElemSet,即
VolElemSet=GeneralElemSet∪ExtendElemSet
(5)
2) 如果体单元velem∈VolElemSet的所有节点皆为非活跃点集合NegNodeSet中的元素,那么定义velem为非活跃单元。如果体单元
velem∈GeneralElemSet=VolElemSet∩
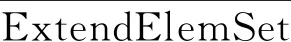
(6)
的所有节点皆为活跃点集合PosNodeSet中的元素,那么定义velem为活跃单元,否则定义为过渡单元。不妨记活跃单元、非活跃单元以及过渡单元的集合分别为PosElemSet、NegElemSet和NeuElemSet,将

(7)
定义为延拓型重叠单元的集合。易知
VolElemSet=PosElemSet∪NegElemSet∪
NeuElemSet∪ExtendOvsSet
(8)
其中:等号右侧4个元素之间互不相交。
式(7)表明,经过壁面距离准则筛查后,如果延拓型单元不属于非活跃单元集合,那么它将被识别为重叠单元。
3) 任取体单元neg∈NegElemSet,如果存在体单元neu∈NeuElemSet,使
NodeList(neg)∩NodeList(neu)≠∅
(9)
那么将neg归入一般性重叠单元集合GeneralOvsSet,否则将其归入洞内单元集合HoleElemSet。NodeList(neg)和NodeList(neu)分别表示体单元neg和neu的节点元素集合。此处单元分类的几何意义是:在洞边界附近,与过渡单元相邻的非活跃单元转化为重叠单元;与过渡单元不相邻的非活跃单元转化为洞内单元。
4) 场单元集合的定义为
FieldElemSet:=PosElemSet∪NeuElemSet
(10)
需要说明的是,过渡单元是同时具有活跃节点和非活跃节点的体单元,因为它恰好跨越重叠挖洞边界,所以将与另一网格组上的过渡单元交织在一起;为避免不同网格组上的重叠单元互为对方的贡献单元,在式(10)中,过渡单元最终转化为场单元。重叠单元集合定义为
OvsElemSet:=GeneralOvsSet∪ExtendOvsSet
(11)
至此,结合第3)步的洞内单元HoleElemSet,最终完成了单元分类
VolElemSet=FieldElemSet∪HoleElemSet∪
OvsElemSet
(12)
从本文重叠网格装配算法的构造过程可以看出,与图示法相比,基于集合论语言的描述方式具有如下4个方面的优势:
1) 具有普适性,不受网格几何形状复杂程度或面、体单元类型多样性的影响。
2) 能够清晰表述多组网格重叠时的复杂映射关系。
3) 能够精确判断延拓型外缘边界与距离挖洞边界相交等复杂情形。
4) 可作为算法分析的有力工具,辅助提升并行装配效率。
2 自动化并行重叠网格隐式装配方法
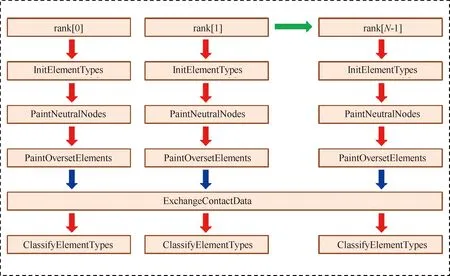
图1显示重叠网格的并行装配流程,包含几何信息输入、网格组自动配对、重叠单元隐式装配、插值信息输出等4个步骤。

图1 重叠网格并行化装配流程
步骤1左侧(蓝色)部分是算法主线,依次为分区网格几何信息的输入、部件网格组之间重叠关系的自动识别、重叠单元的隐式装配以及插值信息的输出。
步骤2右上(绿色)部分是几何数据的基本构成,包含边界映射信息、部件网格进程分组信息、分区网格几何数据以及网格块对接信息。其中,边界映射信息主要用来识别固体边界面以及部件网格的外延拓边界面;在挖洞过程完成后,网格块对接关系用来跨进程识别重叠单元。
步骤3右中(黄色)部分是重叠装配所需的主要数据结构,它们根据原始几何信息构建。其中,部件网格极小内部盒子、外部盒子用来辅助网格组自动配对;覆盖固壁节点的递归盒子用来对查询节点进行初步筛查;空间体单元的二叉树结构用于单元节点或格心贡献单元的快速查询。
步骤4右下(橙色)部分显示具体的重叠单元隐式装配过程,包括并行计算节点到自身部件和邻居部件距离、初筛待查询节点、确认节点激活属性、识别挖洞边界、识别重叠单元以及查找贡献单元等7个步骤,(绿色)虚线条展示了各步骤所需的数据结构。
2.1 重叠网格组并行分区策略
重叠网格并行装配算法是与网格组分区策略紧密结合在一起的。假设存在N个进程参与流场计算,那么上述M个网格组存在两种分区策略。
策略T1把全体网格组包含的网格块视为一个整体,根据体单元数负载均衡原则,使用Greedy算法或METIS算法进行统一分配,如图2(a)所示。
策略T2结合网格组体单元数在整体网格中所占的比重,计算其所需的进程数,然后将当前网格组均匀分配到相应的进程组中,如图2(b)所示。

图2 两种剖分策略对比
文献[21]中的重叠网格装配方法使用T1策略能够保证体单元分配结果的高度均衡性,但也容易使每个网格组上形成过多的碎片化网格块,从而影响并行计算效率。在重叠网格并行化装配算法中,两个网格组涉及的进程组间需要频繁进行数据通信;此时使用较少的进程数容纳当前网格组的各个网格块,能够有效提高算法的并行效率。因此,采用T2策略进行网格分区。
2.2 网格组自动配对技术
在传统的重叠网格装配算法中,需要在图形界面下人工指定网格组间的重叠关系,比如使用逻辑矩阵来描述。对于多体相对运动的情形,各网格组之间的相对位置与重叠关系通常是动态变化的,这些特点决定了人工配对操作难以满足重叠网格自动化装配的需求。常兴华等[22]为提升大规模重叠网格的装配效率与自动化水平,使用包含每个网格块的长方体辅助判断重叠关系,其中长方体表面分别与坐标轴垂直。这种方法本质上是使用大量的简单长方体实现网格组区域的几何逼近,将网格组重叠关系判断问题转化为相应长方体集合的求交逻辑运算;但是,这种方法导致过于碎片化的分区结果,根据Navier-Stokes (N-S) 方程的数值迭代理论,它将使收敛历程大大延长,从而降低流场求解的效率。受文献[15]中方向适应型边界盒子的启发,本文建立了关于部件表面网格点坐标的协方差矩阵,结合谱分析技术,构造了部件网格组的极小内部盒子与极小外部盒子,以此辅助网格组区域重叠关系的快速识别。
在第i个部件compi∈CompSet上,设固壁节点集合SolidNodeSeti的元素个数为ms,那么可以把所有节点的坐标依次存储于3个ms维向量中:
(13)
式中:(xms,yms,zms)为编号s的固壁节点空间坐标。协方差矩阵为

(14)
根据协方差运算的可交换性可知:D为对称矩阵,其特征系统中3个特征向量两两正交。通过Householder变换可将其约化成三对角阵,进一步使用QR方法即可得到D的全部特征值及其特征向量。设特征向量的规范化结果为
ns=[As,Bs,Cs]Ts=0,1,2
(15)
给定方向序号s,以ns为基准法向量建立空间平面参数方程:
Asx+Bsy+Csz+λs=0
(16)
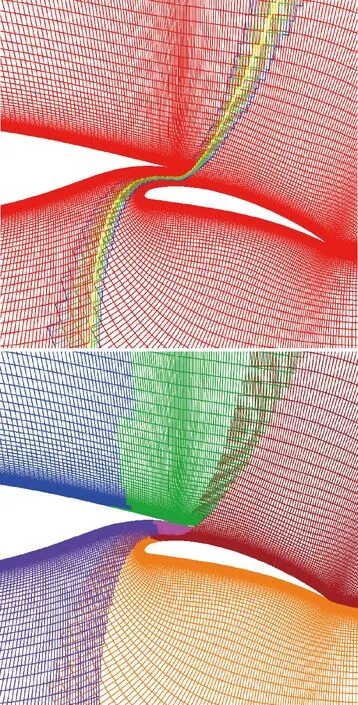
依次遍历SolidNodeSeti中的元素并取参数λs的上下确界,即得方向部件的2个临界方程。3个特征方向的临界方程使部件表面网格包含在一个极小长方体内,称其为极小内部盒子MIBi,如图3红色线条所示。
如果保持特征方向不变,将上述运算中的集合SolidNodeSeti替换成整体网格组节点集合NodeSeti,那么整体网格组将包含在新的极小长方体内,称其为极小外部盒子MEBi,如图3蓝色线条所示。对网格生成有如下附加要求:极小内部盒子覆盖的空间区域包含在整个网格组区域中,这在网格生成过程中是容易实现的;同时,网格组外缘表面适当远离边界层网格也是提升重叠插值精度的要求。图3展示的是螺旋桨单叶片网格上极小内部盒子与极小外部盒子的包含关系,而图4展示了整个螺旋桨各部件网格相互重叠关系。
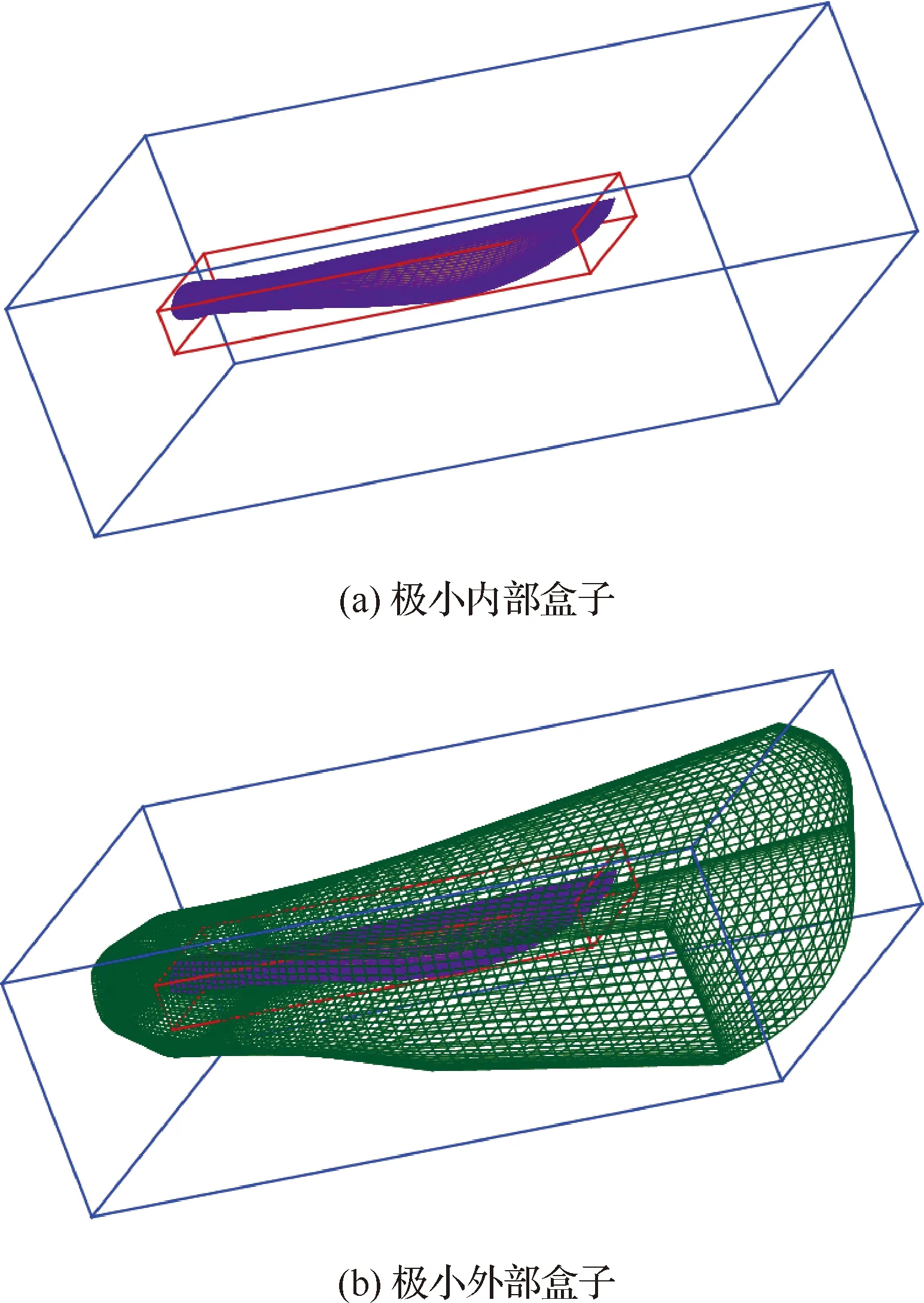
图3 螺旋桨单叶片极小内部/外部盒子

图4 螺旋桨叶片各部件网格重叠关系
任意给定网格组gpi,设其覆盖区域为Di,那么存在集合关系式
MIBi⊂Di⊂MEBi
(17)
对于当前网格组gpi(称为源网格组SG),如果对另一组网格gpj,关系式:
MEBi∩MEBj=∅
(18)
成立,那么
Di∩Dj=∅
(19)
即当前状态下gpi与gpj不存在相互重叠关系;否则,称gpj为与gpi存在可能重叠关系的目标网格组TG。式(18)的逻辑判断可以根据图5所示的分离平面法快速完成:依次遍历源网格组SG和目标网格组TG的3个特征方向,那么该式成立的充要条件为:存在以特征方向为法向量的空间平面SP,使MEBi与MEBj分居其两侧。图6描述了源网格组与目标网格组(为目标网格组的全局编号)之间的重叠关系,其中,与当前源网格组SG发生重叠关系的目标网格组TG的总数为L;在并行计算环境下,源网格组的各个子块grid_s分布在编号连续的NG个进程中,而它的某个目标网格组(以TG[2]为例)的各个子块grid_t分布在编号连续的MG个进程中。

图5 空间分离平面法
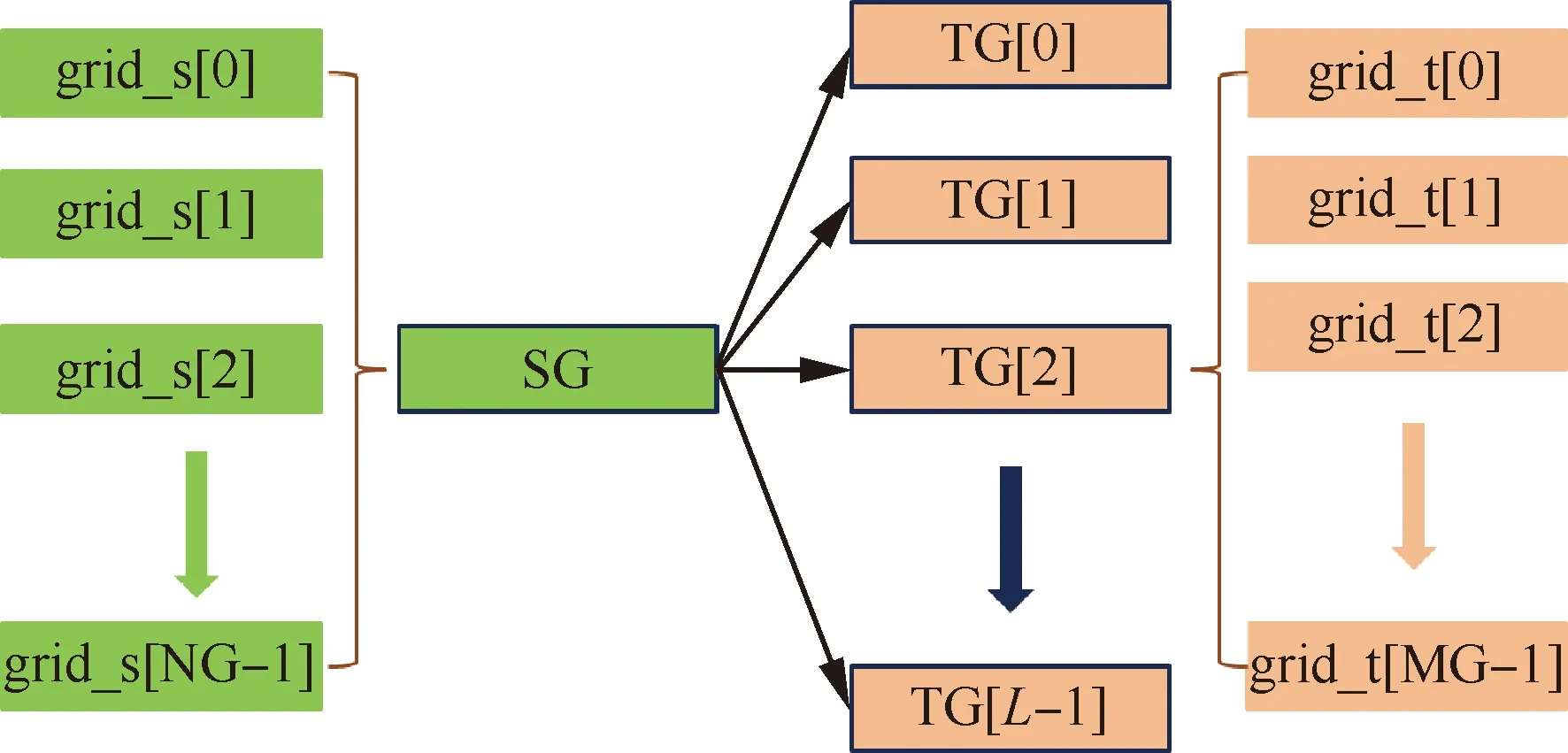
图6 源网格组与目标网格组的重叠关系
使用图6所示的映射关系,可以对多组网格间的复杂重叠关系进行分解。从整体上来说,优先遍历当前的源网格组SG;对于特定SG,局部遍历与之重叠的多个目标网格组TG。
2.3 自动挖洞的并行化实现
在第1节中,描述重叠网格自动挖洞的壁面距离准则包含两个方面内容:一是网格节点壁面距离的计算;二是网格节点与体单元之间的覆盖关系。在当前网格组gpi上,如果直接遍历集合NodeSeti并对每个网格点元素P∈NodeSeti同时执行上述分析,那么不仅会使程序编写难度急剧提高,而且会使源网格组与目标网格组之间的通讯压力迅速增长,进而限制该算法在大规模并行计算中的应用。反之,如果首先对NodeSeti中所有元素基于距离参数比较法计算距离参数,就可以大大降低判断节点与体单元覆盖关系时的计算量与通讯压力,其原理描述如下。
对于∀gpi所对应的目标网格组gpj(j=j0,j1,…,jL-1),如果∀P∈NodeSeti,条件C1:
d(P,SolidNodeSetj)>d(P,SolidNodeSeti)
(20)
成立,那么P∈PosNodeSeti。作为式(3)的互斥条件之一,式(20)使用单纯的距离判据排除了大量待查询的节点。
此外,结合2.2节关于极小外部盒子的定义可知,如果∀P∈NodeSeti,条件C2:
(21)
成立,那么可以推出
(22)
作为式(3)的另一个互斥条件,式(22)根据网格组的极小外部盒子的空间相对位置进行间接筛查,同样可知P∈PosNodeSeti。C1与C2称为距离初筛条件与覆盖初筛条件,据此可提升重叠网格并行化挖洞算法的效率。
图7描述了当前源网格组SG壁面几何信息的收集以及与各目标网格组TG共享的过程:非阻塞通讯模式下,在SG包含的各个进程组内,对相应网格块grid_si(i=0,1,…,NG-1,NG为分区后SG包含的网格块总数)上的壁面节点坐标序列进行数据压码操作,形成NG个二进制数据流solid_s,在主进程中通过数据容器solid_node_collector加以汇总后,分别在SG与TGj(j=0,1,…,L-1,L为SG对应的目标网格组个数)所在的进程组内共享并解码,形成完整的SolidNodeSet信息后,对节点壁面距离信息进行更新。
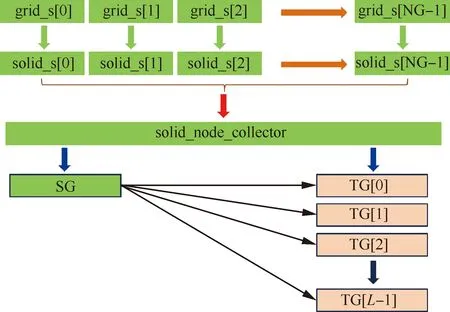
图7 源网格组壁面几何信息收集与共享
图8描述了节点壁面距离参数的定义:对源网格组SG(gpi)上任意给定网格节点P∈NodeSeti,令ds(P)∶=d(P,SolidNodeSeti)为P到SG壁面的距离,dtj∶=d(P,SolidNodeSetj)为P到TGj壁面的距离,其中j取0~L-1范围内的整数;令dt(P)∶=MinVal{dt[0],dt[1],…,dt[L-1]},那么,ds与dt就构成了距离比较判据的两个重要参数。在并行计算框架下,若直接对ds与dt进行计算,则存在两种方式:① 把P的信息发送L次,分别与SolidNodeSetj计算出dtj,然后通过全局规约操作得到dt值;② 把SolidNodeSetj的信息发送到P所在的进程,对其依次遍历,按最小值准则不断更新dt值。可见,方式①的通讯压力较大,全局规约操作将影响计算效率的提升,因此采用后一种方式计算ds与dt。
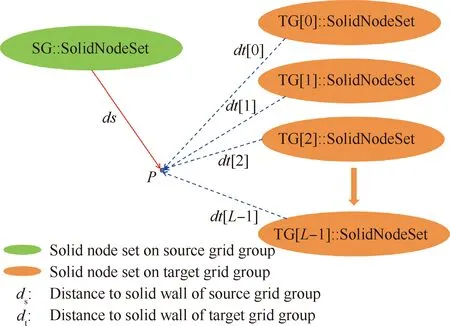
图8 节点壁面距离参数定义
空间节点的壁面距离是重叠网格隐式装配方法的关键参数之一,如果采用线性查找方法,遍历所有的壁面点后取最小值,那么,当壁面节点总数很大时,计算成本将急剧升高;同时,这种简单查找法也难以适应网格运动、网格自适应时壁面距离频繁更新的情形。相比之下,基于点集树形排序思想的方盒切割算法[23]能够很好地处理这一问题,它包括固壁点集临界长方体(方盒)序列的生成和最近距离点的查找两部分内容,其中,针对临界长方体序列的辅助分析,可以在点集遍历过程中动态排除无关的子集,从而大幅提升壁面距离的计算效率。
临界长方体序列的构造分为如下4个步骤:
步骤1取网格组gpi共享的壁面节点集合SolidNodeSet[i],沿着平行于坐标平面的方向,根据式(23)分析壁面节点坐标分量的上下界,构成临界长方体序列根结点的6个基本参数,它们分别是
(23)
步骤2在节点集坐标分量最大的变化区间上进行排序与二分法操作,构造当前节点集的左右子集以及相应的临界长方体参数。分别计算
(24)
不妨假设
δz<δy<δx
(25)
然后,对壁面节点序列按照x坐标大小排序,并采用二分法生成SolidNodeSeti的2个子集SubNodeSeti0与SubNodeSeti1。
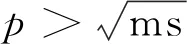
步骤4当临界长方体构造完成后,仅收集所有的叶子结点(不可分的临界长方体),形成壁面距离计算的基础查询数据集。经过若干层级的分解,原始的SolidNodeSeti可以写成一系列节点子集的并集,即
SolidNodeSeti=SubNodeSeti0∪SubNodeSeti1∪
…∪SubNodeSeti(NSub-1)

此时,对于每个SubNodeSetis,分别以空间平面
(26)
构成临界长方体Capsules,以此覆盖集合SubNodeSetis,如图9和图10所示。
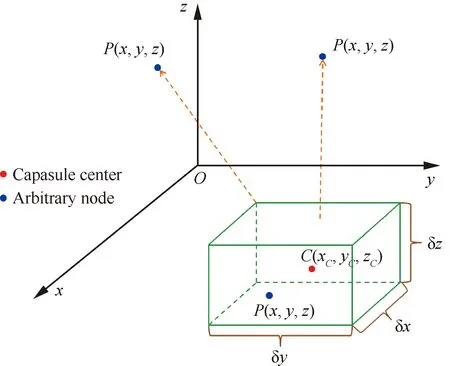
图9 定点和临界长方体的距离

图10 壁面距离计算的临界长方体算法
任意给定空间网格节点P,可以按照如下4个步骤在集合SolidNodeSeti中快速查找出最近的固壁节点:
步骤1依次计算当前网格节点到基础查询数据集中每个临界长方体的距离,其定义需要满足这样的条件:无论网格点在临界长方体内部还是外部,它与临界长方体的距离将小于到其中任意固壁节点的距离。记P到每个Capsules区域的距离为d(P,Capsules)。根据图9,设P的坐标为(x,y,z)、Capsules的格心坐标为(xC,yC,zC),那么,对于任意相对位置,d(P,Capsules)具有统一形式:
d(P,Capsules)=
(27)
式中:
f(ξ,η,ζ):=
(28)
为每个Capsules对象设置逻辑变量Logic表征其激活属性,初始值为TRUE;同时,初始化
d(P,SolidNodeSeti)=LARGE_DISTANCE
(29)
式中:LARGE_DISTANCE=1.0×1040。
步骤2在当前所有激活的临界长方体中进行遍历,选取使d(P,Capsules)达到最小值的Capsules。如果符合条件的Capsules存在,那么记录其编号s以及d(P,Capsules),此时最近的固壁点位于其中的可能性很大,为进一步确认,通过步骤3对临界长方体内的固壁点集进行更加详细的判断;否则,在激活状态的临界长方体不存在时,转向步骤4即可。
步骤3一边计算网格节点与固壁节点的距离,一边将其与处于激活状态的各个临界长方体的距离进行比较,如果后者大于当前的距离,那么其中的任意固壁节点皆不可能成为最近距离点,所以不再予以考虑,具体过程描述为:在Capsules覆盖的子集SubNodeSetis上,计算
d(P,SubNodeSetis)∶=
MinVal(d(P,Q)|Q∈SubNodeSetis)
(30)
令Capsules的逻辑变量Logic=FALSE且更新d(P,SubNodeSetis),即
d(P,SolidNodeSeti)=
min(d(P,SolidNodeSeti),d(P,SubNodeSetis))
(31)
遍历全部临界长方体,如果临界长方体Capsules满足条件
d(P,SolidNodeSeti) (32) 那么,为其逻辑变量赋值Logic=FALSE;最后,返回步骤2。 步骤4当步骤2和3的循环判断结束后,即可得到最终的壁面距离d(P,SolidNodeSeti)。 在网格组gpi上,结合距离初筛条件与覆盖初筛条件,定义查询节点的集合 QueryNodeSeti:={P|dt(P) Dj0∪Dj1∪…∪DjL-1} (33) 且QueryNodeSeti满足 NegNodeSeti⊂QueryNodeSeti⊂NodeSeti (34) 式中:源网格组gpi与目标网格组gpjs极小外部盒子参数可以在并行编程框架下实现共享,js∈{j0,j1,…,jT-1}为目标网格组的编号。 对于集合关系式(34),根据覆盖关系式(17)从QueryNodeSeti筛选出NegNodeSeti,在并行编程框架下的查询算法以及数据流如图11所示。 图11 节点查询算法及插值信息数据流 设当前源网格组SG各子网格块分布在编号连续的S个进程中,在每个进程上,子网格块将按照六维超子空间分割法[24]生成独立的二叉树结构,为任意外部节点提供快速查询服务;同时,按照式(5),根据延拓型物理边界,SG在每个进程内子网格块体单元被初步划分为一般单元与延拓单元。设SG的任意目标网格组为TG,因为查询节点分布在编号连续的T个进程中,每个进程对应查询节点的子集QueryNodeListjs。在非阻塞通讯模式下,主进程对QueryNodeListjs进行收集,即 QueryNodeSetj=QueryNodeListj0∪ QueryNodeListj1∪…∪QueryNodeListjT-1 (35) 然后将其共享到SG所在的进程组内进行查询操作,其步骤如下: 步骤1贡献单元的并行查找与插值信息的计算。在上述共享机制作用下,SG涉及的每个进程内皆包含目标网格组TG上查询节点集合QueryNodeSetj的完整信息。任意给定查询节点对象P∈QueryNodeSetj,通过局部二叉树查询算法,如果存在体单元velem∈GenElemSeti覆盖P,那么在对象P中记录如下3种信息:① velem所在的当前进程编号以及局部体单元序号;②P在velem中的相对坐标;③P到SG壁面的距离d(P,SolidNodeSeti)。由于已计算出velem各个节点到自身网格组的壁面距离参数ds,因此结合②中的相对坐标以及距离函数的空间连续性,即对d(P,SolidNodeSeti)进行三线性插值。如果当前进程内不存在体单元velem∈GenElemSeti覆盖P,那么擦除对象P在当前进程的全部信息。 步骤2贡献单元存在时节点的筛查。在SG涉及的每个进程内,剩余查询节点信息通过图11中的信息收集器collector汇总后,在TG包含的进程组内进行信息共享。在TG各子网格块所在的进程内,皆包含collector共享的有效查询结果。如果查询节点P原始的进程编号与当前进程一致,那么结合其局部节点编号,在当前进程网格块的相应位置更新信息:如果dt(P) 步骤4剩余查询节点的处理。在式(34)中,查询节点集包含了非激活点集,在确认阶段,排除所有的非激活点集后,剩余的查询节点P都需归入一般节点集合,即P∈GenNodeSetj。 主要对4种非结构体单元进行处理,即四面体、六面体、三棱柱和金字塔。为确定给定节点与体单元的相对位置,需要把物理坐标系下的体单元映射成为计算坐标系下的标准计算单元。图12展示了4种类型单元与标准单元之间的微分同胚关系,其中物理坐标系下体单元的覆盖区域可用形函数的线性组合加以描述: 图12 4种类型单元与标准单元之间的微分同胚关系 (36) 式中:(x,y,z)为体单元内部任意一点的物理坐标;(ξ,η,ζ)为对应的计算坐标;M为单元角点总数;(xs,ys,zs)为角点物理坐标。不同类型velem单元的形函数序列如表1所示。 表1 4种类型单元的插值形函数序列 为了确定给定节点P(x*,y*,z*)在标准计算单元中的相对坐标(ξ,η,ζ),建立非线性方程组 (37) 构造Newton迭代序列 (38) 式中:下标n与n+1用来区分当前时间层与更新时间层的变量。设收敛结果(ξ,η,ζ)满足条件: 那么,可以得到P∈velem的结论。 至此,已实现网格节点分类算法的并行化工作。在上述“初筛+确认”模式中,基于两种距离参数以及网格组极小外部盒子参数对可疑节点的筛查,使各进程内查询节点集合的规模得到了有效的控制;同时,对于目标网格组TG来说,伴随着洞内节点的不断剔除,它在与另一组网格组SG进行配对时,查询节点的总量将进一步的缩小。这些措施都极大降低了并行通讯的压力。 根据第1节的介绍,在完成网格节点分类的基础上,可以结合单元与节点的拓扑关系,完成场单元、洞内单元以及重叠单元的划分。在2.3节描述的单元分类过程中,第1)2)4)步可以在各自进程内通过“节点-单元染色”方式独立进行。然而,在第3)步中,与过渡单元相邻的非活跃单元被定义为一般性重叠单元;如果过渡单元与非活跃单元的分界面与网格分区边界面存在重合(如图13所示),那么需要通过分区边界处点对点的并行通讯完成单元类型信息的传递,其算法流程如图14所示。 图13 过渡单元与非活跃单元分界面与网格分区边界面重合情况 在图14所示的各个进程内,沿着箭头指向,重叠单元识别算法的并行化共分为5个步骤:① 根据网格节点的激活属性将体单元划分为活跃体单元、非活跃体单元、过渡体单元与延拓型重叠单元4种类型;② 对过渡体单元包含的网格节点(称为过渡节点)进行染色标记;③ 在当前进程内,根据已染色的过渡节点识别一般类型重叠单元与洞内单元;④ 根据网格分区边界处的并行通讯,识别一般型重叠单元;⑤把一般型重叠单元与延拓型重叠单元统一归并到重叠单元集合中,活跃体单元与过渡体单元统一归并到场单元集合中。 图14 重叠单元的并行识别过程 图15展示了使用二叉树技术建立重叠单元格心与贡献体单元之间“插值-覆盖”映射的过程。图15与图11有较高的相似度,特别是在网格节点分类(即并行化自动挖洞)时使用的二叉树结构未发生变化。此处主要有2点不同:① 目标网格组上收集的节点信息变更为重叠单元格心信息;② 在源网格组上,二叉树查询算法对应的有效贡献单元附加约束属性由一般型单元变更为场单元。有效贡献单元的约束条件,有效避免了不同网格组重叠单元互相插值的异常现象,从而使流场迭代过程顺利进行。 图15 重叠单元的并行装配 本文采用面向对象编程思想,使用C++语言和MPI并行编程模型实现了重叠网格隐式装配算法的并行化,从而建立了图16所示的“重叠网格缝纫机”(Overlapping Grid Sewing Machine, OGSM)工具库。 图16 OGSM运行流程 OGSM描述的流程共分为8个节点,它们分别是:① 读入当前进程子区域的网格拓扑信息;② 建立网格分区边界的并行通讯架构;③ 自动化注册网格组重叠关系;④ 基于壁面距离准则识别重叠单元;⑤ 在背景网格上查找重叠单元的最优贡献单元;⑥ 重叠装配信息的跨进程整理;⑦ 统 计当前进程内子区域上贡献单元的总数;⑧ 输 出重叠插值以及单元分类信息。其中,左侧(蓝色)方框表示的是OGSM的外部接口,右侧(绿色)方框内是重叠网格并行装配算法的内部实现。 为了独立测试OGSM的并行装配能力,对包含5个球体部件的重叠网格进行装配。如图17所示,每个球体部件独立生成非结构网格,体单元总量为1.2亿。在z=0平面内进行切割,可以看到5个区域之间的自动装配结果。其中,蓝色曲线为网格分区边界,绿色部分为重叠单元。在该算例中,部件网格的外延拓边界与挖洞边界相交,球体之间的挖洞边界遵循了壁面距离准则,本文的自动挖洞逻辑的准确性得到了检验。图18展示了算法的并行效率曲线,随着分区进程数的增加,装配时间单调下降。 图17 重叠单元和场单元切片(截面方程:z=0) 图18 不同进程对应的墙上时间 为了进一步检验OGSM重叠单元与贡献单元插值关系的准确性,本文通过接口模式将其嵌入至流场求解器PMB3D[25]中,对WPFS(Wing-Pylon-Finned Store)投放算例的非定常流场进行了数值模拟。 WPFS模型[26]是美国发起的用于CFD验证的机翼外挂物分离投放简化模型,其中单外挂物分离投放试验由AEDC于1990年完成,该模型作为标准算例通常用于对外挂物分离数值方法进行考核。如图19所示,研究模型的机翼为45°后掠的三角翼,采用NACA64A010翼型,无扭转。外挂物的头部为尖拱形,中间为圆柱,共有4片尾翼,呈X形分布。尾翼采用NACA0008翼型。外挂物质心位置距头部顶点1.417 3 m,参考长度0.508 m,参考面积0.202 69 m2。实验模拟研究两个状态下的投放分离,状态1的环境高度为7 925 m(26 000 ft),来流马赫数0.95;状态2的环境高度为11 582 m(38 000 ft),来流马赫数1.2,机翼无攻角和侧滑角。为了确保外挂物安全分离,在投放初始瞬间,加入了两点弹射力的作用,弹射力1的作用点距头部尖点1.24 m,大小10 679.4 N,弹射力2距头部尖点1.75 m,大小42 717.5 N。在外挂物离开载机0.1 m(分离时间0.055 s)以后,弹射力消失。图19中给出了外挂物的质量以及3个方向上的转动惯量,由于外挂物关于轴和轴对称,它的惯性积Ixy=Iyz=Izx=0 kg·m2。 图19 外挂分离试验模型参数 WPFS算例中,在机翼和弹体部件周围生成多块结构网格,前者对应的节点总数和体单元总数分别为5 124 792和4 798 080,后者对应的节点总数和体单元总数分别为1 722 242和1 585 664。整个计算区域划分到64个进程中。在每个进程上,合并重合的节点单元和面单元,多块结构网格即转化为独立的非结构网格(原有各个网格块可以是不连通的)。使用OGSM进行重叠装配后,依旧采用多块结构网格求解器进行RANS方程的非定常数值模拟,其中对流项和黏性项分别使用Roe格式和SA湍流模式进行离散,时间方向上采用双时间步推进,结合minmod限制器抑制非物理解的生成。 在双时间步推进过程中,流场求解器PMB3D的每个物理迭代步划分为300个子迭代步,单个子迭代步消耗的时间为1.49 s;因为弹体相对于机翼处于不同位置时,依据壁面距离准则得到的挖洞边界形态各不相同,从而导致重叠装配时间发生一定的变化,所以本文仅选取初始时刻对OGSM模块的装配时间进行统计,对应的装配时间为9.29 s,占每个物理迭代步消耗时间的比率为2.1%,能够满足当前算例的数值模拟需求;同时,壁面距离的计算时间为3.12 s,可疑查询节点的并行确认时间为4.63 s,它们与总装配时间的比率分别为33.5%和49.9%;相比之下,生成背景网格二叉树的时间为0.22 s,重叠单元插值系数的并行计算时间为0.69 s,它们与总装配时间的比率仅为2.3%和7.4%。结合本文的算法流程可以判断,随着进程数的增加,切割盒子序列的结构未发生明显变化,为适应壁面节点规模不断增加的情形,今后需对壁面距离的高效并行算法做更加深入的研究;同时,基于部件网格的几何特征,挖掘新的初筛判据,在早期排除更多的待查询节点,也有助于进一步降低并行通讯压力,从而提升OGSM的装配效率。 图20给出的是状态1(Ma=0.95)外挂物表面压力系数Cp和空间流线,可以看到初始时刻外挂物受到来流外洗的作用,产生向右的偏航力矩。在该算例中,机翼为前缘后掠角45°的三角翼,从翼根开始,气流在受到机翼的阻滞作用后,产生沿横向流动的速度分量。低于外挂物来说,头部靠机翼内侧的地方迎着横向流动,压力系数较另一侧高,因此产生头部向机翼外侧方向偏转的偏航力矩。 图20 外挂物表面压力系数和空间流线分布 图21显示的是外挂物处于挂载状态时展向截面马赫数云图,机翼上下表面大部分区域都是超声速流动,靠近机翼后缘的地方,上下表面均形成了激波,波后流动速度为亚声速。图21同时给出了截面上的网格分布,从中能够清晰地看到重叠边界的位置,在跨过重叠边界的地方,压力系数云图分布连续,反映了在这些地方流场信息得到了正确的传递。 图21 外挂物处于挂载状态时展向截面马赫数云图 图22给出的是外挂物分离轨迹示意图,其中模拟时长t为0.5 s。从图中可以看到,外挂物在分离过程中,产生了头部向机翼外侧的偏航运动;在俯仰方向上,分离初始阶段产生的是抬头运动,随后在尾翼的稳定作用下产生低头运动。图22反映了外挂物分离过程的总体运动趋势,定性地描述了运动过程,下面将给出定量描述。 图22 外挂物分离轨迹 图23和图24分别给出的是外挂物质心位置(dx、dy、dz)和线速度(U、V、W)变化曲线,可以看到在重力和弹射力作用下,外挂物向机翼下方移动,其运动幅度在3个方向上是最大的;同时在阻力作用下,外挂物向机翼的后方移动;在横向方向上(y方向),外挂物先是向机翼的内侧移动,然后在t=0.35 s以后,外挂物开始向机翼外侧移动,尽管移动幅度较小,计算仍比较准确地模拟这种变化趋势。总的来说,在所显示的时间范围内(t=0.5 s),计算得到的质心线速度和位移和实验值都比较吻合,稍显不足的是由于黏性计算的阻力大于试验值,所以模拟得到的后向移动速度略大。 图23 外挂物质心位置变化曲线 图24 外挂物线速度变化曲线 图25和图26分别给出的是外挂物的姿态角和角速度的时间历程,其中P、Q、R分别为体轴系的3个角速度分量,Φ、Θ、Ψ分别为滚转角、俯仰角和偏航角,用来表示从地轴系到体轴系的变换。对于俯仰运动来说,在分离初始阶段,弹射力产生较大的抬头力矩,弹射力维持的时间到t=0.055 s, 之后弹射力作用消失,作用在外挂物上的气动力和力矩开始起主导作用,这时候气动力产生的是低头力矩,在t=0.2 s以后,外挂物开始下俯运动,本文计算的最大俯仰角度和下俯开始位置都和试验值吻合良好。在偏航方向,从分离开始外挂物偏向机翼的外侧,在t=0.5 s偏航角约为16°,在t≤0.4 s计算的偏航角与试验值吻合良好,t>0.4 s后开始出现偏差,影响到后续计算的正确性。在滚转方向,分离后外挂弹体向机翼外侧滚转,在t=0.5 s之前滚转角的计算和试验值比较一致,由于x方向的转动惯量较小(比其他两个方向小1个量级),气动力估计的误差很容易在这里得到放大,从而对计算结果造成污染。 图25 外挂物姿态角随时间变化情况 图26 外挂物角速度随时间变化情况 结合数值模拟方法,本文认为空间离散和时间离散的误差来源于如下3个方面:① 重叠网格隐式装配算法中,为简明计,沿着挖洞边界仅延拓了一层重叠单元,各部件网格间的物理信息交换量略显不充分;② 双时间推进过程中,限制器造成的数值解污染在一定程度上得以累积,影响了后期数值模拟的精度;③ SA湍流模型经验参数的选取欠佳,影响了RANS方程黏性项的离散精度。今后需继续研究重叠边界附近的高精度插值技术;同时,不断提高流场解算器的离散精度,从而在整体上降低CFD仿真过程中产生的误差。 本文基于网格节点的壁面距离参数,构造了一种自动化的并行重叠网格隐式装配算法,同时使用集合论对该算法的并行化过程进行了详细地描述。网格组极小内部-外部盒子、盒子切割方法、初筛+确认两步分析法、二叉树排序-查找等技术的综合运用,降低了重叠装配算法的并行通讯压力,使之能够适应多体相对运动时复杂非定常流场的数值模拟。数值计算结果表明,该重叠装配算法具备了较高的计算效率与鲁棒性,能够辅助实现针对外挂物分离的非定常流场准确模拟。 下一步工作内容包括两方面:一是将自适应笛卡尔网格融入到当前的重叠装配框架中,进一步拓展其工程应用范围;二是继续优化初筛技术,提升大规模重叠网格的并行装配效率。




2.4 重叠单元的识别及并行化装配

3 算例验证

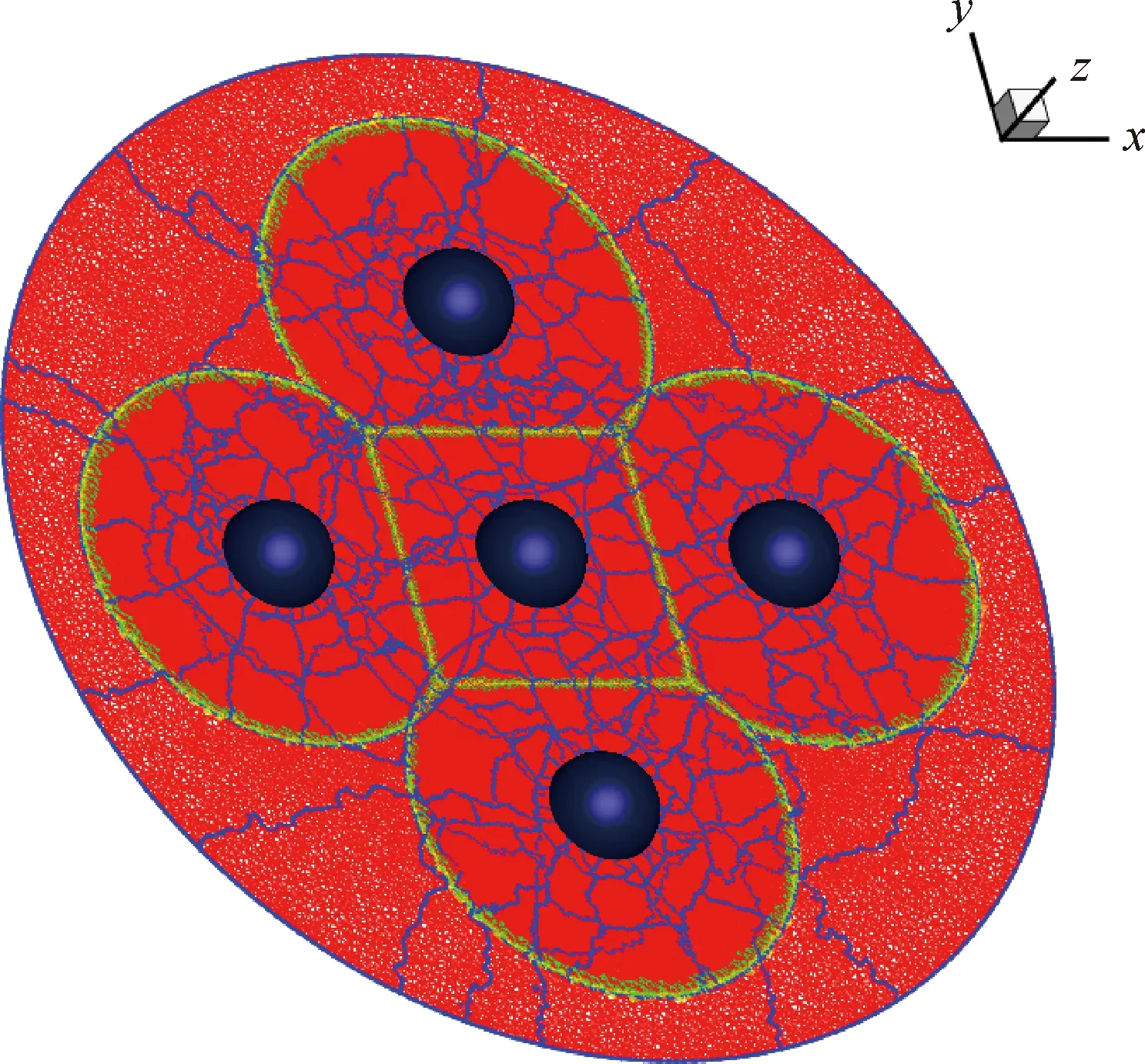
3.1 五球体部件

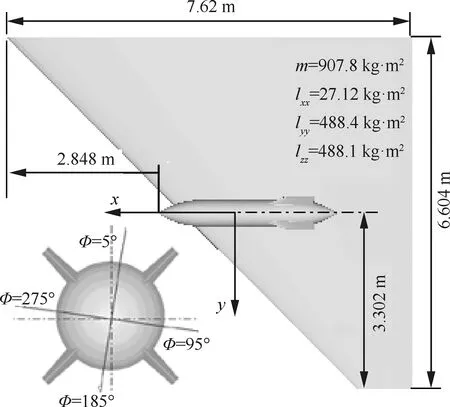
3.2 WPFS模型







4 结 论
