基于超材料的太赫兹分波器的研究

张雪雯，潘 武，沈 涛，李 燚

〈太赫兹技术〉

基于超材料的太赫兹分波器的研究

张雪雯，潘 武，沈 涛，李 燚

（重庆邮电大学 光电工程学院，重庆 400065）

本文提出了一种基于超材料的太赫兹分波器，其结构单元由上下两层“一”字型金属线以及中间的石英介质构成。此分波器工作在太赫兹通信窗口，将中心频率为0.225THz和0.300THz的两束太赫兹波分离，其隔离度分别为34dB、47dB，插入损耗分别为0.19dB、0.04dB，分波器的群延迟稳定。另外，也对分波器的等效参数以及结构参数变化进行了仿真分析。结果表明，所设计的太赫兹分波器具有插入损耗小、隔离度大、群延迟稳定等特点，且性能指标受参数变化的影响较小，在太赫兹通信系统中具有较好的应用前景。

太赫兹；分波器；超材料

0 引言

太赫兹通信因其具有频谱资源带宽宽、传输时延低、通信容量大等优势而备受关注，是未来6G移动通信系统极具前景的宽带通信技术[1-2]。为了有效地提高太赫兹波带宽利用率，增大容量，灵活组网，在太赫兹通信系统中开展波分复用技术的研究具有必要性和现实意义[3]。合波器（复用器，Multiplexer）和分波器（解复用器，Demultiplexer）是波分复用系统的重要器件[4]。在太赫兹频段内，目前复用及解复用器件的研究还很少，并且主要集中在基于光子晶体的太赫兹分波器的研究[5]。

2015年，Li Jiusheng[6]提出了一种基于光子晶体的四通道分波器，最后输出了0.585THz、0.537THz、0.560THz和0.524THz四种波长的太赫兹波，其插入损耗分别为0.127dB、0.285dB、0.313dB和0.399dB，信道的隔离度分别为12dB、11dB、13dB和22dB，此分波器只有一个信道的隔离度大于20dB。2016年，Li Shaopeng[7]提出了光子晶体太赫兹波分复用器，该器件在1.07～1.16THz的频率范围内有3个传输峰，分别为1.09THz、1.12THz和1.13THz，其插入损耗分别为1.92dB、0.96dB以及1.93dB，此分波器有两个通道的插入损耗都大于1.5dB。近几年基于光子晶体的太赫兹分波器的隔离度大多都在15dB左右，在实际通信系统中，分波器的隔离度要求最小应大于22dB，并且要求插入损耗小于1.5dB[8]，所以太赫兹分波器的隔离度有待提高并且插入损耗有待减小。光子晶体加工困难、价格昂贵，不利于大批量的生产和应用[9]，而超材料相对于光子晶体来说，更易于加工。本文主要研究基于超材料的太赫兹分波器，为太赫兹波分复用器件的研究提供一个新的方向。

1 超材料分波器

超材料的单元结构是亚波长尺寸，即可看成均匀介质。均匀分层介质中的介电层可以用传输线模型进行建模[10]。如图1所示，超材料与自由空间构成传输线网络。从太赫兹波入射方向看，传输线网络的输入阻抗为超材料，特征阻抗为自由空间。

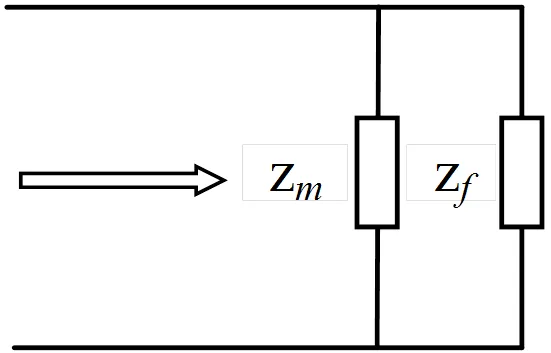
图1 超材料等效传输线模型

对于TM波而言，反射系数与透射系数可表示为：

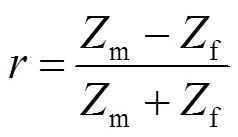
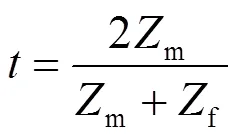
式中：m为超材料阻抗；f为自由空间阻抗。(1)式中，当m＝f时，即自由空间阻抗与材料的阻抗匹配时，反射波达到最小值[11]。(2)式中，当m＝0时，＝0。超材料的等效阻抗与自由空间阻抗进行归一化表示为：

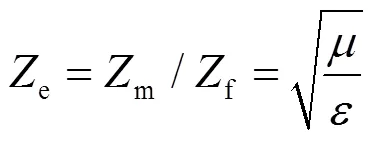
若阻抗匹配，则超材料归一化阻抗的实部为1，虚部为0[12]。(3)式中为等效介电常数，为等效磁导率。若用等效电路相关参数来表示超材料的等效阻抗，则超材料表面等效阻抗：

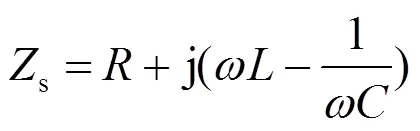
谐振频率则为：

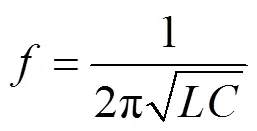
式中：、分别为等效电感和等效电容，当超材料表面金属层的尺寸发生变化时，等效电感和电容会相应地变化，从而等效阻抗发生变化。由于超材料的等效参数取决于单元结构，想要改变超材料的性质，则需要对单元结构进行调整。

利用超材料实现分波功能，需要将两种频率的太赫兹波在空间上分开，以达到分波的目的。图2(b)为超材料分波器的示意图，当1和2两种频率的太赫兹波在面内同时入射到超材料表面时，假设1反射，接收反射波1的端口为port 1；2透射，接收透射波2的端口为Port 2。以Port 1为例，超材料分波器的隔离度与插入损耗的计算式为：

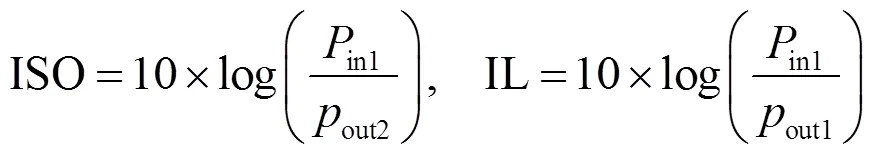
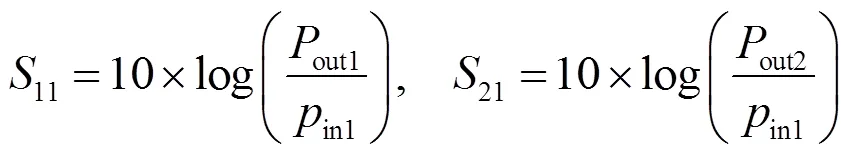
式中：in1与out1分别为Port1的输入功率与接收端Port 1的输出功率，out2为1泄漏到Port 2的功率，隔离度和插入损耗可表示为：

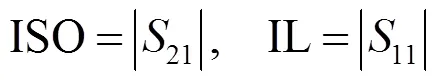
图2(a)为超材料分波器单元结构图。图2(b)为超材料太赫兹分波器截面图。(c)为超材料太赫兹分波器的单元结构尺寸示意图。上层金属图案与下层金属图案一致，都为“一”字型金属，长＝458mm，宽＝16mm，顶层和底层的金属材料是金（电导率：4.56×107S/m），介质层是石英（相对介电常数：3.75），厚度为＝50mm，超材料单元周期＝600mm。图2(d)为超材料阵列的结构示意图，太赫兹波入射在面内。

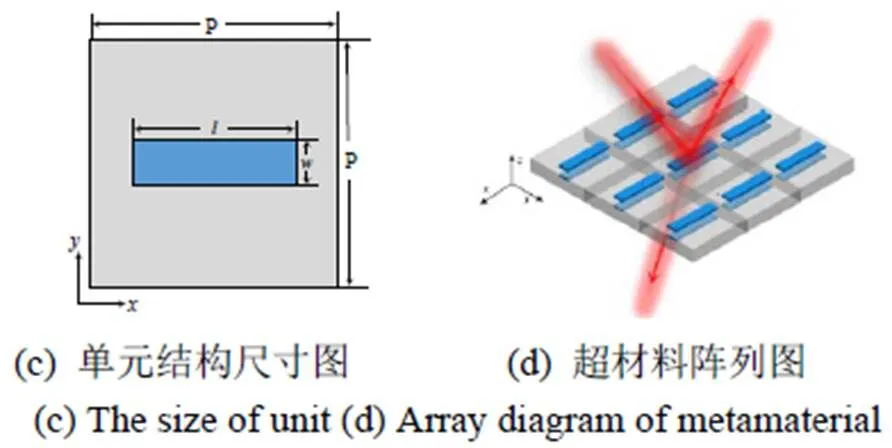
图2 超材料分波器结构示意图

2 仿真与分析

利用CST软件对此结构进行仿真，入射太赫兹波为TM模式，法线方向为，太赫兹波入射方向与轴的夹角为10°，反射角为，透射角为，如图2(b)所示。图3为分波器的S参数曲线仿真结果：在1（0.222～0.228THz）范围内，分波器的隔离度均大于22dB，在0.225THz处的隔离度最大为34dB，插入损耗为0.19dB。在2（0.291～0.312THz）范围内，分波器的隔离度均大于22dB，在0.300THz处的隔离度最大为47dB，插入损耗为0.04dB。此分波器对于上述两个频段范围内的隔离效果都较好，并且插入损耗较小，利于通信信号的有效传输。

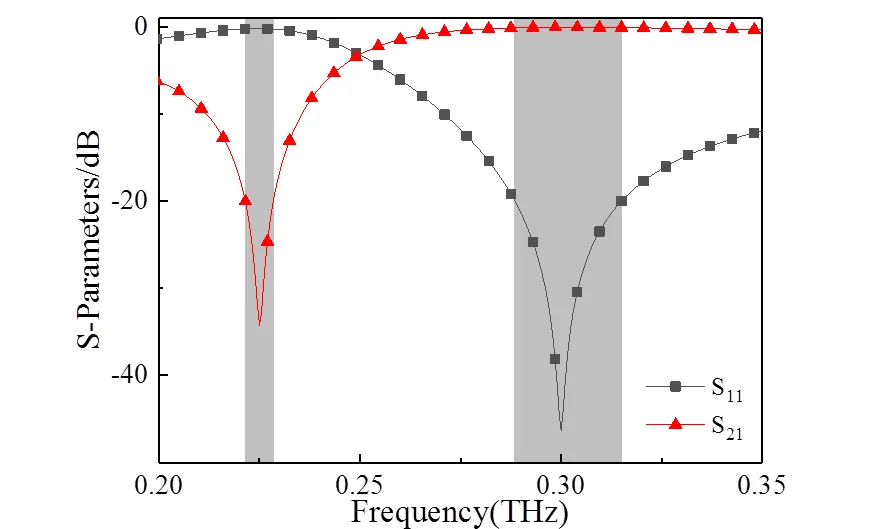
图3 分波器S参数曲线仿真结果图

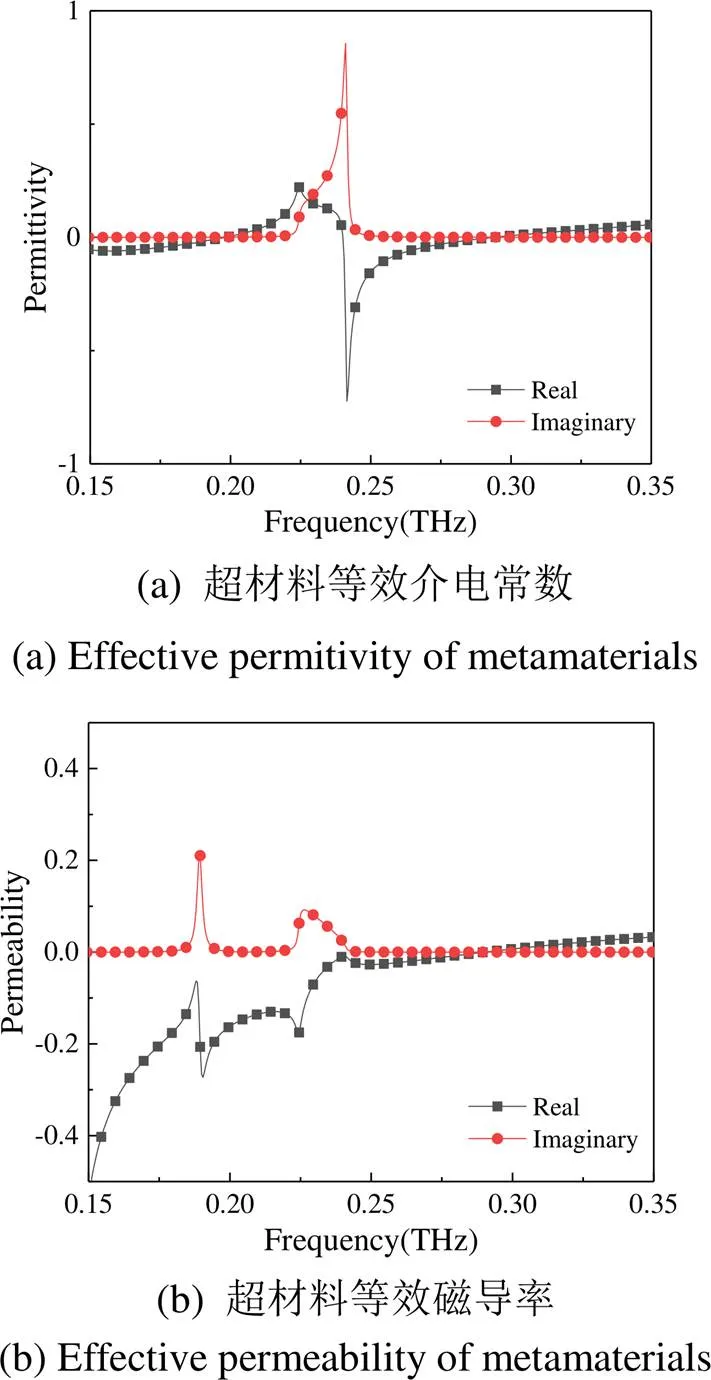
为了探究超材料的谐振特性，将得到的S参数进行参数反演，超材料的等效参数如图4所示，其中(a)(b)(c)分别为等效介电常数、等效磁导率以及等效阻抗。

图4(a)中在频率0.220～0.250THz范围内发生了电谐振[13]。相同频段内，(b)并无谐振现象，因此在0.225THz处发生的谐振是由电谐振引起的。在0.300THz处，并无任何谐振存在，介电常数和磁导率虚部均为0，并且实部相等，即＝，可得e＝1，在0.300THz的阻抗实部为1虚部为0，满足阻抗匹配条件，此时反射波达到最小。

群延迟表征不同频率信号产生的时间延迟，采用固定相位近似的方法，利用相移对角频率求导[14]，若是通带内群延迟的差异过大则会引起信号失真[15]，因此，通带内群延迟差异越小越好，理想状态下，群延迟为一个固定的常数。

针对群延迟现象，分别仿真计算了上述两个端口所在的工作频率范围内的群延迟，图5(a)为Port 1的群延迟仿真结果。在Port 1处，群延迟平均值为6.74ps，群延迟最大差值为0.44ps。(b)则为Port 2群延迟仿真结果，在Port 2处，群延迟随着频率的增高而缓慢递减，平均值为3.61ps，群延迟差值的最大值为1.84ps。未来6G的通信延迟估计为0.1ms[16]，而从上述两个端口的群延迟数据可以看出，在1与2的工作频率范围内，太赫兹分波器的群延迟差值小，较为稳定。

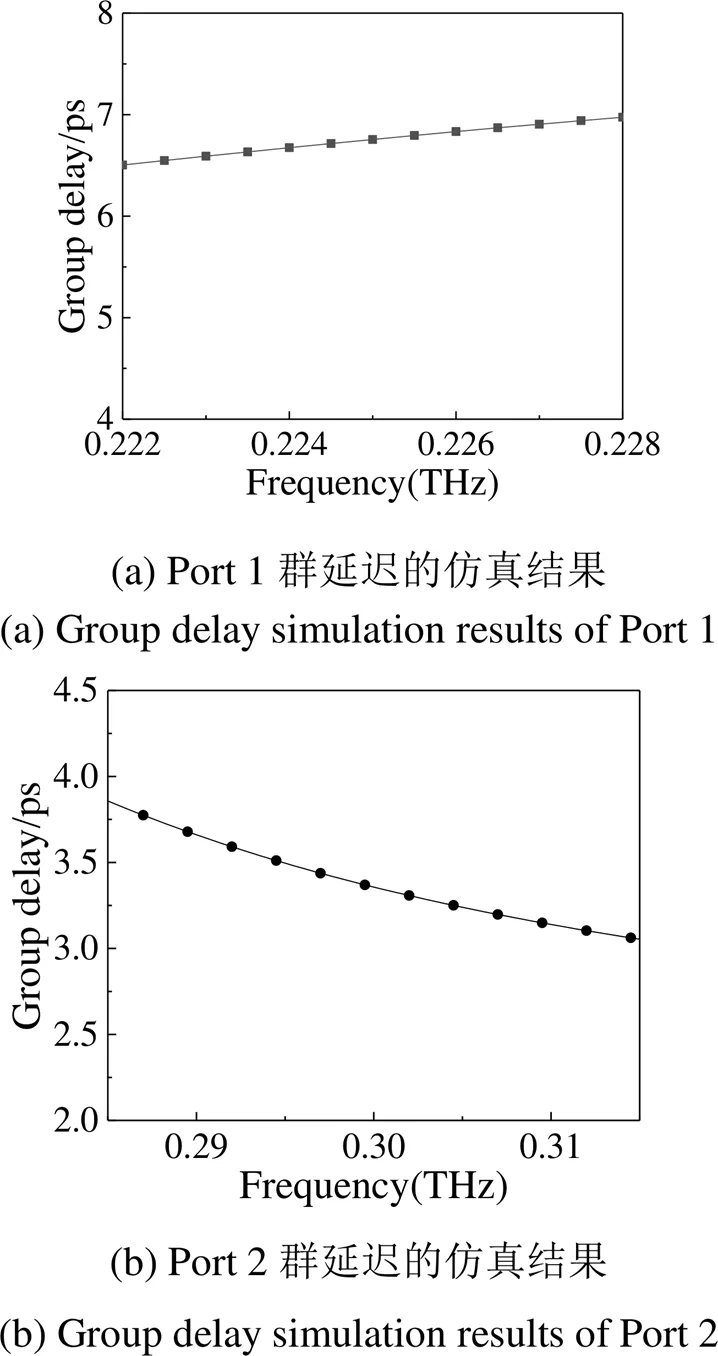
图5 分波器工作频段内群延迟

3 结构参数对分波器性能的影响

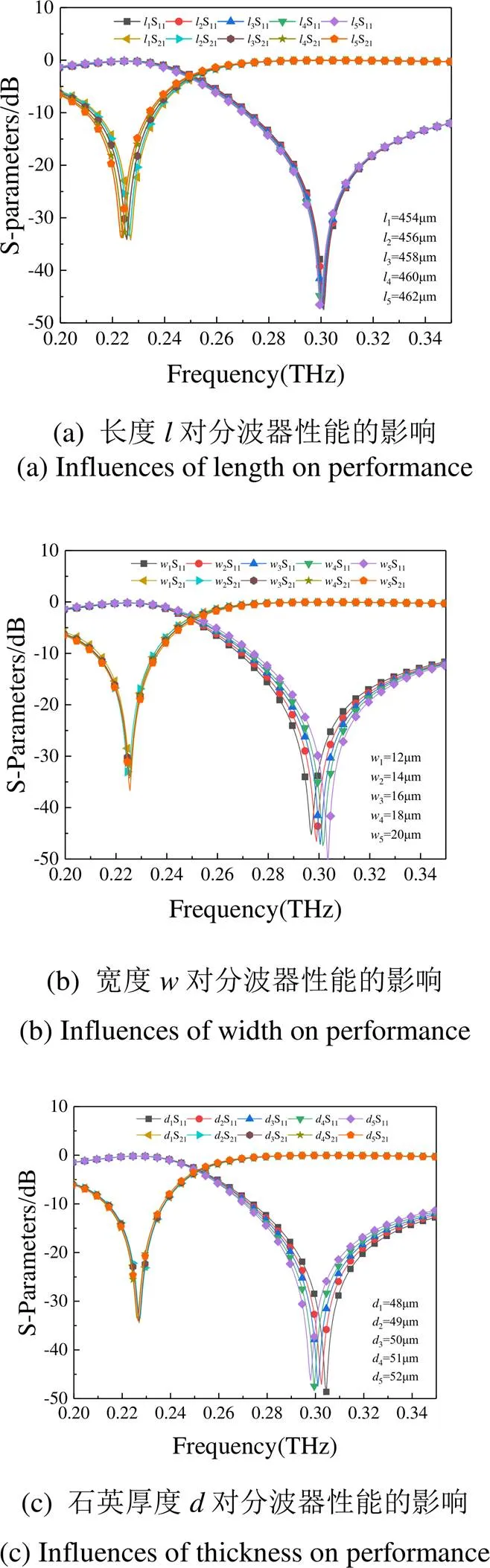
为了探究太赫兹分波器的相关尺寸参数的变化对太赫兹分波器的性能的影响，在其他条件保持不变的情况下，分别改变双层金属长度、金属线宽、石英介质厚度以及双层金属条的相对位置并在CST中仿真。

图6为结构尺寸对分波器性能的影响。图(a)(b)(c)分别表示金属条长度、宽度、以及介质厚度参数的变化对S参数曲线的影响。双层金属短截线结构[17]的等效电感主要由短截线的自感决定，数值表示为＝(/)，等效电容主要由层间电容决定，数值表示为＝/。上文中提到了谐振频点与等效电容、电感有关，根据上述表达式，即可推导相关参数变化与谐振频点的关系。透射曲线的频移只与有关，并且与成反比[18]，所以透射曲线红移。另外，从上图也可以看出，宽度变化对于反射曲线更为敏感，随着宽度增加，反射曲线蓝移。并且反射曲线的变化与介质厚度成反比，厚度越大，反射曲线红移。为了探究上下面金属条不对准对超材料性能的影响，图(d)为上下面金属条在面内向轴方向平移的相对距离后的S参数曲线，发现金属条不对准对于透射和反射曲线几乎无影响。

4 结论

本文首先讨论了现有太赫兹分波器的待改进的方面，提出了基于超材料的太赫兹分波器。该分波器工作在太赫兹大气窗口附近，在两个工作频率范围的中心频率处，其隔离度分别为34dB和47dB，插入损耗分别为0.19dB和0.04dB。通过S参数反演的方法得到了超材料分波器的等效参数。随后计算了太赫兹超材料分波器的群延迟，可以看到两个端口的群延迟均变化较小，保证了信号的不失真传输。最后讨论了结构参数对分波器性能的影响。结构参数的变化仅会使两个端口的工作频段产生微小频移，对插入损耗和隔离度均没有明显影响，因此本文提出的太赫兹超材料分波器有望能应用于未来的太赫兹通信系统中。

[1] 赵亚军, 郁光辉, 徐汉青. 6G移动通信网络：愿景、挑战与关键技术[J]. 中国科学: 信息科学, 2019, 49(8): 963-987. ZHAO Yajun, YU Guanghui, XU Hanqing. 6G mobile communication network: vision, challenges and key technologies[J].:, 2019, 49(8): 963-987.

[2] 陈亮, 余少华. 6G 移动通信发展趋势初探[J]. 光通信研究, 2019, 45(4): 1-2. XU Liang, YU Shaohua. Preliminary study on the development trend of 6G mobile communication[J]., 2019, 45(4): 1-2.

[3] 莫秋燕, 吴家隐. 波分复用系统的研究综述[J]. 信息通信, 2019(7): 191-192. MO Qiuyan, WU Jiayin. Review of research on wavelength division multiplexing system[J]., 2019(7): 191-192.

[4] 孟宪浩. 密集波分复用系统中合波器/分波器的测试[J]. 电气化铁道, 2002(1): 41-42. MENG Xianhao. Test of multiplexer/demultiplexer in dense wavelength division multiplexing system[J]., 2002(1): 41-42.

[5] Yata M, Fujita M, Nagatsuma T. Photonic-crystal diplexers for terahertz- wave applications[J]., 2016, 24(7): 7835-7849.

[6] LI Jiusheng, HAN L, LE Z. Compact four-channel terahertz demultiplexer based on directional coupling photonic crystal[J]., 2015, 350: 248-251.

[7] LI S, LIU H, SUN Q, et al. Multi-channel terahertz wavelength division demultiplexer with defects-coupled photonic crystal wave guide[J]., 2016, 63(10): 955-960.

[8] Telecommunication Standardization Sector of ITU. Series G: Transmission Systems and Media, Digital Systems and Networks: ITU-T G695 [S]. 2018.

[9] 丁涛, 刘占芳, 宋恺. 三维光子晶体的制备[J]. 化学进展, 2008, 20(9): 1283-1293. DING Tao, LIU Zhanfang, SONG Kai. Fabrication of three- dimensional photonic crystals[J]., 2008, 20(9): 1283-1293.

[10] ZHANG L, ZHANG S, LIU Y, et al. Broadband tunable frequency selective surface for steerable antenna applications[J]., 2016, 64(12): 5496-5500.

[11] Osipov A V. Minimum reflection properties of planar impedance- matched boundaries[J]., 2014, 62(11): 5666-5670.

[12] Lim J H, LIU T, Kim S S. Numerical analysis of complex impedance and microwave absorption of metamaterials composed of split cut wires on grounded dielectric substrate[J]., 2014, 117(3): 1401-1407.

[13] XIONG X, SUN W H, BAO Y J, et al. Switching the electric and magnetic responses in a metamaterial[J]., 2009, 80(20): 2665-2668.

[14] Stojanović D B, Radovanović J, Milanović V. Influence of the geometry of terahertz chiral metamaterial on transmission group delays[J]., 2016, 48(4): 272.

[15] 白胜元, 顾培夫, 刘旭, 等. 波分复用薄膜干涉窄带滤光片的设计[J]. 光学仪器, 2001(Z1): 114-119. BAI Shengyuan, GU Peifu, LIU Xu, at el. Design of WDM thin-film interference narrowband filter[J]., 2001(Z1): 114-119.

[16] Piran M J, Suh D Y. Learning-driven wireless communications, towards 6G[C]//2019,(ICCECE), 2019: 219-224.

[17] Wakatsuchi H, Paul J, Greedy S, et al. Cut-wire metamaterial design based on simplified equivalent circuit models[J]., 2012, 60(8): 3670-3678.

[18] MIN L, HUANG L. Perspective on resonances of metamaterials[J]., 2015, 23(15): 19022.

Research on Terahertz Band Demultiplexer Based on Metamaterials

ZHANG Xuewen，PAN Wu，SHEN Tao，LI Yi

(,,400065,)

This paper proposes a terahertz demultiplexer based on metamaterials; its unit cell is composed of two layers of "one" shaped metal wires and a quartz substrate in the middle. The terahertz demultiplexer works in the terahertz communication window and demultiplexes two beams of terahertz waves with center frequencies of 0.225THz and 0.300THz. The isolation of the terahertz demultiplexer is 34dB and 47dB, and its insertion loss is 0.19dB and 0.04dB, respectively. The group delay of the demultiplexer was relatively stable. Finally, the influence of the effective and structural parameters of the demultiplexer on its performance are discussed. This terahertz demultiplexer has low insertion loss, large isolation, and stable group delay, and its performance is less affected by parameter changes. It has significant application prospects in practical terahertz communication systems.

terahertz, demultiplexer, metamaterial

TN304.12

A

1001-8891(2021)06-532-05

2020-06-09；

2020-10-22.

张雪雯（1996-），女，陕西宝鸡人，硕士研究生，现主要从事太赫兹超材料分波器研究。E-mail：zxw0115@163.com。

潘武（1966-），男，四川大英人，教授，现主要从事太赫兹技术、超介质材料研究。E-mail：panwu@cqupt.edu.cn。

重庆邮电大学新方向培育计划项目（A2014-116）。