一种FH-OFDM信号DCT-ACE联合优化抑制峰均比方法
2021-07-06田秉禾姜月秋
周 帆,田秉禾,刘 博,姜月秋
(沈阳理工大学 信息科学与工程学院,沈阳 110159)
跳频正交频分复用(Frequency Hopping-Orthogonal Frequency Division Multiplexing,FH-OFDM)是一种将跳频技术与正交频分复用技术相结合的复合通信系统,该系统兼具高数据率、高频带利用率以及极强的抗干扰能力,被广泛应用在信息化弹药、卫星通信和无人机通信等诸多领域。然而,考虑到FH-OFDM信号的多子载波性,当频域数据同相时,经逆快速傅里叶变换(Inverse Fast Fourier Transform,IFFT)处理后的时域信号会产生明显的峰值[1]。在接收端通过非线性放大器放大后,FH-OFDM信号的峰值进一步提高,并可导致信号发生畸变,进而影响信号的准确接收。
近年来,针对FH-OFDM信号峰均比(Peak to Average Power Ratio,PAPR)抑制问题的研究相对较少,其主要思想来源于对OFDM信号的PAPR抑制方法。抑制OFDM信号PAPR的基本算法大体可分为失真类和无失真类,如文献[2]采用动态星座图扩展法(Active Constellation Extension,ACE),文献[3]采用离散余弦变换法(Discrete Cosine Transform,DCT),均可在一定程度上实现对OFDM信号PAPR的抑制。但ACE算法要求更高的迭代次数,DCT算法收敛速度慢,二者不能适应通信系统时效性的要求[2-3]。为更好地解决FH-OFDM信号抑制PAPR过程中的时效性问题,立足于传统的离散余弦变换和动态星座图扩展法,将两者相融合并利用离散余弦变换矩阵正交性去相关性的特点,本文提出DCT-ACE联合优化抑制PAPR方法,该方法与传统ACE算法相比,在相同迭代次数条件下可改善PAPR的抑制效果;与传统DCT算法相比,可有效提升PAPR的收敛速度。
1 FH-OFDM信号工作机理
OFDM第k个符号表达式为
(1)
式中:N为子载波数;j为虚部;ai为进行IFFT前的频域符号,以a表示频域符号向量,即
a=(a0,a1,…,aN-1)T
(2)
以Ak表示快速傅里叶变换(Fast Fourier Transform,FFT)向量,即
Ak=exp(j2πki/N)
(3)
则OFDM信号可进一步表示为
s(k)=Aka
(4)
设编码向量为C(k),跳频信号等价于对频域符号a进行编码。因此,FH-OFDM信号可表示为
f(k)=A(k)C(k)a=s(k)C(k)
(5)
设c(i)为子载波跳频序列,将式(1)代入式(5)后进一步得到FH-OFDM信号的数学表达式为
0≤k≤N-1
(6)
FH-OFDM信号工作机理如图1所示[4-5]。
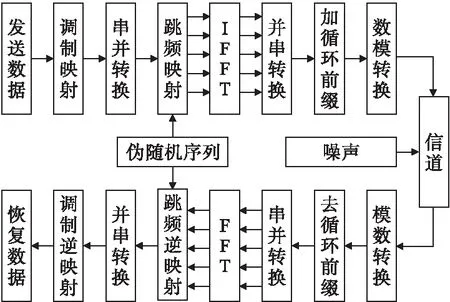
图1 FH-OFDM信号工作机理
2 DCT-ACE联合优化算法
2.1 离散余弦变换法
离散余弦变换法是一种可有效降低信号相关性的算法,其基本思想是利用离散余弦变换矩阵的正交性,在一定范围内实现对信号能量的集中化处理[6-7]。
设M表示矩阵的大小,m表示矩阵的行,n表示矩阵的列,则DCT矩阵可表示为
(7)
进一步设信号源对应的矩阵为[α0,α1,…,αn],则经过DCT矩阵处理后的信号可表示为
Φm=[α0,α1,…,αn]·D(m,n)
(8)
其中
(9)
由式(9)可知,采用余弦函数会使基带数据能量集中到某几个值上,利用该特性调制FH-OFDM信号,使信号能量集中在某几个子载波上,从而达到降低PAPR的目的[8-9]。结合式(6)可得经DCT变换后的FH-OFDM表达式为
0≤k≤N-1
(10)
2.2 DCT-ACE联合优化算法
DCT-ACE联合优化算法工作原理如图2所示。

图2 DCT-ACE联合优化算法原理框图
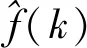
(11)

0≤k≤N-1
(12)
3 仿真验证与分析
3.1 仿真参数
由FH-OFDM信号产生机理可知,以1000个FH-OFDM符号为仿真对象,选取Matlab为仿真工具。设单个OFDM符号持续时间为93.7μs,一个符号包含80个比特(含循环前缀),PAPR阈值为信号的平均功率与附加值之和,依据经验取附加值为4.68dB。具体仿真参数如表1所示。
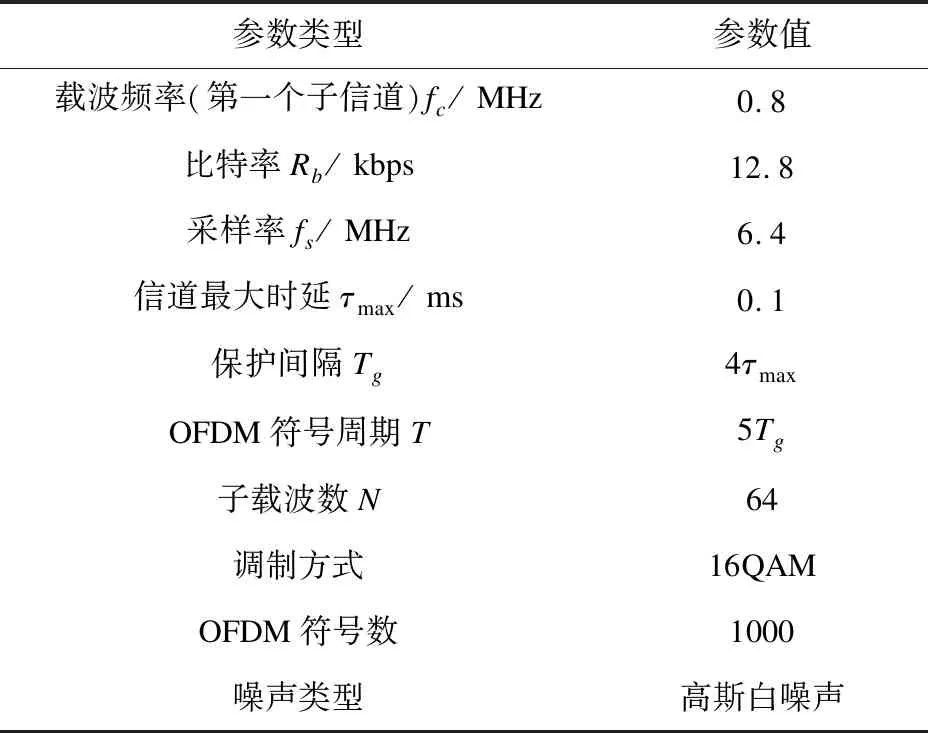
表1 仿真参数表
3.2 仿真流程
DCT-ACE联合优化算法仿真流程如图3所示。数据输入选定,参数配置完成后进行数据的调制映射处理,经串并转换后采用星座映射使得数据的传输速率加快。将此时的频域数据进行DCT矩阵变换,利用IFFT转换到时域,进行限幅处理,判断此时信号幅度是否满足迭代判决条件,若不满足迭代次数及幅度限制要求,利用FFT将信号转为频域进行ACE约束,迭代处理数据;若满足则直接进行数据的输出。
3.3 仿真结果及分析
针对FH-OFDM信号而言,PAPR是指一个符号周期内瞬时功率峰值和信号平均功率之间的比值,所以第k个FH-OFDM符号的PAPR可表示为
0≤k≤N-1
(13)
PAPR抑制效果的直接表现形式是PAPR的概率分布情况,通常用互补累积分布函数(Complementary Cumulative Distribution Function,CCDF)进行表征,其定义为超过某一阈值λ的概率,数学表达式为
P(PAPRk>λ)=1-(1-e-λ2)N
(14)
综上,为验证所提出DCT-ACE联合优化算法的性能,从抑制PAPR效果和误码率(Bit Error Ratio,BER)两个角度将ACE算法、DCT算法与DCT-ACE联合优化算法进行仿真对比。
图4为迭代4次的ACE与DCT-ACE联合优化算法仿真对比结果。
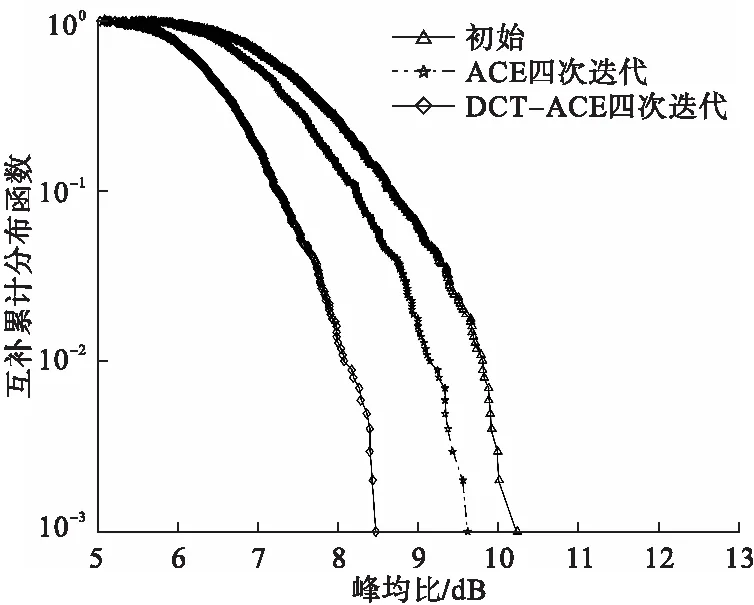
图4 迭代4次的ACE与DCT-ACE联合优化算法
由图4可见,传统ACE算法能够大幅改善系统PAPR较高的问题,但是随着迭代次数增加,运算复杂度也会逐渐加大,同时得到PAPR的收敛速度也会变慢。在DCT-ACE联合优化算法中由于DCT矩阵为正交阵,其计算量可以忽略不计,因此两种算法的复杂程度相当,但DCT-ACE联合优化算法收敛速度明显优于ACE算法。定量上,与原始信号PAPR相比,ACE算法优化了0.6dB,DCT-ACE优化了1.8dB,即DCT-ACE比ACE算法优化了1.2dB,改善了信号的PAPR抑制性能。
图5为DCT与DCT-ACE联合优化算法仿真对比结果。

图5 DCT与DCT-ACE联合优化算法
由图5可知,虽然传统DCT算法利用自身正交性能够改善系统的PAPR,但其收敛较DCT-ACE联合优化算法慢。定量上,与原始信号PAPR相比,DCT算法优化了1.2dB,DCT-ACE联合优化算法优化了1.7dB,即DCT-ACE比DCT算法优化了0.5dB,改善了信号的PAPR抑制性能。
不同算法下的误码率性能曲线如图6所示,将图6在信噪比约为-5.8dB至-5dB范围内曲线进行局部放大后得到图7。
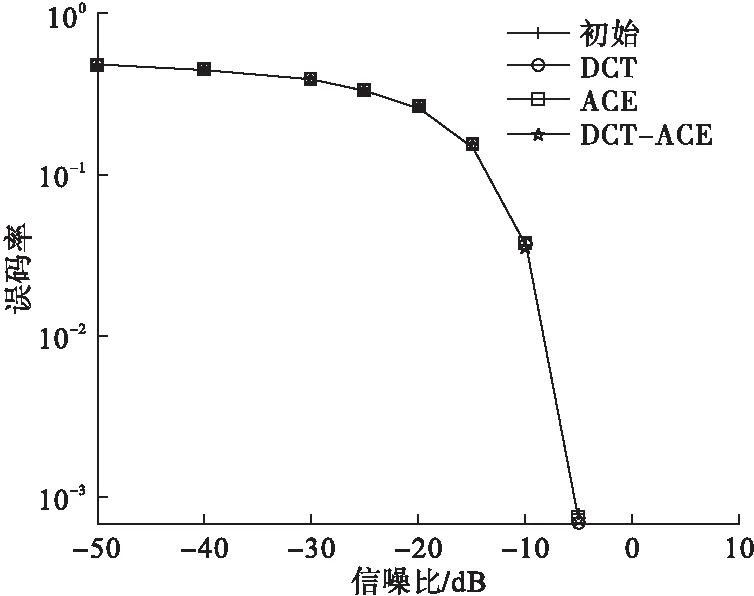
图6 不同算法下的误码率性能曲线

图7 不同算法下的误码率性能曲线细节图
由图7可知,就FH-OFDM信号本身而言,经ACE算法、DCT算法和DCT-ACE联合优化算法抑制PAPR后,信号的抗噪声性能差异不大。当信噪比为-5dB时,未经PAPR抑制算法处理的原FH-OFDM信号对应的误码率为7.7344×10-4;经由DCT算法、ACE算法和DCT-ACE联合优化算法抑制PAPR之后信号的误码率分别为6.7578×10-4、7.4609×10-4和7.1875×10-4。总体而言,DCT-ACE联合优化算法对应的信号误码率低于ACE算法,高于DCT算法。
4 结论
以抑制PAPR为切入点,提出了一种FH-OFDM信号DCT-ACE联合优化抑制PAPR方法,该方法较传统ACE算法和DCT算法的收敛速度快,抑制PAPR效果更好,且抑制PAPR后信号的误码率较低。仿真结果表明,从抑制PAPR效果和误码率两个角度来说,DCT-ACE联合优化算法可适应通信系统的时效性要求,在理论层面上具有一定的意义。
