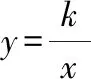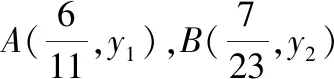浅谈数形结合思想在初中数学教学中的应用
2021-07-06黄莉
黄 莉
(江苏省苏州市吴江区震泽初级中学 江苏 苏州 215000)
在初中数学的教学目标中,培养学生感受数形结合的思想是很重要的,从初一的数轴开始到初三的函数,在这些知识的学习过程中时刻渗透着数形结合的思想方法。我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合千般好,隔离分家万事休。”故而在探索数学问题的过程中,要有意培养学生由数思形,见形思数,并善于应用数形结合的方法来解决数学中的实际问题[1]。
1.在数轴上的应用
数轴是数与图形联系的纽带,在引入负数之后,为了形象的描述一个数,就可以用数轴上的点表示数,在数轴上的数是按照一定顺序排列的,通过数轴上两个数表示的点的位置关系,就可以判断这两个数的大小。在苏教版七年级上册2.3数轴中,例如:利用数轴比较-0.5和-3.5大小,此时可以让学生在数轴上先描出表示-0.5和-3.5这两个负数的点,观察两点的位置,通过在数轴上右边的数总比左边的数大,故而得到-0.5>-3.5,在这里借助数轴让学生初步感受数形结合的思想。
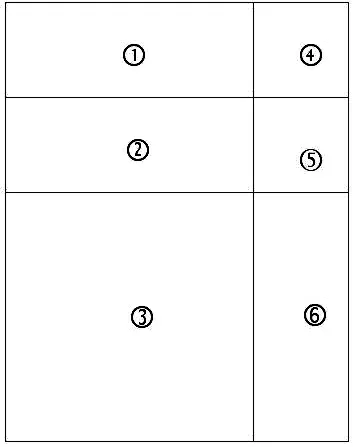
通过数轴可以比较两个具体数的大小,也可以比较两个抽象数的大小,例如:点A、B在数轴上的位置如图1所示,它们分别表示数a、b。将a、b、1、-1四个数按从小到大的顺序排列起来;如将点B向右移动3个单位后,再将a、b、1三个数按从小到大的顺序排列起来.本题中a、b、-1在数轴上如图2直观的可以看到, 通过数-1的位置通过数轴找到其相反数1的位置是本题的关键, 继而得到b<-1< 1 在苏教版七年级上册2.4绝对值与相反数的第一课时中, 通过小明家和小丽家分别在学校的正西方3km和正东方2km, 上学所花的时间与他们家到学校的距离有关的这个实际生活中的问题引入了绝对值的概念, 让学生更容易理解绝对值的意义。实际上为了让学生更好的掌握绝对值, 需让学生理解一个数是由符号和“数值”表示出来的, 其中符号代表的是在原点的左边还是右边, “数值”则是与原点之间的距离, 那么这个距离就是绝对值. 例如: -3.5的符号“-”代表的是在原点的左边, 数值3.5代表的是与原点的距离是3.5, 在数轴上可以很清晰的画出点到原点的距离, 从而让学生明白-3.5的绝对值为3.5。通过数值让学生更容易学会绝对值的应用,充分的体验了数形结合思想在学习中的作用[2],并提升了学生对相关知识的自主探索的能力。 在苏教版七年级下册11.2不等式的解集中,把不等式的解集表示在数轴上,可以让学生直接观察到不等式的解集有无数多个。在苏教版七年级下册11.6一元一次不等式组中,众所周知的一元一次不等式组的解集规律:同大取大, 同小取小, 大小小大取中间, 大大小小是无解[3]。此规律则是通过数轴得来的, 首先要将两个一元一次不等式的解集都表示在同一个数轴上, 通过数轴找到并画出两个一元一次不等式解集的公共部分, 从而得到了一元一次不等式组的解集.在此过程中利用数轴让学生充分掌握一元一次不等式组的解集的表达, 亲身体验数形结合思想在不等式中的应用, 为之后的学习奠定基础。 几何是数学上对“形”研究的一个很重要的方面,因相比数量关系更能形象的展现出来,因此在几何问题上应用数形结合的思想,让学生加深对有关图形的认识,并养成学生保持研究性学习的良好习惯,发展了学生的空间观念,提高学生的逻辑思维能力、分析问题和解决与几何有关问题等能力。 在苏教版七年级下册9.3多项式乘多项式中,例如:计算(a+b)(a+2b)时,可看为计算长是a+b,宽是a+2b的长方形的面积,如下图: 其中①②⑥是长为a,宽为b,面积为ab的长方形,③是面积为a2的正方形,④⑤是面积为b2的正方形,所以①②③④⑤⑥的面积总和为a2+3ab+2b2,即(a+b)(a+2b) =a2+3ab+2b2, 通过利用不同的方法计算同一个图形的面积来引导学生掌握多项式乘多项式的法则, 从形的方面直观的体现出几何美,并加深学生对法则的认识,提高了学生学习的积极性.在苏教版七年级下册9.5因式分解中,用拼图的方式来加深学生对于因式分解的理解,明白最后的结果一定是乘积的形式.例如:因式分解a2+3ab+2b2,可借用上图的矩形,发现矩形的面积可以用(a+b)(a+2b)来表示,即a2+3ab+2b2=(a+b)(a+2b).在这个过程中让学生明白整式乘法和多项式的因式分解的联系。 初中阶段学习的函数包括一次函数,反比例函数,二次函数和锐角三角函数等。函数是揭示了事物的变化规律的一种有效手段,也是研究运动变化的数学模型,通过函数可以表达并探索具体问题的数量关系及变化规律,让学生充分的体会到数量和图形两者之间的联系,更深层次的感受到数形结合的思想[4]。 在苏教版九年级下册5.2二次函数的图像与性质中,要引导学生利用数形结合的方法解决比较函数中的参数大小。例如:二次函数y=(x-a)(x-b)-2(a 在数轴、几何、函数等章节的教学过程中,引导学生要善于利用数形结合的方法去思考问题,并在思想上让学生潜移默化的感受到数形结合的思想,加深学生对数形结合思想在解题时能够让过程更简洁的印象,故而可以更有效的掌握所学的知识,拓宽学生的数学思维,对学生今后的发展有一定的帮助。
2.在几何问题上的应用
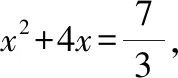
3.在函数上的应用